Improving Student Performance in Developmental Mathematics Courses Wade

Improving Student Performance in Developmental Mathematics Courses Wade Ellis, Jr. West Valley College in Saratoga, California wellis@ti. com

Outline Introduction n Learning Skills (appropriate for a Math course) n Instructional Design n Bloom’s Taxonomy (updated) n Learning Process Methodology n An example of a lesson n Additional Information n Comments and Questions n

Introduction n Basic Skills Initiative (BSI) in California n The Big Five/Social aspects of a course n n n n n Come to class, On time, Pay attention Take notes, and Do your homework Context-base activities High expectations Frequent feedback (My. Math. Lab) What we know about Adult Learners

Adult Learners Malcolm Knowles makes the following assumptions about the design of learning for adult learners [Andragogy] 1. Adults need to know why they need to learn something, 2. Adults need to learn experientially, 3. Adults approach learning as problem-solving, and 4. Adults learn best when the topic is of immediate value.

Introduction (cont’d) n Neuroscience research n Act/Observe-Reflect/Conjecture/Test n (David Kolbe and James n Zull) Emotions make a difference in retention n What students think of themselves n Social persuasion (Albert Bandura)

Introduction (cont’d) n Uri Treisman (specific to mathematics) Adaptive Reasoning n Strategic Competence n Conceptual Understanding n Productive Disposition n Procedural Fluency n

Dos and Don’ts n n n Don’t say “That’s easy. ” when asked to talk about a problem. Do return tests the next class meeting. Don’t answer questions students can answer. Do use lectures to wrap up learning. Don’t lecture the whole period. Don’t use green or red colored chalk or markers. Do acknowledge good thinking. Don’t give partial credit. (Yes, you should. ) Do come to class early. Do train your tutors not to pick-up a pencil. Do ask students to explain or verify.

Learning Skills Learning as a Process that can be improved n Examples of Learning Skills Validating results n Using prior knowledge n Constructing examples n Abstracting n Generalizing n Persisting n Accepting responsibility n

Instruction Design Bloom’s Taxonomy of Learning Information n Knowledge n Application n Problem Solving n Evaluation n Research n - remembering - understanding - applying - analyzing - judging - creating

Bloom’s Taxonomy of Learning Information n Knowledge n Application n Problem Solving n Evaluation n Research n - remembering - understanding - applying - analyzing - judging - creating

Instruction Design Creating Learning Materials n Deciding on the behaviors you want the students to display as a result of the course n Backward design Concept Map (at the beginning of the course) n Creating a Lesson n Seeing the textbook as a resource, but not the course n Infusing a lessons with what we have learned n

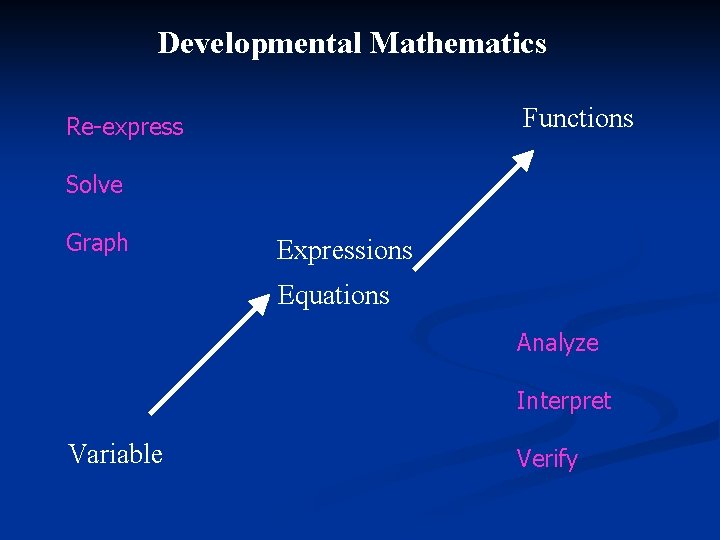
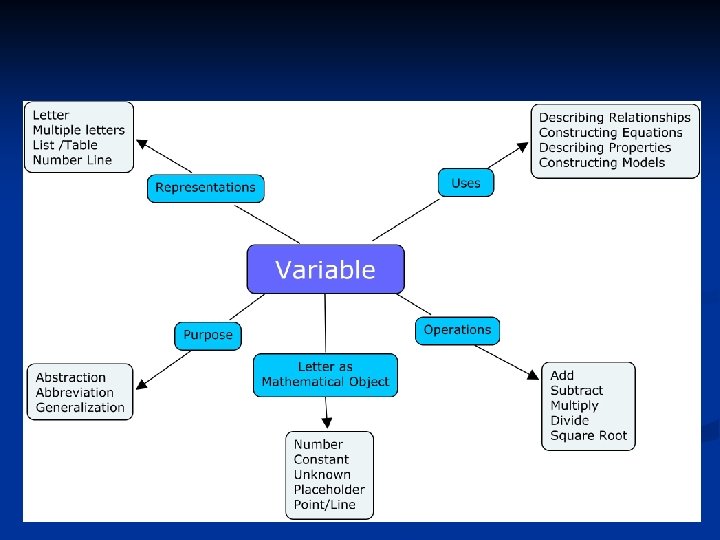
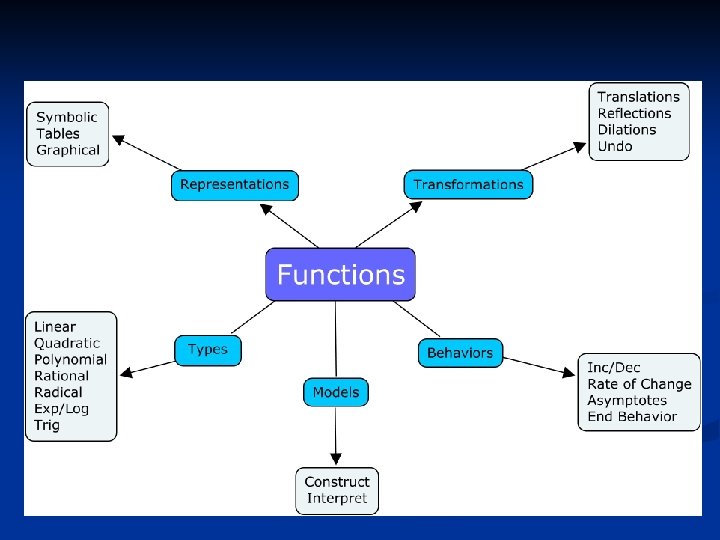
Developmental Mathematics Functions Re-express Solve Graph Expressions Equations Analyze Interpret Variable Verify

Learning Process Methodology 1. 2. 3. Preparation Learning Activity Reflection

1. Preparation Why? n Where does it fit in the knowledge framework? n Prerequisites n Goals n Performance Criteria n Language/Vocabulary n Resources n

2. Learning Activity Plan n Key Questions/Critical Thinking Questions n (Inquiry Questions encouraging Reflection) Examples and Models n Application n Problem Solving n

3. Reflection Self-Assessment n Extension n

The Contour Map n Contour Map

1. Preparation Why? Understanding contour mapping will help you in reading such maps when you deciding on paths for power lines or hiking paths. Where does it fit in the knowledge framework? You can currently read road maps and hiking trail maps. The ability to understand topographic information superimposed on these maps can allow you to understand the placement of buildings or plan hikes more effectively. Prerequisites The ability to read street and road maps. An understanding of the coordinate plane. Goals The ability to interpret topographic maps. The ability to create a simple topographic map from data. Performance Criteria Reading topographic maps. Language/Vocabulary Slicing plane Level curve Contour map Resources Contour map animation

2. Learning Activity Plan 1. Read the Critical Thinking Questions 2. Work with the Contour map program 4. Answer the Critical Thinking Questions 3. Interpret the Applications 4. Solve the Problems Examples and Models Contour Maps (see below) Key Questions/Critical Thinking Questions (Inquiry Questions) Why are the slicing planes the same distance apart? What does it mean when the contour lines are close together on the 2 D contour map? How can you tell which peak is highest from the contour plot? Could the contour plot be of a set of valleys rather than a set of peaks? What does it mean when there is a large region at the top of a peak? Application Another topographic map to interpret (see below) Problem Solving Decide on the steepest ascent to the highest mountain or ridge. Interpret a temperature contour map.

3. Reflection Self-Assessment Can you determine the steepest part of a topographical map? Can you determine the saddle points of a topographical map? Can you determine where the lakes or plains are on a topographical map? Extension To what other measurements can contour maps be applied? Why would such maps be useful?

Comments and Questions wellis@ti. com

Additional Information n Basic Skills as a Foundation for Student Success in California Community Colleges http: //cccbsi. org/publications (choose Literature Review) n Basic Skills Handbook http: //cccbsi. org/publications (choose Basic Skills Handbook) n n n James Zull, ( 2002). The Art of Changing the Brain: Enriching the Practice of Teaching by Exploring the Biology of Learning, . Knowles, M. (1984). Andragogy in Action. San Francisco: Jossey-Bass. Dan Apple, and others (2009). Electronic Faculty Guidebook. Lisle, Illinois: Pacific Crest. http: //www. pcrest. com/PC/FGB/4 th/index. htm n Contour Map