Improving Matching algorithms for IQ switches Abhishek Das

Improving Matching algorithms for IQ switches Abhishek Das John J Kim

Motivation l Results known: 1. 2. 3. With speedup 2, OQ switch can be emulated [Shang-Tse Chuang et al] Maximum Weight Matching (MWM) provides 100% throughput [Mc. Keown et al] With speedup 2, any maximal matching can achieve 100% throughput [Dai and Prabhakar] l What about maximal matching algorithms with weights within a factor of k of MWM (kapproximation)? l Is speedup s < 2 sufficient to guarantee stability?

Fluid model equations for switch l 1. 2. 3. l Queue-lengths represented by ij(t) = ij(0) + Aij(t) - Dij(t) 0 ij (t) = ij(t) - Dij (t) = ijm 1{ ij(t)>0} for any admissible load matrix , , (t) W* (using Birkhoff-von Neumann decomposition), where W* is the weight of Maximum Weight Matching

K-approximation to MWM l l l Lyapunov function L(t) = (t), (t) L (t) = 2 (t), (t) = 2[ (t), (t) - D (t), (t) ] 2[W* - D (t), (t) ] Using speedup s, D (t), (t) = s. ijm , (t) L (t) 2[W* - s. ijm , (t) ] = 2[W* - s. w] (w is weight of the matching) 0 if W* s. w Now for a k-approximation matching algorithm, k. w W* If k s, we satisfy W* k. w s. w and achieve 100% throughput.

K-approximation to MWM (contd. ) l Greedy i. LQF is 2 -approximation – l l l requires speedup s >= 2 (but so does any maximal matching) Any other k-approximation to weighted matching? Weighted matching algorithms use min-cost max-flow algorithms Futile attempts at coming up with other Lyapunov functions – Cij(n) = Xi(n) + Yj(n) - ij(n) where Xi(n) = j ij (n) and Yj(n) = i i j(n)

Why look at VOQ sizes? l l Disappointed souls looking at the bigger picture!! Weights are bad for hardware complexity – l l Requires multi-bit integer comparators LPF is already stable without speedup LPF vs LQF(MWM) – Ratio of matching weights vary from 1 (~70% load) to 20 (90% load)

Matching size with speedup s l Maximum size matching is not stable – l l l Requires speedup? L(t) = (t), 1 L (t) = (t), 1 - D (t), 1 N because i ij 1 and j ij 1 D (t), 1 ijm , 1 since D ij (t) = ijm 1{ ij(t)>0} L (t) N - i |Mi | – – speedup s: s matchings |M| is the size of the matching 0 if i |Mi | N, thus achieving 100% throughput. – Note that its total load ( (t), 1 ) and not N

K-approximation vs Heuristics l Many approximate matching algorithms known (linear and poly-logarithmic) l Approximate matching algorithms compare to the maximum size matching (not to the load) l Heuristics to improve the matching size of practical iterative matching algorithms – speedup

Holi-PIM (or HIM) l Attempt to improve upon PIM by generating bigger size matching in each iteration l Observation: poor matching occurs in PIM when inputs receive multiple grants l Increase the size of matching by considering the number of requests from each input – l equivalent to considering the number of HOL packets or the “fanout” from each input Similar to lonely output allocator (Interconnection Networks – Dally&Towles)

HIM implementation l Requires log(N) control bits from each input l Weights are assigned based on the fanout of each input l How to break ties – – l Randomly Round-robin manner Weighted probability vs strict weights

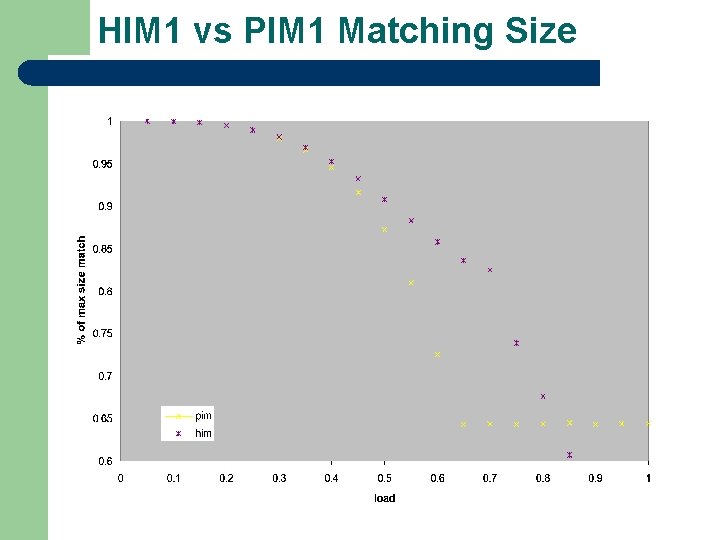
HIM 1 vs PIM 1 Matching Size

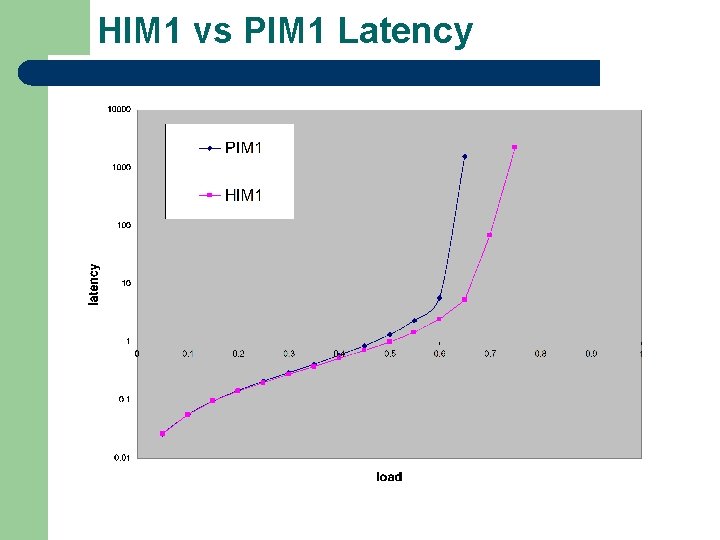
HIM 1 vs PIM 1 Latency

Problems with HIM l HIM performs better than PIM but still does not give 100% throughput l Fairness issue: HIM is not a fair algorithm as it will favor the shorter queues l i. SLIP 1 is known to give 100% throughput on uniform traffic and has simple hardware complexity l Can i. SLIP take advantage of the HIM weights?

i. SLIP+HIM l l Add the HIM weights to i. SLIP The weight of each edge of the request is determined by combining the i. SLIP weights (priority pointers) and the HIM weights l At intermediate loads, HIM weight should improve the performance l At high load, the HIM weights should be identical and i. SLIP should dominate

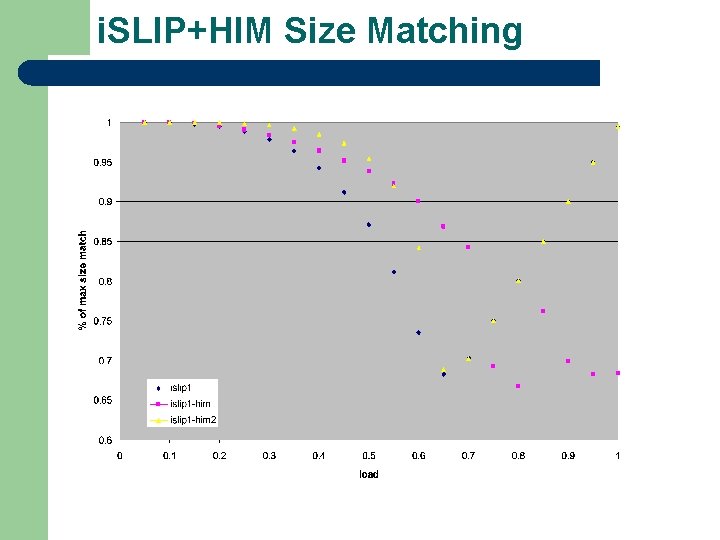
i. SLIP+HIM Size Matching

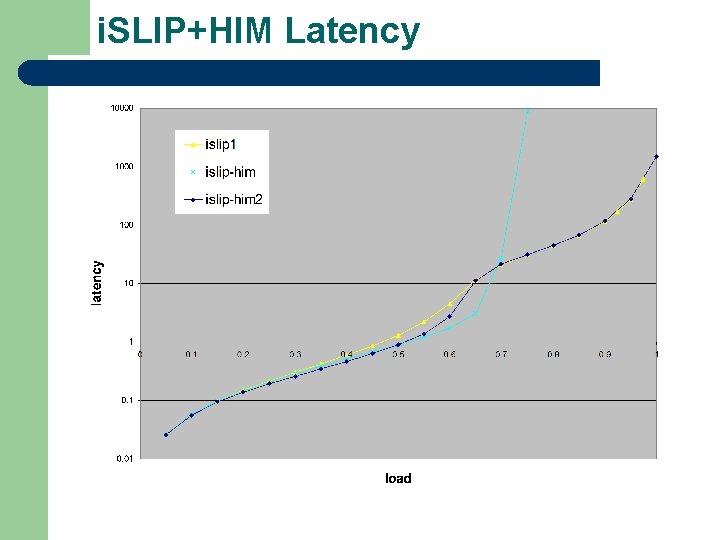
i. SLIP+HIM Latency

Non-uniform Traffic l i. SLIP is known to behave poorly on nonuniform traffic pattern l HIM does not significantly improve on nonuniform as it is an attempt of maximum size matching, not maximum weight

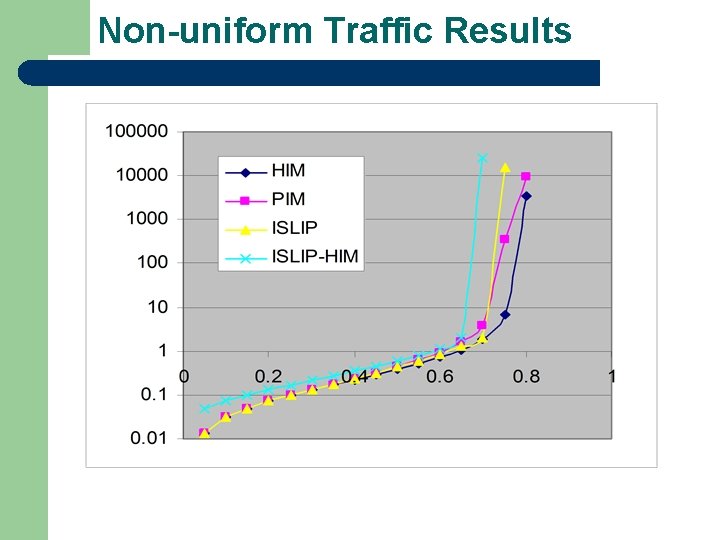
Non-uniform Traffic Results

Future Improvements l Incorporate weights into HIM – Have predetermined threshold on the size of the VOQ and use them as priorities

Conclusions l Showed required stability conditions for matching algorithms (with and without weight) l Introduced and studied a new practical iterative matching algorithm: Holi-PIM under unform traffic