Improving Locality through Loop Transformations COMP 512 Rice

Improving Locality through Loop Transformations COMP 512 Rice University Houston, Texas Fall 2003 Copyright 2003, Keith D. Cooper & Linda Torczon, all rights reserved. Students enrolled in Comp 512 at Rice University have explicit permission to make copies of these materials for their personal use. COMP 512, Fall 2003 1

The Opportunities • Compilers have always focused on loops Higher execution counts > Repeated, related operations > • Much of real work takes place in loops Remember Fortran H (linear algebra) Several effects to attack • Overhead > Decrease control-structure cost per iteration • Locality Spatial locality use of co-resident data > Temporal locality reuse of same data > • Parallelism > ||’ism Move loop w/independent iterations to inner (outer) position COMP 512, Fall 2003 *2

Eliminating Overhead Loop unrolling (the oldest trick in the book) • To reduce overhead, replicate the loop body do i = 1 to 100 by 1 a(i) = a(i) + b(i) end becomes (unroll by 4) Sources of Improvement do i = 1 to 100 by 4 a(i) = a(i) + b(i) a(i+1) = a(i+1) + b(i+1) a(i+2) = a(i+2) + b(i+2) a(i+3) = a(i+3) + b(i+3) end • Less overhead per useful operation • Longer basic blocks for local optimization COMP 512, Fall 2003 3

Eliminating Overhead Loop unrolling with unknown bounds • Generate guard loops do i = 1 to n by 1 a(i) = a(i) + b(i) end becomes (unroll by 4) • While loop needs an explicit update • Used in this form in the BLAS & in Bit. Blt COMP 512, Fall 2003 i=1 do while (i+3 < n) a(i) = a(i) + b(i) a(i+1) = a(i+1) + b(i+1) a(i+2) = a(i+2) + b(i+2) a(i+3) = a(i+3) + b(i+3) i=i+4 end do while (i < n) a(i) = a(i) + b(i) i =i+1 end 4

Eliminating Overhead One other use for loop unrolling • Eliminate copies at the end of a loop t 1 = b(0) do i = 1 to 100 t 2 = b(i) a(i) = a(i) + t 1 + t 2 t 1 = t 2 end becomes (unroll + rename) t 1 = b(0) do i = 1 to 100 by 2 t 2 = b(i) a(i) = a(i) + t 1 + t 2 t 1 = b(i+1) a(i+1) = a(i+1) + t 2 + t 1 end More complex cases • Multiple cross-iteration copy cycles use LCM of cycle lengths • Result has been rediscovered many times [Ken’s thesis] COMP 512, Fall 2003 5

Eliminating Overhead Loop unswitching • Hoist invariant control-flow out of loop nest • Replicate the loop & specialize it • • • if (expression) then do i = 1 to 100 becomes a(i) = a(i) + b(i) a(i) = a(i) + (unswitch) if (expression) b(i) then d(i) = 0 end else do i = 1 to 100 No tests, branches in loop body a(i) = a(i) + b(i) Longer segments of straight-line code end Does this happen in real code? If so, its worth doing COMP 512, Fall 2003 See also: Cytron, Lowry, & Zadeck in 13 th POPL (1986) *6

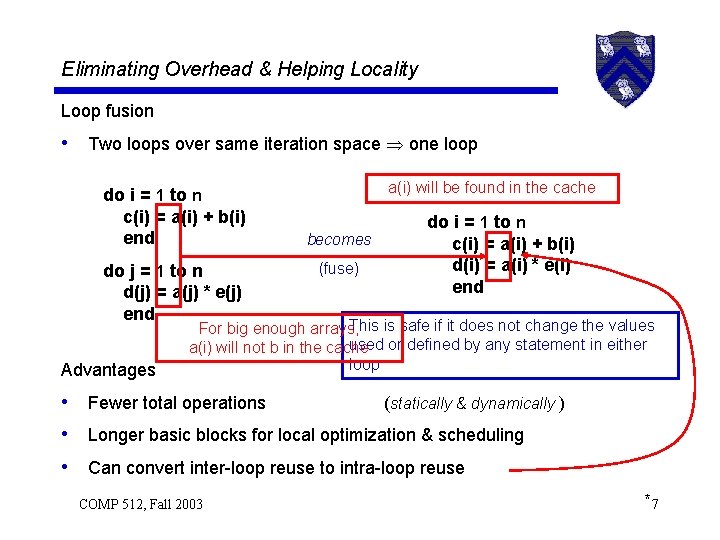
Eliminating Overhead & Helping Locality Loop fusion • Two loops over same iteration space one loop do i = 1 to n c(i) = a(i) + b(i) end do j = 1 to n d(j) = a(j) * e(j) end Advantages a(i) will be found in the cache becomes (fuse) do i = 1 to n c(i) = a(i) + b(i) d(i) = a(i) * e(i) end This is safe if it does not change the values For big enough arrays, used or defined by any statement in either a(i) will not b in the cache loop • Fewer total operations (statically & dynamically ) • Longer basic blocks for local optimization & scheduling • Can convert inter-loop reuse to intra-loop reuse COMP 512, Fall 2003 *7

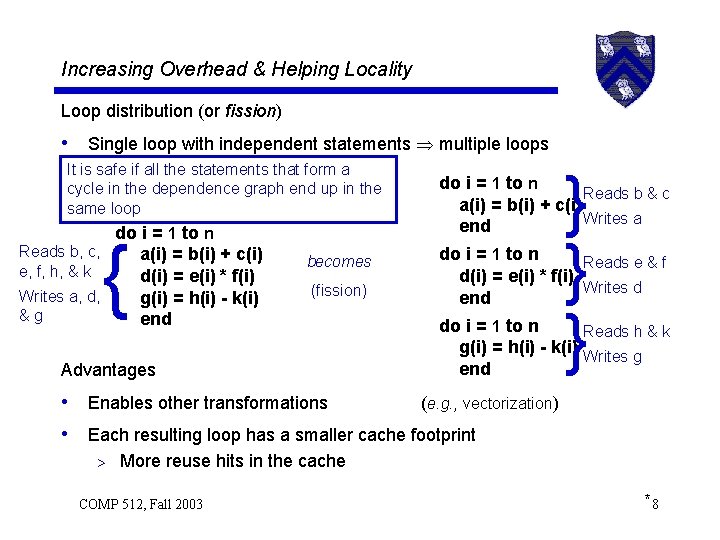
Increasing Overhead & Helping Locality Loop distribution (or fission) • Single loop with independent statements multiple loops It is safe if all the statements that form a cycle in the dependence graph end up in the same loop do i = 1 to n Reads b, c, a(i) = b(i) + c(i) e, f, h, & k d(i) = e(i) * f(i) Writes a, d, g(i) = h(i) - k(i) &g end { becomes (fission) Advantages } } } do i = 1 to n Reads b & c a(i) = b(i) + c(i) Writes a end do i = 1 to n Reads e & f d(i) = e(i) * f(i) Writes d end do i = 1 to n Reads h & k g(i) = h(i) - k(i) Writes g end • Enables other transformations (e. g. , vectorization) • Each resulting loop has a smaller cache footprint > More reuse hits in the cache COMP 512, Fall 2003 *8

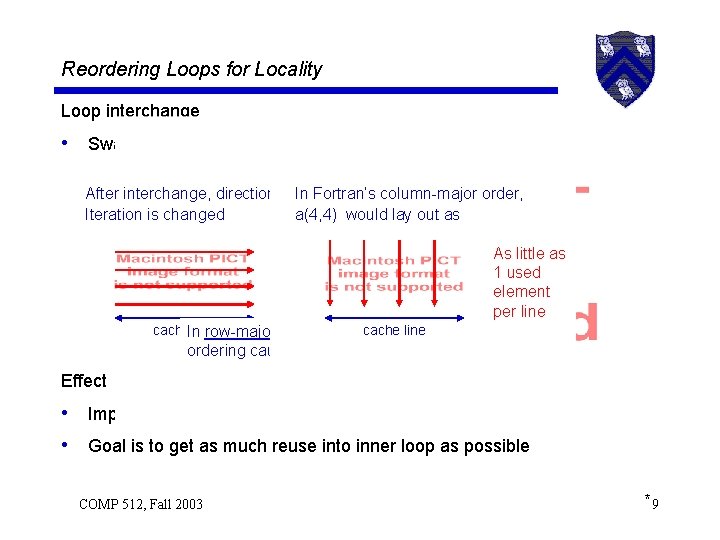
Reordering Loops for Locality Loop interchange • Swap inner & outer loops to rearrange iteration space After interchange, direction of In Fortran’s column-major order, do i = 1 to 50 do j = 1 to 100 Iteration is changed a(4, 4) would lay out as do j = 1 to 100 do i = 1 to 50 becomes a(i, j) = b(i, j) * c(i, j) As little as (interchange) end Runs down 1 used end cache line element per line cache. Inline cache line row-major order, the opposite loop ordering causes the same effects Effect • Improves reuse by using more elements per cache line • Goal is to get as much reuse into inner loop as possible COMP 512, Fall 2003 *9

Reordering Loops for Locality Loop permutation • Interchange is degenerate case > Two perfectly nested loops • More general problem is called permutation Safety • Permutation is safe iff no data dependences are reversed > The flow of data from definitions to uses is preserved Effects • Change order of access & order of computation • Move accesses closer in time increase temporal locality • Move computations farther apart cover pipeline latencies COMP 512, Fall 2003 10

Reordering Loops for Locality Strip mining • Splits a loop into two loops do j = 1 to 100 do i = 1 to 50 a(i, j) = b(i, j) * c(i, j) end becomes (strip mine) This is always safe do j = 1 to 100 do ii = 1 to 50 by 8 do i = ii to min(ii+7, 50) a(i, j) = b(i, j) * c(i, j) end end Effects • Used to match loop bounds to vector length • Used as prelude to loop permutation COMP 512, Fall 2003 (may slow down the code) (for tiling) 11

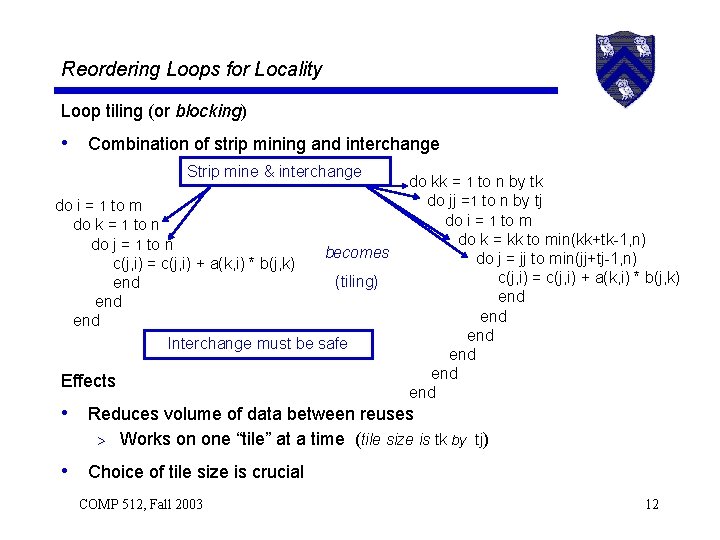
Reordering Loops for Locality Loop tiling (or blocking) • Combination of strip mining and interchange Strip mine & interchange do i = 1 to m do k = 1 to n do j = 1 to n becomes c(j, i) = c(j, i) + a(k, i) * b(j, k) (tiling) end end Interchange must be safe Effects do kk = 1 to n by tk do jj =1 to n by tj do i = 1 to m do k = kk to min(kk+tk-1, n) do j = jj to min(jj+tj-1, n) c(j, i) = c(j, i) + a(k, i) * b(j, k) end end end • Reduces volume of data between reuses > Works on one “tile” at a time (tile size is tk by tj) • Choice of tile size is crucial COMP 512, Fall 2003 12

Rewriting Loops for Better Register Allocation Scalar Replacement • Allocators never keep c(i) in a register • We can trick the allocator by rewriting the references The plan • • Locate patterns of consistent reuse Make loads and stores use temporary scalar variable Replace references with temporary’s name May need copies at end of loop to keep reused values straight > If reuse spans more than one iteration, need to “pipeline” it COMP 512, Fall 2003 13

Rewriting Loops for Better Register Allocation Scalar Replacement do i = 1 to n do j = 1 to n a(i) = a(i) + b(j) end Effects becomes (scalar replacement) do i = 1 to n t = a(i) do j = 1 to n t = t + b(j) end a(i) = t end Almost any register allocator can get t into a register • Decreases number of loads and stores • Keeps reused values in names that can be allocated to registers • In essence, this exposes the reuse of a(i) to subsequent passes COMP 512, Fall 2003 14

Balancing Memory Bound Loops Balance is the ratio of memory accesses to flops • Machine balance is M = • Loop balance is L = accesses/cycle flops/cycle accesses/iteration flops/iteration Loops run better if they are balanced or compute bound • If L > M , the loop is memory bound • If L = M , the loop is balanced • If L < M , the loop is compute bound Making memory bound loops into balanced or compute-bound loops • Need more reuse to decrease number of accesses • Combine scalar replacement, unrolling, and fusion COMP 512, Fall 2003 15

Rewriting Loops for Better Register Allocation Example of Loop Balance do i = 1 to n do j = 1 to n a(i) = a(i) + b(j) end do i = 1 to n t = a(i) do j = 1 to n t = t + b(j) end a(i) = t end Original loop nest After scalar replacement L = 3 accesses/iteration 1 flop/iteration L = 1 access/iteration 1 flop/iteration As memory accesses cost more, this gets better ! COMP 512, Fall 2003 16

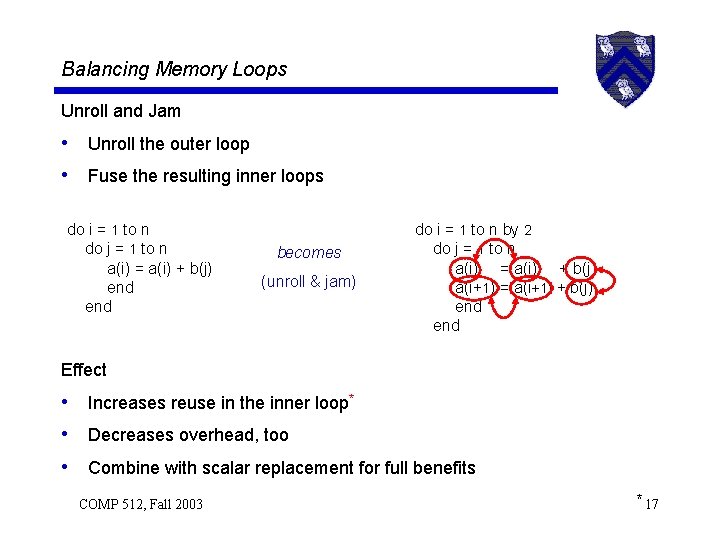
Balancing Memory Loops Unroll and Jam • Unroll the outer loop • Fuse the resulting inner loops do i = 1 to n do j = 1 to n a(i) = a(i) + b(j) end becomes (unroll & jam) do i = 1 to n by 2 do j = 1 to n a(i) = a(i) + b(j) a(i+1) = a(i+1) + b(j) end Effect • Increases reuse in the inner loop* • Decreases overhead, too • Combine with scalar replacement for full benefits COMP 512, Fall 2003 * 17

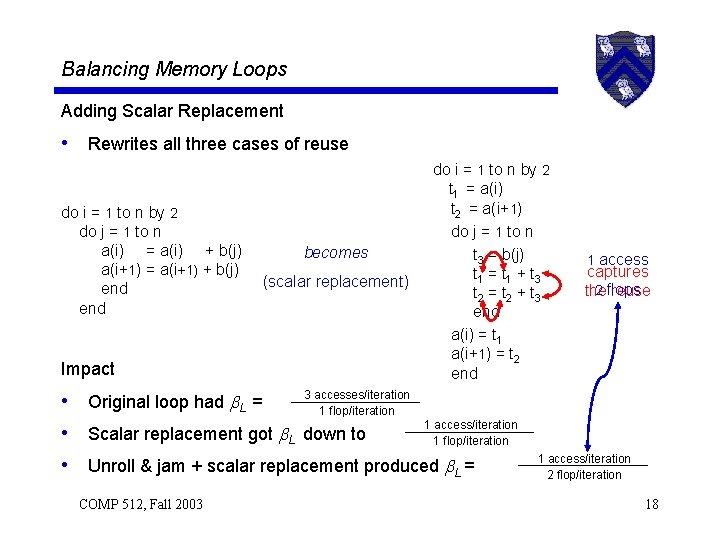
Balancing Memory Loops Adding Scalar Replacement • Rewrites all three cases of reuse do i = 1 to n by 2 do j = 1 to n a(i) = a(i) + b(j) a(i+1) = a(i+1) + b(j) end Impact becomes (scalar replacement) do i = 1 to n by 2 t 1 = a(i) t 2 = a(i+1) do j = 1 to n t 3 = b(j) t 1 = t 1 + t 3 t 2 = t 2 + t 3 end a(i) = t 1 a(i+1) = t 2 end 3 accesses/iteration • Original loop had L = 1 flop/iteration 1 access/iteration • Scalar replacement got L down to 1 flop/iteration • Unroll & jam + scalar replacement produced L = COMP 512, Fall 2003 1 access captures 2 flops the reuse 1 access/iteration 2 flop/iteration 18

Balancing Memory Loops The Big Picture • Scalar replacement + unroll & jam helps • Factors of 2 to 6 for matrix multiply (matrix 300) What does it take to do this in a real compiler? • Data dependence analysis (see COMP 515) • Method to discover consistent reuse patterns (see Carr) • Way to choose the unroll amount Constrained by available registers > Need heuristics to predict allocator’s behavior > COMP 512, Fall 2003 19