Improving Lamport Onetime Signature Scheme MingHsin Chang YiShiung

Outline • • • Introduction Lamport’s Scheme Proposed Scheme Security & Performance Analysis Conclusion

Introduction • One-time signature scheme – is used to sign at most one message;

Lamport’s Scheme • Lamport’s one-time signature scheme is comprised of 3 phases: – Key

Key Generation Phase 1. Select 2 k elements randomly with 1 ≤ i ≤

Signing Phase 1. To sign a k-bit message m = m 1…mk, sig(m) =

Verification Phase 1. To verify the signature check if holds, where 1≤ i ≤

Proposed Scheme • Key Generation 1. Select a number e and set. 2. Derive

Proposed Scheme • To sign a message m: 1. Convert m to base v

Proposed Scheme • To sign a message m, first select a value e, say

Proposed Scheme • Verification 1. To verify the signature, simply check if the signature

Performance Analysis # of public Avg. # of key items signature terms verification Lamport’s

Security Analysis • Security equals to the number of signature terms, in Lamport case,

Conclusion • Although the proposed scheme’s performance is twice as fast as Lamport’s, its

Slides: 15

Download presentation

Improving Lamport One-time Signature Scheme Ming-Hsin Chang, Yi-Shiung Yeh, Elsevier, Appl. Math. Comput. , 2005 Presented by 盧奕吉

Outline • • • Introduction Lamport’s Scheme Proposed Scheme Security & Performance Analysis Conclusion

Introduction • One-time signature scheme – is used to sign at most one message; otherwise the signature can be forged. – has the property of efficient signature generation and verification. – requires a large amount of storage space.

Lamport’s Scheme • Lamport’s one-time signature scheme is comprised of 3 phases: – Key generation phase – Signing phase – Verification phase

Key Generation Phase 1. Select 2 k elements randomly with 1 ≤ i ≤ k and j = 0, 1. (k is the length of the message in base 2). 2. Compute for all i, j.

Signing Phase 1. To sign a k-bit message m = m 1…mk, sig(m) = sig(m 1…mk) = ( ). – i. e. , to sign a message m = 10… 1, the signature becomes:

Verification Phase 1. To verify the signature check if holds, where 1≤ i ≤ k.

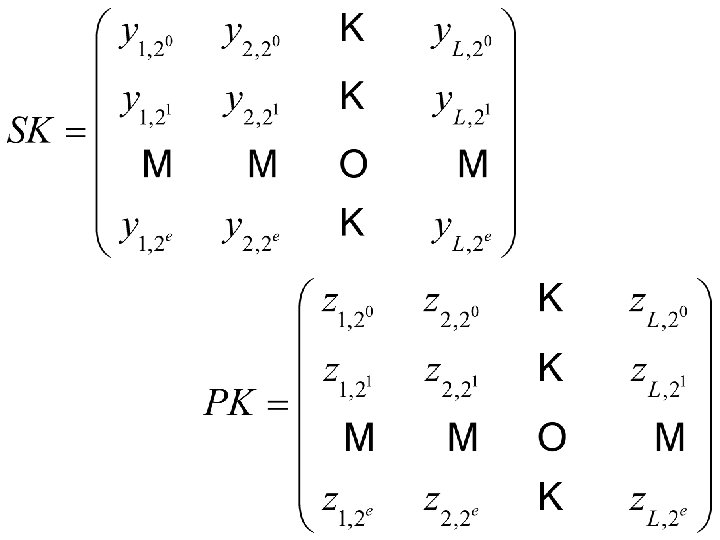
Proposed Scheme • Key Generation 1. Select a number e and set. 2. Derive the value L, which is the length of the message in base v. 3. For each column i, randomly select e+1 elements, where 1 ≤ i ≤ L.

Proposed Scheme • To sign a message m: 1. Convert m to base v representation. 2. For each digit of mi, further convert it to base 2 representation. 3. sig(m) = sig(m 1…m. L) = where , such that the symbol x signifies the 2’s representation of mi.

Proposed Scheme • To sign a message m, first select a value e, say 3, and set v = 2(e+1) = 16. Then convert m to base v, e. g. , m = (3 A… 1)16. Again convert each digit to base 2 representation, i. e. , 3 = (0011)2, A = (1010)2 and 1 = (0001)2, etc.

Proposed Scheme • Verification 1. To verify the signature, simply check if the signature matches the corresponding z’s. If so, the signature is genuine.

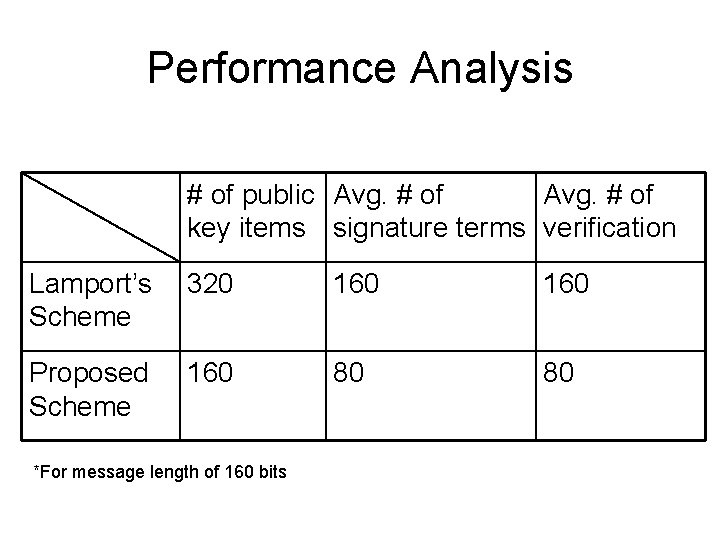
Performance Analysis # of public Avg. # of key items signature terms verification Lamport’s Scheme 320 160 Proposed Scheme 160 80 80 *For message length of 160 bits

Security Analysis • Security equals to the number of signature terms, in Lamport case, it equals to the number of bits. In the proposed scheme, the number of signature terms is halved, L*e/2.

Conclusion • Although the proposed scheme’s performance is twice as fast as Lamport’s, its security, however, is sacrificed. • Due to the particular nature of Lamport’s signature scheme, the performance growth will always be proportional to the security decrease.