Improving Data Mining Utility with Projective Sampling Mark

Improving Data Mining Utility with Projective Sampling Mark Last Department of Information Systems Engineering Ben-Gurion University of the Negev, Beer-Sheva, Israel E-mail: mlast@bgu. ac. il Home Page: http: //www. bgu. ac. il/~mlast/ Mark Last (mlast@bgu. ac. il) 1

Improving Data Mining Utility with Projective Sampling Agenda • Introduction • Learning Curves and Progressive Sampling • The Projective Sampling Strategy • Empirical Results • Conclusions and Future Research Mark Last (mlast@bgu. ac. il) 2

Improving Data Mining Utility with Projective Sampling Motivation: Data is not “born” free • The training data is often scarce and costly • Real-world examples – A limited number of patient records stored by a hospital – Results of a costly engineering experiment – Seasonal records in an agricultural database • Even when the raw data is free, its preparation may still be labor intensive! • Critical question – Should we spend our resources (time and/or money) on acquiring more examples? Mark Last (mlast@bgu. ac. il) 3

Improving Data Mining Utility with Projective Sampling Total Cost of the Classification Process (based on Weiss and Tian, 2008) Training Set Score Set Used to induce the classification model Future examples to be classified by the model • Total Cost = n·Ctr + err(n)·|S|·Cerr + CPU(n)∙Ctime – – – – Ctr - cost of acquiring and labeling each new training example Cerr - cost of each misclassified example from the score set Ctime – cost per one unit of CPU time n – number of training set examples used to induce the model S - the score set of future examples to be classified by the model err (n) – the model error rate measured on the score set CPU(n) – CPU time required to induce the model Mark Last (mlast@bgu. ac. il) 4

Improving Data Mining Utility with Projective Sampling What is this research about? • Problem Statement – Find the best training set size n* that is expected to maximize the overall utility (minimize the Total Cost) • Basic Idea - Projective Sampling – Estimate the optimal training set size using learning and run-time curves projected from a small subset of potentially available data • Research Objectives – Calculate the optimal training set size for a variety of learning curve equations (with and without CPU costs) – Improve the utility of the data mining process using the best fitting curves for a given dataset and an algorithm Mark Last (mlast@bgu. ac. il) 5

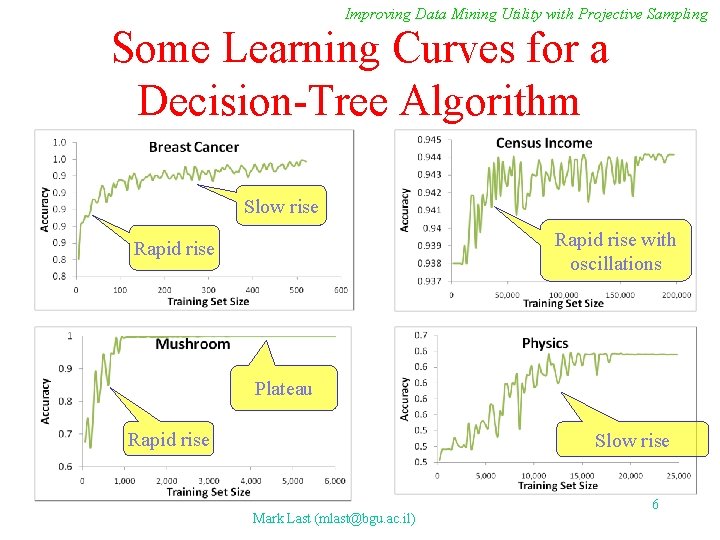
Improving Data Mining Utility with Projective Sampling Some Learning Curves for a Decision-Tree Algorithm Slow rise Rapid rise with oscillations Rapid rise Plateau Rapid rise Slow rise Mark Last (mlast@bgu. ac. il) 6

Improving Data Mining Utility with Projective Sampling The Best Fit for a Learning Curve • Frey and Fisher (1999) – The power law is the best fit for modeling the C 4. 5 error rates • Last (2007) – The power law is the best fit for modeling the error rates of an oblivious decision-tree algorithm (Information Network) • Singh (2005) – The power law is only second best to the logarithmic regression for ID 3, k-Nearest Neighbors, Support Vector Machines, and Artificial Neural Networks Mark Last (mlast@bgu. ac. il) 7

Improving Data Mining Utility with Projective Sampling Progressive Sampling Strategy (Provost et al. , 1999, Weiss and Tian, 2008) • General strategy – Start with some initial amount of training data n 0 – Iteratively increase the training set until there is an increase in total cost • Popular schedules – Uniform (arithmetic) sampling • n 0, n 0+ 2 , … – Geometric Sampling • n 0, a∙n 0, a 2∙n 0, … Mark Last (mlast@bgu. ac. il) 8

Improving Data Mining Utility with Projective Sampling Limitations of Progressive Sampling • Overfitting some local perturbations in the error rate – Progressive sampling costs may exceed the optimal ones by 10%-200% (Weiss and Tian, 2008) • Potential overhead associated with purchasing and pre-processing each sampling increment (especially with uniform sampling). • Our expectation – The projective sampling strategy should reduce data mining costs by estimating the optimal training set size from a small subset of potentially available data Mark Last (mlast@bgu. ac. il) 9

Improving Data Mining Utility with Projective Sampling The Projective Sampling Strategy • Set a fixed sampling increment – Each acquired sample = one data point • Do – Acquire a new data point – Compute Pearson's correlation coefficient for each candidate fitting function (given at least three data points) • Dependent variable: err(n) • Independent variable: training set size n – Find a function with a minimal correlation coefficient Best_Corr • Why minimal • • While ((Best_Corr ≥ 0) and (n < nmax)) Estimate the regression coefficients of the selected function Estimate the optimal training set size n* Induce the classification model M (n*) from n* examples Mark Last (mlast@bgu. ac. il) 10

Improving Data Mining Utility with Projective Sampling Candidate Fitting Functions • Learning Curves – Logarithmic : err. Log (n) = a + b logn – Weiss and Tian: err. WT (n) = a + bn / (n + 1) – Power Law : err. PL (n) = a∙nb – Exponential : err. Exp (n) = abn • Run-time Curves – Linear: CPUL (n) = d n – Power law: CPUPL (n) = c∙nd Mark Last (mlast@bgu. ac. il) 11

Improving Data Mining Utility with Projective Sampling Converting Learning Curves into the Linear Form y = a’ + b’x Function err(n) x y (independent (dependent variable) a (intercept) b (slope) a + b logn err (n) a' b' a + bn / (n + 1) err (n) a' b' a∙nb logn log (err (n)) Exp (a') b' abn n log (err (n)) Exp (a') Exp (b') logn Mark Last (mlast@bgu. ac. il) 12

Improving Data Mining Utility with Projective Sampling Pearson's Correlation Coefficient k – number of data points Mark Last (mlast@bgu. ac. il) 13

Improving Data Mining Utility with Projective Sampling Linear Regression Coefficients y = a + bx • The least squares estimate of the slope: k – number of data points • The least squares estimate of the intercept Mark Last (mlast@bgu. ac. il) 14

Improving Data Mining Utility with Projective Sampling Total Cost Functions • Total Cost. Log (n) = n∙Ctr + d∙n∙Ctime + |S|∙Cerr ∙ (a + b logn) • Total Cost. WT (n) = n∙Ctr + d∙n∙Ctime + |S|∙Cerr ·( a+bn / (n+1)) • Total Cost. PL (n) = n∙Ctr + d∙n∙Ctime + |S|∙Cerr ∙anb • Total Cost. Exp (n) = n∙Ctr + d∙n∙Ctime + |S|∙Cerr ∙abn Mark Last (mlast@bgu. ac. il) 15

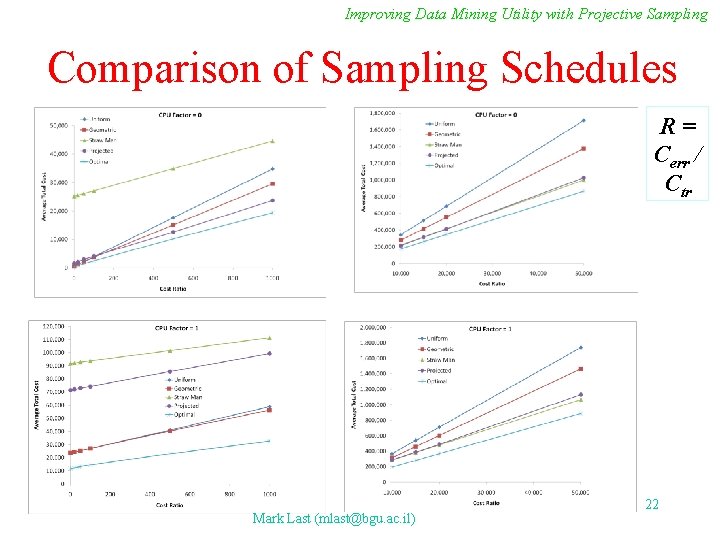
Improving Data Mining Utility with Projective Sampling Optimizing the Training Set Size • Let • R = Cerr / Ctr • Ctr = 1 • CPUL (n) = d n • • Logarithmic: Total Cost. Log (n) = n + d∙n∙Ctime + |S|∙R ∙ (a + b logn) Weiss and Tian: Total Cost. WT (n) = n + d∙n∙Ctime + |S|∙R ∙( a+bn / (n+1)) • • Power Law: Total Cost. PL (n) = n + d∙n∙Ctime + |S|∙R ∙anb Exponential: Total Cost. Exp (n) = n + d∙n∙Ctime + |S|∙R ∙abn Mark Last (mlast@bgu. ac. il) 16

Improving Data Mining Utility with Projective Sampling Experimental Settings • Ten benchmark datasets (see next slide) • Each dataset was randomly partitioned into 25%-50% of test examples and 50%-75% of examples potentially available for training. • The sampling increment was set to 1% of the maximum possible training set size • The error rate of each increment was averaged over 10 random partitions of the training set. • Sampling schedules: Uniform, Geometric (a=2), Straw Man, Projective, Optimal • Cost Ratios (R): 1 – 50, 000 • CPU Factors: 0 and 1 (per one millisecond of CPU time) Mark Last (mlast@bgu. ac. il) 17

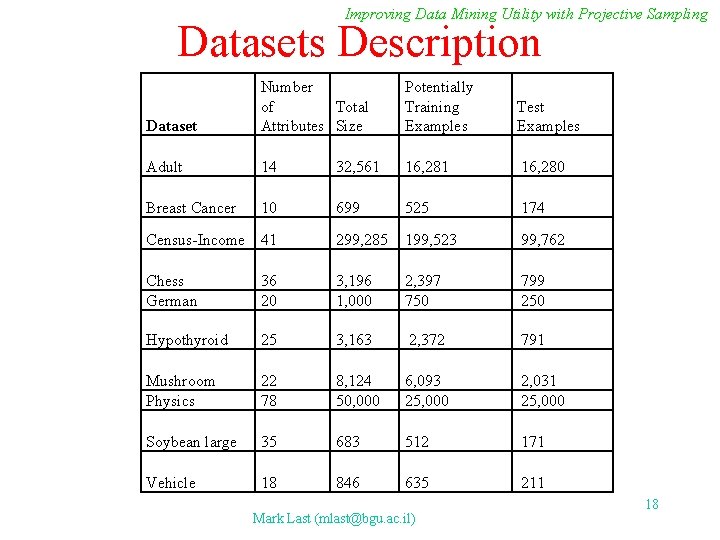
Improving Data Mining Utility with Projective Sampling Datasets Description Dataset Number Total of Attributes Size Potentially Training Examples Test Examples Adult 14 32, 561 16, 280 Breast Cancer 10 699 525 174 Census-Income 41 299, 285 199, 523 99, 762 Chess German 36 20 3, 196 1, 000 2, 397 750 799 250 Hypothyroid 25 3, 163 2, 372 791 Mushroom Physics 22 78 8, 124 50, 000 6, 093 25, 000 2, 031 25, 000 Soybean large 35 683 512 171 Vehicle 18 846 635 211 Mark Last (mlast@bgu. ac. il) 18

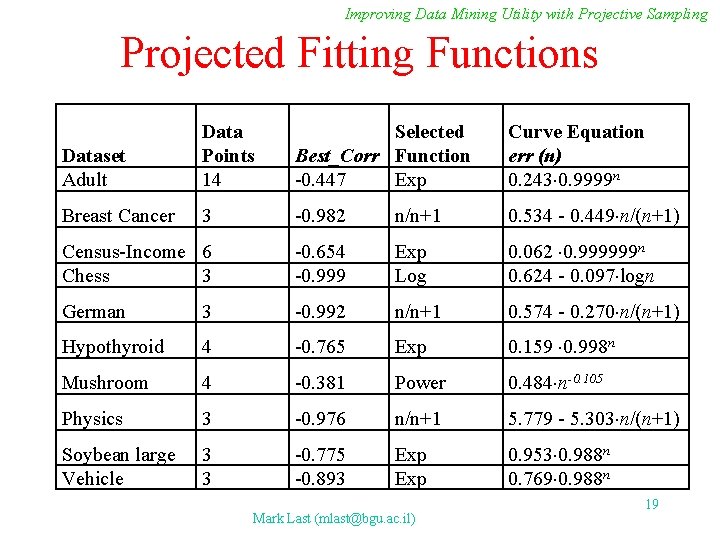
Improving Data Mining Utility with Projective Sampling Projected Fitting Functions Dataset Adult Data Points 14 Selected Best_Corr Function -0. 447 Exp Curve Equation err (n) 0. 243 0. 9999 n Breast Cancer 3 -0. 982 n/n+1 0. 534 - 0. 449 n/(n+1) Census-Income 6 Chess 3 -0. 654 -0. 999 Exp Log 0. 062 0. 999999 n 0. 624 - 0. 097 logn German 3 -0. 992 n/n+1 0. 574 - 0. 270 n/(n+1) Hypothyroid 4 -0. 765 Exp 0. 159 0. 998 n Mushroom 4 -0. 381 Power 0. 484 n-0. 105 Physics 3 -0. 976 n/n+1 5. 779 - 5. 303 n/(n+1) Soybean large Vehicle 3 3 -0. 775 -0. 893 Exp 0. 953 0. 988 n 0. 769 0. 988 n Mark Last (mlast@bgu. ac. il) 19

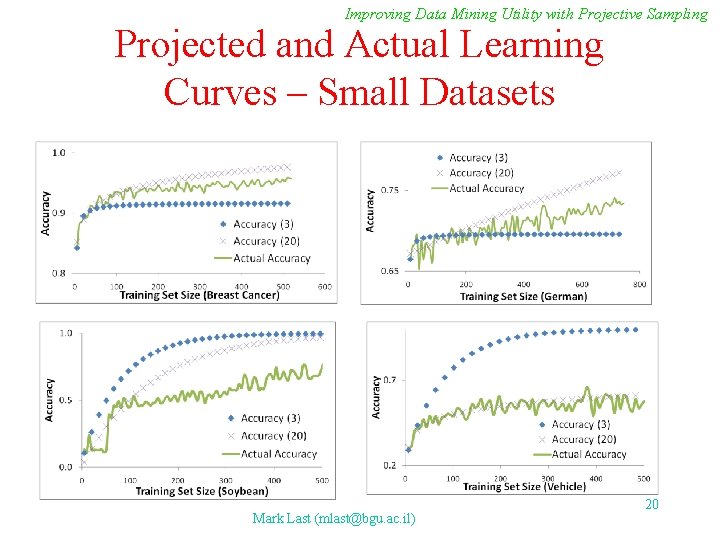
Improving Data Mining Utility with Projective Sampling Projected and Actual Learning Curves – Small Datasets Mark Last (mlast@bgu. ac. il) 20

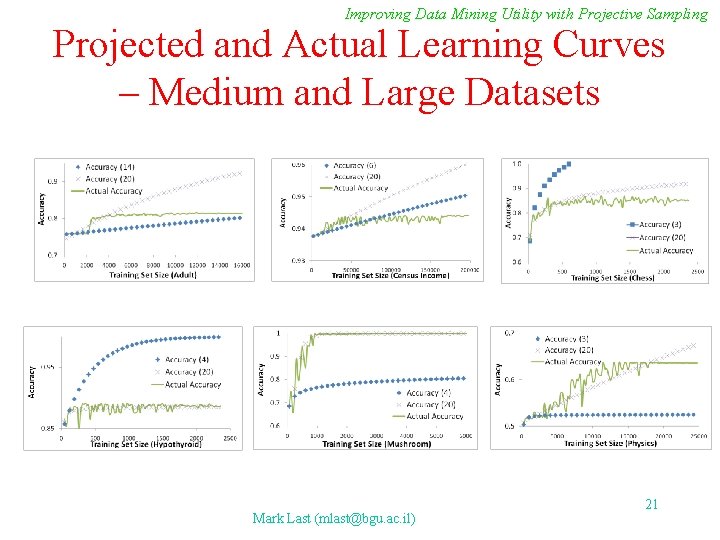
Improving Data Mining Utility with Projective Sampling Projected and Actual Learning Curves – Medium and Large Datasets Mark Last (mlast@bgu. ac. il) 21

Improving Data Mining Utility with Projective Sampling Comparison of Sampling Schedules R= Cerr / Ctr Mark Last (mlast@bgu. ac. il) 22

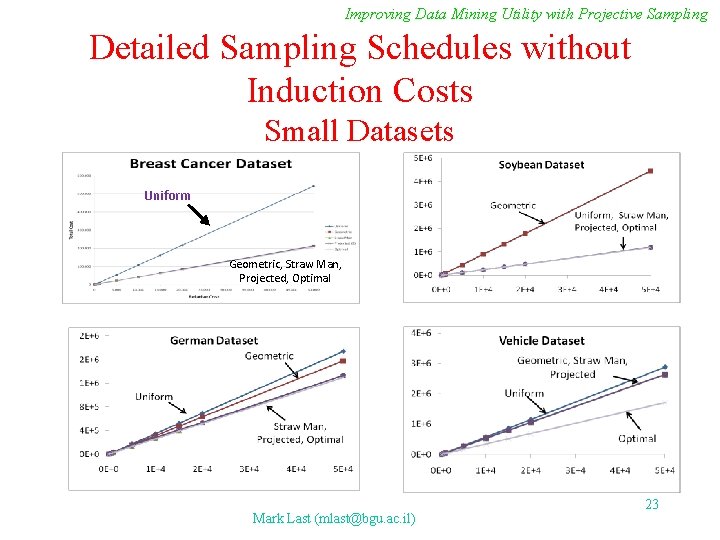
Improving Data Mining Utility with Projective Sampling Detailed Sampling Schedules without Induction Costs Small Datasets Uniform Geometric, Straw Man, Projected, Optimal Mark Last (mlast@bgu. ac. il) 23

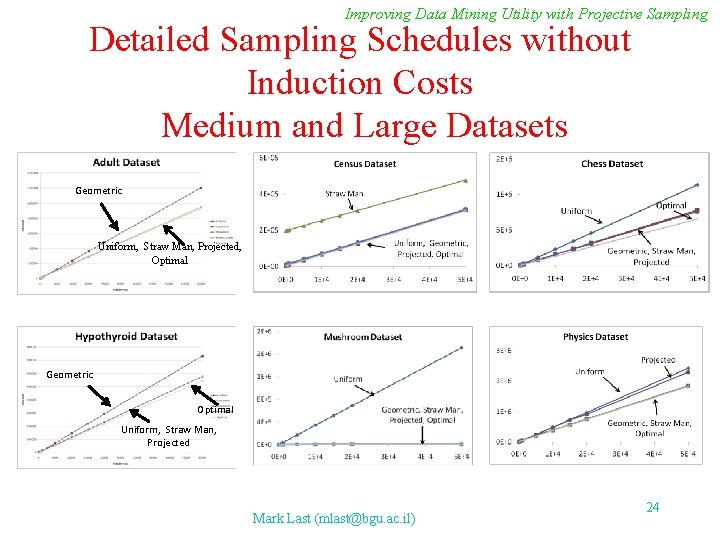
Improving Data Mining Utility with Projective Sampling Detailed Sampling Schedules without Induction Costs Medium and Large Datasets Geometric Uniform, Straw Man, Projected, Optimal Geometric Optimal Uniform, Straw Man, Projected Mark Last (mlast@bgu. ac. il) 24

Improving Data Mining Utility with Projective Sampling Conclusions • The projective sampling strategy estimates the optimal training set size by fitting an analytical function to a partial learning curve • The proposed methodology was evaluated on 10 benchmark datasets of variable size using a decision-tree algorithm. • The results show that under negligible induction costs and high data acquisition costs, the projective sampling outperforms, on average, the alternative, progressive sampling techniques. Mark Last (mlast@bgu. ac. il) 25

Improving Data Mining Utility with Projective Sampling Future Research • Further optimization of projective sampling schedules, especially under substantial CPU costs • Improving utility of cost-sensitive data mining algorithms • Modeling learning curves for nonrandom (“active”) sampling and labeling techniques Mark Last (mlast@bgu. ac. il) 26

Improving Data Mining Utility with Projective Sampling Merci Beaucoup! Mark Last (mlast@bgu. ac. il) 27