Improved Algorithms for Multiplex PCR Primer Set Selection

Improved Algorithms for Multiplex PCR Primer Set Selection with Amplification Length Constraints Kishori M. Konwar Ion I. Mandoiu Alexander C. Russell Alexander A. Shvartsman CS&E Dept. , Univ. of Connecticut APBC 2005 1

Combinatorial Optimization in Bioinformatics • Fast growing number of applications – – – Sequence alignment DNA sequencing Haplotype inference Pathogen identification … High-throughput assay design • • • Microarray probe selection Microarray quality control Universal tag arrays … This talk: Multiplex PCR primer set selection APBC 2005 2

Outline • • • Background and problem formulation “Potential function” greedy algorithm Approximation guarantee Experimental results Conclusions APBC 2005 3

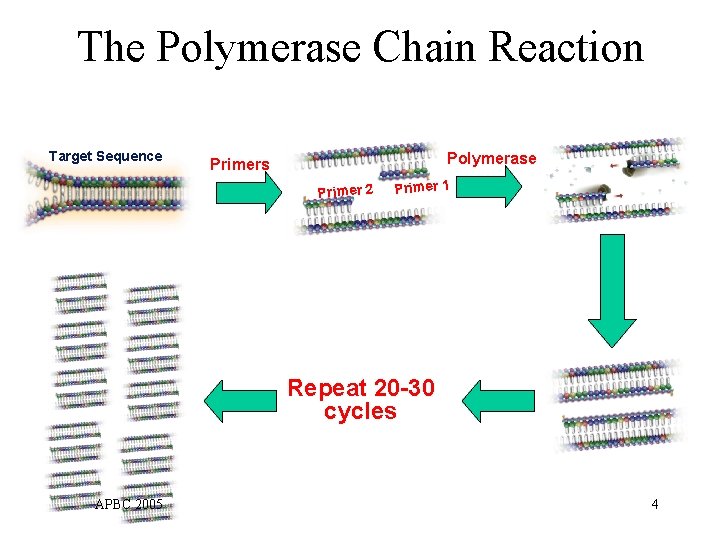
The Polymerase Chain Reaction Target Sequence Polymerase Primers Primer 2 Primer 1 Repeat 20 -30 cycles APBC 2005 4

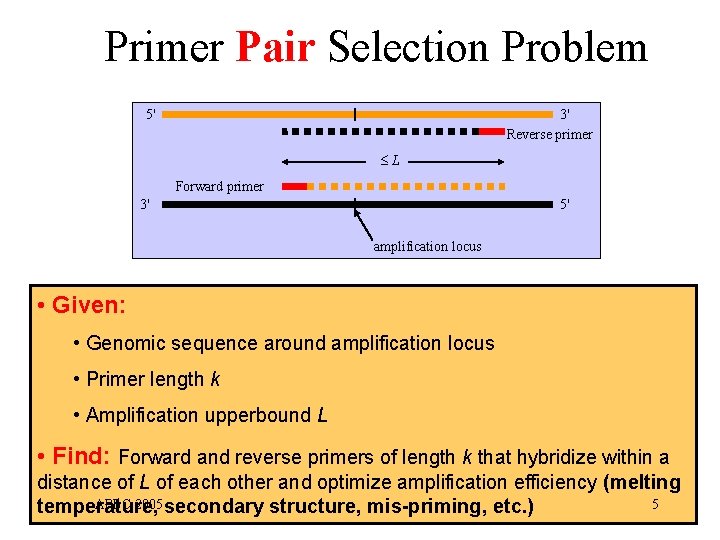
Primer Pair Selection Problem 5' 3' Reverse primer L Forward primer 3' 5' amplification locus • Given: • Genomic sequence around amplification locus • Primer length k • Amplification upperbound L • Find: Forward and reverse primers of length k that hybridize within a distance of L of each other and optimize amplification efficiency (melting APBC 2005 secondary structure, mis-priming, etc. ) 5 temperature,

PCR for SNP Genotyping • Thousands of SNPs to be genotyped using hybridization methods (e. g. , SBE) • Selective PCR amplification needed to improve accuracy of detection steps – whole-genome amplification not appropriate • Simultaneous amplification OK Multiplex PCR APBC 2005 6

Multiplex PCR • How it works – Multiple DNA fragments amplified simultaneously – Each amplified fragment still defined by two primers – A primer may participate in amplification of multiple targets • Primer set selection – Currently done by time-consuming trial and error – An important objective is to minimize number of primers Ø Reduced assay cost Ø Higher effective concentration of primers higher amplification efficiency Ø Reduced unintended amplification APBC 2005 7

Primer Set Selection Problem • Given: • Genomic sequences around n amplification loci • Primer length k • Amplification upper bound L • Find: • Minimum size set S of primers of length k such that, for each amplification locus, there are two primers in S hybridizing with the forward and reverse genomic sequences within a distance of L of each other APBC 2005 8

Previous Work on Primer Selection • • Well-studied problem: [Pearson et al. 96], [Linhart & Shamir’ 02], [Souvenir et al. ’ 03], etc. Almost all problem formulations decouple selection of forward and reverse primers – To enforce bound of L on amplification length, select only primers that hybridize within L/2 bases of desired target – In worst case, this method can increase the number of primers by a factor of O(n) compared to the optimum • [Pearson et al. 96] Greedy set cover algorithm gives O(ln n) approximation factor for the “decoupled” formulation APBC 2005 9

Previous Work (2) • [Fernandes&Skiena’ 02] study primer set selection with uniqueness constraints • Minimum Multi-Colored Subgraph Problem: – Vertices correspond to candidate primers – Edge colored by color i between u and v iff corresponding primers hybridize within a distance of L of each other around i-th amplification locus – Goal is to find minimum size set of vertices inducing edges of all colors APBC 2005 10

The Set Cover Problem m Given: - m Universal set U with n elements Family of sets (Sx, x X) covering all elements of U Find: - Minimum size subset X’ of X s. t. (Sx, x X’) covers all elements of U APBC 2005 11

Selection w/ Length Constraints • “Simultaneous set covering” problem: - Ground set partitioned into n disjoint sets Si (one for each target), each with 2 L elements - Goal is to select minimum number of sets == primers covering at least 1/2 of the elements in each partition SNPi L APBC 2005 L 12

Greedy Setcover Algorithm m Greedy Algorithm: - Repeatedly pick the set with most uncovered elements m Classical result (Johnson’ 74, Lovasz’ 75, Chvatal’ 79): the greedy setcover algorithm has an approximation factor of H(n)=1+1/2+1/3+…+1/n < 1+ln(n) - The approximation factor is tight Cannot be approximated within a factor of (1 - )ln(n) unless NP=DTIME(nloglog(n)) APBC 2005 13

• Set cover Potential Functions • = #uncovered elements • Initially, = n • For feasible solutions, = 0 • Primer selection with length constraints • = minimum number of elements that must be covered = i max{0, L - #uncovered elements in Si} • Initially, = n. L • For feasible solutions, = 0 APBC 2005 14

General setting m m m m Potential function (X’) 0 ({}) = max (X’) = 0 for all feasible solutions X’’ X’ (X’’) (X’) If (X’)>0, then there exists x s. t. (X’+x) < (X’) X’’ X’ ∆(x, X’) for every x, where ∆(x, X’) : = (X’) - (X’+x) Objective: find minimum size set X’ with (X’)=0 APBC 2005 15

Generic Greedy Algorithm m X’ {} m While (X’) > 0 Find x with maximum ∆(x, X’) X’ + x • Theorem: The generic greedy algorithm has an approximation factor of 1+ln ∆max • Corollary: 1+ln(n. L) approximation for PCR primer selection APBC 2005 16

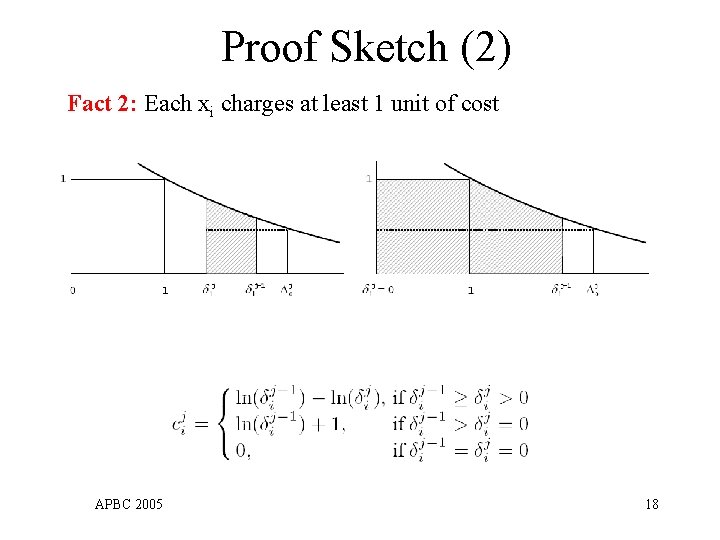
Proof Sketch (1) • x 1, x 2, …, xg be the elements selected by greedy, in the order in which they are chosen • x*1, x*2, …, x*k be the elements of an optimum solution. Charging scheme: xi charges to x*j a cost of where ij = ∆(xi, {x 1, …, xi-1} {x*1, …, x*j}) Fact 1: Each x*j gets charged a total cost of at most 1+ln ∆max APBC 2005 17

Proof Sketch (2) Fact 2: Each xi charges at least 1 unit of cost APBC 2005 18

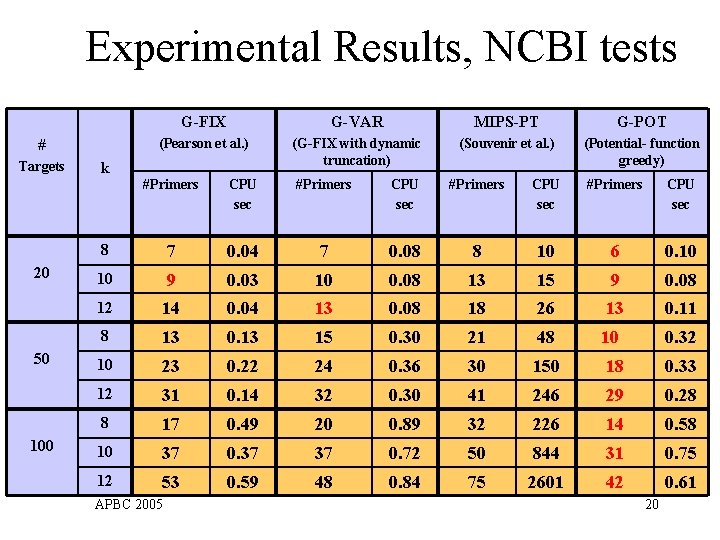
Experimental Setting • • • Datasets extracted from NCBI databases, L=1000 Dell Power. Edge 2. 8 GHz Xeon Compared algorithms – G-FIX: greedy primer cover algorithm [Pearson et al. ] – MIPS-PT: iterative beam-search heuristic [Souvenir et al. ] • Restrict primers to L/2 bases around amplification locus – G-VAR: naïve modification of G-FIX • First selected primer can be up to L bases away • Opposite sequence truncated after selecting first primer – G-POT: potential function driven greedy algorithm APBC 2005 19

Experimental Results, NCBI tests # Targets 20 50 100 k G-FIX G-VAR MIPS-PT G-POT (Pearson et al. ) (G-FIX with dynamic truncation) (Souvenir et al. ) (Potential- function greedy) #Primers CPU sec 8 7 0. 04 7 0. 08 8 10 6 0. 10 10 9 0. 03 10 0. 08 13 15 9 0. 08 12 14 0. 04 13 0. 08 18 26 13 0. 11 8 13 0. 13 15 0. 30 21 48 10 0. 32 10 23 0. 22 24 0. 36 30 150 18 0. 33 12 31 0. 14 32 0. 30 41 246 29 0. 28 8 17 0. 49 20 0. 89 32 226 14 0. 58 10 37 0. 37 37 0. 72 50 844 31 0. 75 12 53 0. 59 48 0. 84 75 2601 42 0. 61 APBC 2005 20

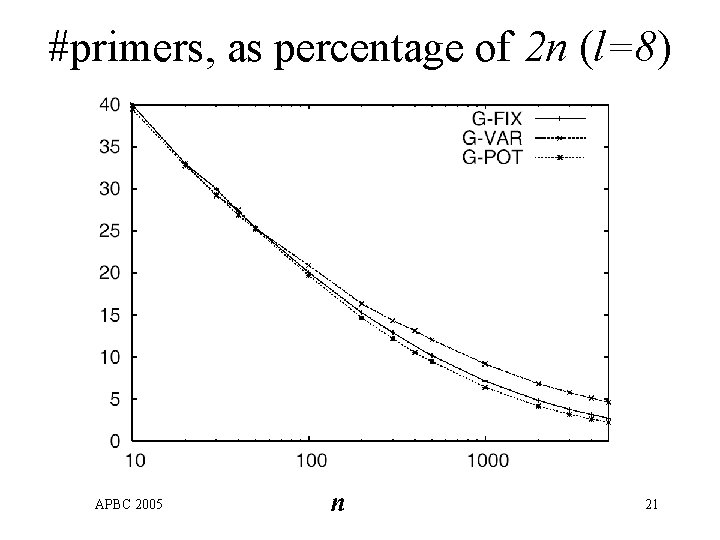
#primers, as percentage of 2 n (l=8) APBC 2005 n 21

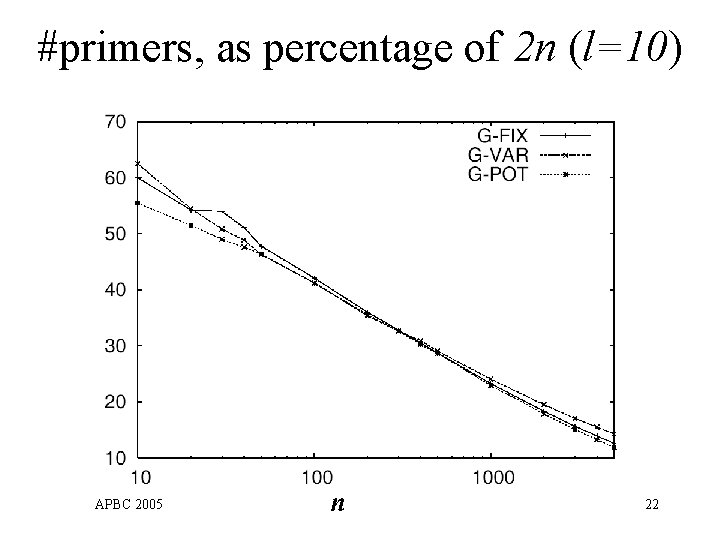
#primers, as percentage of 2 n (l=10) APBC 2005 n 22

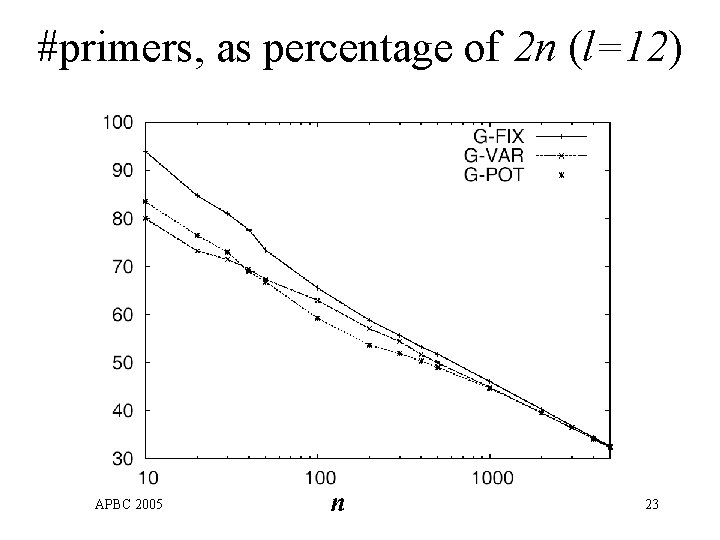
#primers, as percentage of 2 n (l=12) APBC 2005 n 23

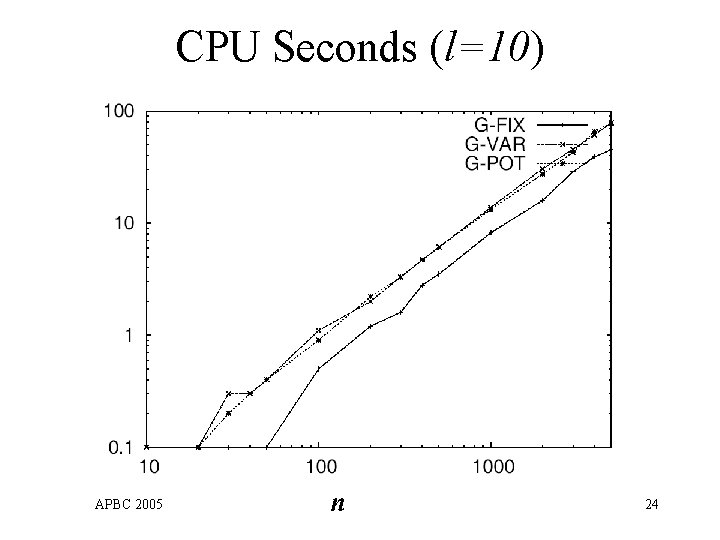
CPU Seconds (l=10) APBC 2005 n 24

Conclusions • Numerous combinatorial optimization problems arising in the area of high-throughput assay design • Theoretical insights such as approximation results can lead to significant practical improvements • Choosing the proper problem model is critical to solution efficiency APBC 2005 25

Ongoing Work & Open Problems • Degenerate primers • Accurate hybridization model (melting temperature, secondary structure, cross hybridization, …) – In-silico MP-PCR simulator • Partition into multiplexed PCR reactions (Aumann et al. Wabi’ 03) APBC 2005 26

Acknowledgments • Financial support from UCONN’s Research Foundation APBC 2005 27