Impossibility of Consensus in Asynchronous Systems FLP Ali

Impossibility of Consensus in Asynchronous Systems (FLP) Ali Ghodsi – UC Berkeley / KTH alig(at)cs. berkeley. edu

Modified Model n A correct node can always make a “dummy” transition q q n For state s of a node, there exists a transition s s There exists always an applicable event on every process There are no inbufs/outbufs, q q q There is one set of messages M, i. e. “network cloud” Message consists of <sender, payload, destination> Messages are unique Ali Ghodsi, alig(at)cs. berkeley. edu 2

Configurations n Each configuration contains the state of each node, and q n The set of messages in the network, M Initial config is a config where M is empty and all nodes are in initial state Configuration < ate, Ali Ghodsi, alig(at)cs. berkeley. edu ate, p 1_st p 2_st p 3_st 3

Events, Applicable, Executions… n An event <p, m> is the receipt of message m q n <p, m> applicable in config C iff q n After the receipt of m, node p deterministically updates its state (transition function) and puts sent messages in M m is in C. M Execution is a sequence of configurations q An applicable event is applied between configs Ali Ghodsi, alig(at)cs. berkeley. edu 4

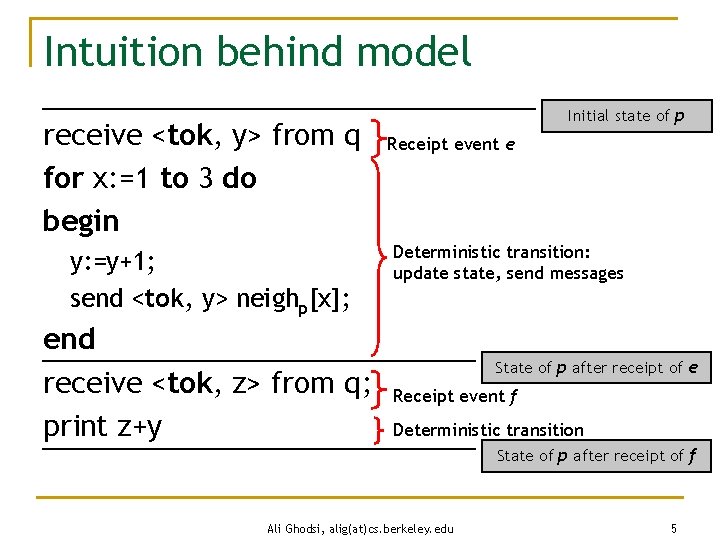
Intuition behind model receive <tok, y> from q for x: =1 to 3 do begin y: =y+1; send <tok, y> neighp[x]; end receive <tok, z> from q; print z+y Initial state of p Receipt event e Deterministic transition: update state, send messages State of p after receipt of e Receipt event f Deterministic transition State of p after receipt of f Ali Ghodsi, alig(at)cs. berkeley. edu 5

Consensus Correctness (weak) n A 1 -crash-robust consensus satisfies: q Termination n q Agreement n q All correct nodes eventually decide In every config, decided nodes have decided same value (0 or 1) Non-triviality (weak validity) n n There exists one possible input config with outcome decision 0, and There exists one possible input config with outcome decision 1 q q Example, maybe input “ 0, 0, 1”->0 while “ 0, 1, 1”->1 Validity implies non-triviality (” 0, 0, 0” must be 0 and ” 1, 1, 1” must be 1) Ali Ghodsi, alig(at)cs. berkeley. edu 6

Definitions n 0 -decided configuration q n 1 -decided configuration q n A config in which every reachable decided configuration is a 0 -decide 1 -valent configuration q n A configuration with decide ” 1” on some process 0 -valent configuration q n A configuration with decide ” 0” on some process A config in which every reachable decided configuration is a 1 -decide Bivalent configuration q A configuration which can reach a 0 -decided and 1 -decided configuration Ali Ghodsi, alig(at)cs. berkeley. edu 7

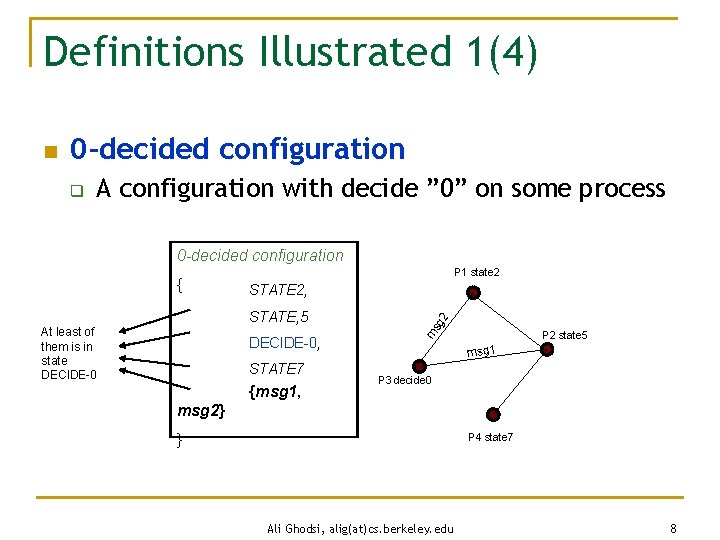
Definitions Illustrated 1(4) n 0 -decided configuration q A configuration with decide ” 0” on some process 0 -decided configuration P 1 state 2 STATE, 5 At least of them is in state DECIDE-0, STATE 7 {msg 1, g 2 STATE 2, ms { P 2 state 5 msg 1 P 3 decide 0 msg 2} } P 4 state 7 Ali Ghodsi, alig(at)cs. berkeley. edu 8

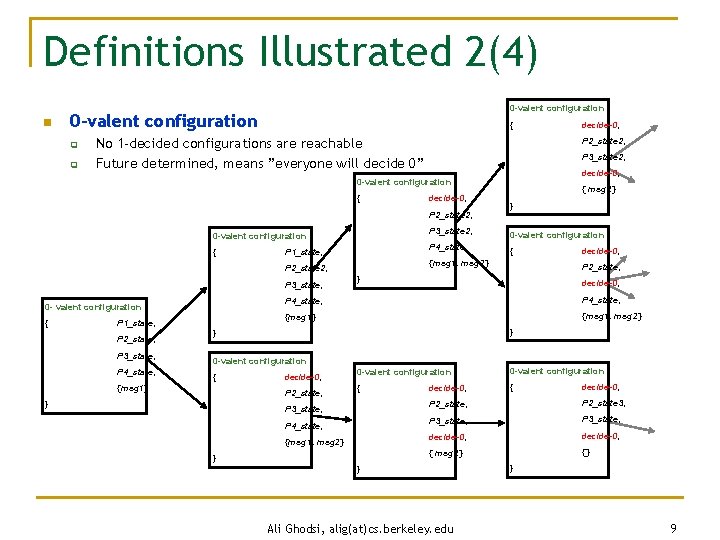
Definitions Illustrated 2(4) n 0 -valent configuration q q { No 1 -decided configurations are reachable Future determined, means ”everyone will decide 0” P 2_state 2, P 3_state 2, decide-0, 0 -valent configuration { decide-0, P 2_state 2, 0 -valent configuration { P 1_state, P 3_state, 0 - valent configuration { P 1_state, P 2_state, P 3_state, P 4_state, 0 -valent configuration P 4_state, { decide-0, P 4_state, {msg 1} {msg 1, msg 2} } decide-0, P 2_state, } 0 -valent configuration {msg 1} } P 3_state 2, } { { msg 2} {msg 1, msg 2} P 2_state 2, decide-0, 0 -valent configuration { { P 3_state, P 4_state, {msg 1, msg 2} } decide-0, P 2_state, P 2_state 3, P 3_state, decide-0, { msg 2} {} } Ali Ghodsi, alig(at)cs. berkeley. edu } 9

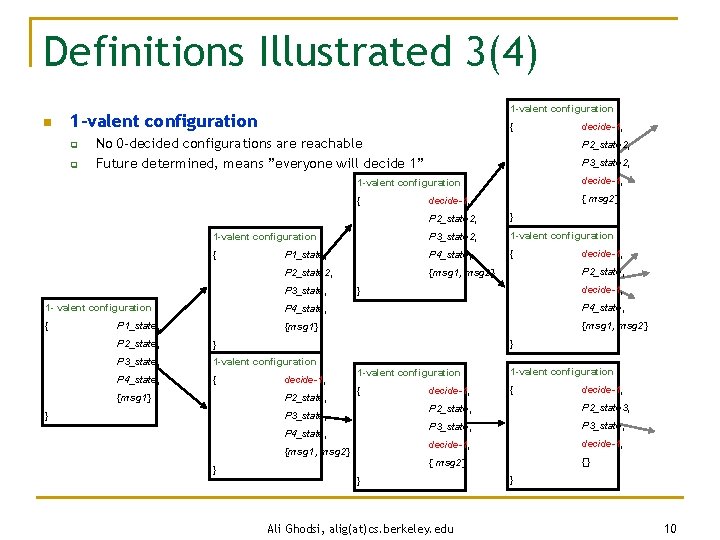
Definitions Illustrated 3(4) n 1 -valent configuration q q { No 0 -decided configurations are reachable Future determined, means ”everyone will decide 1” decide-1, P 2_state 2, P 3_state 2, 1 -valent configuration decide-1, { { msg 2} decide-1, P 2_state 2, } 1 -valent configuration P 3_state 2, 1 -valent configuration { P 1_state, P 4_state, { P 2_state 2, {msg 1, msg 2} P 3_state, decide-1, P 2_state, decide-1, } 1 - valent configuration P 4_state, { {msg 1} {msg 1, msg 2} P 1_state, } P 2_state, } P 3_state, 1 -valent configuration P 4_state, { decide-1, P 2_state, {msg 1} 1 -valent configuration { { P 3_state, } P 4_state, {msg 1, msg 2} } decide-1, P 2_state, P 2_state 3, P 3_state, decide-1, { msg 2} {} } Ali Ghodsi, alig(at)cs. berkeley. edu } 10

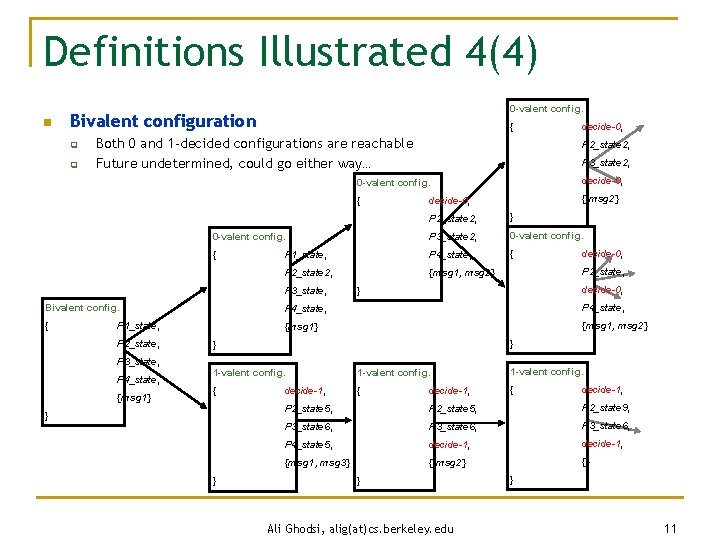
Definitions Illustrated 4(4) n 0 -valent config. Bivalent configuration q q { Both 0 and 1 -decided configurations are reachable Future undetermined, could go either way… decide-0, P 2_state 2, P 3_state 2, 0 -valent config. decide-0, { { msg 2} decide-0, P 2_state 2, } 0 -valent config. P 3_state 2, 0 -valent config. { P 1_state, P 4_state, { P 2_state 2, {msg 1, msg 2} P 3_state, decide-0, P 2_state, decide-0, } Bivalent config. P 4_state, { {msg 1} {msg 1, msg 2} P 1_state, P 2_state, } } P 3_state, P 4_state, {msg 1} 1 -valent config. { { { } } decide-1, P 2_state 5, P 2_state 9, P 3_state 6, P 4_state 5, decide-1, {msg 1, msg 3} { msg 2} {} } Ali Ghodsi, alig(at)cs. berkeley. edu } 11

FLP Impossibility Without Proofs

Bivalent Initial Configuration n Initial Bivalency Lemma (Lemma 1) q Any algorithm that solves the 1 -crash consensus has an initial bivalent configuration Ali Ghodsi, alig(at)cs. berkeley. edu 13

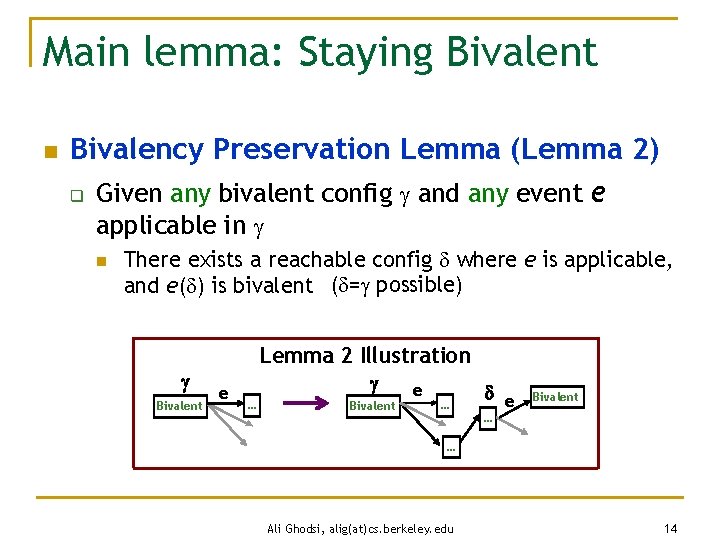
Main lemma: Staying Bivalent n Bivalency Preservation Lemma (Lemma 2) q Given any bivalent config and any event e applicable in n There exists a reachable config where e is applicable, and e( ) is bivalent ( = possible) Lemma 2 Illustration Bivalent e … Bivalent e … e Bivalent … … Ali Ghodsi, alig(at)cs. berkeley. edu 14

FLP Impossibility Theorem n n No deterministic 1 -crash-robust consensus algorithm exists for the asynchronous model Proof 1. Start in a initial bivalent config (Lemma 1) 2. Given the bivalent config, pick the event e that has been applicable longest n n Pick the path taking us to another config where e is applicable (might be empty) Apply e, and get a bivalent config (Lemma 2) 3. Repeat 2. Termination violated Ali Ghodsi, alig(at)cs. berkeley. edu 15

FLP Impossibility Proofs

Bivalent Initial Configuration n Initial Bivalency Lemma (Lemma 1) q Any algorithm that solves the 1 -crash consensus has an initial bivalent configuration Ali Ghodsi, alig(at)cs. berkeley. edu 17

Proof 1/(10) n We know that the algorithm must be nontrivial q q n There should be some initial configuration that will lead to a 0 -decide There should be some initial configuration that will lead to a 1 -decide Take two such configuration i 1 and i 2 q E. g. 4 processes n n initial values (0, 1, 1) lead to 1 Initial values (0, 0, 1, 0, 0) lead to 0 Ali Ghodsi, alig(at)cs. berkeley. edu 18

Proof 2/(10) n We know there exists inputs p 1 , p 2 , p 3 , p 4 , p 5 q (0, 1, 1) leading to 1 q (0, 0, 1, 0, 0) leading to 0 Lets look at other initial configurations by flipping the inputs transforming the upper input to the lower input Ali Ghodsi, alig(at)cs. berkeley. edu 19

Proof 3/(10) n We know there exists inputs p 1 , p 2 , p 3 , p 4 , p 5 q (0, 1, 1) leading to 1 (0, 0, 0, 1, 1) leading to ? q (0, 0, 1, 0, 0) leading to 0 q Lets look at other initial configurations by flipping the inputs transforming the upper input to the lower input Ali Ghodsi, alig(at)cs. berkeley. edu 20

Proof 4/(10) n We know there exists inputs p 1 , p 2 , p 3 , p 4 , p 5 q (0, 1, 1) leading to 1 (0, 0, 0, 1, 1) leading to ? (0, 0, 1, 1, 1) leading to ? q (0, 0, 1, 0, 0) leading to 0 q q Lets look at other initial configurations by flipping the inputs transforming the upper input to the lower input Ali Ghodsi, alig(at)cs. berkeley. edu 21

Proof 5/(10) n We know there exists inputs p 1 , p 2 , p 3 , p 4 , p 5 q q q (0, 1, 1) leading to 1 (0, 0, 0, 1, 1) leading to ? (0, 0, 1, 0, 0) leading to 0 Lets look at other initial configurations by flipping the inputs transforming the upper input to the lower input Ali Ghodsi, alig(at)cs. berkeley. edu 22

Proof 6/(10) n We know there exists inputs p 1 , p 2 , p 3 , p 4 , p 5 q q q (0, 1, 1) (0, 0, 1, 0, 1) (0, 0, 1, 0, 0) leading leading to to to 1 ? ? ? 0 Lets look at other initial configurations by flipping the inputs transforming the upper input to the lower input There must exist two neighboring configurations here, with two different outcomes Ali Ghodsi, alig(at)cs. berkeley. edu 23

Proof 7/(10) n We know there exists inputs p 1 , p 2 , p 3 , p 4 , p 5 q q q (0, 1, 1) (0, 0, 1, 0, 1) (0, 0, 1, 0, 0) leading leading to to to 1 1 1 0 0 Lets look at other initial configurations by flipping the inputs Assume the following two Ali Ghodsi, alig(at)cs. berkeley. edu 24

Proof 8/(10) n We know there exists inputs p 1 , p 2 , p 3 , p 4 , p 5 q q q (0, 1, 1) (0, 0, 1, 0, 1) (0, 0, 1, 0, 0) leading leading to to to 1 1 1 0 0 Assume the following two Identical configurations except for process p 4 Ali Ghodsi, alig(at)cs. berkeley. edu 25

Proof 9/(10) n We know there exists inputs p 1 , p 2 , p 3 , p 4 , p 5 q q n (0, 0, 1, 1, 1) leading to 1 (0, 0, 1) leading to 0 Assume the following two The consensus algorithm should tolerate if p 4 crashes! q (0, 0, 1, X, 1), leads to ? (either 0 or 1) Ali Ghodsi, alig(at)cs. berkeley. edu 26

Proof 10/(10) n We know there exists inputs p 1, p 2, p 3, p 4, p 5 q q n (0, 0, 1, 1, 1) leading to 1 (0, 0, 1) leading to 0 Assume the following two The consensus algorithm should tolerate if p 4 crashes! q q q (0, 0, 1, X, 1), leads to ? (either 0 or 1) If it leads to 1, then depending on whether (0, 0, 1) either leads to 0 or 1 (bivalent) p 4 crashes or not If it leads to 0, then depending on whether (0, 0, 1, 1, 1) either leads to 0 or 1 (bivalent) p 4 crashes or not Ali Ghodsi, alig(at)cs. berkeley. edu 27

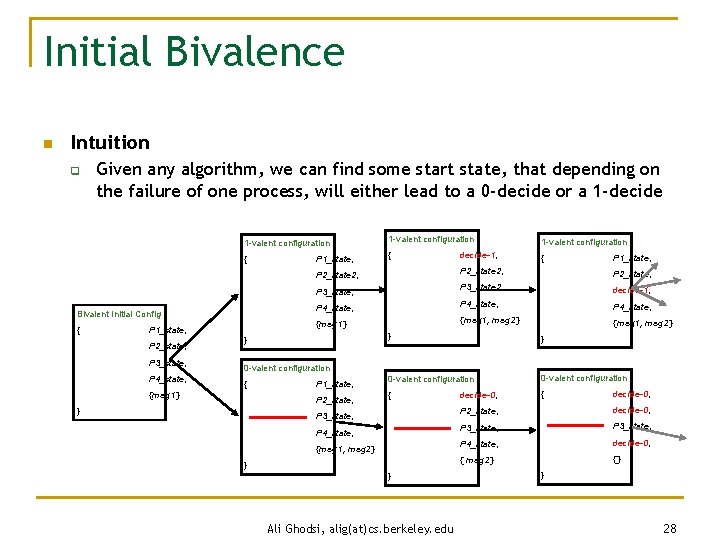
Initial Bivalence n Intuition q Given any algorithm, we can find some start state, that depending on the failure of one process, will either lead to a 0 -decide or a 1 -decide 1 -valent configuration { { { Bivalent Initial Config { P 1_state, P 2_state, P 3_state, P 4_state, P 1_state, decide-1, P 2_state 2, P 2_state, P 3_state 2, decide-1, P 4_state, {msg 1} {msg 1, msg 2} } 0 -valent configuration { {msg 1} P 1_state, P 2_state, } P 1_state, P 2_state 2, P 3_state, P 4_state, {msg 1, msg 2} } } Ali Ghodsi, alig(at)cs. berkeley. edu decide-0, P 2_state, decide-0, P 3_state, P 4_state, decide-0, { msg 2} {} } 28

Order of events n Intuition q n The order in which two applicable events are executed is not important! Order Theorem q Let ep and eq be two events on two different nodes p and q which are both applicable in config C, then n ep can be applied to eq(C), eq can be applied to ep(C), and ep(eq(C)) = eq(ep(C) ). Ali Ghodsi, alig(at)cs. berkeley. edu 29

Definitions n A schedule is a sequence of events <e 1, e 2, …, ek> n A schedule =<e 1, e 2, …, ek> is applicable in config C iff n q e 1 is applicable in C, q e 2 is applicable in e 1(C) q e 3 is applicable in e 2(e 1(C)) q . . . If the resulting config is D we write (C)=D Ali Ghodsi, alig(at)cs. berkeley. edu 30

Order of sequences n Diamond Theorem q Let sequences 1 and 2 be applicable in configuration C, and let no node participate in both 1 and 2, then: n n 2 is applicable in 1(C) 1 is applicable in 2(C), and 1( 2(C))= 2( 1(C)) Proof q By induction using the order theorem Ali Ghodsi, alig(at)cs. berkeley. edu 31

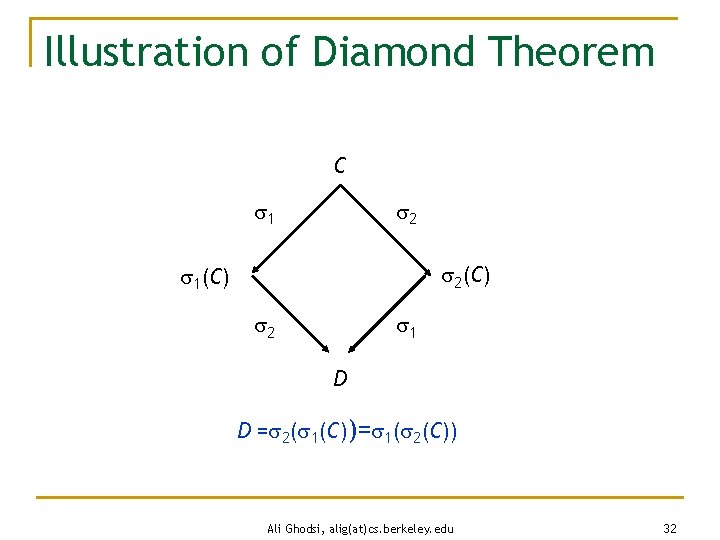
Illustration of Diamond Theorem C 1 2 2(C) 1(C) 2 1 D D = 2( 1(C))= 1( 2(C)) Ali Ghodsi, alig(at)cs. berkeley. edu 32

Bivalent Configuration n Any configuration of the 1 -robust consensus algorithm is exactly one of these three q q q n Bivalent 0 -valent 1 -valent Why? q q q Any configuration leads to a decide (termination) We know bivalent configurations exist If it is not bivalent, it must lead to either 0 -decide or 1 decide, so it is either 0 -valent or 1 -valent Ali Ghodsi, alig(at)cs. berkeley. edu 33

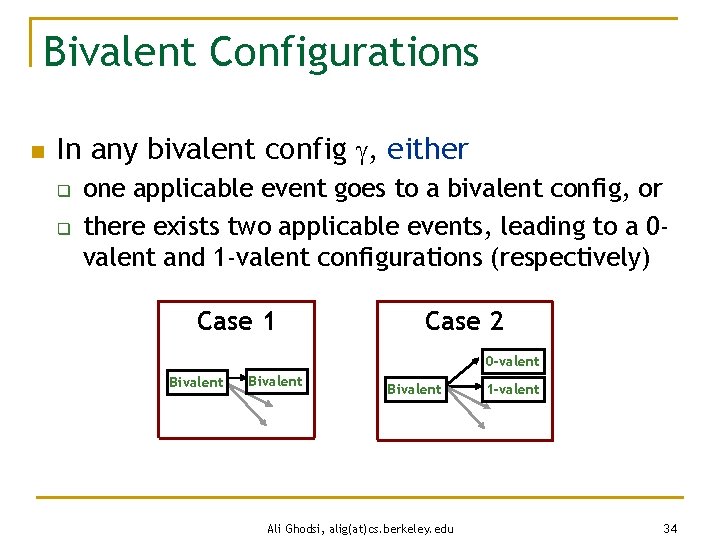
Bivalent Configurations n In any bivalent config , either q q one applicable event goes to a bivalent config, or there exists two applicable events, leading to a 0 valent and 1 -valent configurations (respectively) Case 1 Case 2 0 -valent Bivalent Ali Ghodsi, alig(at)cs. berkeley. edu 1 -valent 34

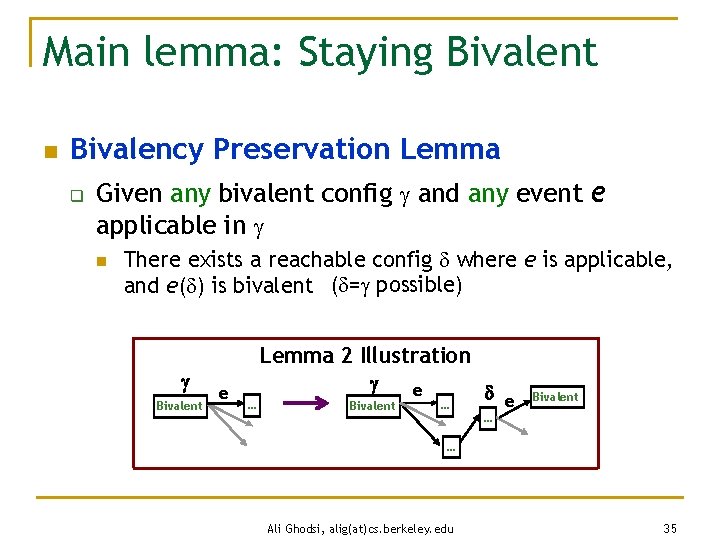
Main lemma: Staying Bivalent n Bivalency Preservation Lemma q Given any bivalent config and any event e applicable in n There exists a reachable config where e is applicable, and e( ) is bivalent ( = possible) Lemma 2 Illustration Bivalent e … Bivalent e … e Bivalent … … Ali Ghodsi, alig(at)cs. berkeley. edu 35

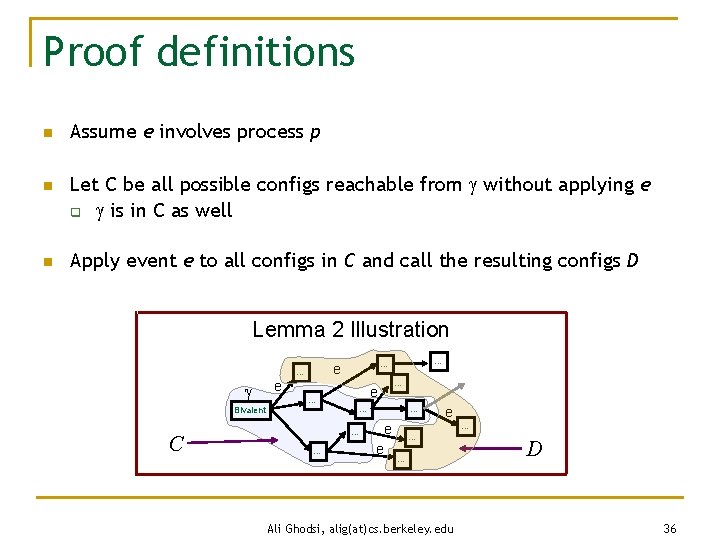
Proof definitions n n n Assume e involves process p Let C be all possible configs reachable from without applying e q is in C as well Apply event e to all configs in C and call the resulting configs D Lemma 2 Illustration Bivalent C e … … e e … … … … e … … … Ali Ghodsi, alig(at)cs. berkeley. edu D 36

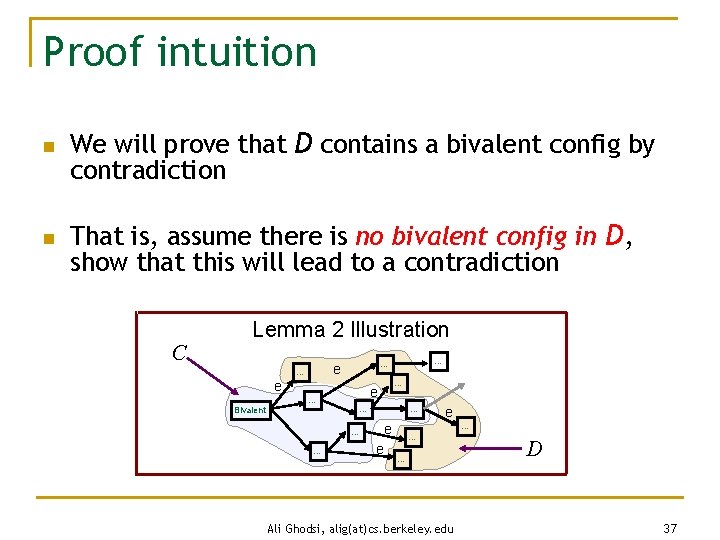
Proof intuition n We will prove that D contains a bivalent config by contradiction n That is, assume there is no bivalent config in D, show that this will lead to a contradiction C Lemma 2 Illustration e Bivalent … … e e … … … … e … … … Ali Ghodsi, alig(at)cs. berkeley. edu D 37

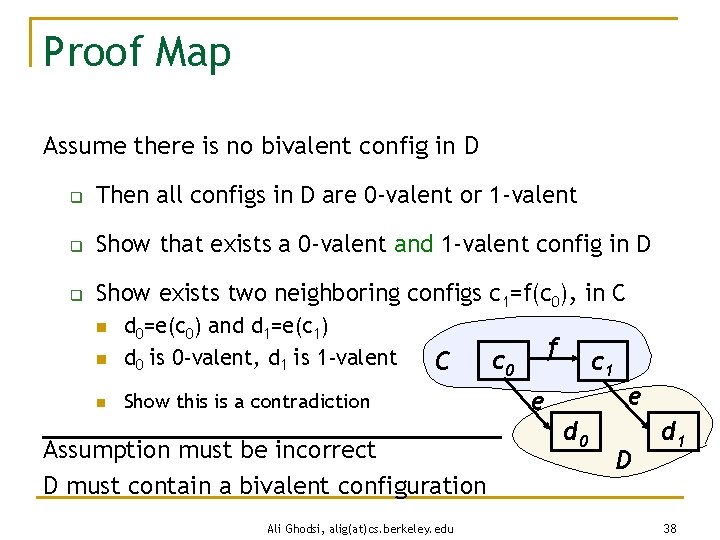
Proof Map Assume there is no bivalent config in D q Then all configs in D are 0 -valent or 1 -valent q Show that exists a 0 -valent and 1 -valent config in D q Show exists two neighboring configs c 1=f(c 0), in C n d 0=e(c 0) and d 1=e(c 1) d 0 is 0 -valent, d 1 is 1 -valent n Show this is a contradiction n C Assumption must be incorrect D must contain a bivalent configuration Ali Ghodsi, alig(at)cs. berkeley. edu f c 0 c 1 e e d 0 D d 1 38

Proof n n Assume D contains no bivalent configs q i. e. all configs in D are either 0 -valent or 1 -valent We next show that there q exists a 0 -valent config in D, and there exists a 1 -valent config in D Ali Ghodsi, alig(at)cs. berkeley. edu 39

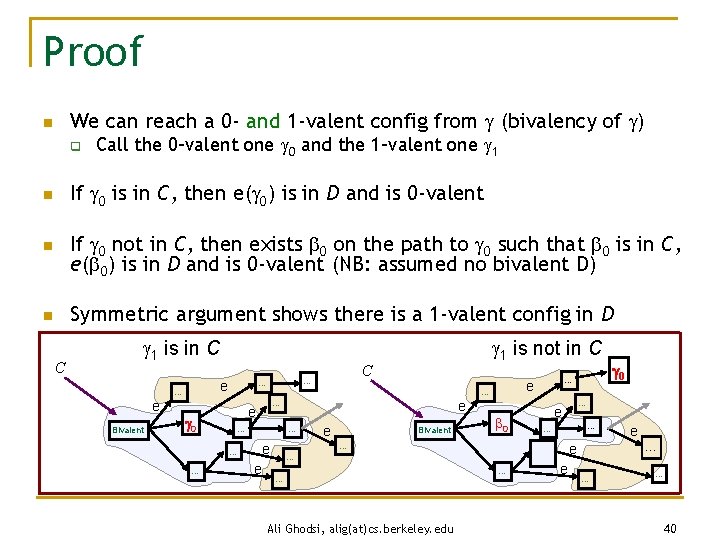
Proof We can reach a 0 - and 1 -valent config from (bivalency of ) n q Call the 0 -valent one 0 and the 1 -valent one 1 If 0 is in C, then e( 0) is in D and is 0 -valent n If 0 not in C, then exists 0 on the path to 0 such that 0 is in C, e( 0) is in D and is 0 -valent (NB: assumed no bivalent D) n Symmetric argument shows there is a 1 -valent config in D n C 1 is in C … e Bivalent 0 … … e … Bivalent 0 … … … Ali Ghodsi, alig(at)cs. berkeley. edu … e e … 0 … e e e … … e … C … … e 1 is not in C … … 40

Reflection n Now we know D must contain q n a 0 -valent and a 1 -valent config Call the 0/1 -valent configs in D: d 0 and d 1 Ali Ghodsi, alig(at)cs. berkeley. edu 41

Deriving the contradiction n There must exist two configs c 0 and c 1 in C such that c 1=f(c 0), and d 0=e(c 0) and d 1 = e( c 1 ) C f c 0 c 1 e e d 0 n Let’s see why! D d 1 Ali Ghodsi, alig(at)cs. berkeley. edu 42

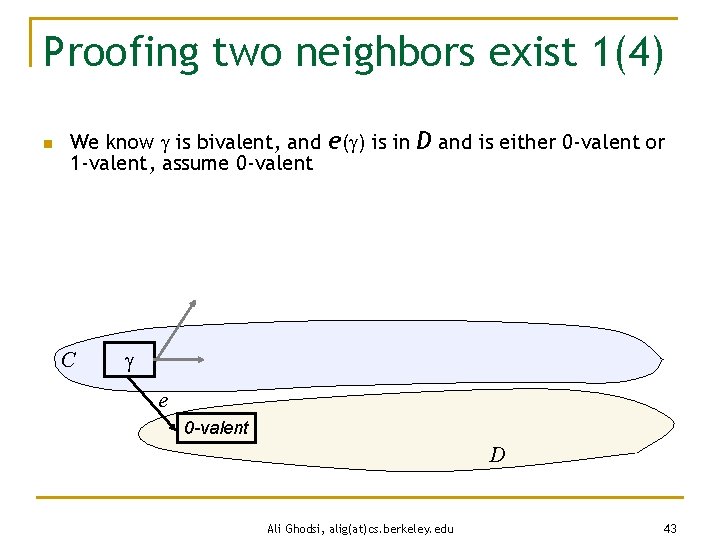
Proofing two neighbors exist 1(4) n We know is bivalent, and e( ) is in D and is either 0 -valent or 1 -valent, assume 0 -valent C e 0 -valent D Ali Ghodsi, alig(at)cs. berkeley. edu 43

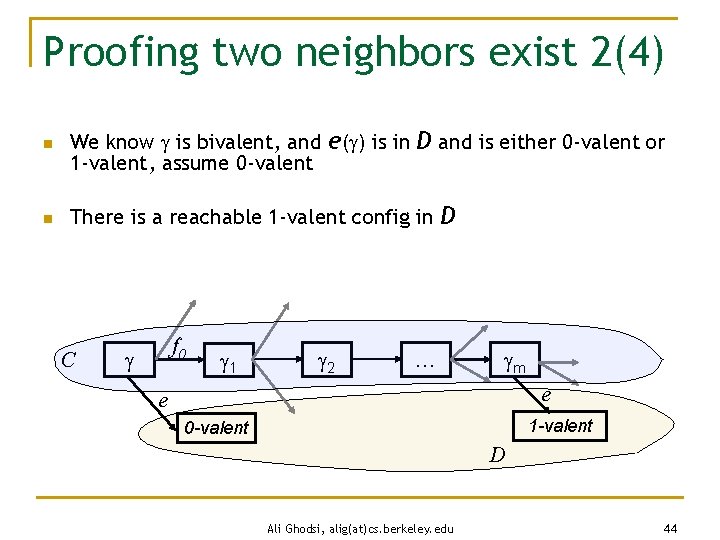
Proofing two neighbors exist 2(4) n We know is bivalent, and e( ) is in D and is either 0 -valent or 1 -valent, assume 0 -valent n There is a reachable 1 -valent config in D C f 0 1 2 … m e e 1 -valent 0 -valent D Ali Ghodsi, alig(at)cs. berkeley. edu 44

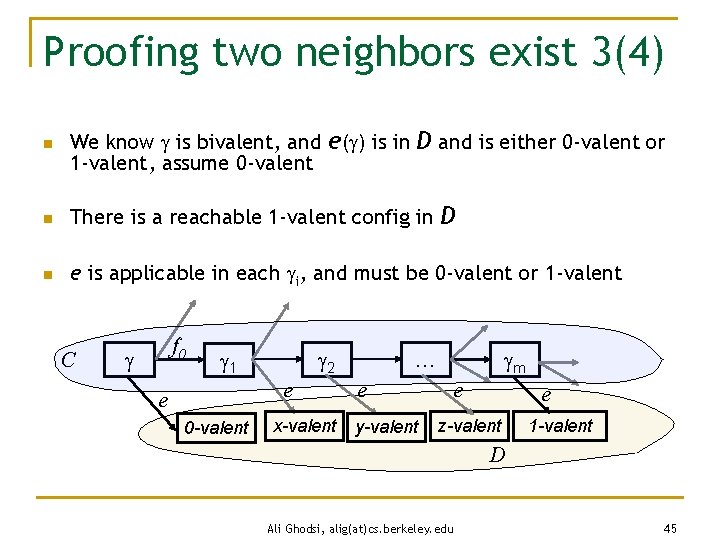
Proofing two neighbors exist 3(4) n We know is bivalent, and e( ) is in D and is either 0 -valent or 1 -valent, assume 0 -valent n There is a reachable 1 -valent config in D n e is applicable in each i, and must be 0 -valent or 1 -valent C f 0 2 1 e e 0 -valent x-valent m … e y-valent e e z-valent 1 -valent D Ali Ghodsi, alig(at)cs. berkeley. edu 45

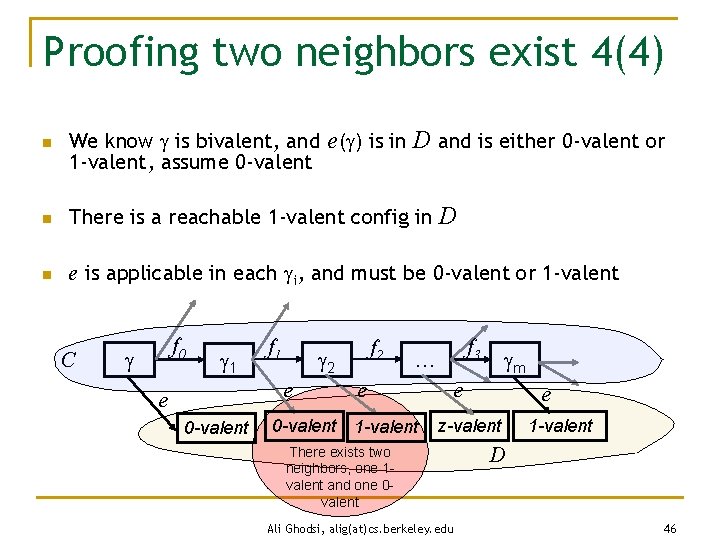
Proofing two neighbors exist 4(4) n We know is bivalent, and e( ) is in D and is either 0 -valent or 1 -valent, assume 0 -valent n There is a reachable 1 -valent config in D n e is applicable in each i, and must be 0 -valent or 1 -valent C f 0 1 f 1 e e 0 -valent f 2 2 0 -valent f 3 … e 1 -valent m e e z-valent There exists two neighbors, one 1 valent and one 0 valent Ali Ghodsi, alig(at)cs. berkeley. edu 1 -valent D 46

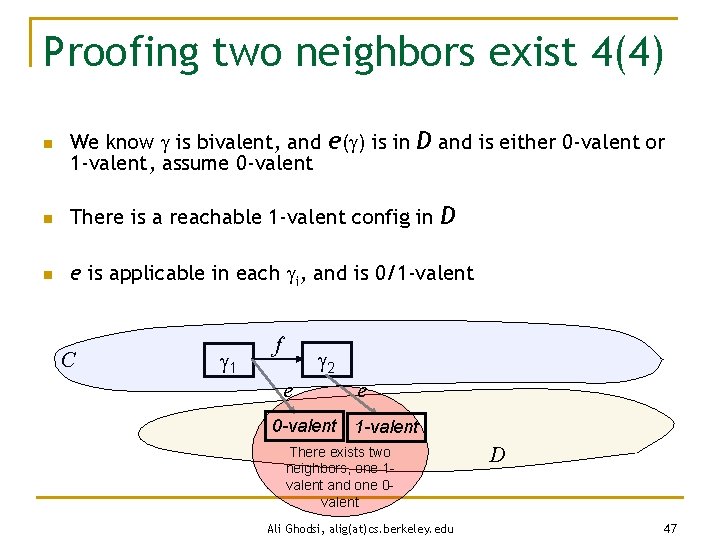
Proofing two neighbors exist 4(4) n We know is bivalent, and e( ) is in D and is either 0 -valent or 1 -valent, assume 0 -valent n There is a reachable 1 -valent config in D n e is applicable in each i, and is 0/1 -valent C 1 f 2 e 0 -valent e 1 -valent There exists two neighbors, one 1 valent and one 0 valent Ali Ghodsi, alig(at)cs. berkeley. edu D 47

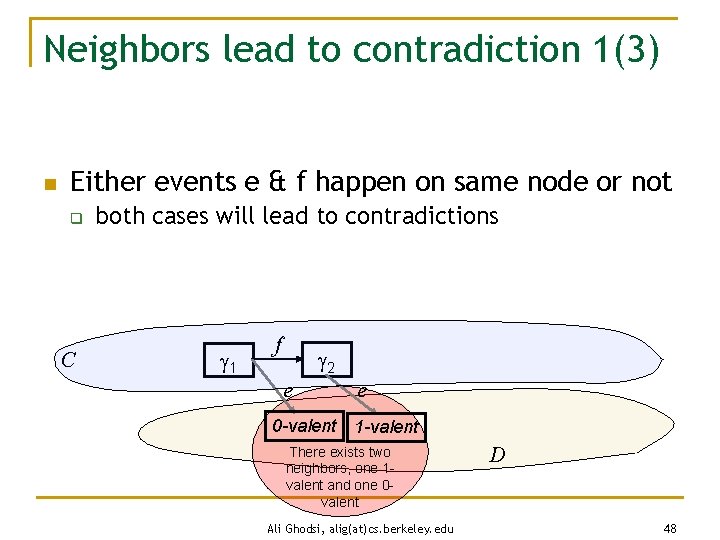
Neighbors lead to contradiction 1(3) n Either events e & f happen on same node or not q C both cases will lead to contradictions 1 f 2 e 0 -valent e 1 -valent There exists two neighbors, one 1 valent and one 0 valent Ali Ghodsi, alig(at)cs. berkeley. edu D 48

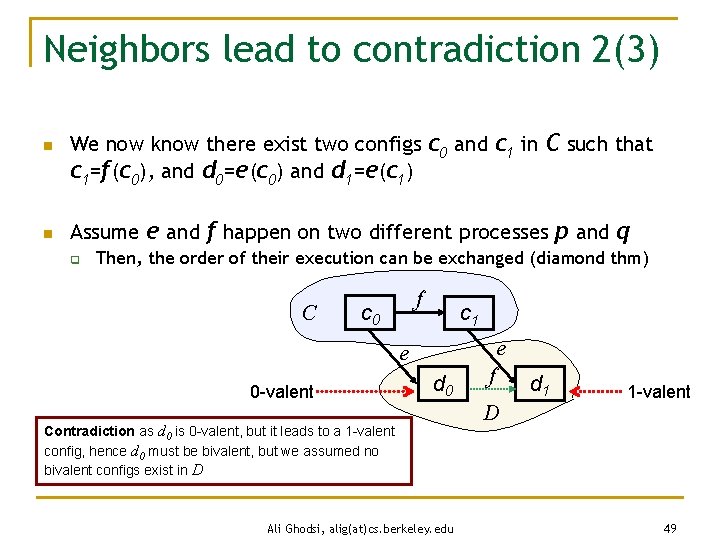
Neighbors lead to contradiction 2(3) n n We now know there exist two configs c 0 and c 1 in C such that c 1=f(c 0), and d 0=e(c 0) and d 1=e(c 1) Assume e and f happen on two different processes p and q q Then, the order of their execution can be exchanged (diamond thm) C f c 0 c 1 e e 0 -valent d 0 Contradiction as d 0 is 0 -valent, but it leads to a 1 -valent config, hence d 0 must be bivalent, but we assumed no bivalent configs exist in D Ali Ghodsi, alig(at)cs. berkeley. edu f D d 1 1 -valent 49

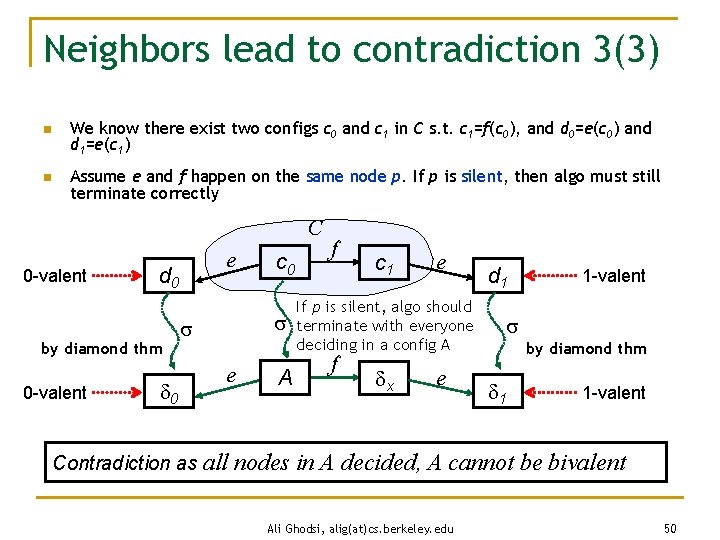
Neighbors lead to contradiction 3(3) n We know there exist two configs c 0 and c 1 in C s. t. c 1=f(c 0), and d 0=e(c 0) and d 1=e(c 1) n Assume e and f happen on the same node p. If p is silent, then algo must still terminate correctly C 0 -valent d 0 by diamond thm 0 -valent e 0 c 0 e Contradiction as all A f c 1 e If p is silent, algo should terminate with everyone deciding in a config A f x e d 1 1 -valent by diamond thm 1 1 -valent nodes in A decided, A cannot be bivalent Ali Ghodsi, alig(at)cs. berkeley. edu 50

FLP Impossibility Theorem n n No deterministic 1 -crash-robust consensus algorithm exists for the asynchronous model Proof 1. Start in a initial bivalent config (Lemma 1) 2. Given the bivalent config, pick the event e that has been applicable longest n Pick the execution taking us to another config where e is applicable Apply e, and get a bivalent config (Lemma 2) 3. Repeat 2. n Ali Ghodsi, alig(at)cs. berkeley. edu 51

Summary n We have proved that a 1 -crash resilient deterministic consensus algorithm does not exist q q n Hence, there exists always an execution which stays in bivalent configs and still keeps applying all applicable events in a fair order! All correct nodes execute infinite number of events, messages delivered, and still leads to no decision! Circumventing FLP impossibility q q q Probabilistically Randomization Partial Synchrony (e. g. failure detectors) Ali Ghodsi, alig(at)cs. berkeley. edu 52