Important ProcessesModels Purely Random Process and Random Walk


- Slides: 7

Important Processes/Models, (Purely Random Process and Random Walk Model) Sadia Qamar

Filters/Operators Important Stochastic Processes Ø A purely Random Process Ø Random Walk Ø Moving Average Process Ø Autoregressive Process Ø A mixed autoregressive-moving average Process

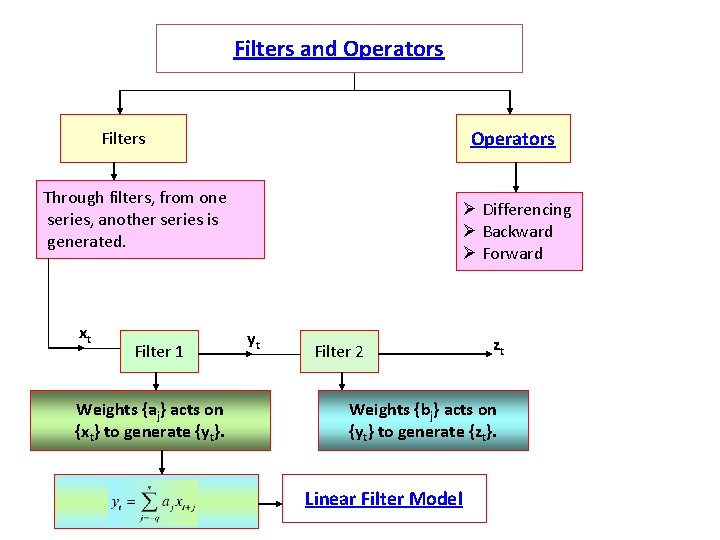
Filters and Operators Filters Through filters, from one series, another series is generated. xt Filter 1 Weights {aj} acts on {xt} to generate {yt}. Ø Differencing Ø Backward Ø Forward yt Filter 2 zt Weights {bj} acts on {yt} to generate {zt}. Linear Filter Model

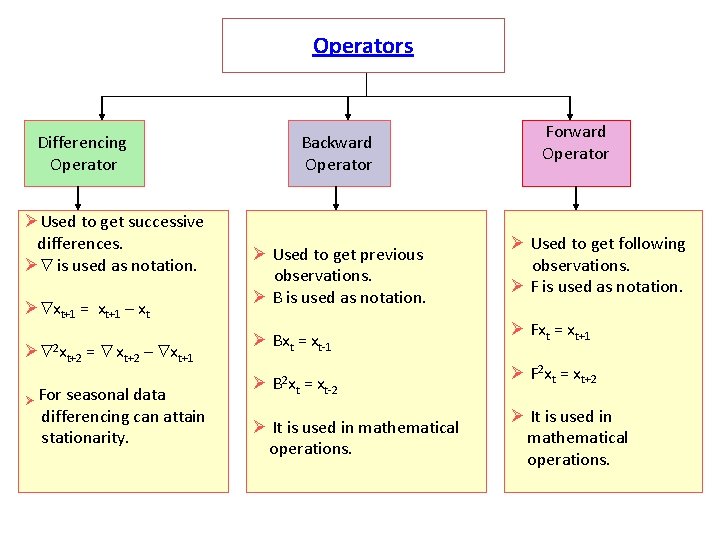
Operators Differencing Operator ØUsed to get successive differences. Ø is used as notation. Ø xt+1 = xt+1 – xt Ø 2 xt+2 = xt+2 – xt+1 Ø For seasonal data differencing can attain stationarity. Backward Operator Ø Used to get previous observations. Ø B is used as notation. Ø Bxt = xt-1 Ø B 2 x t = xt-2 Ø It is used in mathematical operations. Forward Operator Ø Used to get following observations. Ø F is used as notation. Ø Fxt = xt+1 Ø F 2 xt = xt+2 Ø It is used in mathematical operations.

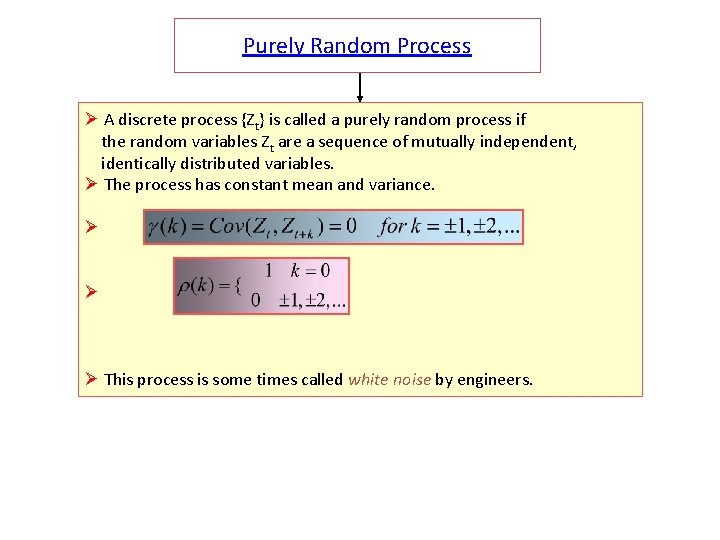
Purely Random Process Ø A discrete process {Zt} is called a purely random process if the random variables Zt are a sequence of mutually independent, identically distributed variables. Ø The process has constant mean and variance. Ø Ø Ø This process is some times called white noise by engineers.

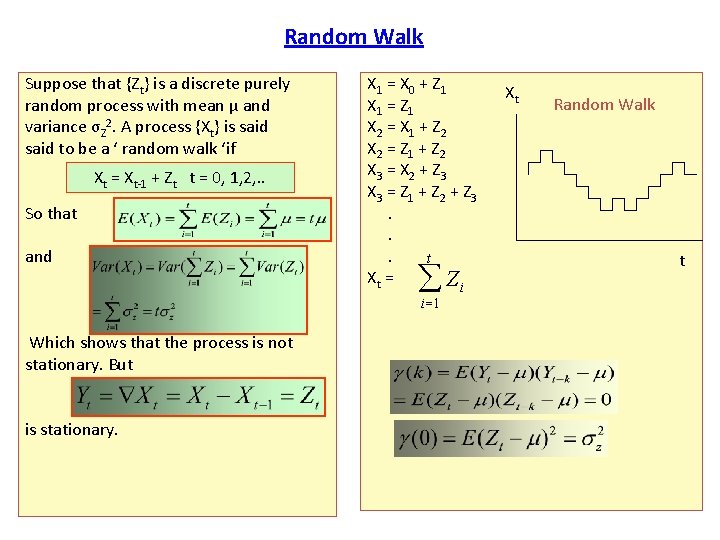
Random Walk Suppose that {Zt} is a discrete purely random process with mean µ and variance σZ 2. A process {Xt} is said to be a ‘ random walk ‘if Xt = Xt-1 + Zt t = 0, 1, 2, . . So that and X 1 = X 0 + Z 1 X 1 = Z 1 X 2 = X 1 + Z 2 X 2 = Z 1 + Z 2 X 3 = X 2 + Z 3 X 3 = Z 1 + Z 2 + Z 3. . . t Xt = Zi Xt Random Walk t å i =1 Which shows that the process is not stationary. But is stationary. 1

Random Walk Continued Random Walk with drift. Ø A simple extension of the random walk process. Ø This process accounts for a trend. Ø The process {Xt} is a random walk with drift if Ø The process on average will tend to move upward for d > 0. Figure Xt Random walk with drift t