Important Notations 04 December 2020 Introduction 1 Notations

Important Notations 04 December 2020 Introduction 1

Notations 04 December 2020 Introduction 2

Complex Numbers • We will extensively use complex numbers throughout this course. • Their use is NOT mandatory. • But the use gives tremendouse convenience in classical wave physics. 04 December 2020 Introduction 3

Complex Numbers Definition : And also satisfied by -i

Complex Numbers Representation & Notation : x & y : real numbers i : unit imaginary number iy : pure imaginary number Now Every algebraic equation can be solved!!
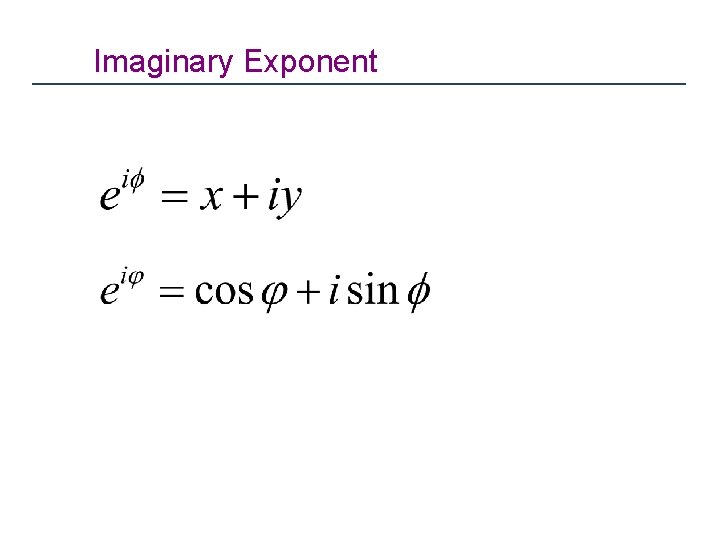
Imaginary Exponent

Formulation Suppose Therefore

Complex Conjugate In general The conjugate

Phasor = Rotating Arrow + Associated Phase Angle
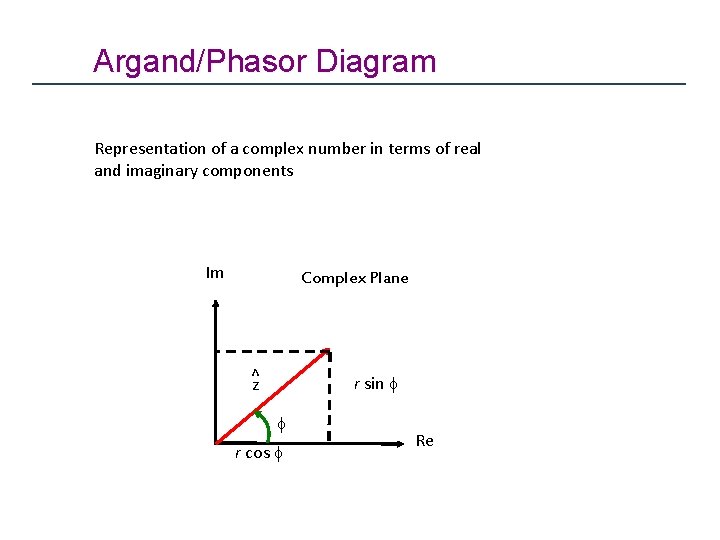
Argand/Phasor Diagram Representation of a complex number in terms of real and imaginary components Im Complex Plane ^ z r sin f f r cos f Re
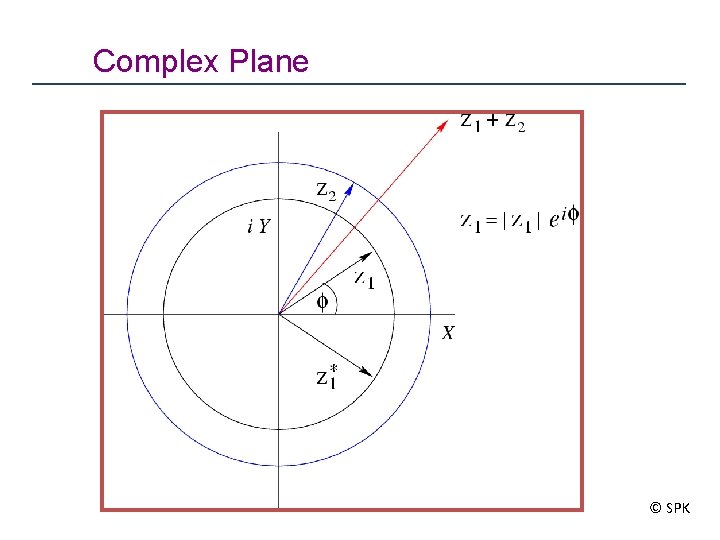
Complex Plane © SPK

Taylor series is a series expansion of a function about a point 1 -d Taylor series expansion of a real function about a point is Maclaurin series is a Taylor series expansion of a function about 0 i. e. , if a = 0, the expansion is known Maclaurin series

Consider the following Maclaurin series expansions Expansions are valid for complex arguments x too Function :
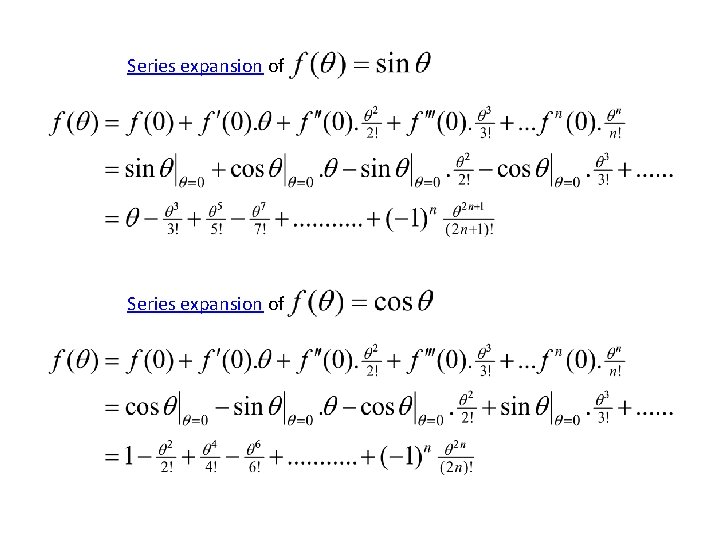
Series expansion of

Series expansion of

Complex Numbers & Simple Harmonic Oscillations

Why Exponential Form? o Both sine & cosine are available in one form, take real or imaginary part o Periodic nature of displacement is reproducible o Leaves the form under differentiation and integration o Algebraic manipulations are quite easy 04 December 2020 Introduction 17

Exponential solution: A=Complex amplitude Real and imaginary parts of z(t) satisfy simple harmonic equation of motion x(t)=Re z(t) 04 December 2020 Introduction 18
![Additions of two SHMs become convenient For, [ 04 December 2020 + Introduction ] Additions of two SHMs become convenient For, [ 04 December 2020 + Introduction ]](http://slidetodoc.com/presentation_image_h/df913674bd44d8a80af34d6599582359/image-19.jpg)
Additions of two SHMs become convenient For, [ 04 December 2020 + Introduction ] 19
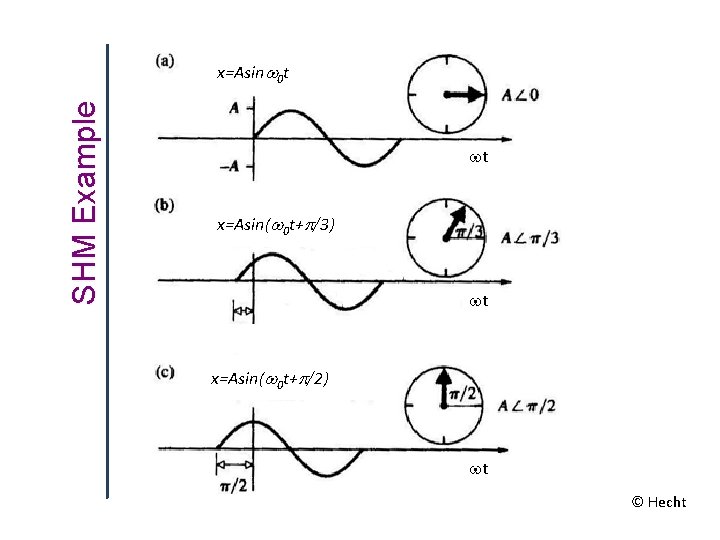
SHM Example x=Asinw 0 t wt x=Asin(w 0 t+p/3) wt x=Asin(w 0 t+p/2) wt © Hecht

Complex Representation © SB

Meaning/Significance The real part of the complex number. Represents the oscillating quantity © SB
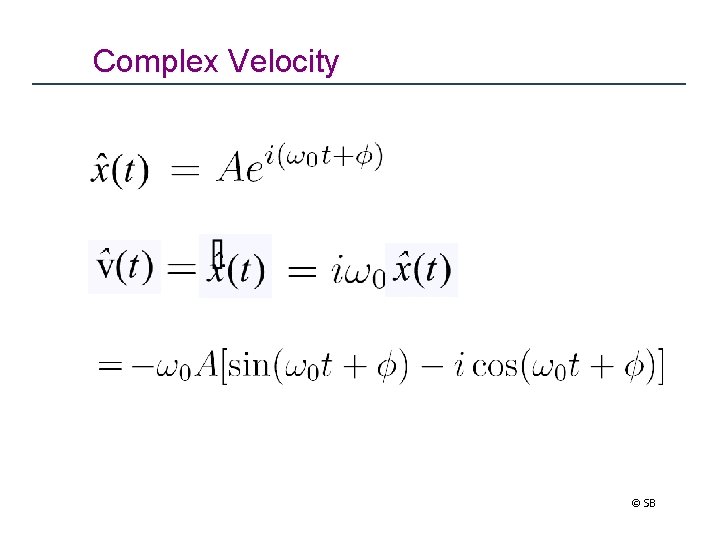
Complex Velocity © SB

Velocity © SB
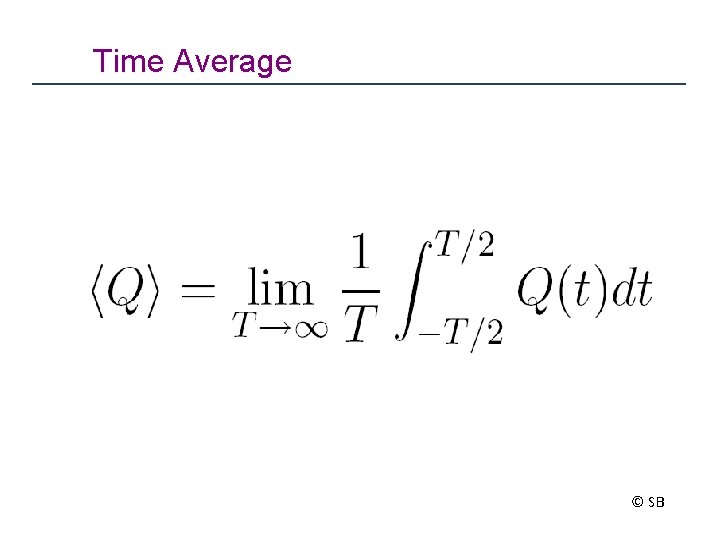
Time Average © SB
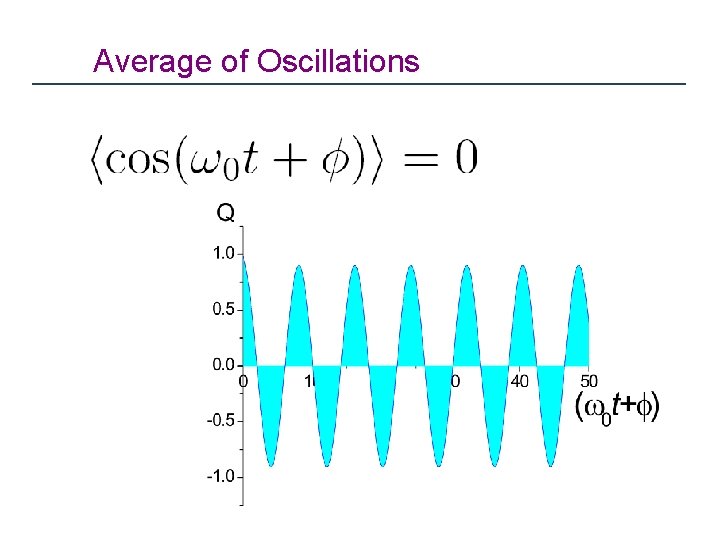
Average of Oscillations
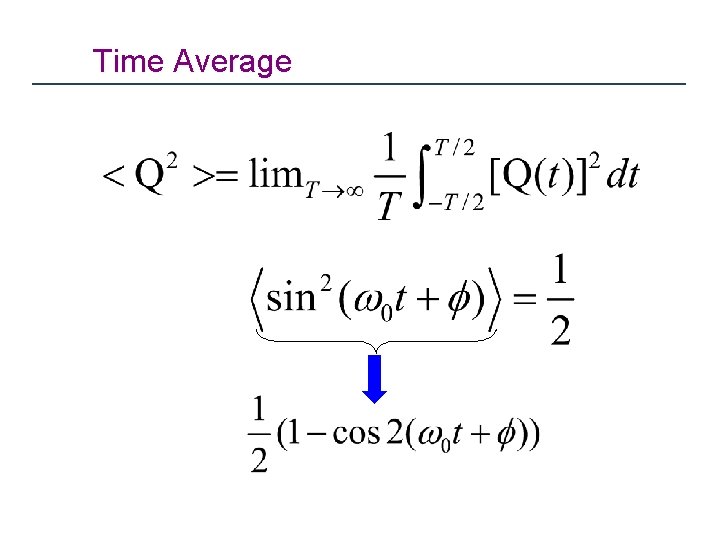
Time Average

Time Average of KE & PE in SHM
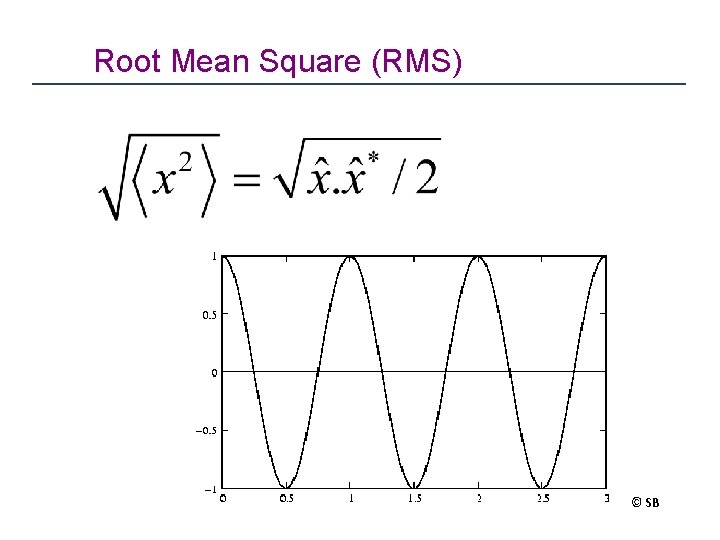
Root Mean Square (RMS) © SB

An Example The natural frequency of a simple harmonic oscillator is 1/p sec-1. Initially (at t=0), the displacement of the oscillator from its equilibrium position is 0. 3 m and velocity 0. 7 m. sec-1. Use complex notation to determine the amplitude and phase of the motion:

Solution

Solution

1. FEYNMAN LECTURES ON PHYSICS VOL I Author : RICHARD P FEYNMAN IIT KGP Central Library : Class no. 530. 4
- Slides: 33