Important concepts in IR spectroscopy Vibrations that result

Important concepts in IR spectroscopy Vibrations that result in change of dipole moment give rise to IR absorptions. The oscillating electric field of the radiation couples with the molecular vibration to cause an alternating electric field produced by the changing dipole. Absorption bands in vibration spectra appear as broad bands (not a single energy) if the rotational states of the molecules are not resolved as it is usually the case in liquid or solid phases. IR absorptions are characteristic of an entire molecule and are as unique as a fingerprint (molecular fingerprint). Many “localized vibrations” help to identify functional groups. Band intensities are expressed as either transmission (T) or absorption (A) A = log 10(1/T) In addition to fundamental transitions, IR spectra can contain overtone bands, due to excitation into higher vibrational states, and combination bands, due to coupling of two or several “group” vibrations. Group vibrations can couple if their frequencies are similar and they share a common atom. A special case of coupling occurs when a fundamental vibration couples with an overtone or combination vibration. This phenomenon is known as Fermi resonance.

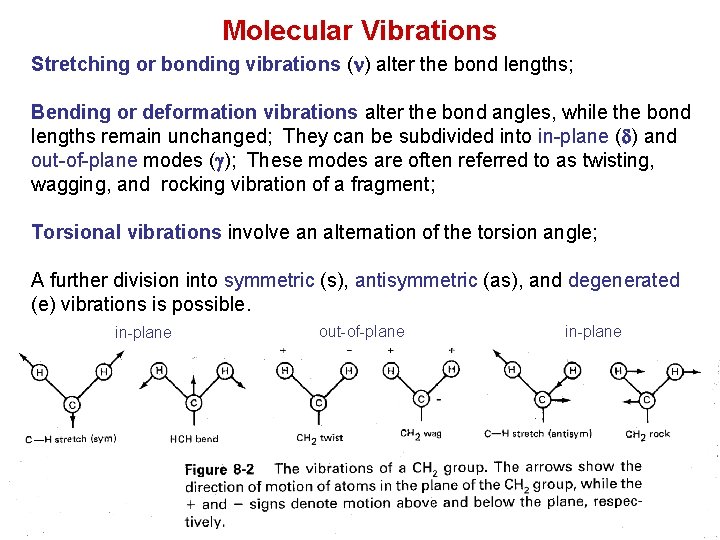
Molecular Vibrations Stretching or bonding vibrations (n) alter the bond lengths; Bending or deformation vibrations alter the bond angles, while the bond lengths remain unchanged; They can be subdivided into in-plane (d) and out-of-plane modes (g); These modes are often referred to as twisting, wagging, and rocking vibration of a fragment; Torsional vibrations involve an alternation of the torsion angle; A further division into symmetric (s), antisymmetric (as), and degenerated (e) vibrations is possible. in-plane out-of-plane in-plane

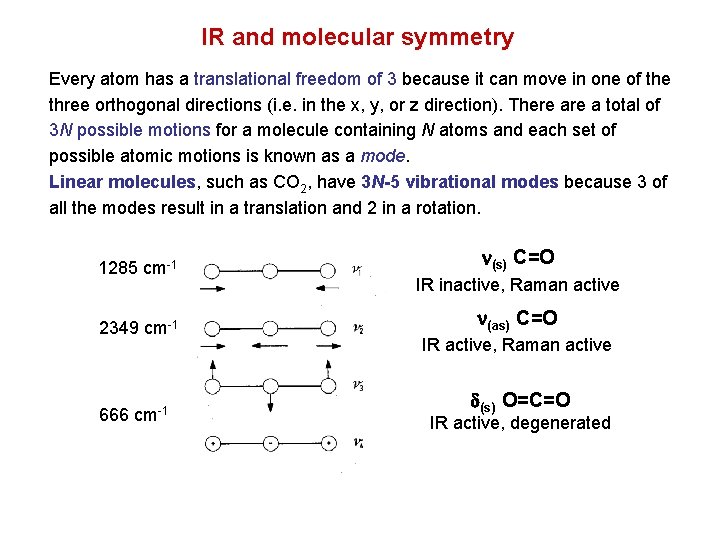
IR and molecular symmetry Every atom has a translational freedom of 3 because it can move in one of the three orthogonal directions (i. e. in the x, y, or z direction). There a total of 3 N possible motions for a molecule containing N atoms and each set of possible atomic motions is known as a mode. Linear molecules, such as CO 2, have 3 N-5 vibrational modes because 3 of all the modes result in a translation and 2 in a rotation. 1285 cm-1 2349 cm-1 666 cm-1 n(s) C=O IR inactive, Raman active n(as) C=O IR active, Raman active d(s) O=C=O IR active, degenerated

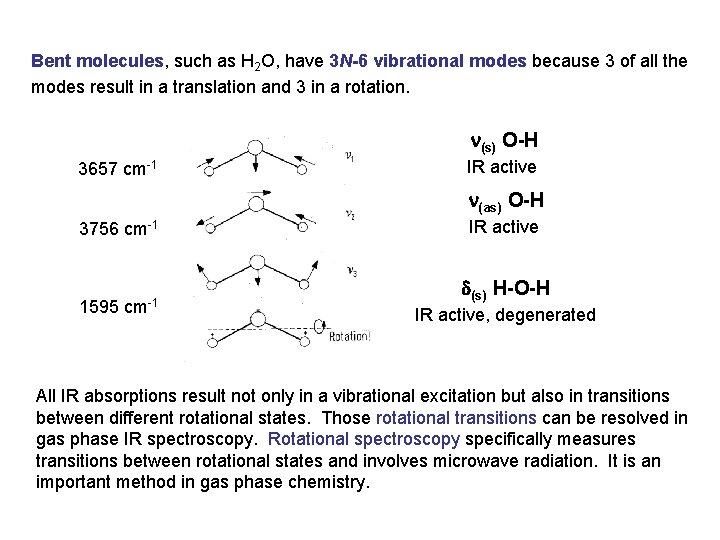
Bent molecules, such as H 2 O, have 3 N-6 vibrational modes because 3 of all the modes result in a translation and 3 in a rotation. n(s) O-H 3657 cm-1 IR active n(as) O-H 3756 cm-1 1595 cm-1 IR active d(s) H-O-H IR active, degenerated All IR absorptions result not only in a vibrational excitation but also in transitions between different rotational states. Those rotational transitions can be resolved in gas phase IR spectroscopy. Rotational spectroscopy specifically measures transitions between rotational states and involves microwave radiation. It is an important method in gas phase chemistry.

59 -250, notes 6, Macdonald Vibrational Spectroscopy and Symmetry Example, the vibrational modes in water. The E operation leaves everything where it is so all nine vectors stay in the same place and the character is 9. z y x The C 2 operation moves both H atoms so we can ignore the vectors on those atoms, but we have to look at the vectors on the oxygen atom, because it is still in the same place. The vector in the z direction does not change (+1) but the vectors in the x, and y directions are reversed (-1 and -1) so the character for C 2 is -1. The v (xz) operation leaves each atom where it was so we have to look at the vectors on each atom. The vectors in the z and x directions do not move (+3 and +3) but the vectors in the y direction are reversed (-3) so the character is 3. The ’v (yz) operation moves both H atoms so we can ignore the vectors on those atoms, but we have to look at the vectors on the oxygen atom, because it is still in the same place. The vectors in the z and y directions do not move (+1 and +1) but the vectors in the x direction is reversed (-1) so the character is 1. C 2 V E C 2 v (xz) ’v (yz) tot 9 -1 3 1 C 2 v (xz) ’v (yz)

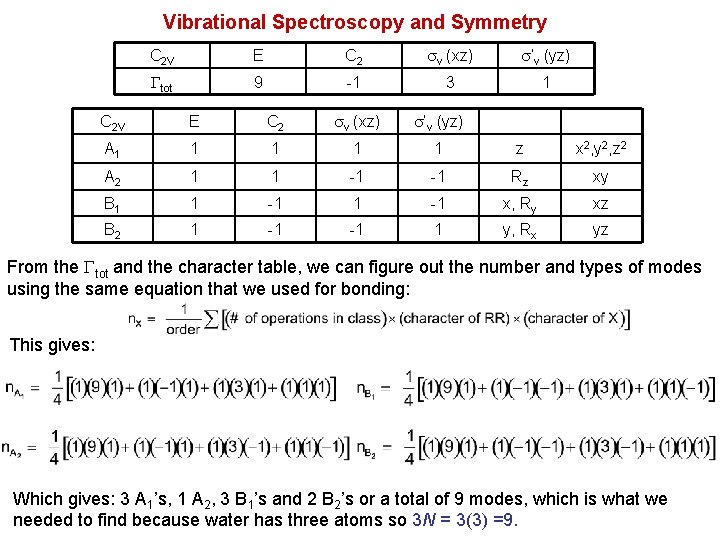
Vibrational Spectroscopy and Symmetry C 2 V E C 2 v (xz) ’v (yz) tot 9 -1 3 1 C 2 V E C 2 v (xz) ’v (yz) A 1 1 1 z x 2, y 2, z 2 A 2 1 1 -1 -1 Rz xy B 1 1 -1 x, Ry xz B 2 1 -1 -1 1 y, Rx yz From the tot and the character table, we can figure out the number and types of modes using the same equation that we used for bonding: This gives: Which gives: 3 A 1’s, 1 A 2, 3 B 1’s and 2 B 2’s or a total of 9 modes, which is what we needed to find because water has three atoms so 3 N = 3(3) =9.

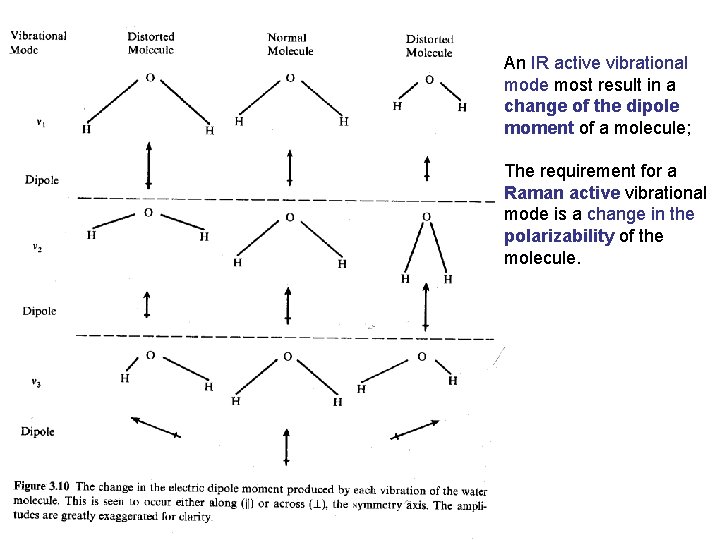
An IR active vibrational mode most result in a change of the dipole moment of a molecule; The requirement for a Raman active vibrational mode is a change in the polarizability of the molecule.

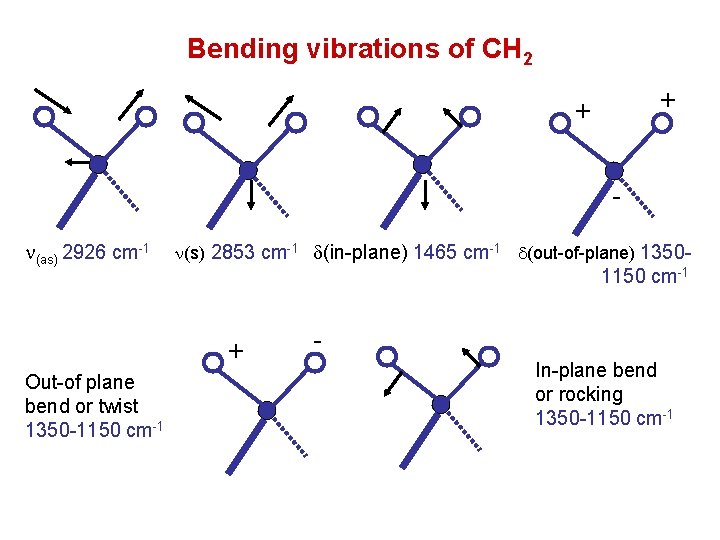
Bending vibrations of CH 2 + + n(as) 2926 cm-1 n(s) 2853 cm-1 d(in-plane) 1465 cm-1 d(out-of-plane) 1350 - 1150 cm-1 + Out-of plane bend or twist 1350 -1150 cm-1 In-plane bend or rocking 1350 -1150 cm-1

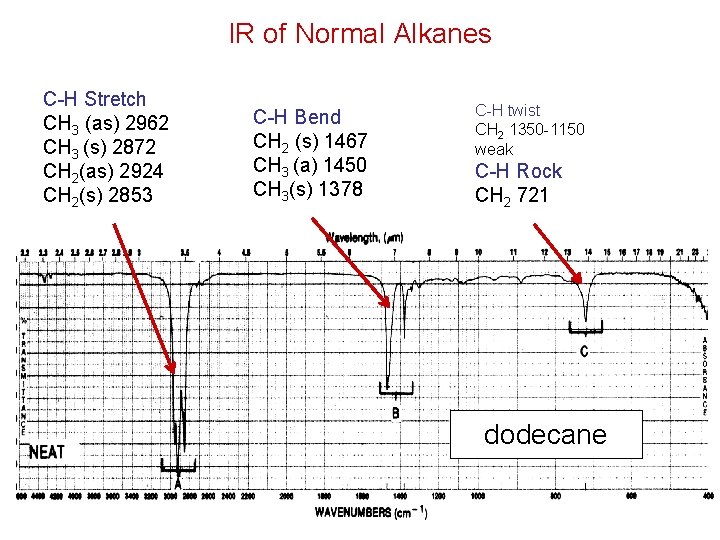
IR of Normal Alkanes C-H Stretch CH 3 (as) 2962 CH 3 (s) 2872 CH 2(as) 2924 CH 2(s) 2853 C-H Bend CH 2 (s) 1467 CH 3 (a) 1450 CH 3(s) 1378 C-H twist CH 2 1350 -1150 weak C-H Rock CH 2 721 dodecane

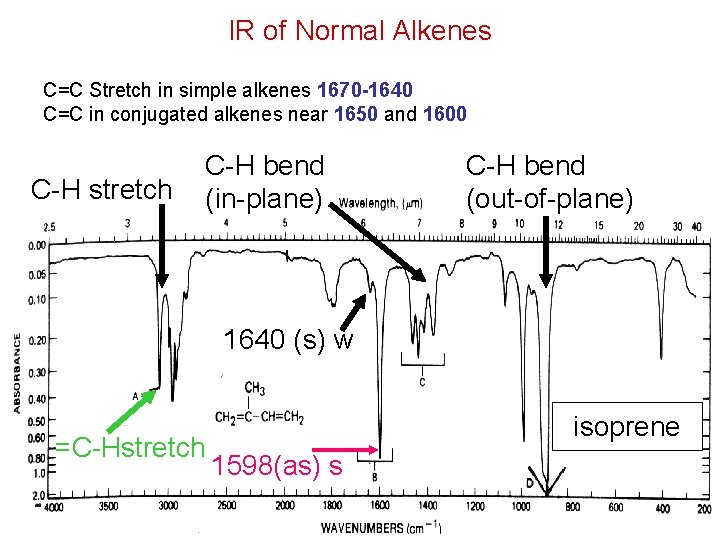
IR of Normal Alkenes C=C Stretch in simple alkenes 1670 -1640 C=C in conjugated alkenes near 1650 and 1600 C-H stretch C-H bend (in-plane) C-H bend (out-of-plane) 1640 (s) w =C-Hstretch isoprene 1598(as) s

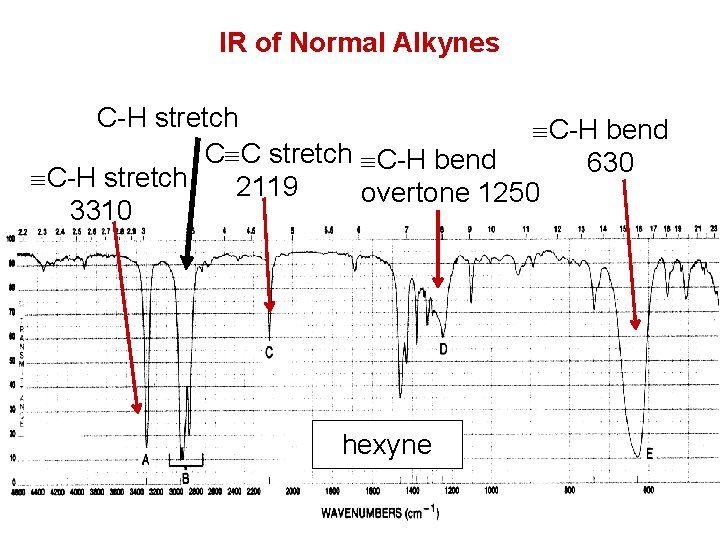
IR of Normal Alkynes C-H stretch ºC-H bend CºC stretch ºC-H bend 630 ºC-H stretch 2119 overtone 1250 3310 hexyne