Implicit Methods Patrick Quirk February 10 2005 Introduction

Implicit Methods Patrick Quirk February 10, 2005

Introduction, Motivation • Explicit methods have a difficult time with some types of ODE’s • They guess where the function is heading • Stiff ODE’s – – – One component big for a short time Does not contribute later Must make time step small for explicit to handle it

Solution – Implicit Methods • Backward Euler Method • Evaluates ƒ at the point we’re aiming at – Less guessing, more accuracy • Consequently, the step size can be larger

Implicit Methods • Last example was simplisitc • Typically cannot directly solve for yn+1 – Unless ƒ is linear • So…approximate ƒ with its Taylor Expansion

Implicit Methods • More equation manipulations are done • Allows us to approximate Δx – Albeit with an inverse of a matrix! • In general this extra computation isn’t bad – Larger time step offsets this

An Aside - Explicit Method • Verlet Algorithm • Does away with the velocity term – Stores only current, previous position – Approximates velocity by xn-xn-1

An Aside - Explicit Method • But it’s explicit! – It’s a second-order method, higher accuracy – Has the computational cost of a first-order – No numerical drift like in some other explicit and implicit methods – Easy to code! – Widely used in games and physics – Often chosen over implicit methods for these reasons

Big Picture - Implicit Methods • • • Explicit Method code is easy Implicit Method code is harder Try to make problem un-stiff if possible – Then use an explicit method and small Δt • Otherwise write an implicit solver – Use the larger time step to your advantage

Second Order ODEs • Dynamics problems are often second order • Need to convert it to a first order problem

Second Order ODEs • Introduce new variables to get first order • But this gives a 2 nx 2 n linear system – Bad news for BEM, has to solve that system – Can we reduce the size?

Second Order ODEs • Can reduce it to nxn – Introduce some more new variables • Taylor Expand ƒ (in two dimensions) – Put that back into the equation

Second Order ODEs • Substitute the first row into the second • Regroup terms and solve for Δv • If there is a variance in time, an extra term:

Sources • SIGGRAPH Course Notes – • Mathworld References – • http: //mathworld. wolfram. com “A Practical Dynamics System”. Kačić-Alesić, Nordenstam, Bullock. Eurographics/SIGGRAPH 2003. – • http: //www. pixar. com/companyinfo/research/pbm 2001/notesd. pdf http: //portal. acm. org/citation. cfm? id=846276. 846278 “Advanced Character Physics”. Thomas Jakobsen. Gamasutra. 2003 – http: //www. gamasutra. com/resource_guide/20030121/jacobson_01. shtml

Interactive Animation of Structured Deformable Objects Mathieu Desbrun, Peter Schröder, Alan Barr Caltech

Introduction, Motivation • Interactive deformation is tough – Simulation methods are too slow – Usually used in VR, user has control • Limited greatly by time step – Too big means instability in simulation – Too small means alteration in reality • Implicit Integration – Offers low computational time – Nearly arbitrary time step

Implicit Integration : 1 D case n+1 • Replace all forces at time t by t+1 • Now positions are not blindly reached, but are logically inferred. In other words: • Explicit steps into the unknown with only initial conditions. • Implicit tries to hit the next position correctly.

Implicit Integration : 1 D case • Must compute Fn+1 at t+dt (spring forces) • Use a first order approximation (since we don’t know what exactly Fn+1(t+dt) is) • Here Δn+1 x is called the backward difference operator:

Implicit Integration : 1 D case • Add artificial viscosity – Increases stability • Force filtering – Uses matrix multiplication (H=d. F/dx) – Global force effects – Smoothes large force differences • Pull it all together…

Implicit Integration : 1 D case • Final Form for 1 D: Damping Force Filter Matrix • Look closely, is it really implicit?

Implicit Integration : 1 D case • Loss in accuracy – Force smoothing – Artificial viscosity • Force filtering matrix changes at each time step (2 D/3 D only) – Forces you to solve a linear system • Gain in speed

Implicit Integration: 1 D case • Some of the “Bads” aren’t all that bad: • Artificial viscosity – It is frequently added to simulations. – If it is already taken care of, so much the better. • Changing filter matrix – Even if this does take time, the computational advantages are already so significant it doesn’t matter too much. – Approximating it makes it a constant • Compute it once, use it forever

Implicit Integration: 2 D/3 D case • Similar to 1 D case, though the smoothing matrix changes with each step. – This paper removes the need to solve a linear system • Splits the force into a linear and non-linear part – Linear is easily solved, non-linear approximated to zero • Magnitude does not change (internal forces), just direction • • Preserve linear/angular momenta Includes inverse dynamics to remove stretching

Implicit Integration : 2 D/3 D case • In 2 D/3 D, implicit integration is done by computing the Hessian matrix H – It depends on position of particle nodes, changing • Equation for one element of H is too long to show here – Each node is a 3 x 3 matrix, total of 3 nx 3 n elements • Too large to solve efficiently – Approximate it

Implicit Integration : 2 D/3 D case • Matrix split into 2 parts – Linear – Non-Linear • Simple, assume its zero • It’s constant in magnitude, but will rotate

Implicit Integration : 2 D/3 D case • Check if linear, angular momenta are conserved – Linear is • Sum of artificial viscosity forces is zero • Force filtering has no effect – Angular is not! • Because of that assumption about the non-linear hessian • Desbrun corrects this with some inverse dynamics
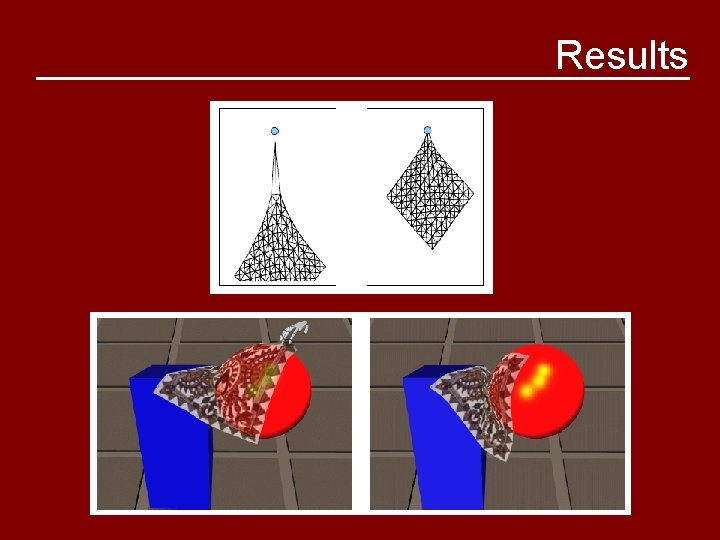
Results
Sources • “Interactive Animation of Structured Deformable Objects”. Desbrun, Schröder, Barr. Graphics Interface. 1999 – http: //www. multires. caltech. edu/pubs/GI 99. pdf
- Slides: 27