IMPLEMENTING SYNCHRONOUS MODELS ON LOOSELY TIME TRIGGERED ARCHITECTURES

IMPLEMENTING SYNCHRONOUS MODELS ON LOOSELY TIME TRIGGERED ARCHITECTURES Discussed by Alberto Puggelli

OUTLINE From synchronous to LTTA Analysis of system throughput

SYNCHRONOUS IS GOOD… Predictability Theoretical backing Easy verification Automated synthesis …. .

… BUT DIFFICULT TO IMPLEMENT! Need for clock synchronization in embedded systems � Long wires � Cheap hardware � Timing constraints

SOLUTION Complete all verification steps in the synchronous domain De-synchronize the system while preserving the semantic Stream Equivalence Preservation

STEPS TO DESYNCHRONIZE Design the system with sync semantic Choose a suitable architecture Platform Based Design: select a set of intermediate layers to map the system description on the architecture while preserving the semantic

ARCHITECTURE: LTTA Loosely Time Triggered Architecture Each node has an independent clock and it can write and read to the medium asynchronously The medium is a shared memory, that is refreshed synchronously to the medium clock Neither blocking read nor blocking write � Each node has to check for the presence of data in the medium (reading) and for the availability of memory (writing)

INTERMEDIATE LAYER: FFP Kahn Process Network with bounded FIFOs (to represent a real system) Marked Directed Graphs (MDG) to allow semantic preservation and to analyze system performance

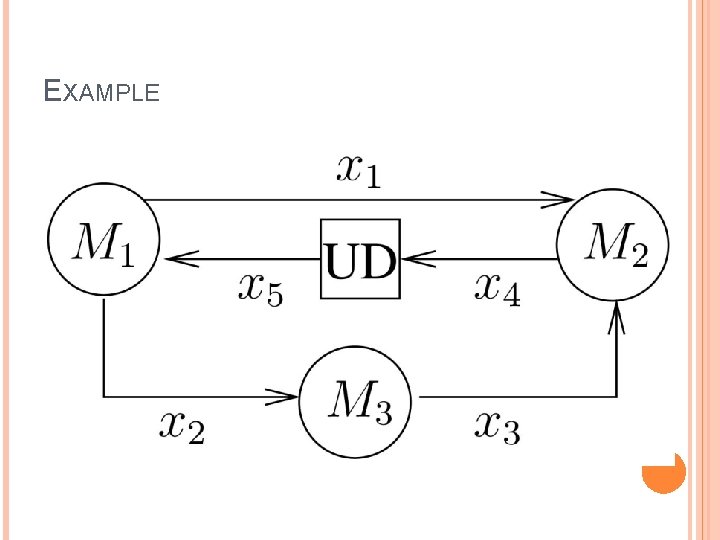
SYNCHRONOUS MODEL Set of Mealy machines and connections among them directed graph (nodes & edges) Every loop is broken by a unit-delay element (UD) Partial order: Mi < Mj if there is a link from Mi to Mj without UD (reflexive and transitive) Minimal element: Mi if there is no Mj s. t. Mj < Mi Each link is an infinite stream of values in V (also UD has output streams) Each machine produce an output and a next state as a function of the inputs and of the current state For UD y(k+1) = x(k) y(0) = i. v. (x input, y output) Firing the machines in any total order that respects the partial order

EXAMPLE

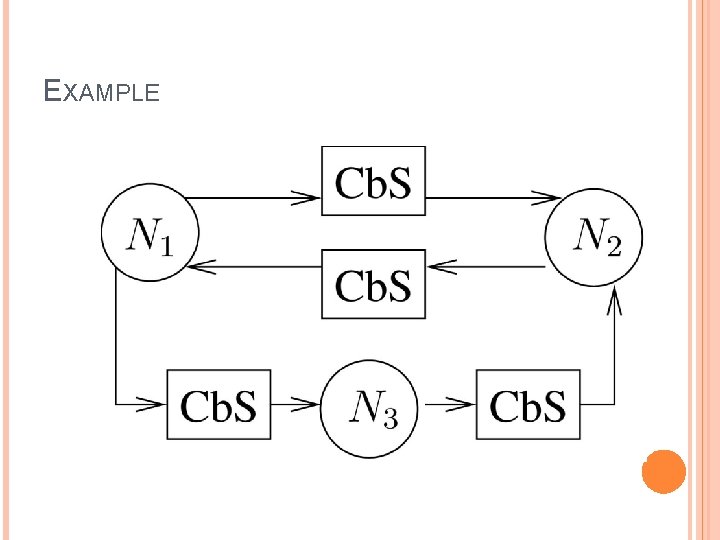
ARCHITECTURE: LTTA Each node runs a single process triggered by a local clock. Communication by Sampling (Cb. S) links among nodes. API: set of functions to call Cb. S. These functions can be run at certain conditions (assumption) and they guarantee certain functionalities. The execution time of each block is less than the time between 2 triggers.

ARCHITECTURE: CBS Only source nodes can write (fun: write()) Only destination nodes can read (fun: read()) Unknown execution time Atomicity is guaranteed (a function ends before the following one starts) No guarantee in freshness of data (due to execution time) Fun is. New: returns true if there are fresh data � Write add an index (sn) to the data; Reader keeps the index (lsn) of the last read data: if lsn = sn the data is old.

EXAMPLE

INTERMEDIATE LAYER: FFP Architectural similarities with LTTA and semantics close to synchronous Set of sequential processes communicating with finite FIFOs. Processes do NOT block: process has to check whether they can execute (queue is not empty before reading; queue is not full before writing) is. Empty; is. Full; put; get (API similar to Cb. S)

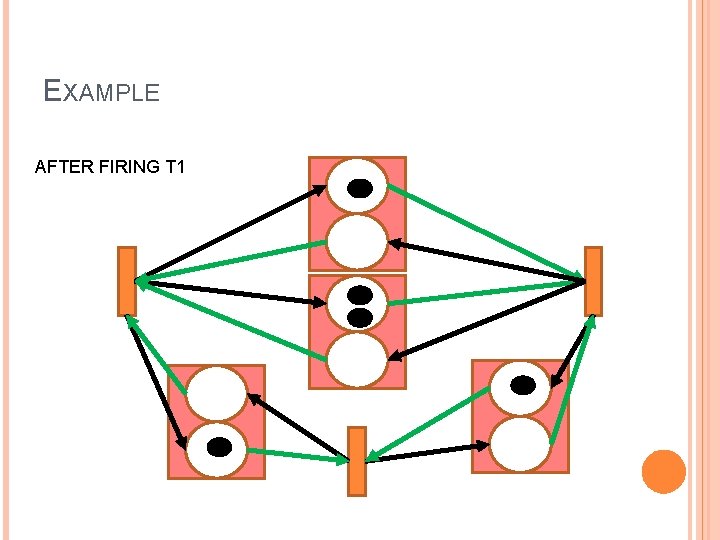
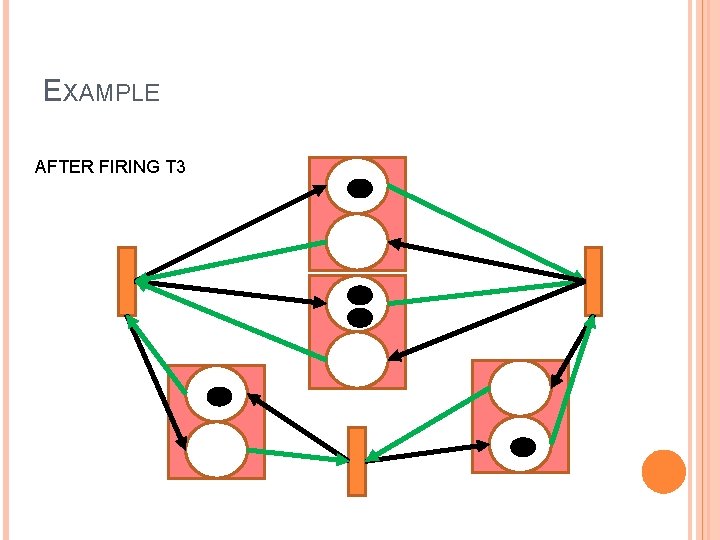
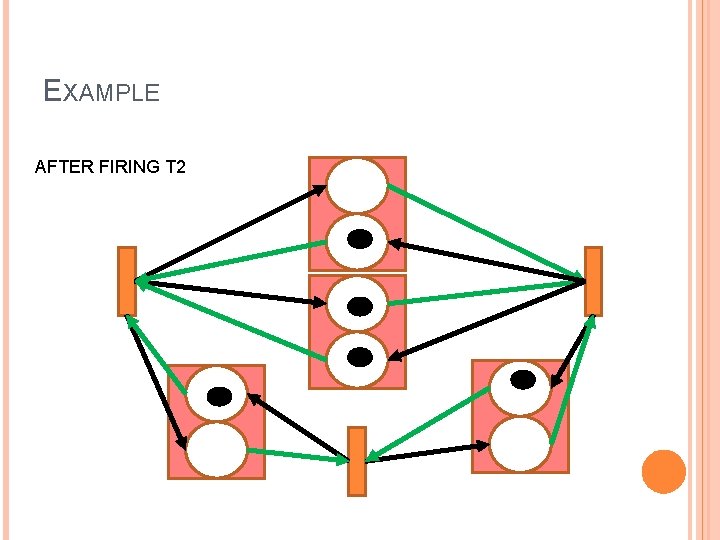
MAPPING SYNC TO FFP Each machine is mapped into a process (UD are not) There is a queue for each link � If the link has a UD the queue is size 2 � If the link has no UD the queue size is 1 At each trigger � IF (all input queues are non-empty and all output queues are non -full) Compute outputs and new state Write outputs to output queues � Else Skip step � End if

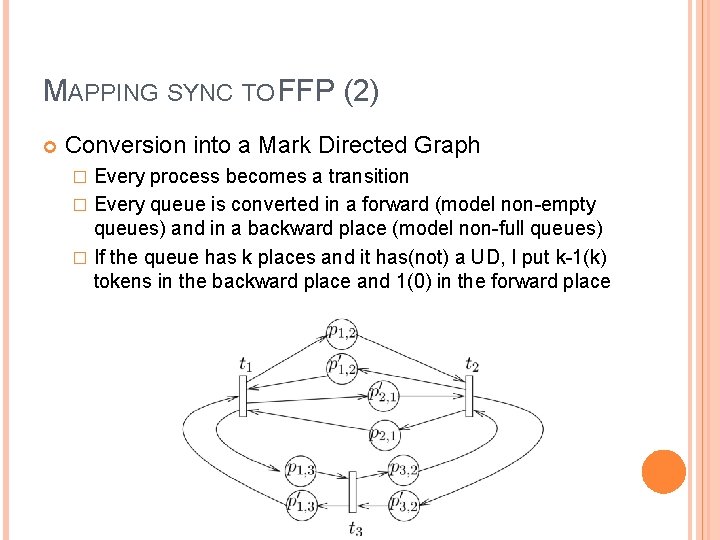
MAPPING SYNC TO FFP (2) Conversion into a Mark Directed Graph Every process becomes a transition � Every queue is converted in a forward (model non-empty queues) and in a backward place (model non-full queues) � If the queue has k places and it has(not) a UD, I put k-1(k) tokens in the backward place and 1(0) in the forward place �

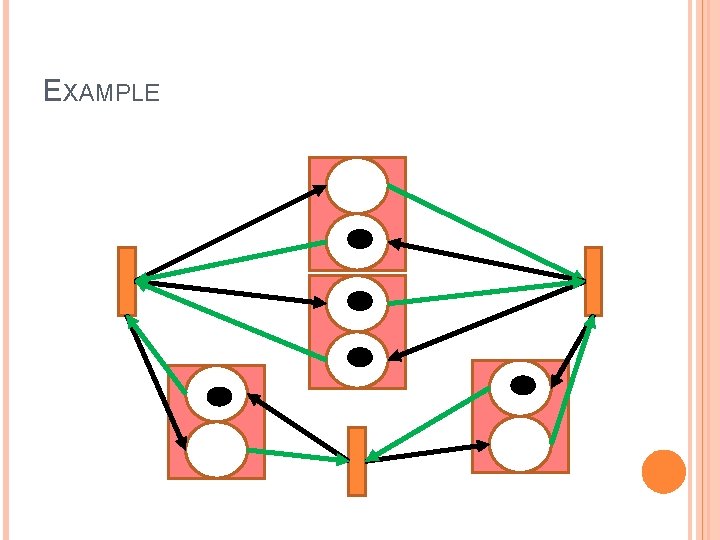
EXAMPLE

EXAMPLE AFTER FIRING T 1

EXAMPLE AFTER FIRING T 3

EXAMPLE AFTER FIRING T 2

MAPPING SYNC TO FFP Theorem: semantic is preserved with queues of size at most 2. � Queue of size 2 if there is a UD; size 1 if there is not. � Step 1: the FFP has no deadlocks (this is true by construction since I put at least one token in each directed circuit) � Step 2: any execution of MDG is one possible execution of the corresponding FFP. Note: check for is. Full is not necessary, because by construction, if inputs are not empty, outputs can’t be full.

MAPPING FFP TOLTTA It is possible to map 1: 1 from FFP to LTTA � FFP API can be implemented on top of LTTA API Semantic is preserved by skipping processes that can’t be fired (either for empty inputs or full outputs)

THROUGHPUT ANALYSIS Need for an estimation of the system throughput (λ): each process either runs or skips for every trigger. Upper bound: clock rate (if globally sync) Is there a lower bound (worst case)?

THROUGHPUT ANALYSIS In RT: Theorem: if the size of a queue is increased, the resulting throughput either increases or remains equal or larger. Need for a symbolical definition of throughput that is independent of the implementation logical-time throughput In LT: The worst-case throughput is

THROUGHPUT ANALYSIS To find the minimum we define a “slow triggering policy”: at each time step, the clock of each process ticks one and only one time and the clocks of disabled processes tick before the clocks of enabled processes Theorem: the throughput of a system that “adopts” the slow triggering policy is the lowest possible � All disabled processes can’t run until the following time step the throughput is minimized

THROUGHPUT ANALYSIS To evaluate the value of λmin we first analyze the associated MDG. � Create a reachability graph (RG) that implements the slow triggering policy it is a graph in which all enabled transitions are fired (i. e. all transitions that are not enabled can’t be fired until the following step) � Determine the lasso starting from M 0 Lasso: a loop in the (RG) that the system travels an infinite number of times (remember: deadlock free)

THROUGHPUT ANALYSIS If L is the length of the lasso, for the process P: The WC throughput is the same for all processes (a lasso is periodic, so all transitions have to be fired the same number of times to return to the starting marking) If Δ is the period of the slowest clock:

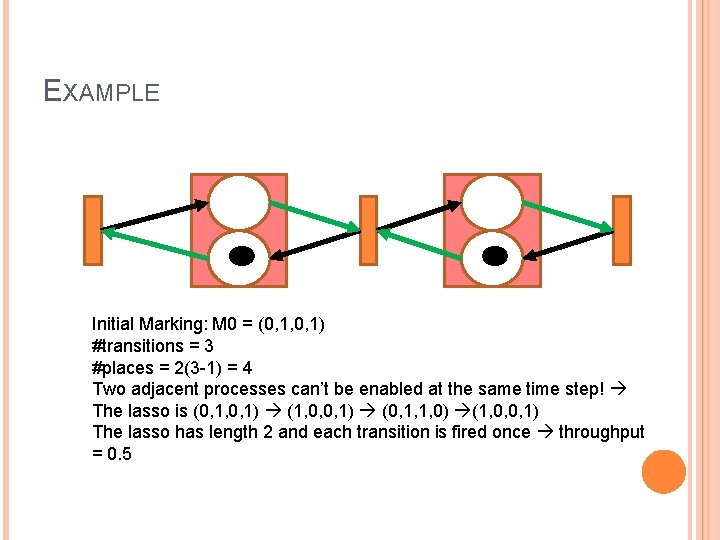
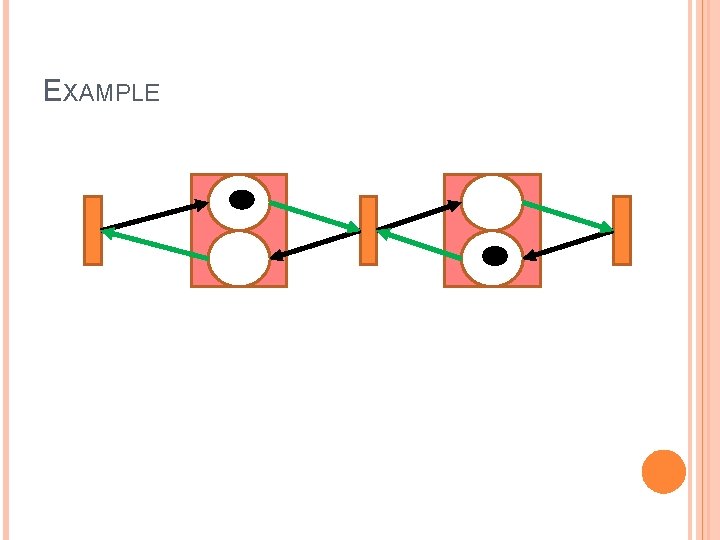
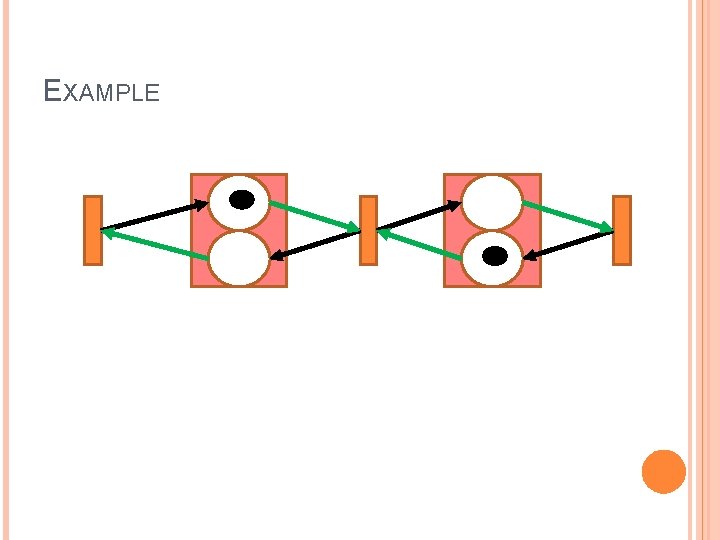
EXAMPLE Initial Marking: M 0 = (0, 1, 0, 1) #transitions = 3 #places = 2(3 -1) = 4 Two adjacent processes can’t be enabled at the same time step! The lasso is (0, 1, 0, 1) (1, 0, 0, 1) (0, 1, 1, 0) (1, 0, 0, 1) The lasso has length 2 and each transition is fired once throughput = 0. 5

EXAMPLE

EXAMPLE

EXAMPLE

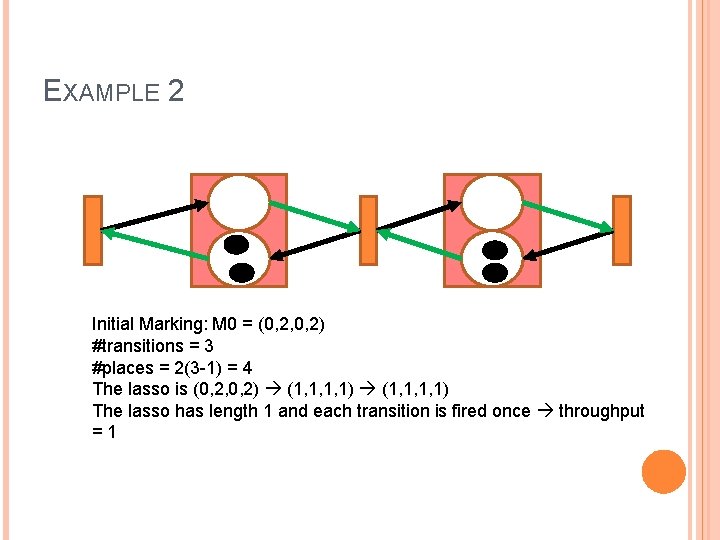
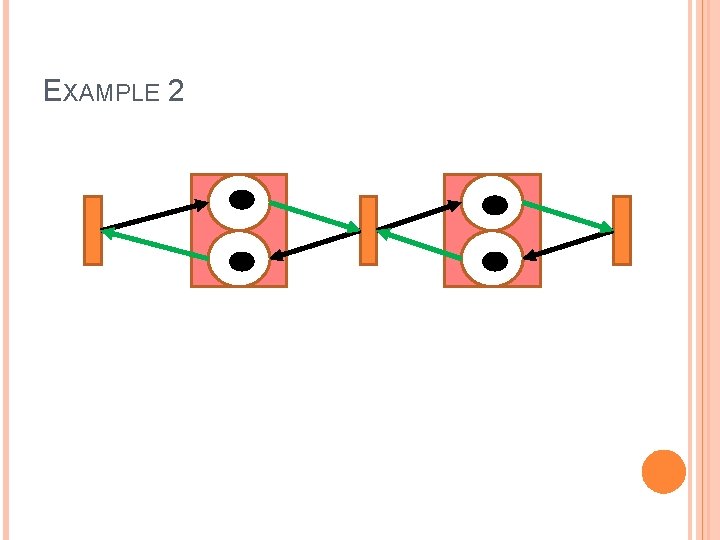
EXAMPLE 2 Initial Marking: M 0 = (0, 2, 0, 2) #transitions = 3 #places = 2(3 -1) = 4 The lasso is (0, 2, 0, 2) (1, 1, 1, 1) The lasso has length 1 and each transition is fired once throughput =1

EXAMPLE 2