Implementing LR Parsers LR parsing tables and building

Implementing LR Parsers LR parsing tables and building LR(0), SLR(1) and LR(1) Parsers Adapted from Notes by Prof. Saman Amarasinghe (MIT)

11 Actions of a Shift-Reduce Parser • Shift to sn – Push input token into the symbol stack – Push sn into state stack – Advance to next input symbol • Reduce – Pop both stacks as many times as the number of symbols on the RHS of rule n – Push LHS of rule n into symbol stack – Lookup [top of the state stack][top of symbol stack] – Push that state (in goto k) into state stack • Accept – End of stream reached and stack only has the start symbol • Reject – End of stream reached but stack has more than the start symbol

53 Building a LR(0) parser engine • Add the special production S’ S $ • Find the items of the CFG • Create the DFA – using closure and goto functions • Build the parse table LR(0) Parser Engine

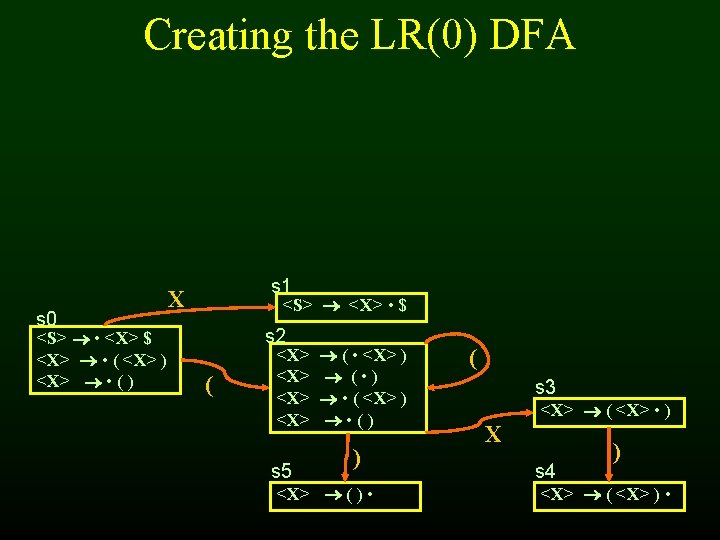
50 Creating the LR(0) parse tables • For each state • Transition to another state using a terminal symbol is a shift to that state (shift to sn) • Transition to another state using a non-terminal is a goto that state (goto sn) • If there is an item A • in the state do a reduction with that production for all terminals (reduce k)

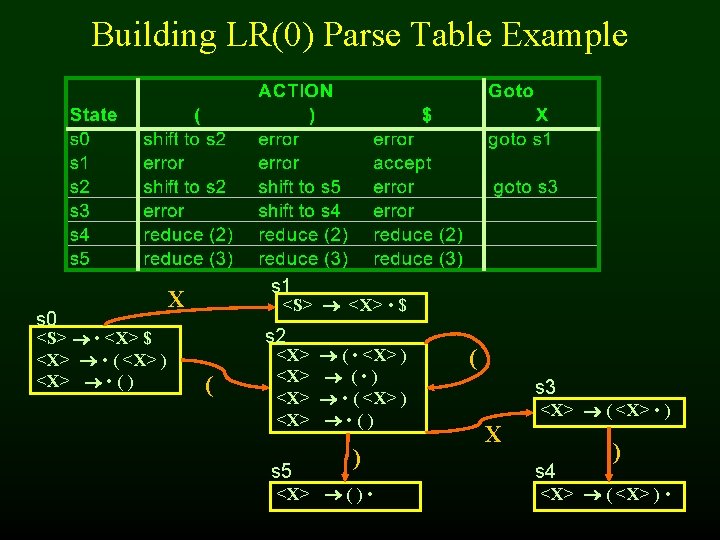
Changing the Language • String of one more left parentheses followed by the same number of right parentheses <S> <X> $ <X> ( <X> ) <X> ( ) • String of zero or more left parentheses followed by the same number of right parentheses <S> <X> $ <X> ( <X> ) <X>

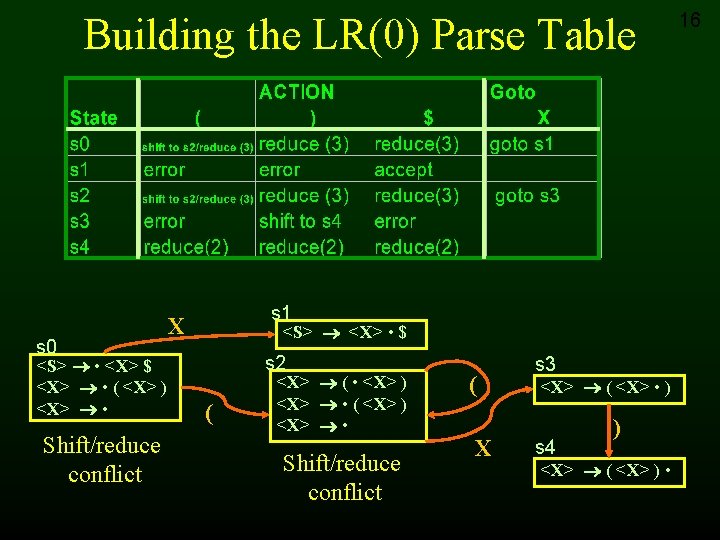
Building the LR(0) Parse Table s 0 <S> • <X> $ <X> • ( <X> ) <X> • Shift/reduce conflict s 1 X <S> <X> • $ s 2 ( <X> ( • <X> ) <X> • ( <X> ) <X> • Shift/reduce conflict ( X s 3 <X> ( <X> • ) s 4 ) <X> ( <X> ) • 16

Idea behind SLR(1) grammars • Many shift/reduce conflicts in LR(0) – an item X • in the current state identifies a reduction – But does not select when to reduce – Thus, have to perform the reduction on all input symbols • Do the reduction only when the input symbol truly follows the reduction – Need to calculate the terminals that can follow a non-terminal symbol

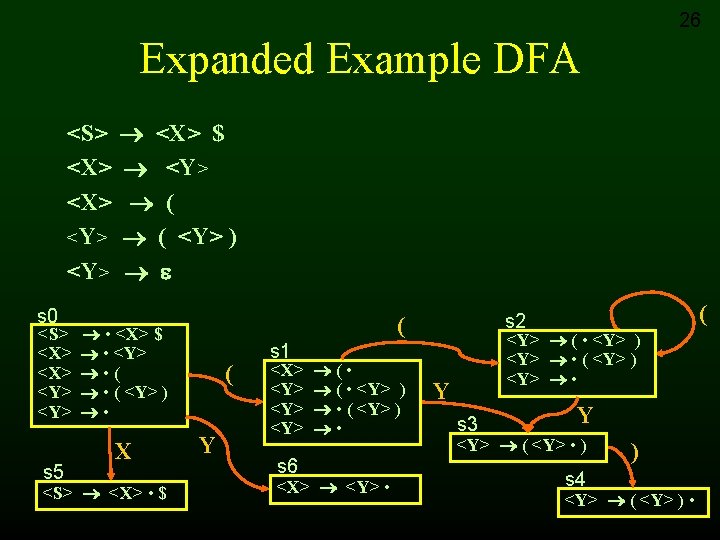
Expanded Example Grammar <S> <X> $ (1) <X> <Y> (2) <X> ( (3) <Y> ( <Y> ) (4) <Y> (5) • Change language to: – Zero or more open parentheses followed by matching # of close parentheses – or a single open parenthesis

31 LR(1) Items • Items will keep info on – production – right-hand-side position (the dot) – look ahead symbol • LR(1) item is of the form [A • – A is a production – The dot in A • denotes the position – a is a terminal or the end marker ($) • For the item [A • a] – a is the next symbol after A in the string i. e. there exist a derivation S A a a]

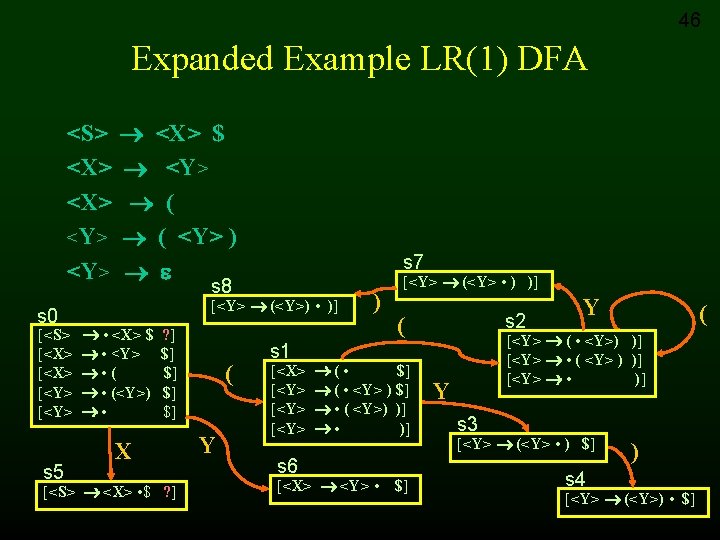
LR(1) 52 s 7 SLR(1) s 7 … s 8 => similar to s 3…s 4 except for “reduce” column.

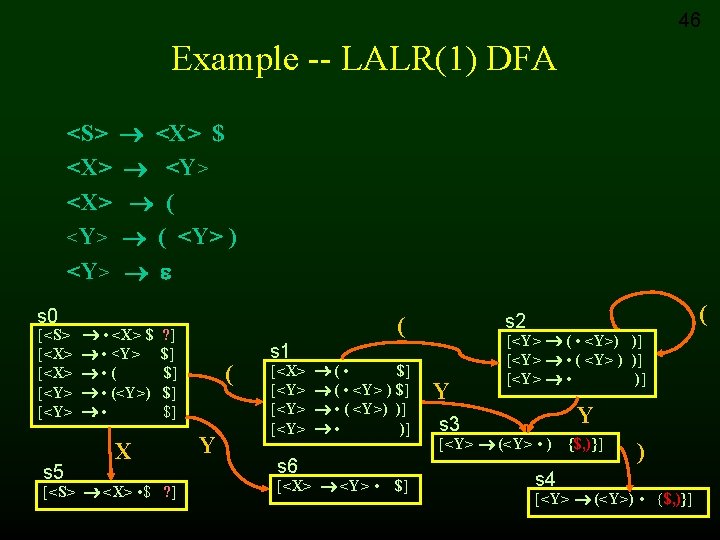
LALR(1) 52 LR(1) reduce(4) s 7 … s 8 =>

SLR(1) LALR(1) 52 reduce(4)

A Hierarchy of Grammar Classes

LR Languages • The set of LR languages are independent of the lookahead distance k. • For all the languages with SLR(1), LALR(1) and LR(1) grammars we looked at, we could have found an LR(0) grammar!!! • This grammar may not be natural however.

LR Languages • Given any LR(k) grammar Gk, if L(Gk) is prefix-free, then there exists an (equivalent) LR(0) grammar G 0 such that L(Gk) = L(G 0) – A language L is prefix-free iff [x in L and xy in L implies y is e]. – A language can be made prefix-free by concatenating a special end-marker to each string in the language.

LR vs LL In general, LL(k) grammars are LR(k) grammars, for any k.

LR(0) vs LL(k) • The following LR(0) grammar (with left recursion) is not LL(1). S S 0 | 0 – The following LR(0) grammar (with left recursion) is not LL(k), for any k. S S 0 | S 1 | 0 | 1 • The following LL(1) grammar is not LR(0). S Z$ Z a. Z | e

Not LR(k) for an k • The following regular grammar (with left recursion) is not LR(k), for any k. S Cc | Bb C Ca | a B Ba | a

SLR(1) vs LL(k) • The following SLR(1) grammar (and hence, LR(1) grammar) requiring left factoring is not LL(k), for any k. E T+E | T T x *T | x

LL(1) vs SLR(1) • The following grammar is LL(1), but not SLR(1). S 1 X | 2 Ag X Af | Bg A 3|e B 4|e

LL(1) vs LALR(1) • The following grammar is LL(1), but not LALR(1). S a. F | b. G F Xc | Yd X IA A e Xd | Yc Y IB I e G B e