Implementing a Sorted List as a Linked Structure

Implementing a Sorted List as a Linked Structure CS 308 – Data Structures

Sorted. List Class Specification template <class Item. Type> struct Node. Type; private: int length; Node. Type<Item. Type>* list. Data; Node. Type<Item. Type>* current. Pos; }; template<class Item. Type> class Sorted. Type { public: Sorted. Type(); ~Sorted. Type(); void Make. Empty(); bool Is. Full() const; int Length. Is() const; void Retrieve. Item(Item. Type&, bool&); void Insert. Item(Item. Type); void Delete. Item(Item. Type); void Reset. List(); bool Is. Last. Item() const; void Get. Next. Item(Item. Type&);

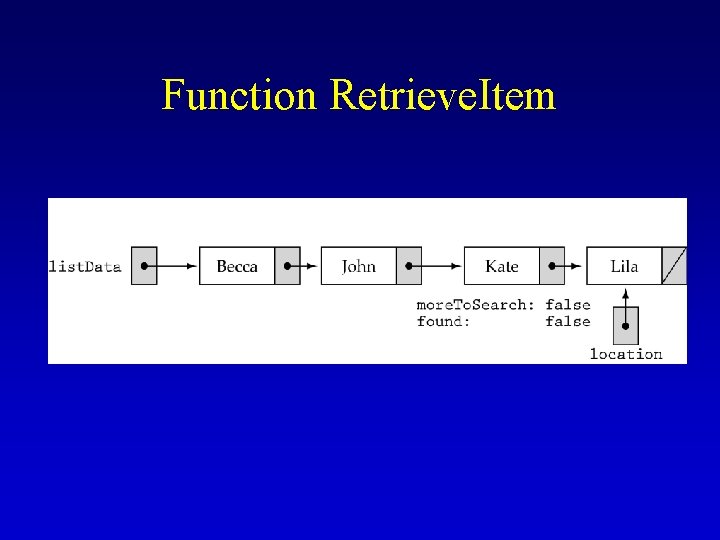
Function Retrieve. Item

Function Retrieve. Item (cont. ) template<class Item. Type> void Sorted. Type<Item. Type>: : Retrieve. Item(Item. Type& item, bool& found) { Node. Type<Item. Type>* location; location = list. Data; found = false; while( (location != NULL) && !found) { if (location->info < item) location = location->next; else if (location->info == item) { found = true; item = location->info; } } } else location = NULL; // no reason to continue

Can we use Binary Search with linked lists?

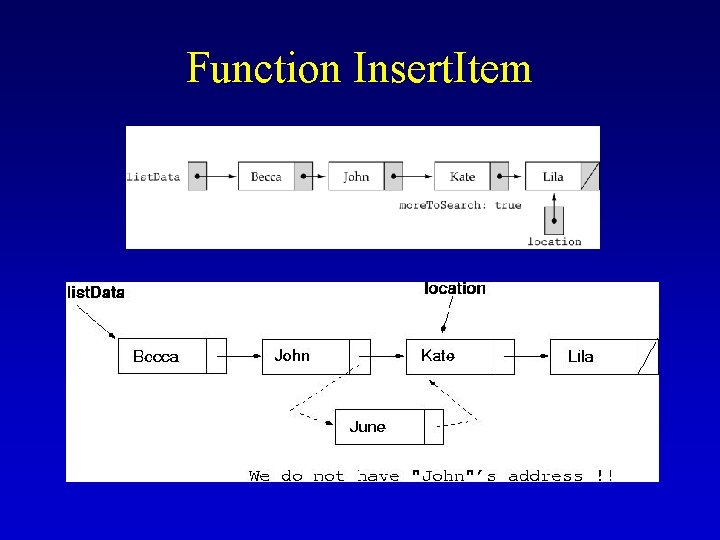
Function Insert. Item

Function Insert. Item (cont. ) • Can we compare one item ahead? ? (like in • the unsorted list case? ) In general, we must keep track of the previous pointer, as well as the current pointer.

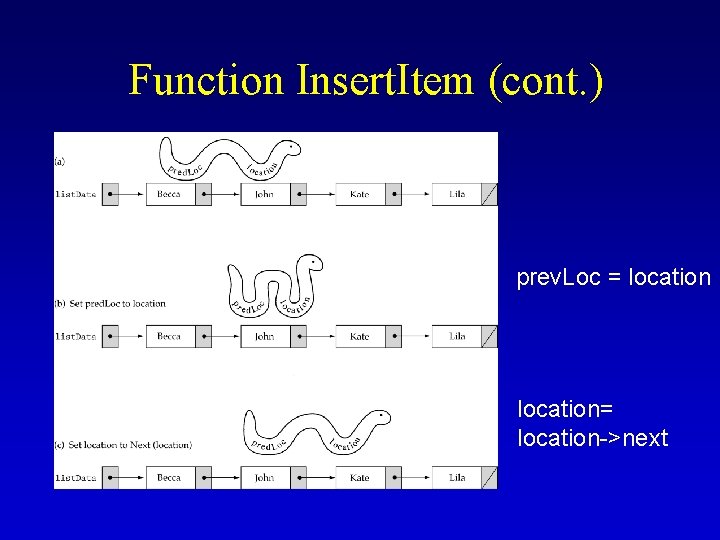
Function Insert. Item (cont. ) prev. Loc = location= location->next

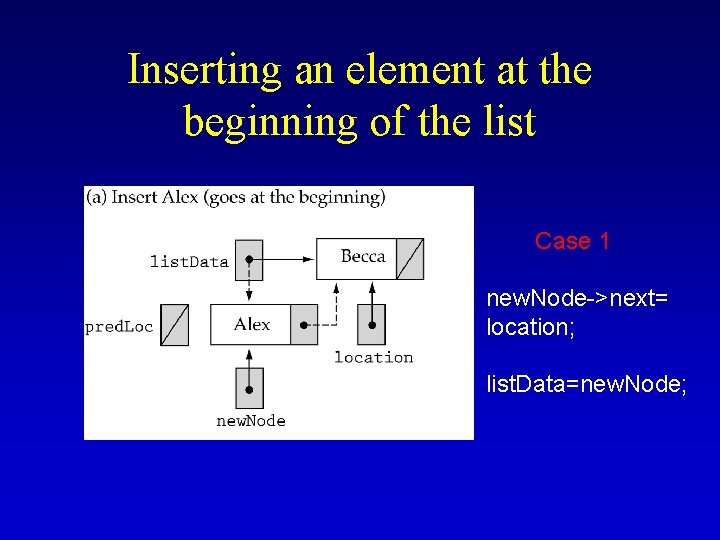
Inserting an element at the beginning of the list Case 1 new. Node->next= location; list. Data=new. Node;

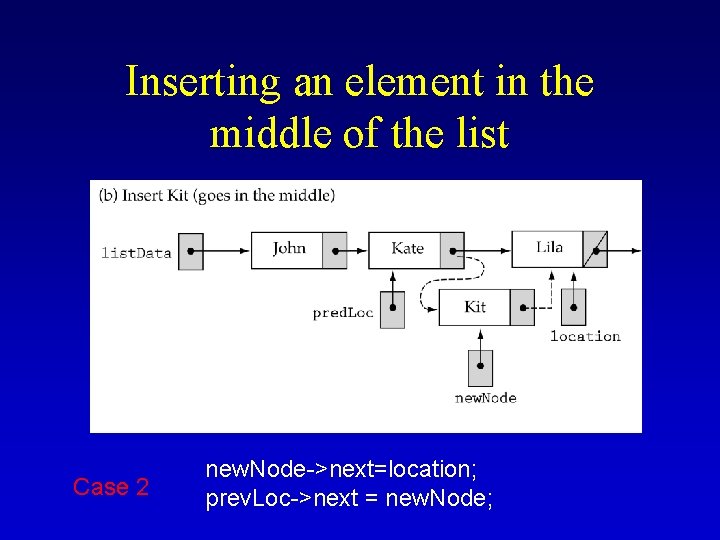
Inserting an element in the middle of the list Case 2 new. Node->next=location; prev. Loc->next = new. Node;

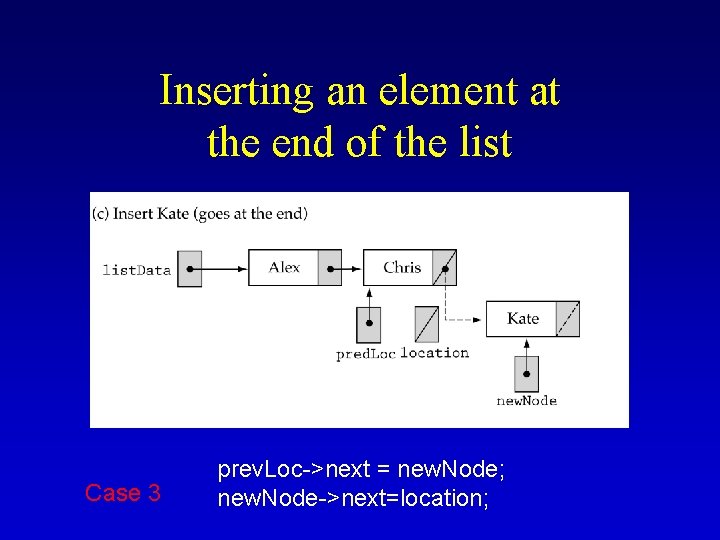
Inserting an element at the end of the list Case 3 prev. Loc->next = new. Node; new. Node->next=location;

Inserting into an empty list Case 4 list. Data=new. Node; new. Node->next=location;

Function Insert. Item (cont. ) template <class Item. Type> void Sorted. Type<Item. Type>: : Insert. Item(Item. Type new. Item) { Node. Type<Item. Type>* new. Node; Node. Type<Item. Type>* pred. Loc; Node. Type<Item. Type>* location; bool stop; stop = false; location = list. Data; pred. Loc = NULL; while( location != NULL && !stop) { if (location->info < new. Item) { pred. Loc = location; location = location->next; } } else stop = true;

Function Insert. Item (cont. ) new. Node = new Node. Type<Item. Type>; new. Node->info = new. Item; if (pred. Loc == NULL) { new. Node->next = list. Data; cases (1) and (4) list. Data = new. Node; } else { new. Node->next = location; pred. Loc->next = new. Node; cases (2) and (3) } length++; }

Function Delete. Item • The Delete. Item we wrote for unsorted lists • works for sorted lists as well Another possibility is to write a new Delete. Item based on the following cases

Deleting the only element in the list

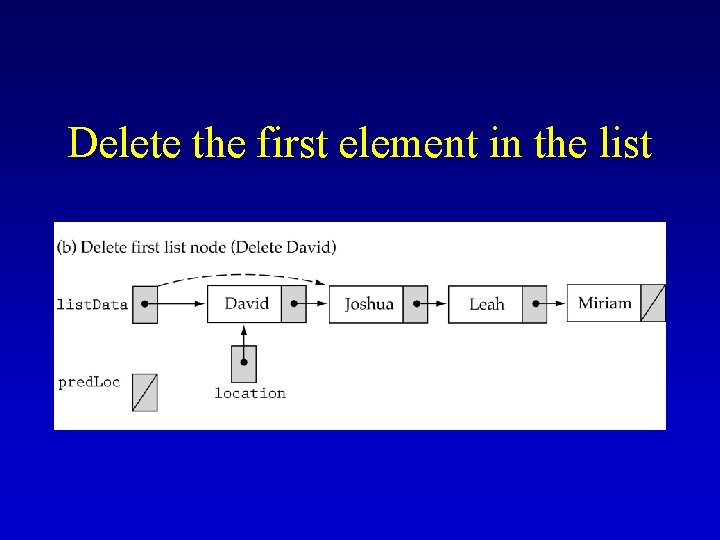
Delete the first element in the list

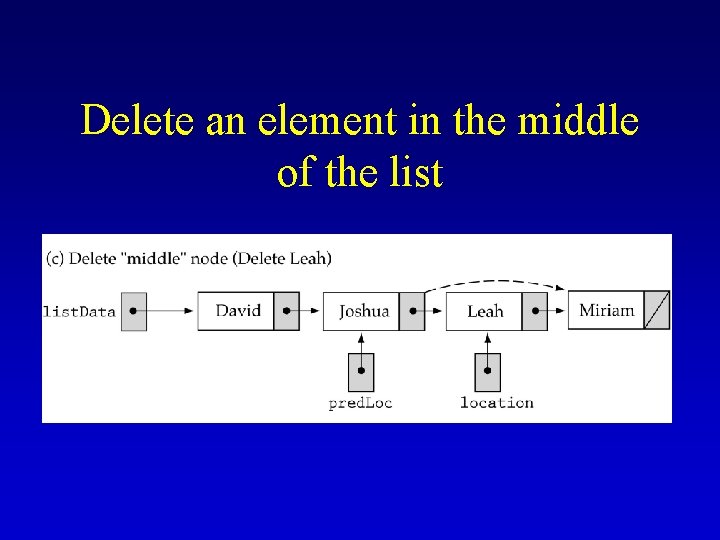
Delete an element in the middle of the list

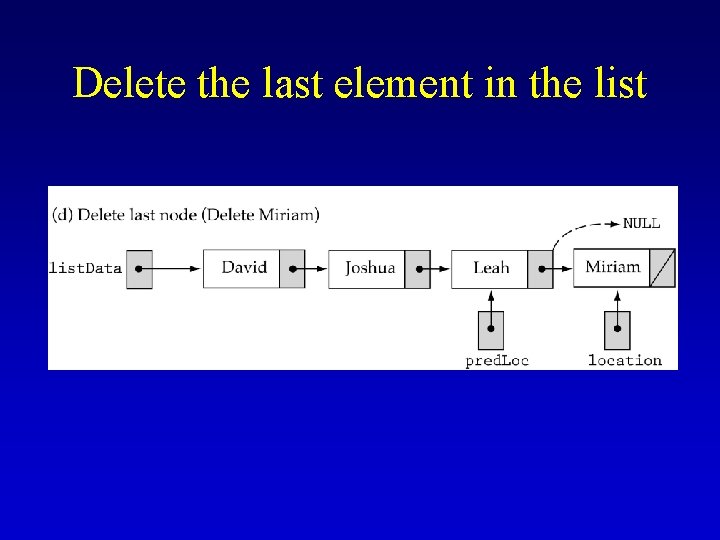
Delete the last element in the list

Other Sorted. List functions • Same as in the case of Unsorted. List class

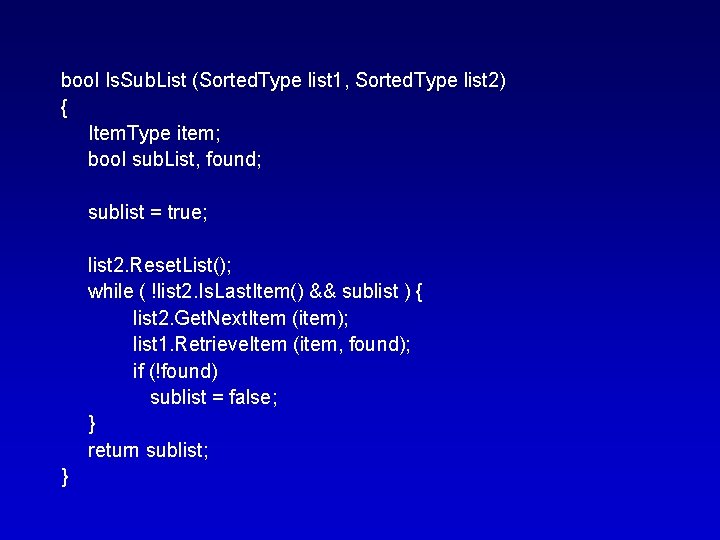
Write a client function that takes two lists (unsorted or sorted) and returns a Boolean indicating whether the second list is a sublist of the first. (i. e. , the first list contains all the elements of the second list but may also contain other elements).

bool Is. Sub. List (Sorted. Type list 1, Sorted. Type list 2) { Item. Type item; bool sub. List, found; sublist = true; list 2. Reset. List(); while ( !list 2. Is. Last. Item() && sublist ) { list 2. Get. Next. Item (item); list 1. Retrieve. Item (item, found); if (!found) sublist = false; } return sublist; }

Write a member function that returns a pointer to the minimum node (i. e. the node storing the smallest value) of an unsorted list. Precondition: list is not empty. How would you implement the same function if the list was sorted? (assume that the elements in a sorted list are sorted in increasing order).

Node. Type<Item. Type>* Unsorted. Type<Item. Type>: : Min. Node() { Node. Type<Item. Type * location, *temp. Location; Item. Type min. Item; min. Item = list. Data->info; temp. Location = list. Data; location = list. Data; while (location->next != NULL) { location = location->next; if (location->info < min. Item) { min. Item=location->info; temp. Location=location; } } return temp. Location; } If the list is sorted, then you just need to return “list. Data” (pointer to the first element).

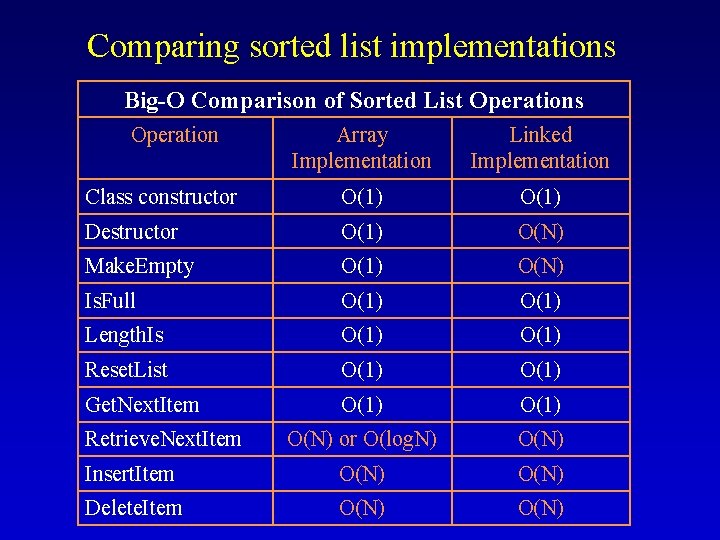
Comparing sorted list implementations Big-O Comparison of Sorted List Operations Operation Array Implementation Linked Implementation Class constructor O(1) Destructor O(1) O(N) Make. Empty O(1) O(N) Is. Full O(1) Length. Is O(1) Reset. List O(1) Get. Next. Item O(1) O(N) or O(log. N) O(N) Insert. Item O(N) Delete. Item O(N) Retrieve. Next. Item

Exercises • 9, 15 - 18