Implementing a BNF Grammar Example design of a

Implementing a BNF Grammar Example design of a data structure 05 -Mar-21

Form of BNF rules n n n n n <BNF rule> : : = <nonterminal> ": : =" <definitions> <nonterminal> : : = "<" <words> ">" <terminal> : : = <word> | <punctuation mark> | ' " ' <any chars> ' " ' <words> : : = <word> | <words> <word> : : = <letter> | <word> <digit> <definitions> : : = <definition> | <definitions> "|" <definition> : : = <empty> | <term> | <definition> <term> <empty> : : = <terminal> | <nonterminal> Not defined here (but you know what they are) : <letter>, <digit>, <punctuation mark>, <any chars> (any printable nonalphabetic character except double quote)

Notes on terminology n n n n A grammar typically has a “top level” element A string is a “sentential form” if it satisfies the syntax of the top level element A string is a “sentence” if it is a sentential form and is composed entirely of terminals A string “belongs to” a grammar if it satisfies the rules of that grammar BNF was developed by John Backus and Peter Naur, computer scientists, in the 1950 s Context-free grammars were independently developed in 1956 by the linguist, Noam Chomsky, to describe human languages BNF and context-free grammars use slightly different notation, but are completely equivalent

Uses of a grammar n A BNF grammar can be used in two ways: n To generate strings belonging to the grammar n n To do this: n start with a string containing a nonterminal; while there are still nonterminals in the string { replace a nonterminal with one of its definitions } To recognize strings belonging to the grammar n n This is the way programs are compiled--a program is a string belonging to the grammar that defines the language Recognition is much harder than generation

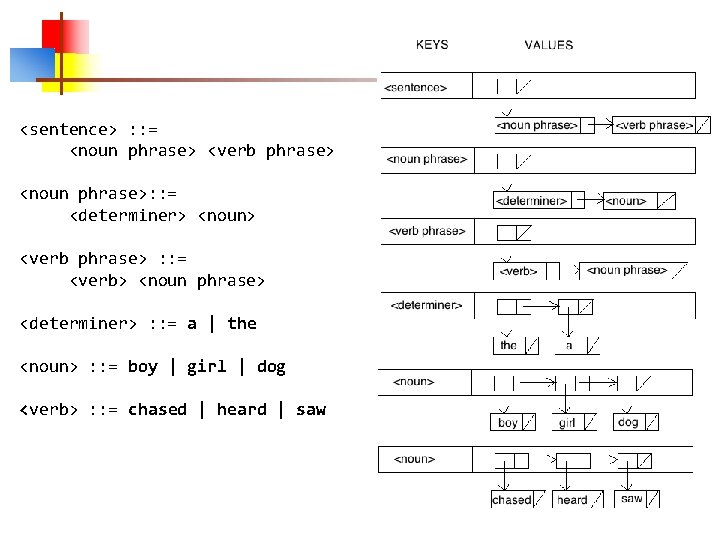
Sample generation n n <sentence> : : = <noun phrase> <verb phrase> <noun phrase>: : = <determiner> <noun> <verb phrase> : : = <verb> <noun phrase> <determiner> : : = a | the <noun> : : = boy | girl | dog <verb> : : = chased | heard | saw <sentence> (I’m underlining the nonterminal that I’m about to expand) <noun phrase> <verb phrase> (The just-expanded part is in blue) <determiner> <noun> <verb phrase> the <noun> <verb> <noun phrase> the boy <verb> <determiner> <noun> the boy chased <determiner> girl the boy chased the girl

Generating sentences n n I want to write a program that reads in a grammar, stores it in some appropriate data structure, then generates random sentences belonging to that grammar I need to decide: n n n How to store the grammar What operations to provide on the grammar These decisions are intertwined! n How I store the grammar determines what operations are easy and efficient (and even possible!)

Philosophy n “Bad programmers worry about the code. Good programmers worry about data structures and their relationships. ” --Linus Torvalds, creator of Linux n “Smart data structures and dumb code works a lot better than the other way around. ” --Eric Raymond, in The Cathedral and the Bazaar

Data structures for sentence generation n BNF, and sentence generation using BNF, are defined in terms of string manipulation n n Since we want to repeatedly look up nonterminals to find their definitions, a map from nonterminals (keys) to definitions (values) is the obvious thing to do n n We could write a sentence generation program using only strings, but it would be unnecessarily difficult For speed, we should use a Hash. Map; but to print the nonterminals in alphabetical order, we should use a Tree. Map Since a nonterminal may have an arbitrary number of definitions, those various definitions can be stored as a set or a list n Lists are somewhat easier to work with; in particular, it’s easier to choose a random value from an Array. List n Each individual definition is some number of terminals and/or nonterminal, in a specific order, so a list is most appropriate So to store our BNF, we use a Tree. Map<String, <Array. List<String>>> n Notice that this structure would not be useful for recognizing sentences n

<sentence> : : = <noun phrase> <verb phrase> <noun phrase>: : = <determiner> <noun> <verb phrase> : : = <verb> <noun phrase> <determiner> : : = a | the <noun> : : = boy | girl | dog <verb> : : = chased | heard | saw

Data structures for sentential forms n n In addition to storing the BNF grammar, we need a data structure to hold sentential forms. Recall that: n n So as we develop <sentence> → <noun phrase> <verb phrase> → <determiner> <noun> <verb phrase> → … → the boy chased the girl, we need a data structure that allows us to easily change each of these sentential forms into the next Two possible structures seem especially appropriate: n n n A grammar typically has a “top level” element A string is a “sentential form” if it satisfies the syntax of the top level element A tree, with <sentence> as the root A list of terminals and nonterminals Considering the operations required (expanding nonterminals, printing the final result), both of these seem about equally easy

Development approaches n Bad approach: Design a general representation for grammars and a complete set of operations on them n n n Good approach: Decide the operations you need for this program, and design a representation for grammars that supports these operations n n n Actually, this is a good approach if you are writing a general-purpose package for general use--for example, for inclusion in the Java API Otherwise, it just makes your program much more complex It’s a nice bonus if the design can later be extended for other purposes Remember the Extreme Programming slogan YAGNI: “You ain’t gonna need it. ” Our program will generate sentences, not recognize them!

Requirements and constraints n We need to read the grammar in n We need to look up the definitions of nonterminals n n But we don’t need to modify it later Any tools for building the grammar structure can be private We need this because we will need to replace each nonterminal with one of its definitions We need to know the top level element of the grammar n n But we can just assume that we know what it is For example, we can insist that the top-level element be <sentence>

First cut n n public class Grammar implements Iterable List<String> rule; // a single alternative for a nonterminal List<String>> definition; // all the rules for one nonterminal Map<String, List<String>>> grammar; // rules for all the nonterminals n n n n public public Grammar() { grammar = new Tree. Map<String, List<String>>(); } void add. Rule(String rule) throws Illegal. Argument. Exception List<String>> get. Definition(String nonterminal) List<String> get. One. Rule(String nonterminal) // random choice Iterator iterator() void print()

First cut: Evaluation n Advantages n n Small, easily learned interface Just one class Can be made to work Disadvantages n n n As designed, <foo> : : = bar | baz is two rules, requiring two calls to add. Rule; hence requires caller to do some of the parsing, to separate out the left-hand side Requires some fairly complicated use of generics Array. List implements List (hence is a List), but consider: List<String>> definition = make. List(); n This statement is legal if make. List() returns an Array. List<String>> n It is not legal if make. List() returns an Array. List<String>>

Second cut: Overview n n We can eliminate the compound generics by using more than one class public class Grammar implements Iterable Map<String, Definitions> grammar; // all the rules public class Definitions List<Rule> definition; public class Rule String lhs; // the definiendum List<String> rhs; // the definiens

Second cut: More detail n n n public class Grammar implements Iterable Map<String, Definition> grammar; // rules for all the nonterminals public Grammar() { grammar = new Tree. Map<String, Definition>(); } // constructor public void add. Rule(String rule) throws Illegal. Argument. Exception public Definition get. Definition(String nonterminal) public Iterator iterator() public void print() public class Definition List<Rule> definition; // all definitions for some unspecified nonterminal Definition() // constructor void add. Rule(Rule rule) Rule get. One. Rule() public String to. String() public class Rule String lhs; // the definiendum List<String> rhs; // the definiens Rule(String text) // constructor public String get. Left. Hand. Side() public List<String> get. Right. Hand. Side() public String to. String()

Second cut: Evaluation n Advantages: n n Simplifies use of generics Disadvantages: n n Many more methods Definitions are “unattached” from nonterminal being defined n n This makes it easier to parse definitions Seems a bit unnatural Need to pass the tokenizer around as an additional argument Doesn’t help with the problem that the caller still has to separate out the definiendum from the definiens

Third (very brief) cut n Definition and Rule are basically both just lists of strings n n Why not just have them implement List? Methods to implement: n public public public public public public boolean add(Object o) void add(int index, Object element) boolean add. All(Collection c) boolean add. All(int index, Collection c) void clear() boolean contains(Object o) boolean contains. All(Collection c) Object get(int index) int index. Of(Object o) boolean is. Empty() Iterator iterator() int last. Index. Of(Object o) List. Iterator list. Iterator(int index) boolean remove(Object o) Object remove(int index) boolean remove. All(Collection c) boolean retain. All(Collection c) Object set(int index, Object element) int size() List sub. List(int from. Index, int to. Index) Object[] to. Array(Object[] a)

Fourth cut, not quite as brief n The class Abstract. List “provides a skeletal implementation of the List interface. . . the programmer needs only to extend this class and provide implementations for the get(int index) and size() methods. ” n I tried this, but. . . n n n If I don’t know how Abstract. List is implemented, how can I write these methods? No book or API class that I looked at provided any clues I may be missing something, but it looks like the only thing to do is to look at the source code for some of Java’s classes (like Array. List) to see how they do it n Doable, but too much work!

Letting go of a constraint n n n It is good practice to use a more general class or interface if you don’t need the services of a more specific class In this problem, I want to use lists, but I don’t care whether they are Array. Lists, or Linked. Lists, or something else Hence, I generally prefer declarations like List<String> list = new Array. List<String>(); In this case, however, trying to do this just seems to be the cause of many of the problems What happens if I just make all lists Array. Lists?

Fifth (and final) cut n n n public class Grammar n Map<String, Definitions> grammar; // rules for all the nonterminals n public Grammar() { grammar = new Tree. Map<String, List. Of. Definitions >(); } n public void add. Rule(String rule) throws Illegal. Argument. Exception n public List. Of. Definitions get. Definitions(String nonterminal) n public void print() n public static boolean is. Nonterminal(String s) { return s. starts. With("<") && s. ends. With(">") && s. length() > 2; } n private void add. To. Grammar(String lhs, Single. Definition definition) public class List. Of. Definitions extends Array. List<Single. Definition> n @Override public String to. String() public class Single. Definition extends Array. List<String> n @Override public String to. String()

Explanation I of final BNF API n n Example: <unsigned integer> : : = <digit> | <unsigned integer> <digit> The above is a rule n n <unsigned integer> is the definiendum (the thing being defined) <digit> is a single definition of <unsigned integer> <digit> is another single definition of <unsigned integer> So, n n There is a Single. Definition consisting of the Array. List [ "<digit>" ] Another Single. Definition consists of the Array. List [ "<unsigned integer>", "<digit>" ] A List. Of. Definitions object is a list of single definitions, in this case: [ [ "<digit>" ], [ "<unsigned integer>", "<digit>" ] ] A Grammar maps nonterminals onto their definitions; thus, a grammar containing the above rule would include the mapping: "<unsigned integer>" [ [ "<digit>" ], [ "<unsigned integer>", "<digit>" ] ]

Explanation II of final BNF API n n A Grammar is a set of mappings from definienda (nonterminals) to definitions, along with some operations on that set of definitions You can add. Rule(String rule) to a Grammar n n The rule is parsed, and an entry made in the map Definitions for a nonterminal may be together, as in the above example, or separate: n n <unsigned integer> : : = <digit> <unsigned integer> : : = <unsigned integer> <digit> You can get the List. Of. Definitions for a given nonterminal You can print the complete Grammar

Final version: Evaluation n Advantages: n n n Grammar has one constructor and three public methods List. Of. Definitions and Single. Definition are just Array. Lists, so there are no new methods to learn All rule parsing is consolidated into a single public method, add. Rule(String rule) I was able to come up with more meaningful names for classes Disadvantages: n User has to do a bit more list manipulation; in particular, choosing a random element from a list n This doesn’t seem like an appropriate thing to have in a grammar, anyway

Morals n n “Weeks of programming can save you hours of planning. ” The mistake most programmers make is to use the first design that comes to mind n n n Much as we would like to pretend otherwise, programming is an iterative process--we design, then try to implement, then change the design, then try to implement. . TDD (Test-Driven Development) is a “lightweight” (low cost) way to try out a design n This usually can be made to work, but it’s seldom optimal For example, in my first design, I discovered how difficult it was to write tests that used the complex generics Consequently, I never even tried to implement this first design Morals to take home: n n Be flexible; try out more than one design Do TDD

Aside: Tokenizing the input grammar n I wrote a Bnf. Tokenizer class that returns every token as a String n n Nonterminals keep their angle brackets, and may be multiword Double-quoted strings are returned as a single token (minus the double quotes) : : = and | are returned as single tokens Bnf. Tokenizer uses Stream. Tokenizer n n It provides two constructors, Bnf. Tokenizer() and Bnf. Tokenizer(String text) And two methods, void tokenize(text) and String next. Token()

The End