Implementation of Graphs Identification of Classes and Interfaces

Implementation of Graphs • Identification of Classes and Interfaces • Concrete Implementations for Graph • Review Questions.

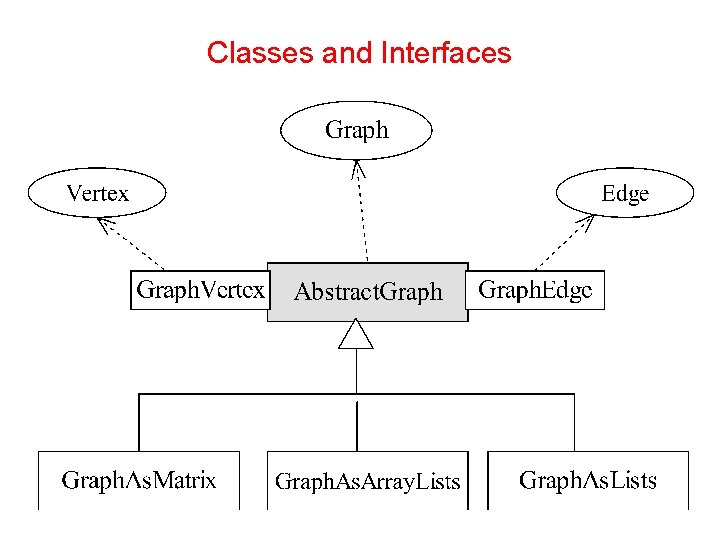
Identification of Classes • A graph contains vertices and edges. • We can identify three kinds of objects: vertices, edges, and graphs. • Accordingly, we define three interfaces: – Vertex – Edge – Graph • A graph can be represented in different ways (we know three of them). Accordinglg, we use the following six classes – Abstract. Graph (having the following two inner classes) • Graph. Vertex • Graph. Edge – Graph. As. Matrix – Graph. As. Array. Lists – Graph. As. Lists

Classes and Interfaces

The Vertex Interface • Each vertex must be distinguishable from other vertices. Thus, each vertex should have a unique label. • Some applications require vertex-weighted graphs. • A vertex type object belongs to exactly one graph. It is neither independent nor shared between two graphs. Otherwise the get. Incident. Edges(), and other methods will not make sense. public interface Vertex extends Comparable { public String get. Label(); public Comparable get. Weight(); public Iterator get. Incident. Edges(); public Iterator get. Emanating. Edges(); public Iterator get. Predecessors(); public Iterator get. Successors(); }

The Edge Interface • An edge in a directed graph is an ordered pair of vertices; while in an undirected graph it is a set of two vertices. • We use the same class for both--the context determines whether it is directed or undirected. • Some edges may have weight public interface Edge extends Comparable { public abstract Vertex get. From. Vertex(); public abstract Vertex get. To. Vertex(); public abstract Comparable get. Weight(); public abstract boolean is. Directed(); public abstract Vertex get. Mate(Vertex vertex); }

The Graph Interface • It represents both directed and undirected graphs. public interface Graph { public int get. Number. Of. Edges(); public int get. Number. Of. Vertices(); public Iterator get. Edges(); } public void add. Vertex(String label); void add. Vertex(String label, Comparable weight); Vertex get. Vertex(String label); int get. Index(Vertex v); // vertices are indexed starting from zero public void add. Edge(String from, String Edge get. Edge(String from, String boolean is. Reachable(String from, public public public boolean is. Directed(); boolean is. Weighted(); boolean is. Connected(); abstract boolean is. Strongly. Connected(); abstract boolean is. Weakly. Connected(); boolean is. Cyclic(); void preorder. Depth. First. Traversal(Visitor visitor, Vertex start); void postorder. Depth. First. Traversal(Visitor visitor, Vertex start); void breadth. First. Traversal(Visitor visitor, Vertex start); abstract int topological. Order. Traversal(Visitor visitor); to); to, Comparable weight); to); String to);

The Abstract. Graph class • The following introduces the Abstract. Graph class. public abstract class Abstract. Graph implements Graph { protected int number. Of. Vertices; protected int number. Of. Edges; protected boolean directed; public Abstract. Graph(boolean directed){ number. Of. Vertices = 0; number. Of. Edges = 0; this. directed = directed; } public int get. Number. Of. Vertices(){return number. Of. Vertices; } public int get. Number. Of. Edges(){return number. Of. Edges; } public void purge() { number. Of. Vertices = 0; implemented in subclasses number. Of. Edges = 0; } public void add. Vertex(String label){add. Vertex(label, null); } public void add. Edge(String from, String to){add. Edge(from, to, null); } public boolean is. Directed() {return directed; }

The Abstract. Graph class- Cont'd public boolean is. Weighted(){ Iterator p = get. Edges(); if(((Edge)p. next()). get. Weight() == null) return false; return true; } public Vertex get. Vertex(String label){ Iterator i = get. Vertices(); while (i. has. Next()){ Vertex v = (Vertex) i. next(); if (v. get. Label(). equals(label)) return v; } return null; } public Edge get. Edge(String from, String to){ Iterator i = get. Edges(); while (i. has. Next()){ Edge e = (Edge) i. next(); if (e. get. From. Vertex(). get. Label(). equals(from) && e. get. To. Vertex(). get. Label(). equals(to)) return e; } return null; }

The Abstract. Graph class- Cont'd public Iterator get. Emanating. Edges(Vertex from) { Iterator i = get. Edges(); My. Linked. List em. Edges = new My. Linked. List(); while (i. has. Next()){ Edge edge = (Edge) i. next(); if (edge. get. From. Vertex(). equals(from)) em. Edges. append(edge); } return em. Edges. iterator(); } public Iterator get. Incident. Edges(Vertex to) { Iterator i = get. Edges(); My. Linked. List in. Edges = new My. Linked. List(); while (i. has. Next()){ Edge edge = (Edge) i. next(); if (edge. get. To. Vertex(). equals(to)) in. Edges. append(edge); } return in. Edges. iterator(); } public int get. Index(Vertex v){ return get. Index(v. get. Label()); } protected abstract int get. Index(String label); Other methods of the Abstract. Graph class will be discussed in coming lectures

The Graph. Vertex class • The Graph. Vertex class is implemented as an inner class: protected final class Graph. Vertex implements Vertex { protected String label; protected Comparable weight; protected Graph. Vertex(String s, Comparable w) { label = s; weight = w; } protected Graph. Vertex(String s) {this(s, null); } public int compare. To(Object obj) { return label. compare. To(((Graph. Vertex)obj). get. Label()); } public Iterator get. Incident. Edges() { return Abstract. Graph. this. get. Incident. Edges(this); } public Iterator get. Predecessors() { return new Iterator() { Iterator edges = get. Incident. Edges(); public boolean has. Next() {return edges. has. Next(); } public Object next() { Edge edge = (Edge)edges. next(); return edge. get. Mate(Graph. Vertex. this); } The get. Emanating. Edges and get. Successors }; } methods are implemented in the same way. }

The Graph. Edge class • The Graph. Edge class is also implemented as an inner class: protected final class Graph. Edge implements Edge { protected Vertex start. Vertex, end. Vertex; protected Comparable weight; protected Graph. Edge(Vertex v 1, Vertex v 2, Comparable w) { start. Vertex = v 1; end. Vertex = v 2; weight = w; } protected Graph. Edge(Vertex v 1, Vertex v 2) {this(v 1, v 2, null); } public Vertex get. From. Vertex() {return start. Vertex; } public Vertex get. To. Vertex() {return end. Vertex; } public Comparable get. Weight() {return weight; } public Vertex get. Mate(Vertex v) { if(v. equals(start. Vertex)) return end. Vertex; if(v. equals(end. Vertex)) return start. Vertex; else throw new Invalid. Operation. Exception("invalid vertex"); } public boolean is. Directed() { return Abstract. Graph. this. Directed(); } // … }

Implementing Graph. As. Matrix (Adjacency Matrix) • The following describes the concrete class, Graph. As. Matrix: public class Graph. As. Matrix extends Abstract. Graph { private int size; private Vertex[] vertices; private Edge[][] edges; public Graph. As. Matrix(int size, boolean directed) { super(directed); this. size = size; vertices = new Graph. Vertex[size]; edges = new Edge[size]; } public void purge() { for (int i=0; i<size; i++){ vertices[i] = null; for (int j=0; j<size; j++) edges[i][j] = null; } super. purge(); } public int get. Index(String label){ for (int i=0; i<number. Of. Vertices; i++) if (vertices[i]. get. Label(). equals(label)) return i; return -1; }

Implementing Graph. As. Matrix - Cont'd public void add. Vertex(String label, Comparable weight){ if (get. Index(label)!=-1) throw new Illegal. Argument. Exception("Duplicate vertex"); if (number. Of. Vertices == size) throw new Illegal. Argument. Exception("Graph is full"); vertices[number. Of. Vertices++] = new Graph. Vertex(label, weight); } public void add. Edge(String from, String to, Comparable weight){ int i = get. Index(from); int j = get. Index(to); if (i==-1 || j==-1) throw new Illegal. Argument. Exception("Vertex not in this graph"); if (i == j) throw new Illegal. Argument. Exception("Loops not supported"); if (edges[i][j] == null){ edges[i][j] = new Graph. Edge(vertices[i], vertices[j], weight); number. Of. Edges++; if (!is. Directed() && edges[j][i]==null){ edges[j][i]=new Graph. Edge(vertices[j], vertices[i], weight); number. Of. Edges++; } } }

Implementing Graph. As. Matrix - Cont'd public Iterator get. Vertices(){ return new Iterator(){ int index = 0; public boolean has. Next(){return index < number. Of. Vertices; } public Object next(){return vertices[index++]; } }; } public Iterator get. Edges() { return new Iterator(){ int count = 0, i=0, j=0; public boolean has. Next(){return count < number. Of. Edges; } public Object next(){ if (count==number. Of. Edges) throw new No. Such. Element. Exception(); while (i<number. Of. Vertices && j<number. Of. Vertices && edges[i][j]==null){ j++; if (j==number. Of. Vertices){j=0; i++; } } Edge r = edges[i][j]; count++; // for next call, adust i and j j++; if (j==number. Of. Vertices){j=0; i++; } return r; } }; }

Implementing Graph. As. Lists (Simple List) • The following describes the concrete class, Graph. As. Lists: public class Graph. As. Lists extends Abstract. Graph { private My. Linked. List list. Of. Vertices, list. Of. Edges; public Graph. As. Lists(boolean directed) { super(directed); list. Of. Vertices = new My. Linked. List(); list. Of. Edges = new My. Linked. List(); } public void purge() { list. Of. Vertices. purge(); list. Of. Edges. purge(); super. purge(); } public int get. Index(String label){ int index = -1; My. Linked. List. Element e = list. Of. Vertices. get. Head(); while (e != null){ index++; Vertex v = (Vertex) e. get. Data(); if (label. equals(v. get. Label())) return index; e = e. get. Next(); } return -1; }

Implementing Graph. As. Lists – Cont’d public void add. Vertex(String label, Comparable weight){ if (get. Index(label)!=-1) throw new Illegal. Argument. Exception("Duplicate vertex"); list. Of. Vertices. append(new Graph. Vertex(label, weight)); number. Of. Vertices++; } public void add. Edge(String from, String to, Comparable weight){ Vertex from. Vertex = get. Vertex(from); Vertex to. Vertex = get. Vertex(to); if (from. Vertex==null || to. Vertex==null) throw new Illegal. Argument. Exception("Vertex not in this graph"); if (from. Vertex == to. Vertex) throw new Illegal. Argument. Exception("Loops not supported"); if (get. Edge(from, to)==null){ list. Of. Edges. append(new Graph. Edge(from. Vertex, to. Vertex, weight)); number. Of. Edges++; if (!is. Directed() && get. Edge(to, from)==null){ list. Of. Edges. append(new Graph. Edge(to. Vertex, from. Vertex, weight)); number. Of. Edges++; } } } public Iterator get. Edges() {return list. Of. Edges. iterator(); } public Iterator get. Vertices(){return list. Of. Vertices. iterator(); }

Implementing Graph. As. Array. Lists (Adjacency List) • The following describes implementation of graph as Adjacency List public class Graph. As. Array. Lists extends Abstract. Graph { private int size; private Vertex[] vertices; private My. Linked. List[] edges; public Graph. As. Array. Lists(int size, boolean directed) { super(directed); this. size = size; vertices = new Graph. Vertex[size]; edges = new My. Linked. List[size]; for (int i=0; i<size; i++) edges[i] = new My. Linked. List(); } // These methods are similar to those in Graph. As. Matrix class public int get. Index(String label) public void add. Vertex(String label, Comparable weight) public Iterator get. Vertices() // These methods will be implemented in the lab public void purge() public void add. Edge(String from, String to, Comparable weight) public Iterator get. Edges() }

Simple Programming Questions on Graphs 1. Write an instance method public Edge min. Weight. Edge() in one of the concrete Graph classes that returns the minimum-weight edge. Your method must throw an appropriate exception if the graph is not weighted. Your method must not use any Iterator. 2. Write an instance method public int count. Special. Edges() of Abstract. Graph that counts the number of edges in the invoking object that have starting vertex greater than ending vertex (based on compare. To method).

Solution for Q 1 (In Graph. As. Matrix class) public Edge min. Weight. Edge(){ boolean is. First. Edge = true; Edge min = null; for(int i = 0; i < number. Of. Vertices; i++){ for(int j = 0; j < number. Of. Vertices; j++){ if(edges[i][j]!=null){ if(edges[i][j]. get. Weight()==null) throw new Illegal. Argument. Exception( "The graph is not weighted"); if(is. First. Edge){ min = edges[i][j]; is. First. Edge = false; } else if(edges[i][j]. get. Weight(). compare. To( min. get. Weight())<0) min = edges[i][j]; } } } return min; }