Implementation of Gaussian Beam Sources in FDTD for

Implementation of Gaussian Beam Sources in FDTD for Scattering Problems Lai-Ching Ma & Raj Mittra Electromagnetic Communication Laboratory The Pennsylvania State University Park, PA 16802 Emails: lcma@ieee. org, rajmittra@ieee. org

Outline l Motivation l Implementation and characteristics of the new Gaussian beam source l Parametric study of the new source implementation l Numerical examples l Conclusions

Motivation l To implement a focused source distribution, namely a Gaussian beam, for scattering problems in FDTD. – To eliminate the edge effects – To investigate the local behavior of the scattering phenomenon Some applications include scattering by: rough surfaces; photonic crystals. l TF/SF Interface PML k PML SF PML TF PML

Commonly used FDTD sources in scattering problems l Total-field/Scattered Field Formulation l Scattered Field Formulation SF SF TF TF/SF interface Incident fields are needed on the TF/SF interface only. l The scatterers must be totally enclosed by the TF/SF interface. l Incident fields are needed over the entire volume of the scatterer. l Computation of incident fields is difficult when the scatterer is comprised of frequency dependent materials. l

Implementation of Gaussian beam sources Based on the TF/SF formulation for plane wave ÞThe TF/SF interface is implemented on the illuminating surface, rather than on a closed box. Einc = Einco * exp( - 2/w 2 ) Einco = plane wave amplitude, w = beam width, = distance from the beam axis Beam width w ÞTo mimic a Gaussian beam, a Gaussian window is applied to a plane wave. progression on the TF/SF interface for plane wave ) PML SF TF/SF interface TF k (Direction defined by phase PML scatterer PML Incident field amplitude on TF/SF interface All six faces of computational domain are terminated by PMLs

Characteristics of the new source ØNo need to model or design a real antenna element that generates the desired source distribution. w ØEasy to implement. TF/SF Interface ØThe field distribution at the source location is the same as that of the desired source distribution ( unlike soft source ) while the source is transparent to the reflected fields from the scatterers (unlike hard source), provided that certain conditions are satisfied. PML k PML SF PML TF PML ØIn contrast to the situation when a closed TF/SF interface is used, the scatterer can now be allowed to touch the ABC to reduce the edge effect, and/or to model an infinitely large structure. ØTransmission and reflection characteristics can now be extracted easily.

Parametric study for the implementation of Gaussian beam sources Ø The modified method truncates the TF/SF by ABC Ø Test 1: Does any reflections come back from the absorbing boundary on the sides of interface ? Ø We have assumed that certain incident field distributions can be sustained to propagate in free space. Ø Test 2: Is such incident field distribution valid/physical for all frequencies ? Fix the physical beam width Test 1: Vary the TF/SF interface area Test 2: Vary the frequency => electric size of beam width Frequency Observation: How close is the field distribution at the TF/SF interface to the incident field distribution ?

Test 1: Varying the TF/SF interface area Case 1 edge: -9 d. B Case 2 edge: Normal incidence, Ex-pol. TF/SF interface (Lx. L) Beam width w = 90 mm Case 1: L = 2 w = 180 mm Frequency = 10 GHz Case 2: L = 3 w = 270 mm Beam width is 3 at 10 GHz Case 3: L = 4 w = 360 mm Case 1: L = 2 w Case 2: L = 3 w -20 d. B Case 3 edge: -35 d. B Case 3: L = 4 w Incident direction L Case 1 L FDTD Computed |Ex| at the TF/SF interface at 10 GHz Incident |Ex| set at the TF/SF interface No distortions for all cases.

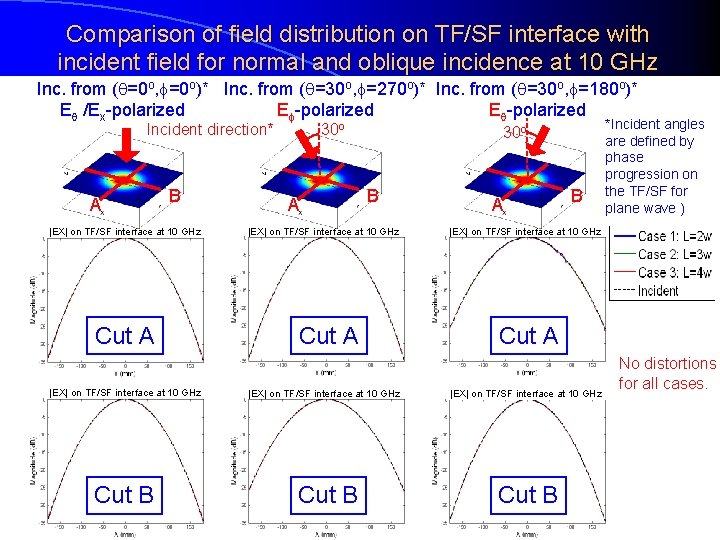
Comparison of field distribution on TF/SF interface with incident field for normal and oblique incidence at 10 GHz Inc. from ( =0 o, =0 o)* Inc. from ( =30 o, =270 o)* Inc. from ( =30 o, =180 o)* E /Ex-polarized E -polarized 30 o Incident direction* A B |EX| on TF/SF interface at 10 GHz Cut A |EX| on TF/SF interface at 10 GHz Cut B A 30 o B |EX| on TF/SF interface at 10 GHz Cut A |EX| on TF/SF interface at 10 GHz Cut B A B *Incident angles are defined by phase progression on the TF/SF for plane wave ) |EX| on TF/SF interface at 10 GHz Cut A |EX| on TF/SF interface at 10 GHz Cut B No distortions for all cases.

Test 2: Varying the frequency / Frequency/Electric size of beam width electric size of beam width f = 1. 67 GHz, w = 0. 5 f = 3. 33 GHz, w = 1. 0 f = 5. 0 GHz, w = 1. 5 f = 10. 0 GHz, w = 3 Normal incidence, Ex-pol. Beam width w = 90 mm TF/SF size L = 3 w = 270 mm Incident |Ex| set at the TF/SF interface (same at all freq. ) FDTD Computed |Ex| at the TF/SF interface f = 1. 67 GHz, w = 0. 5 Distortion f = 5. 0 GHz, w = 1. 5 Incident direction L L = 3 w f = 3. 33 GHz, w = 1. 0 f = 10. 0 GHz, w = 3. 0

Comparison of field distribution on TF/SF interface with incident field for normal and oblique incidence Inc. from ( =0 o, =0 o)* Inc. from ( =30 o, =270 o)* Inc. from ( =30 o, =180 o)* E /Ex-polarized E -polarized 30 o Incident direction* B A Cut A 30 o B A Cut A A B *Incident angles are defined by phase progression on the TF/SF for plane wave Cut A - Distortions for w = 0. 5 in all cases. Cut B - Slight distortion for w = 1. 0 at oblique incidence (E -polarized)

Example 1: Scattering by a homogeneous dielectric slab at oblique incidence Incident waves comes from ( =150 o, =0 o)*, E -polarized Gaussian beam width = 11 mm = 0. 55 at 15 GHz PML SF PML TF/SF Interface k Vertical field distribution |EY| at 15 GHz Transmitted beam TF Dielectric slab r=4 L=W=80 mm, D=19 mm (D=1. 9 at 15 GHz in dielectric) *Incident angles are defined by the phase progression on the TF/SF for plane wave PML TF Free space TF/SF interface Free space PML Slab SF SF Reflected beam Incident direction The incident beam is not seen in the figure because it is in the scattered field region.

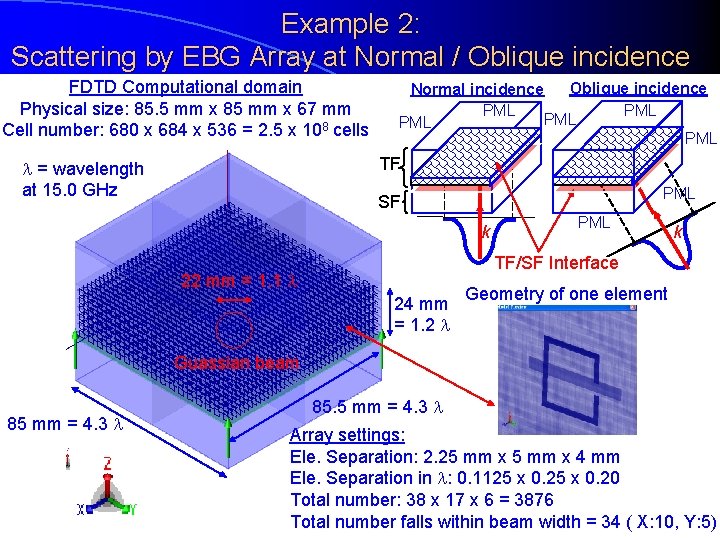
Example 2: Scattering by EBG Array at Normal / Oblique incidence FDTD Computational domain Physical size: 85. 5 mm x 85 mm x 67 mm Cell number: 680 x 684 x 536 = 2. 5 x 108 cells Oblique incidence Normal incidence PML PML PML TF = wavelength at 15. 0 GHz PML SF k PML k TF/SF Interface 22 mm = 1. 1 24 mm = 1. 2 Geometry of one element Guassian beam 85 mm = 4. 3 85. 5 mm = 4. 3 Array settings: Ele. Separation: 2. 25 mm x 4 mm Ele. Separation in : 0. 1125 x 0. 20 Total number: 38 x 17 x 6 = 3876 Total number falls within beam width = 34 ( X: 10, Y: 5)

Comparisons of Transmission/Reflection Coefficients with infinite array Periodic boundary conditions(PBC)/Plane wave VS Finite Array/Gaussian Beam for Normal Incidence PML PML TF PML SF k TF/SF interface k E = (0, Ey, 0) H = (Hx, 0, 0) Normal incidence In finite-array/gaussian-beam case, the transmission/reflection coefficients are computed from the fields on the Huygen’s surfaces in the total field and scattered field region, respectively, followed by normalization using the incident power propagating in forward direction.

Comparisons of Transmission/Reflection Coefficients with infinite array Periodic boundary conditions(PBC)/Plane wave VS Finite Array/Gaussian Beam for TE and TM Oblique Incidence (30 o) TMz =30 o E = (0, Ey, Ez) H = (Hx, 0, 0) k TEz PML TF SF =30 o E = (0, Ey, 0) H = (Hx, 0, Hz) PML PML k k

Normal Incidence -- Field Distribution at 15. 0 GHz P 4 P 3 P 2 P 1 TF/SF interface just below the array P 3 P 1: XY Plane Incident direction Transmission/Reflection P 3: XZ Plane (just above the array) P 4 Array: 6 layers P 2: XY Plane (~1 from array) P 4: YZ Plane

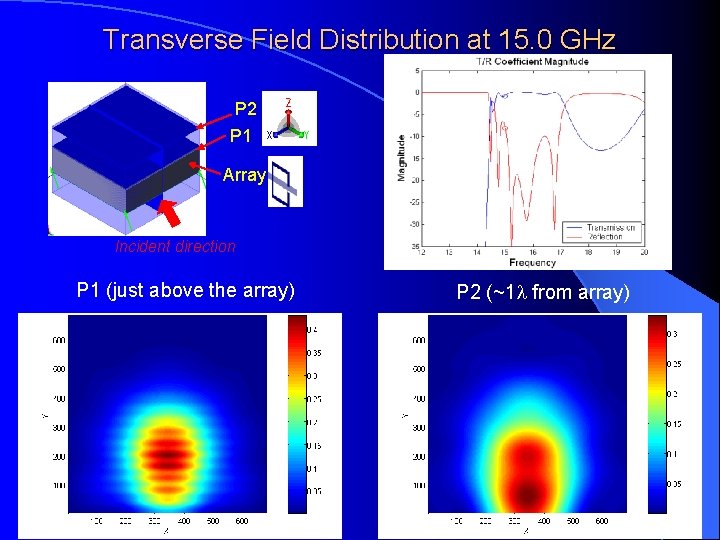
Transverse Field Distribution at 15. 0 GHz P 2 P 1 Array Incident direction P 1 (just above the array) P 2 (~1 from array)

P 2 P 1 Vertical Field Distribution at 15. 0 GHz Array P 4: YZ Plane Dielectric Slab Free space Incident direction EBG Array Incident direction P 4: YZ Plane in Transmission region Free space Dielectric Slab EBG Array

Conclusions Ø An implementation of Gaussian beam sources based on the TF/SF formulation in FDTD has been introduced. It can be used for various scattering problems that require tapered illumination, as opposed to a plane wave incident field. w TF/SFInterface PML TF/SF k PML SF TF PML Ø The present method not only preserves the desirable features of the TF/SF formulation, but also allows the scatterers to touch the absorbing boundary to reduce the edge effect. This feature enables us to model an infinitely large structure, which is not possible in the conventional TF/SF approach. Ø The criteria for accurately constructing the Gaussian beam distribution can be on the TF/SF interface have been determined. They are: Ø The incident field must decay to a low level at the four edges of TF/SF interface. Ø The dimension of the Gaussian beam width should be larger than one wavelength. Ø Two numerical examples have been presented to demonstrate the application of this new source to practical scattering problems.