Implementation of digital filters in FPGA for Tile

Implementation of digital filters in FPGA for Tile energy reconstruction per bunch crossing Pablo Moreno - IFIC/UV Luciano Manhâes - UFJF

Introduction

Background • The digitized signal of the PMTs provides information of energy and timing for each Tile. Cal channel • In order to obtain these to magnitudes, this signal has to be processed: Energy and time reconstruction • In the present system, this processing is performed using DSPs and sequential algorithms for the online reconstruction • The purpose of this work is to study the implementation of digital filters for online energy reconstruction per bunch crossing using FPGAs 3

The problem • The PMT impulse response has certain shape • Some PMT pulses may overlap • The correlation between PMT input and output is 0. 79 4

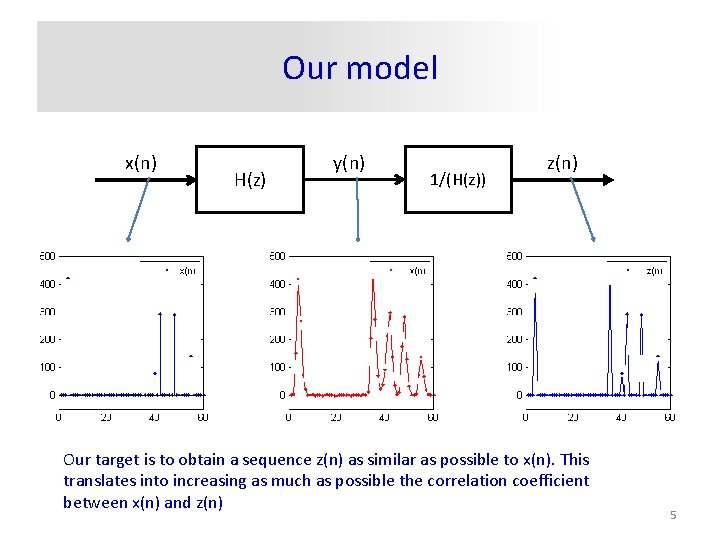
Our model x(n) H(z) y(n) 1/(H(z)) z(n) Our target is to obtain a sequence z(n) as similar as possible to x(n). This translates into increasing as much as possible the correlation coefficient between x(n) and z(n) 5

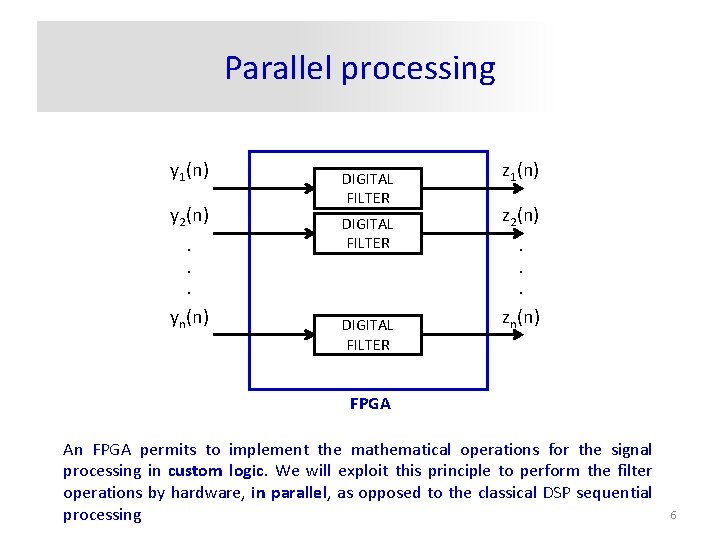
Parallel processing y 1(n) y 2(n). . . yn(n) DIGITAL FILTER z 1(n) z 2(n). . . zn(n) FPGA An FPGA permits to implement the mathematical operations for the signal processing in custom logic. We will exploit this principle to perform the filter operations by hardware, in parallel, as opposed to the classical DSP sequential processing 6

Implementation

FIR filters in FPGA • There are two types of digital filters according to their impulse response: FIR and IIR • The design of a stable IIR filter* for Tile. Cal energy is more complicated and needs to be studied deeper • For simplicity, we will focus the work on the implementation of FIR filters in some of their most common structures • We want to evaluate its implementation in terms of FPGA resources and speed • Main target is to figure out whether 48 channels can be reconstructed within a single FPGA – One of the purposes of the SROD demonstrator for phase 0 • (*) See: https: //indico. cern. ch/get. File. py/access? contrib. Id=0&res. Id=0&material. Id=slides&c onf. Id=213577 8

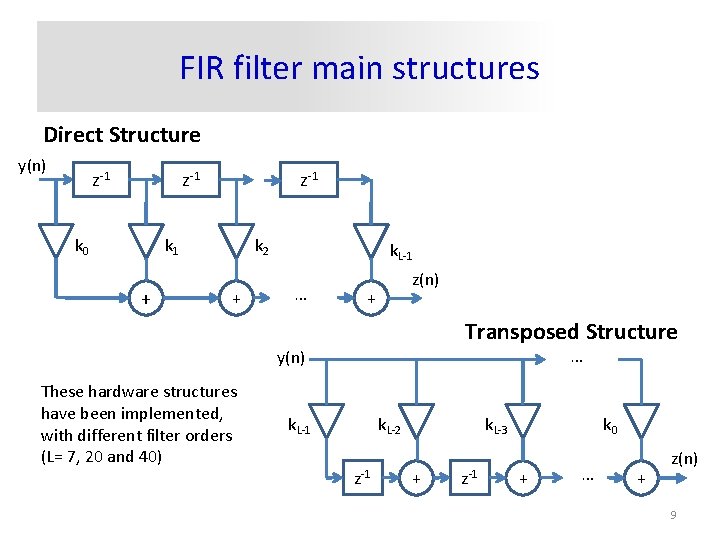
FIR filter main structures Direct Structure y(n) z-1 k 0 z-1 k 1 + k 2 + k. L-1 … z(n) + Transposed Structure … y(n) These hardware structures have been implemented, with different filter orders (L= 7, 20 and 40) k. L-1 k. L-2 z-1 k. L-3 + z-1 k 0 + … + z(n) 9

DSP Slice in a Virtex 7 A V 7 device contains 2800 DSP slices… 10

Synthesis details • The filter has been described in VHDL • Generic parameters allow to customize the filter (L, data word length, coefficient word length…) • Access to DSP block is derived by the synthesis tools when a multiplication is found on the code 11

Coefficient loading • It is desired that coefficient values can be updated at beginning of a run • There is an input for the coefficients on the design: they can be loaded • A control signal disables data processing during the load of the coefficients • Each coefficient is stored in a dedicated register (tap of the filter) • Coefficients are loaded shifting the contents of the registers until they reach their final position z-1 clk cycle = 1 z-1 k. L-1 + z-1 … + z-1 + clk cycle =-12 z k. L-1 k. L-2 + z-1 z k 0 +. . . -1 clk cycle =-1 L z k 1 + … + k 2 + k. L-1 … + 12

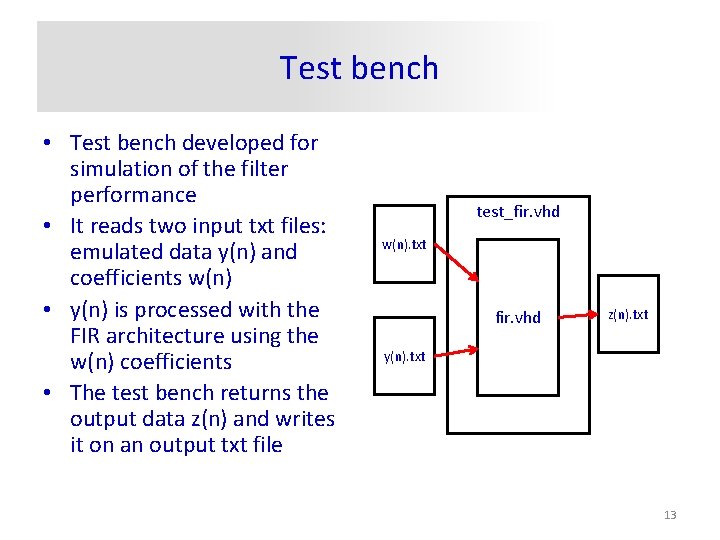
Test bench • Test bench developed for simulation of the filter performance • It reads two input txt files: emulated data y(n) and coefficients w(n) • y(n) is processed with the FIR architecture using the w(n) coefficients • The test bench returns the output data z(n) and writes it on an output txt file test_fir. vhd w(n). txt fir. vhd z(n). txt y(n). txt 13

Results

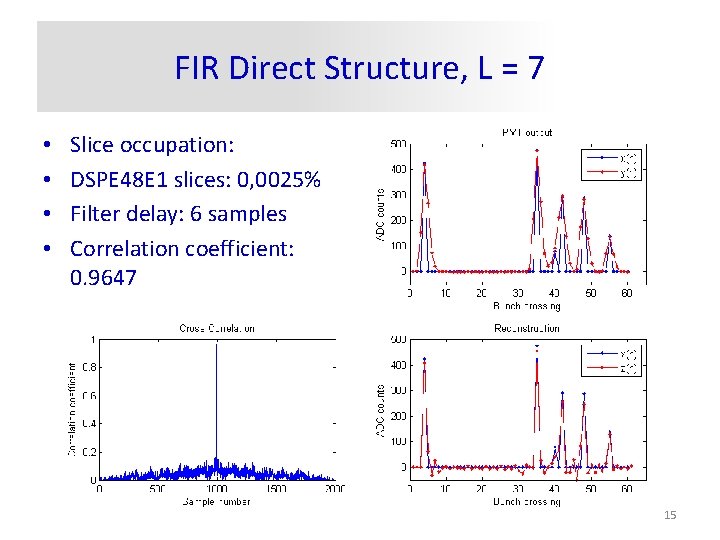
FIR Direct Structure, L = 7 • • Slice occupation: DSPE 48 E 1 slices: 0, 0025% Filter delay: 6 samples Correlation coefficient: 0. 9647 15

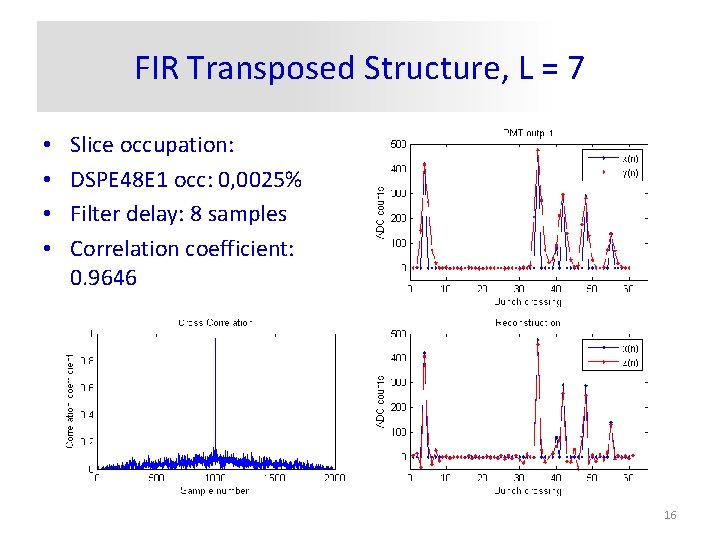
FIR Transposed Structure, L = 7 • • Slice occupation: DSPE 48 E 1 occ: 0, 0025% Filter delay: 8 samples Correlation coefficient: 0. 9646 16

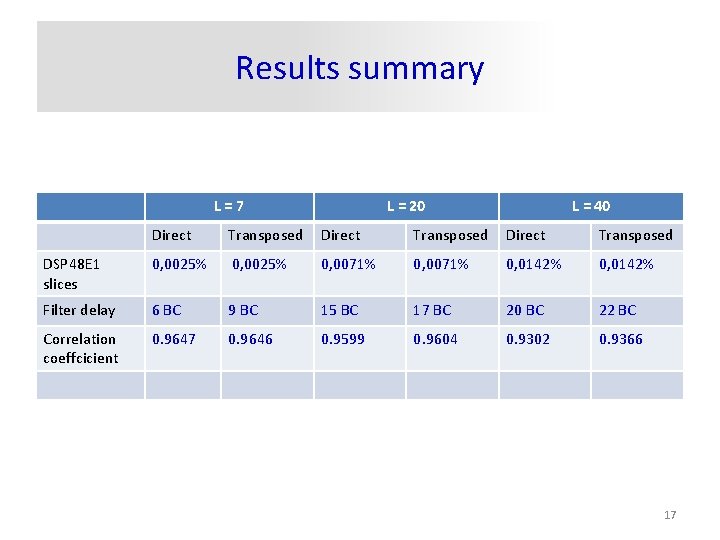
Results summary L=7 L = 20 L = 40 Direct Transposed DSP 48 E 1 slices 0, 0025% 0, 0071% 0, 0142% Filter delay 6 BC 9 BC 15 BC 17 BC 20 BC 22 BC Correlation coeffcicient 0. 9647 0. 9646 0. 9599 0. 9604 0. 9302 0. 9366 17

48 channels implementation • Direct Structure – Occupied FPGA logic: 5. 68% – Occupied DSP 48 E 1: 34. 29% – Fmax: 649 MHz • Transposed structure – Occupied FPGA logic: 0. 07% – Occupied DSP 48 E 1: 34. 29% – Fmax: 361 MHz 18

Summary and next steps • Direct and Transposed FIR structures implemented on a V 7 FPGA • Results for individual channels show the performance of the filter • Seems that 7 coefficients is the best option – Coefficients quantization effects to be studied further • Architecture effects (i. e. speed differences) to be understood and studied further 19

References • Digital Signal Processing with Field Programmable Gate Arrays, U. Meyer-Baese, Springer • Digital Signal Processing – A computer-Based Approach, Sanjit K. Mitra 20