Implementation of a noise subtraction algorithm using Verilog

Implementation of a noise subtraction algorithm using Verilog HDL University of Massachusetts, Amherst Department of Electrical & Computer Engineering, Course 559/659 by Perry Levy, Aseem Pangotra, Stephan Stiglmayr and Thomas Kunkel Team Leader: Prof. Maciej Ciesielski

Noise-subtracting algorithm " Time to frequency transformation " Subtraction of magnitudes " Distortion correction " Frequency to time transformation Algorithm Modules In- / Output FFT Subtraction

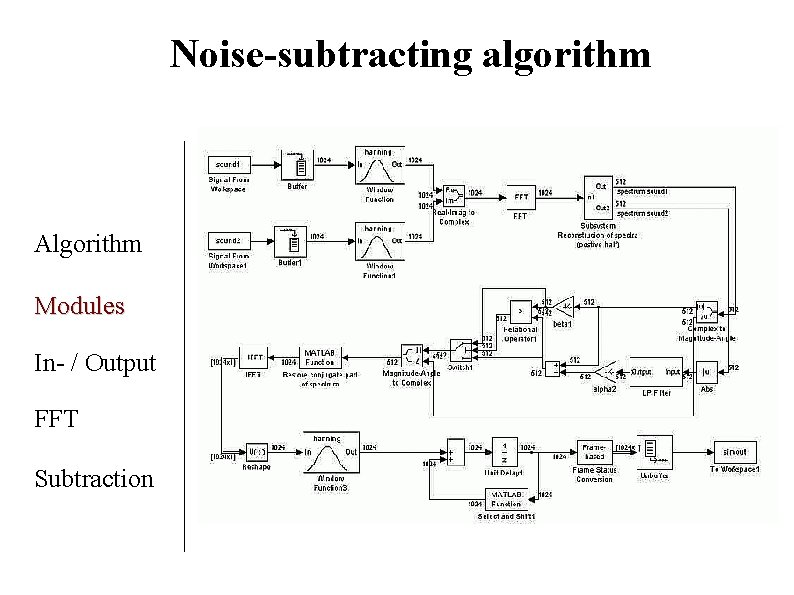
Noise-subtracting algorithm Algorithm Modules In- / Output FFT Subtraction

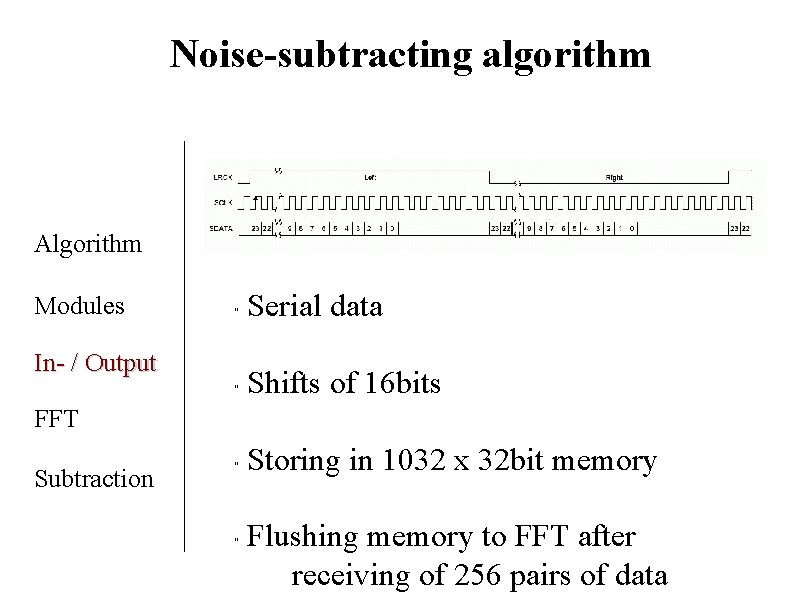
Noise-subtracting algorithm Algorithm Modules " Serial data " Shifts of 16 bits " Storing in 1032 x 32 bit memory In- / Output FFT Subtraction " Flushing memory to FFT after receiving of 256 pairs of data

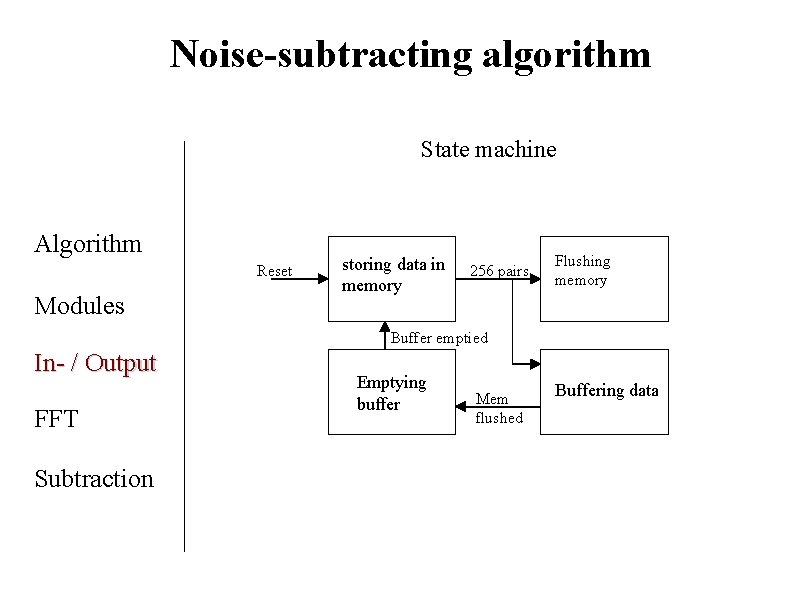
Noise-subtracting algorithm State machine Algorithm Reset Modules storing data in memory 256 pairs Flushing memory Buffer emptied In- / Output FFT Subtraction Emptying buffer Mem flushed Buffering data

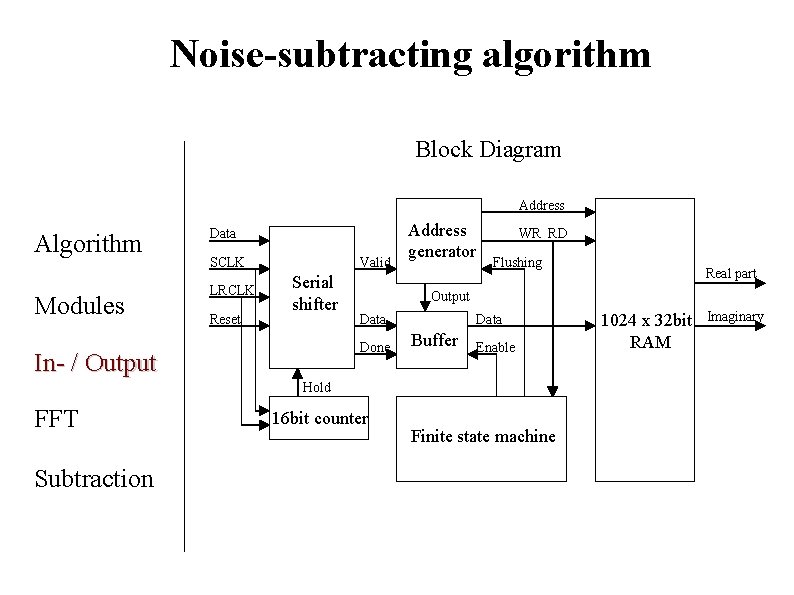
Noise-subtracting algorithm Block Diagram Address Algorithm Modules Data SCLK LRCLK Reset Valid Serial shifter WR RD Flushing Data Buffer Enable Hold FFT Subtraction Real part Output Done In- / Output Address generator 16 bit counter Finite state machine 1024 x 32 bit RAM Imaginary

Noise-subtracting algorithm " Algorithm " Modules In- / Output " FFT Subtraction Parallel input and output of variables 16 Bit address, 8 Bit data (compatible to microcontroller) Preset values when resetting

Noise-subtracting algorithm " Implementation of Radix 2 algorithm " Window length 1024 " 16 Bit fixed point arithmetics Algorithm Modules In- / Output FFT " Subtraction " 2 FFTs at the same time by using real and imaginary signal Reconstruction afterwards needed

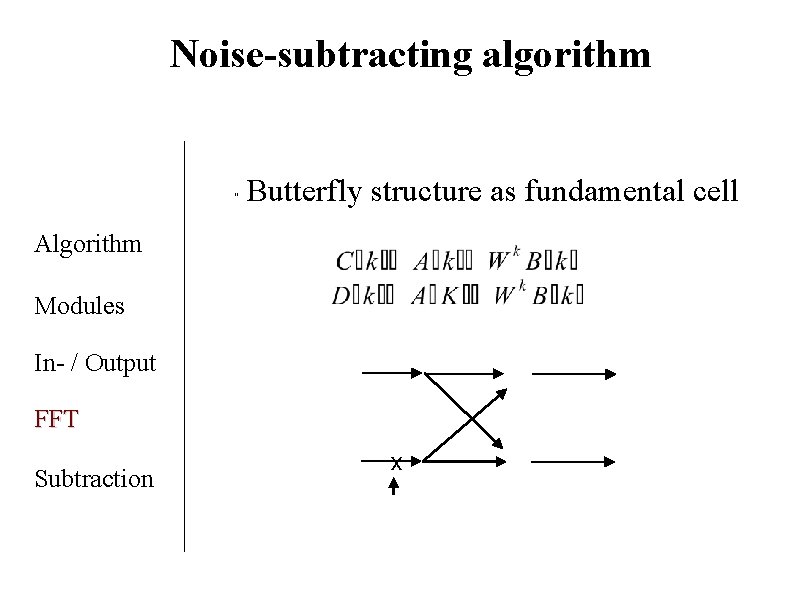
Noise-subtracting algorithm " Butterfly structure as fundamental cell Algorithm Modules In- / Output FFT Subtraction x

Noise-subtracting algorithm Signal-flow Graph for 8 point FFT f(0) Algorithm F(0) F(1) -1 W 0 Modules -1 In- / Output W 2 -1 F(2) -1 F(3) W 0 FFT W 1 -1 W 0 Subtraction f(7) -1 W 2 W 3 -1 -1 -1 F(4) F(5) -1 F(6) -1 F(7)

Noise-subtracting algorithm " Algorithm " Modules In- / Output Sequential implementation 1 Bit shiftdown after each step to prevent overflow " RAM 1024 x 32 Bit " Controller (Finite state machine) " Address generator FFT Subtraction

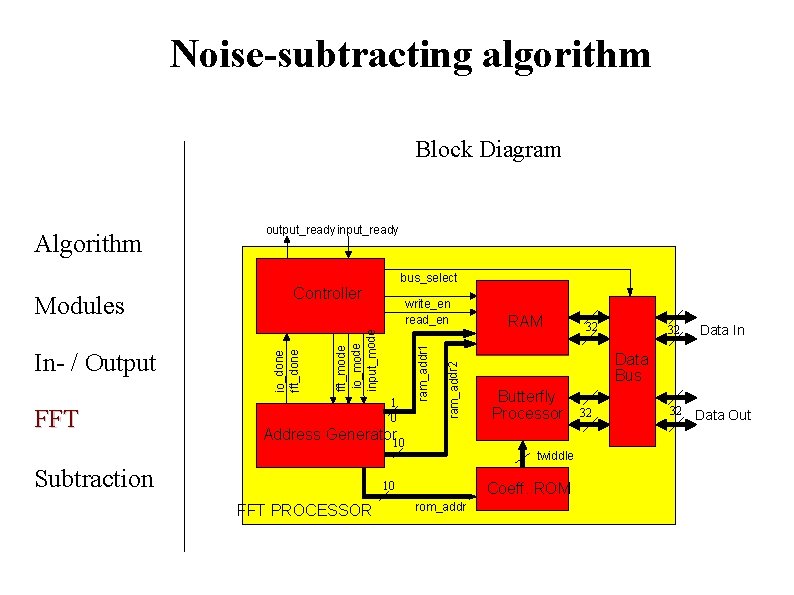
Noise-subtracting algorithm Block Diagram Algorithm output_ready input_ready bus_select ram_addr 1 1 0 ram_addr 2 FFT write_en read_en fft_mode io_mode input_mode In- / Output io_done fft_done Modules Controller Address Generator 10 Subtraction Butterfly Processor Coeff. ROM rom_addr 32 32 Data In 32 Data Out Data Bus twiddle 10 FFT PROCESSOR RAM 32

Noise-subtracting algorithm Delay estimation Algorithm • Input: Modules • FFT processing: • output: In- / Output FFT Subtraction Sum 512 2*512*10 512 11264 clock cycles

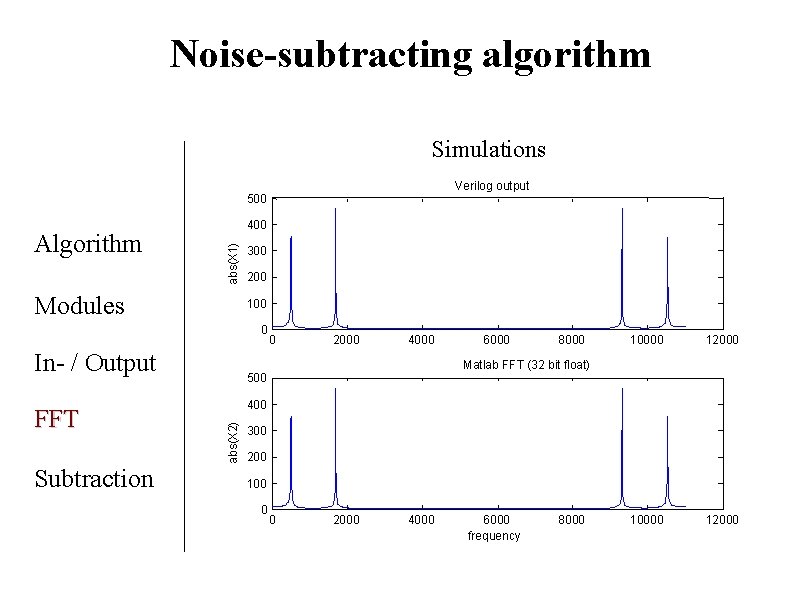
Noise-subtracting algorithm Simulations Verilog output 500 abs(X 1) Algorithm 400 Modules 300 200 100 0 In- / Output Subtraction 2000 4000 6000 8000 10000 12000 Matlab FFT (32 bit float) 500 400 abs(X 2) FFT 0 300 200 100 0 0 2000 4000 6000 frequency 8000

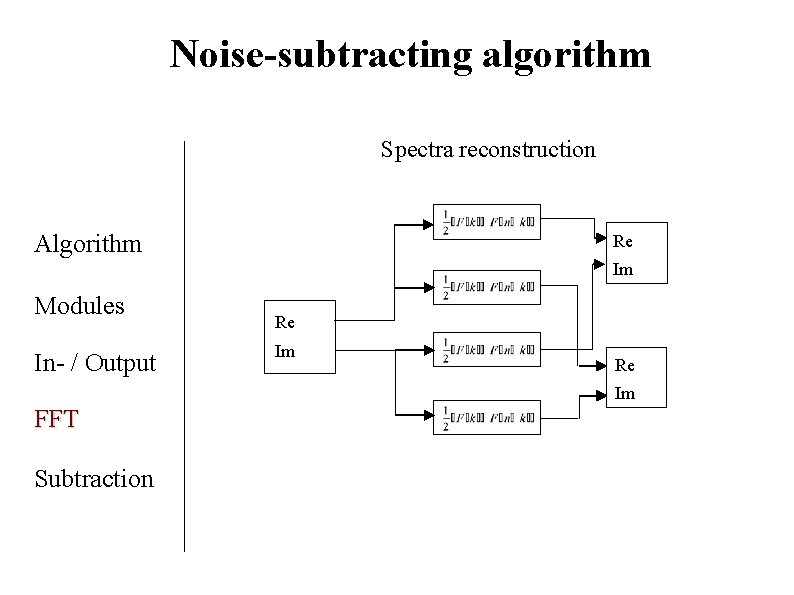
Noise-subtracting algorithm Spectra reconstruction Algorithm Re Im Modules In- / Output Re Im FFT Subtraction

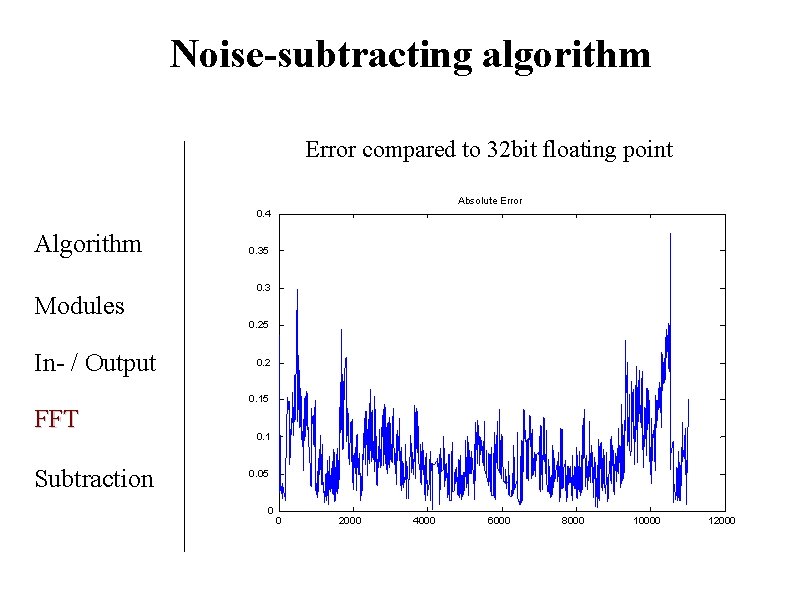
Noise-subtracting algorithm Error compared to 32 bit floating point Absolute Error 0. 4 Algorithm Modules In- / Output FFT Subtraction 0. 35 0. 3 0. 25 0. 2 0. 15 0. 1 0. 05 0 0 2000 4000 6000 8000 10000 12000

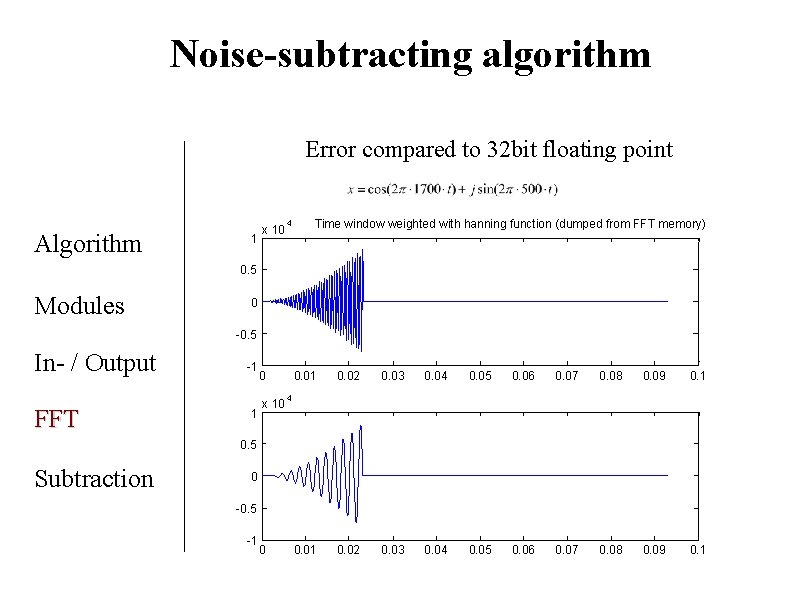
Noise-subtracting algorithm Error compared to 32 bit floating point Algorithm 1 x 10 4 Time window weighted with hanning function (dumped from FFT memory) 0. 5 Modules 0 -0. 5 In- / Output FFT -1 1 0 x 10 0. 01 0. 02 0. 03 0. 04 0. 05 0. 06 0. 07 0. 08 0. 09 0. 1 4 0. 5 Subtraction 0 -0. 5 -1 0

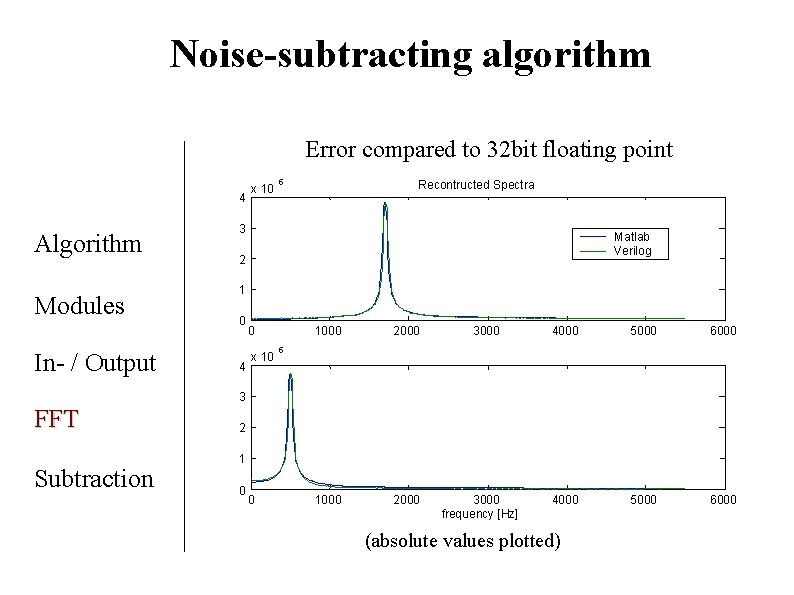
Noise-subtracting algorithm Error compared to 32 bit floating point 4 Algorithm Modules In- / Output x 10 5 Recontructed Spectra 3 Matlab Verilog 2 1 0 4 0 x 10 1000 2000 3000 4000 5000 6000 5 3 FFT Subtraction 2 1 0 0 3000 frequency [Hz] (absolute values plotted)

C. O. R. D. I. C • An acroynm for: – Coordinate Rotation DIgital Computer

CORDIC? WHY USE IT? " " CORDIC was derived by Volder in the 50’s to calculate trigonometric function. CORDIC can also calculate hyperbolic, linear and logarithmic functions. CORDIC processing offers high computational rates fast enough for demanding DSP tasks. Hardware-efficient algorithm, requires only shifts and adds.

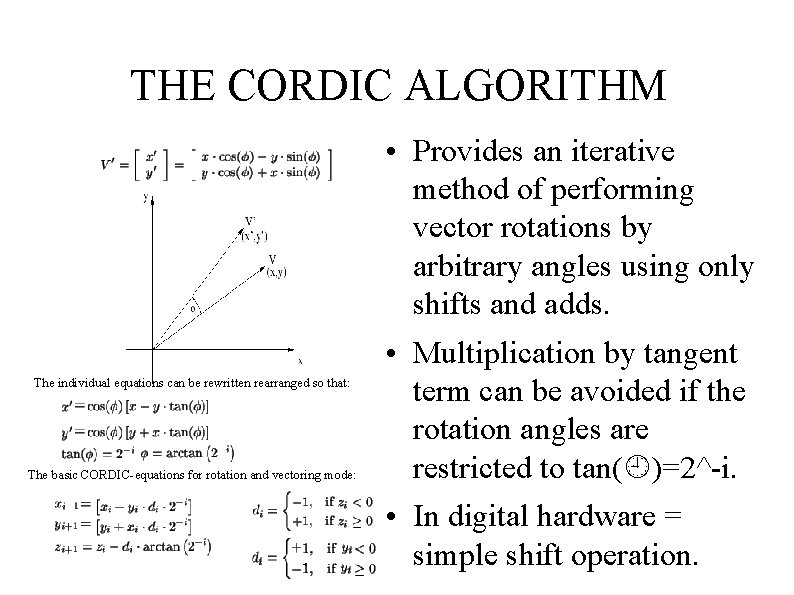
THE CORDIC ALGORITHM The individual equations can be rewritten rearranged so that: The basic CORDIC-equations for rotation and vectoring mode: • Provides an iterative method of performing vector rotations by arbitrary angles using only shifts and adds. • Multiplication by tangent term can be avoided if the rotation angles are restricted to tan( )=2^-i. • In digital hardware = simple shift operation.

Vectoring and Rotation Modes • Vectoring mode performs Cartesian to Polar transformation by rotating input vector to the x-axis while recording the angle required to make that rotation. • Rotation mode performs Polar to Cartesian transformation by rotating the input vector by a specified angle (given as an argument).

Word-Parallel Pipelined CORDIC • CORDIC Processor core built around three fundamental modules: – Pre-Processor: manipulates inputs to fit in -1 to +1 rad. so that the algorithm covers entire 2 range. – CORDIC core: performs actual algorithm in parallel using a pipeline of Cordic. Pipe blocks. – Post-Processor: places results in correct quadrant.

RECTANGULAR TO POLAR CONVERSION • Takes two 16 -bit signed words as inputs (Xin, Yin) • CORDIC core returns equivalent polar coordinates where Rout is the magnitude and Aout is the angle. • Outputs are in fractional format with the upper 16 -bits represent decimal value and lower 4 -bits represent fractional value.

POLAR TO RECTANGULAR CONVERSION • Takes 16 -bit magnitude from subtraction and stored angle as inputs (Rin, Ain). • CORDIC core returns equivalent rectangular coordinates Xo and Yo. • Core only converges in the range -90 to +90 degrees, must write a pre and post processor so that algorithm covers entire 2 range.

FUTURE WORK " " Need to write test bench for rect 2 polar and polar 2 rect modules. Need to finish writing pre and post processor for polar 2 rect module. Need to connect my modules to my partners modules. Need to test and verify that they work well together.

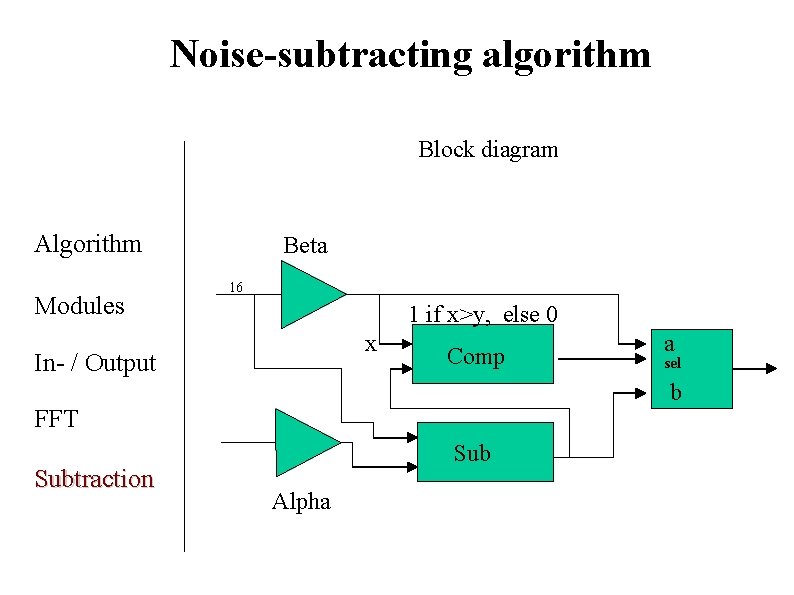
Noise-subtracting algorithm Block diagram Algorithm Modules Beta 16 1 if x>y, else 0 x In- / Output Comp sel b FFT Subtraction a Sub Alpha

Noise-subtracting algorithm • Algorithm ( A and B) • Modules • In- / Output • FFT Subtraction Inputs: two, 16 unsigned bits each • Multiplication: Alpha and Beta terms Subtraction: ((original A)-(Alpha*B)) Comparators: (A > B) out =1, else out =0 Multiplexer: (Inputs: Select, A*Beta, subtractor output) Select = 1, final_out = x Select = 0, final_out = y

FUTURE WORK " Connect all modules together. " Need to write and verify RTL code. " Synthesize all code and implement in FPGA. " Test FPGA.