IMDD vs Coherent Will Datacenter be the New

IMDD vs Coherent Will Datacenter be the New Battleground? Summer Topicals 2020 Virtual Conference Tutorial Tu. A 2. 2 10: 45 AM – 11: 30 AM MDT 14 July 2020 Chris Cole

Outline • NRZ vs HOM • • • Serial vs WDM Coherent in Telecom Coherent in Datacom IMDD vs Coherent SNR Intra Datacenter Optics Appendices IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 2 14 July 2020 Chris Cole Luminous Computing

Shannon-Hartley Theorem C = B log 2 (1 + S/N) C ≜ Channel capacity B ≜ Bandwidth S ≜ Signal Power N ≜ Noise Power Guidance to increase C: If B limited, use S/N to increase modulation order If S/N limited, use B to increase Baud rate C. Cole, “SMF PMD Modulation Observations”, 400 Gb/s Ethernet Task Force, IEEE 802. 3 Plenary Session, Berlin, Germany, 10 -12 March 2015 cc IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 3 14 July 2020 Chris Cole Luminous Computing
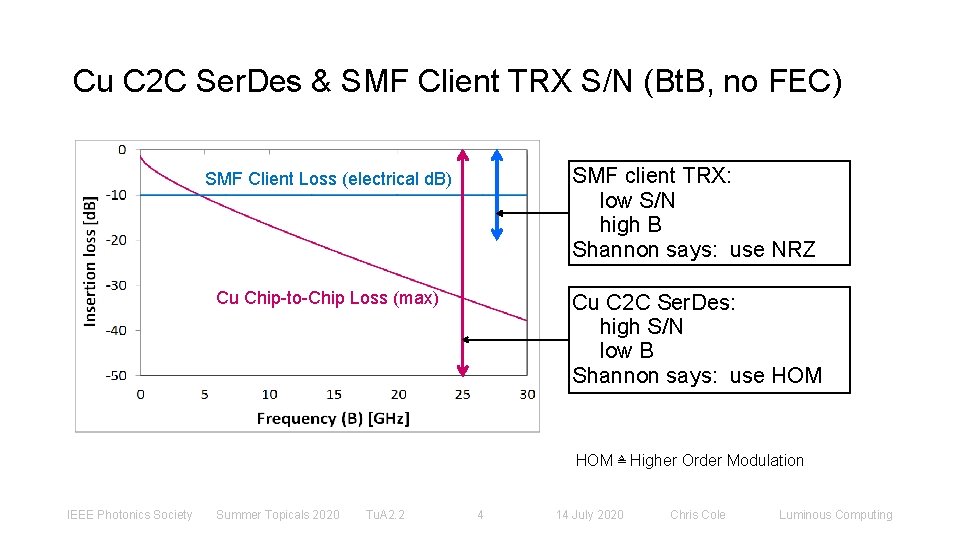
Cu C 2 C Ser. Des & SMF Client TRX S/N (Bt. B, no FEC) SMF Client Loss (electrical d. B) SMF client TRX: low S/N high B Shannon says: use NRZ Cu Chip-to-Chip Loss (max) Cu C 2 C Ser. Des: high S/N low B Shannon says: use HOM ≜ Higher Order Modulation IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 4 14 July 2020 Chris Cole Luminous Computing
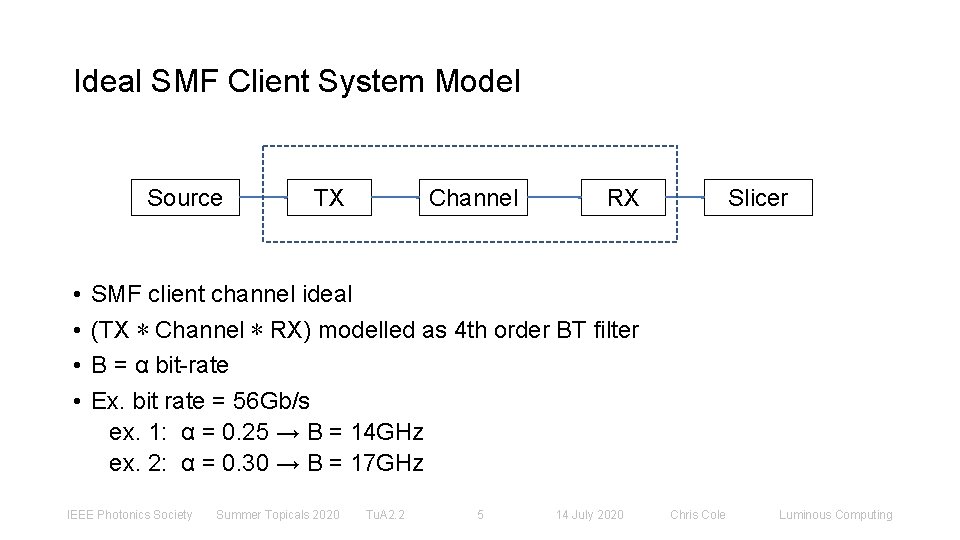
Ideal SMF Client System Model Source • • TX Channel RX Slicer SMF client channel ideal (TX ∗ Channel ∗ RX) modelled as 4 th order BT filter B = α bit-rate Ex. bit rate = 56 Gb/s ex. 1: α = 0. 25 → B = 14 GHz ex. 2: α = 0. 30 → B = 17 GHz IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 5 14 July 2020 Chris Cole Luminous Computing
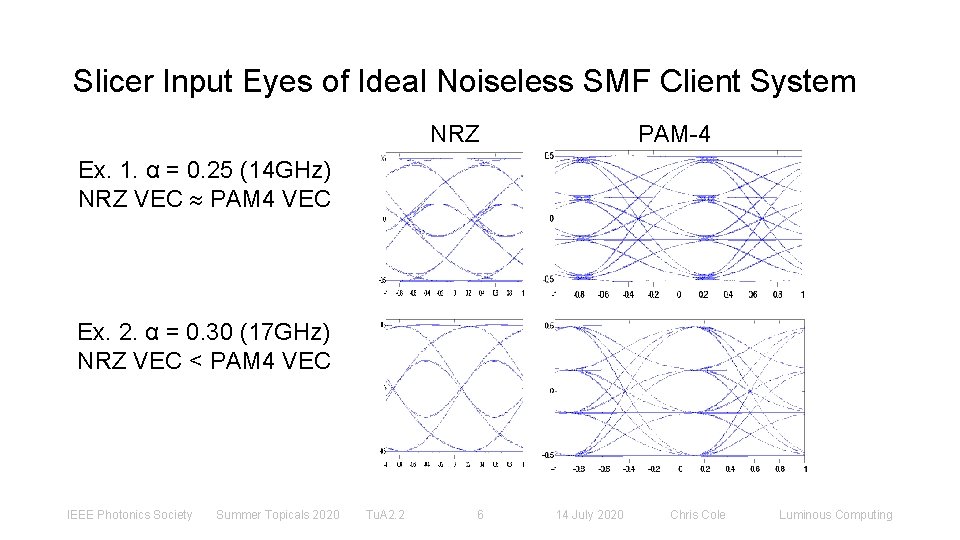
Slicer Input Eyes of Ideal Noiseless SMF Client System NRZ PAM-4 Ex. 1. α = 0. 25 (14 GHz) NRZ VEC PAM 4 VEC Ex. 2. α = 0. 30 (17 GHz) NRZ VEC < PAM 4 VEC IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 6 14 July 2020 Chris Cole Luminous Computing
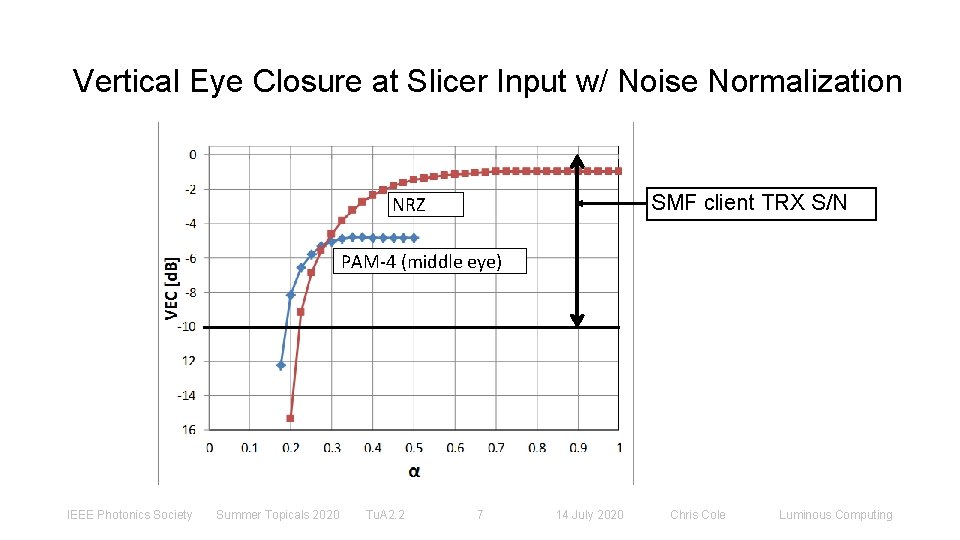
Vertical Eye Closure at Slicer Input w/ Noise Normalization SMF client TRX S/N NRZ PAM-4 (middle eye) IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 7 14 July 2020 Chris Cole Luminous Computing

IEEE Modulation Choice for 50 Gb/s and Faster Rates • Optics is the tail on the IC industry dog • 50 G PAM 4 ASIC Ser. Des was first developed for the Cu channel • IC Vendors wanted to maximize their ADC and DSP investment • IC dog wagged the optics tail • IEEE ignored Shannon • PAM 4 standardized for 50 G and 100 G Ethernet optical lane rates • 200 G (4 x 50 G PAM 4) FR 4 will soon ship in the millions • Optics & electronics today easily support 50 G NRZ • Extra cost and power of 50 G PAM 4 ADC, DSP, SNR locked-in forever IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 8 14 July 2020 Chris Cole Luminous Computing

Outline • NRZ vs HOM • Serial vs WDM • • • Coherent in Telecom Coherent in Datacom IMDD vs Coherent SNR Intra Datacenter Optics Appendices IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 9 14 July 2020 Chris Cole Luminous Computing

Ethernet Optics History: 1 & 10 Gb. E • 1 Gb. E standard adopted in 1998 • 1λ Serial NRZ (LX) • Shipped in the millions • 10 Gb. E standard adopted in 2002 • 4λ WDM NRZ (LX 4) • 1λ Serial NRZ (LR 4) • 5 -year delay in 10 Gb. E adoption after 90’s Tech bubble collapse • 10 GBaud optics & electronics matured to easily support 10 G NRZ • 10 G LR 4 shipped in the millions • 10 G LX 4 became a sad footnote in Ethernet optics history • “Serial is always cheaper” myth is born IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 10 14 July 2020 Chris Cole Luminous Computing

Ethernet Optics History: 40 Gb. E • 40 Gb. E standard adopted in 2010 • “Serial is always cheaper” myth well established • Fierce debate in the IEEE between: • 4λ WDM NRZ (LR 4) vs. • 1λ Serial NRZ (FR) • IEEE split the baby, adopted both • 40 G LR 4 shipped in the millions • 40 G FR became a sad footnote in Ethernet optics history IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 11 14 July 2020 Chris Cole Luminous Computing

Ethernet Optics History: 100 Gb. E • 100 Gb. E standard, targeted at the datacenter, adopted in 2015 • “Serial is always cheaper” myth going strong • Fierce debate in the IEEE about duplex SMF spec between: • 4λ CWDM NRZ (FR 4) • 1λ Serial PAM 16/8 (FR) • IEEE could not reach agreement, and neither was adopted • 100 G CWDM 4 spec developed immediately after in an MSA in 6 months • Shipped in the millions • 100 G PAM 16/8 became a sad footnote in Ethernet optics history • $240 M SNR math lesson for Cisco IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 12 14 July 2020 Chris Cole Luminous Computing

Ethernet Optics History: 400 Gb. E • 400 Gb. E standard adopted in 2017 • “Serial is always cheaper” myth unwavering • Fierce debate in the IEEE between: • 2λ*50 G WDM for 100 G FR 2 and 8λ*50 G LWDM 400 G LR 8 • 1λ*100 G Serial for 100 G FR and 400 G PSM DR 4 • IEEE split the baby, adopted 400 G LR 8 and DR 4, but no 100 G FR 2 • 400 G 8λ*50 G LWDM LR 8 shipped in low volume into early Telecom apps • 400 G 4λ*100 G CWDM FR 4 standardized soon afterwards IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 13 14 July 2020 Chris Cole Luminous Computing

Ethernet Optics History: 400 Gb. E (2) • Ethernet optics sad story 1: no Web 2. 0 deployment of 400 Gb. E • Huge industry R&D investment into 1 st Gen 400 Gb. E DR 4 & FR 4 with no ROI • 2 nd Gen 400 Gb. E will start shipping in volume in 2023 or later when Ethernet switches ship with 100 G I/O • Ethernet optics sad story 2: no low-cost, low-power 2λ 100 Gb. E optics matched to today’s Ethernet switches with 50 G I/O, forcing shipment of: • 4λ 100 G CWDM 4 with 1: 2 reverse gearbox (most Web 2. 0 s), or • 1λ 100 G FR with 2: 1 forward gearbox (Amazon mainly) • Either way, significant cost and power added to 100 G Ethernet optical links IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 14 14 July 2020 Chris Cole Luminous Computing

Outline • NRZ vs HOM • Serial vs WDM • Coherent in Telecom • • Coherent in Datacom IMDD vs Coherent SNR Intra Datacenter Optics Appendices IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 15 14 July 2020 Chris Cole Luminous Computing

G. 652 SMF DWDM Transport C-band Spec Limits • Loss • nom, max: 0. 2, 0. 28 d. B/km • IF link SNR was only determined by link loss • Coherent SNR 2 x IMDD SNR, in d. B • Coherent reach 2 x IMDD reach, i. e. half the amplifier cost • Bandwidth (B) • Spectral Efficiency is key metric because of fiber deployment cost • G. 694. 1 channel bandwidths: 25 to 100 GHz • Coherent has 4 orthogonal channels: I, Q, TE, TM • Shannon says: If B limited, use S/N to increase modulation order IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 16 14 July 2020 Chris Cole Luminous Computing
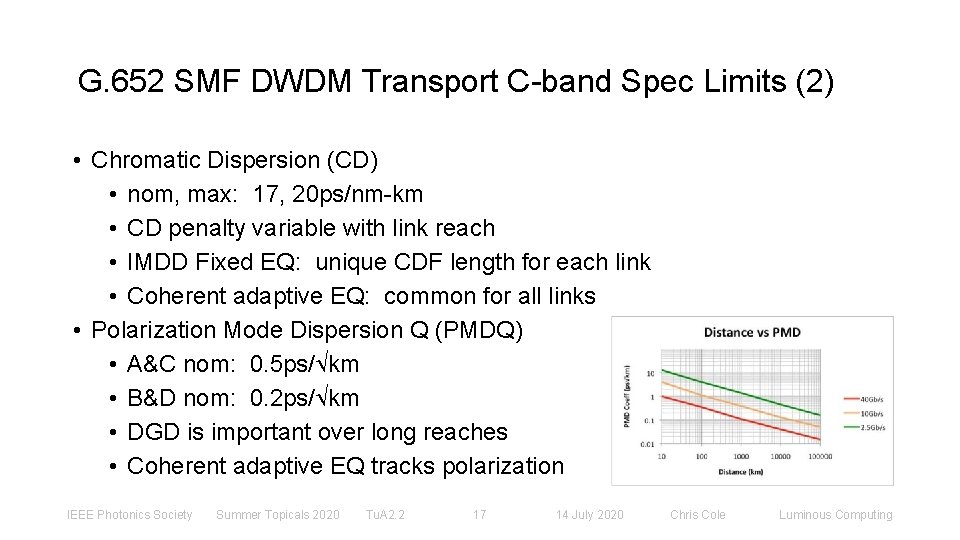
G. 652 SMF DWDM Transport C-band Spec Limits (2) • Chromatic Dispersion (CD) • nom, max: 17, 20 ps/nm-km • CD penalty variable with link reach • IMDD Fixed EQ: unique CDF length for each link • Coherent adaptive EQ: common for all links • Polarization Mode Dispersion Q (PMDQ) • A&C nom: 0. 5 ps/ km • B&D nom: 0. 2 ps/ km • DGD is important over long reaches • Coherent adaptive EQ tracks polarization IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 17 14 July 2020 Chris Cole Luminous Computing
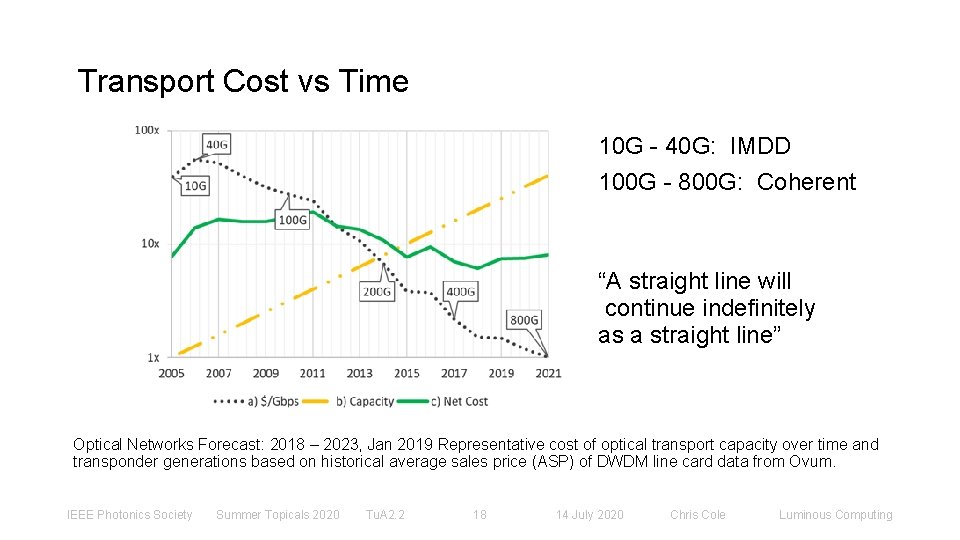
Transport Cost vs Time 10 G - 40 G: IMDD 100 G - 800 G: Coherent “A straight line will continue indefinitely as a straight line” Optical Networks Forecast: 2018 – 2023, Jan 2019 Representative cost of optical transport capacity over time and transponder generations based on historical average sales price (ASP) of DWDM line card data from Ovum. IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 18 14 July 2020 Chris Cole Luminous Computing

Outline • NRZ vs HOM • Serial vs WDM • Coherent in Telecom • Coherent in Datacom • IMDD vs Coherent SNR • Intra Datacenter Optics • Appendices IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 19 14 July 2020 Chris Cole Luminous Computing

G. 652 1 km SMF CWDM 4 O-band Spec Limits • Loss • max: 0. 47 d. B • Connectors and other passives determine link loss • Nom link loss budget: 4 d. B • SMF loss is not important • Bandwidth (B) • 4 wavelength band: 10 THz • 1 wavelength channel: 800 GHz • Shannon says: If S/N limited, use B to increase Baud rate • SMF bandwidth is not important IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 20 14 July 2020 Chris Cole Luminous Computing

G. 652 1 km SMF CWDM 4 O-band Spec Limits (2) • Chromatic Dispersion (CD) • min: -6 ps/nm • max: 3 ps/nm • SMF CD penalty is not important • Polarization Mode Dispersion Q (PDMQ) • A&C nom: 0. 5 ps • B&D nom: 0. 2 ps • SMF DGD penalty is not important IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 21 14 July 2020 Chris Cole Luminous Computing

Outline • • NRZ vs HOM Serial vs WDM Coherent in Telecom Coherent in Datacom • IMDD vs Coherent SNR • Intra Datacenter Optics • Appendices IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 22 14 July 2020 Chris Cole Luminous Computing
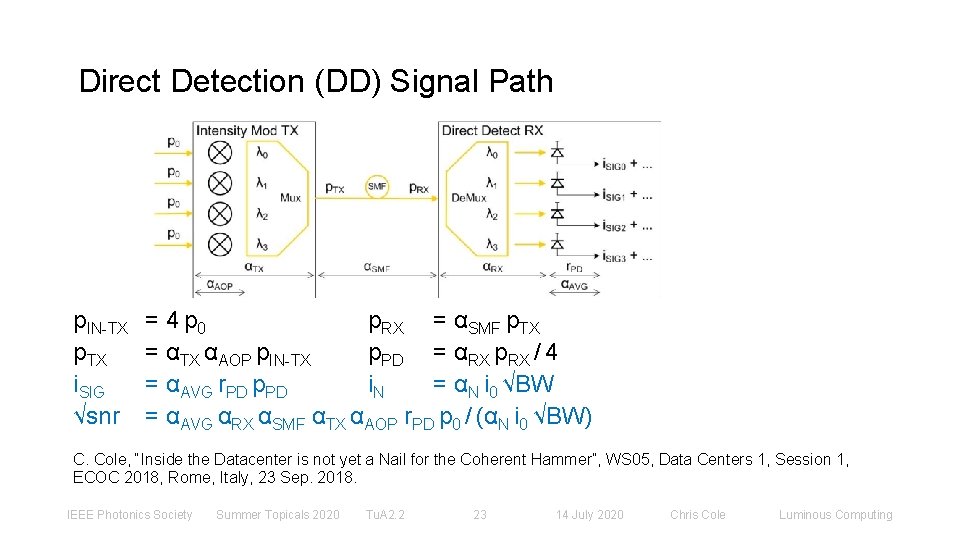
Direct Detection (DD) Signal Path p. IN-TX p. TX i. SIG √snr = 4 p 0 p. RX = αSMF p. TX = αTX αAOP p. IN-TX p. PD = αRX p. RX / 4 = αAVG r. PD p. PD i. N = αN i 0 √BW = αAVG αRX αSMF αTX αAOP r. PD p 0 / (αN i 0 √BW) C. Cole, “Inside the Datacenter is not yet a Nail for the Coherent Hammer”, WS 05, Data Centers 1, Session 1, ECOC 2018, Rome, Italy, 23 Sep. 2018. IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 23 14 July 2020 Chris Cole Luminous Computing
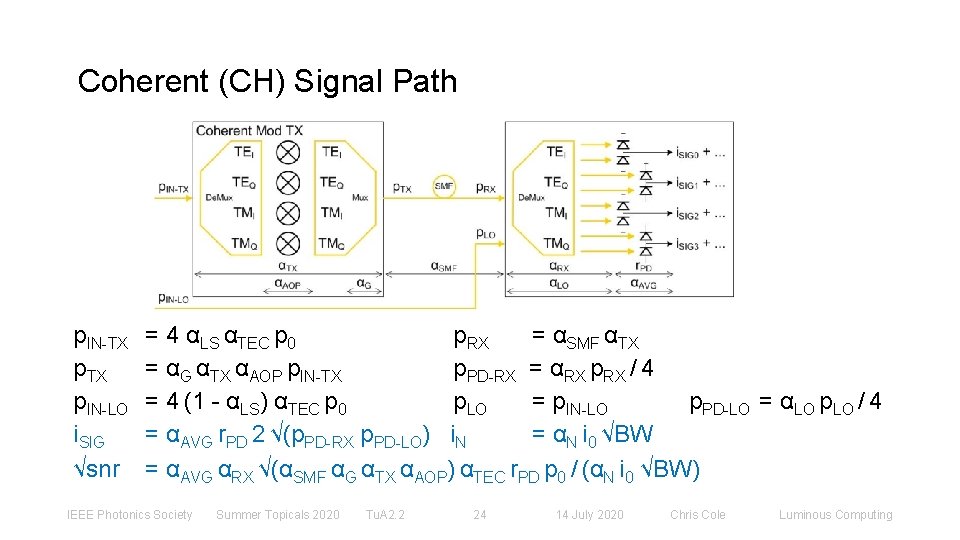
Coherent (CH) Signal Path p. IN-TX p. IN-LO i. SIG √snr = 4 αLS αTEC p 0 p. RX = αSMF αTX = αG αTX αAOP p. IN-TX p. PD-RX = αRX p. RX / 4 = 4 (1 - αLS) αTEC p 0 p. LO = p. IN-LO p. PD-LO = αLO p. LO / 4 = αAVG r. PD 2 √(p. PD-RX p. PD-LO) i. N = αN i 0 √BW = αAVG αRX √(αSMF αG αTX αAOP) αTEC r. PD p 0 / (αN i 0 √BW) IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 24 14 July 2020 Chris Cole Luminous Computing
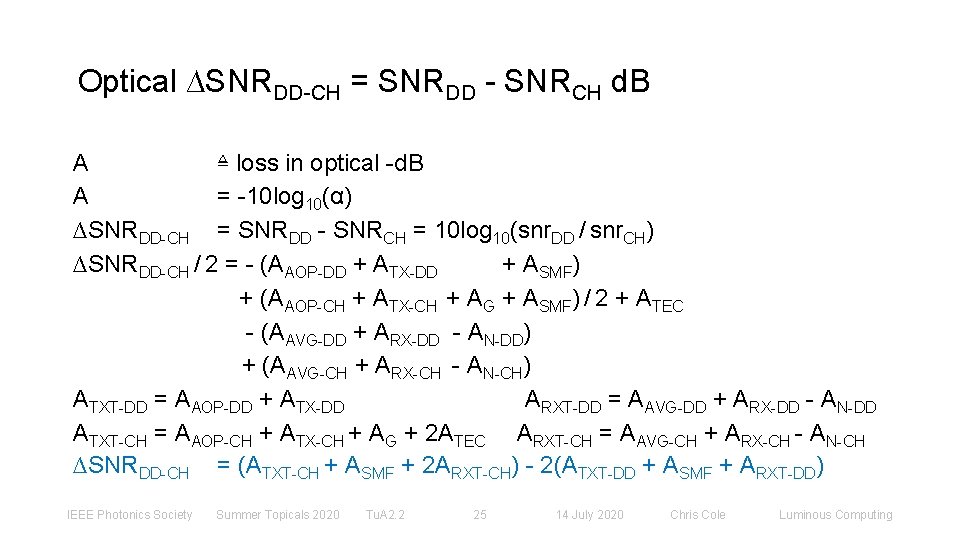
Optical ∆SNRDD-CH = SNRDD - SNRCH d. B A ≜ loss in optical -d. B A = -10 log 10(α) ∆SNRDD-CH = SNRDD - SNRCH = 10 log 10(snr. DD / snr. CH) ∆SNRDD-CH / 2 = - (ΑAOP-DD + ΑTX-DD + ΑSMF) + (ΑAOP-CH + ΑTX-CH + AG + ΑSMF) / 2 + ΑTEC - (ΑAVG-DD + ΑRX-DD - AN-DD) + (ΑAVG-CH + ΑRX-CH - AN-CH) ATXT-DD = ΑAOP-DD + ΑTX-DD ARXT-DD = ΑAVG-DD + ΑRX-DD - AN-DD ATXT-CH = ΑAOP-CH + ΑTX-CH + AG + 2ΑTEC ARXT-CH = ΑAVG-CH + ΑRX-CH - AN-CH ∆SNRDD-CH = (ATXT-CH + ASMF + 2 ARXT-CH) - 2(ATXT-DD + ASMF + ARXT-DD) IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 25 14 July 2020 Chris Cole Luminous Computing

Optical ∆SNRDD-CH d. B Examples • Equal laser input AOP (TEC ignored): ∆SNRDD-CH = ((ATXT-CH + ASMF) - 2(ATXT-DD + ASMF)) + 2(ARXT-CH - ARXT-DD) • 100 G EML NRZ CWDM 4 IMDD vs 100 G Si. PIC QPSK Coherent • Ex. 1: 4 d. B Link Loss (2 km, typical intra datacenter) ∆SNRDD-CH = ((17 + 4) - 2( 5 + 4)) + 2( 4 - 2) = 7 d. B • Ex. 2: 11 d. B Link Loss (20 km, or 2 km & one 7 d. B loss optical switch) ∆SNRDD-CH = ((17 + 11) - 2( 5 + 11)) + 2( 4 - 2) = 0 • Ex. 2: 18 d. B Link Loss (40 km, or 2 km & two 7 d. B loss optical switches) ∆SNRDD-CH IEEE Photonics Society = ((17 + 18) - 2( 5 + 18)) + 2( 4 - 2) Summer Topicals 2020 Tu. A 2. 2 26 14 July 2020 = -7 d. B Chris Cole Luminous Computing

Outline • • • NRZ vs HOM Serial vs WDM Coherent in Telecom Coherent in Datacom IMDD vs Coherent SNR • Intra Datacenter Optics • Appendices IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 27 14 July 2020 Chris Cole Luminous Computing

Intra Datacenter Optics Requirements • What’s important? • Cheap laser(s) • Cheap SNR (low loss components) • Cheap assembly and packaging • Cheap testing • What does Coherent offer? • Expensive Laser • High loss components • Best case comparable packaging cost to IMDD • Complex testing IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 28 14 July 2020 Chris Cole Luminous Computing

TX Modulator Size Comparison • IMDD In. P EML length: • 400 - 500 um (EA 120 um) • Coherent Si MZM length: • 2 - 4 mm • 4 channel Coherent to IMDD TX area ratio: • 10 - 20 x IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 29 Teriphic project, 4 x 100 G PAM 4 EML TX 14 July 2020 Chris Cole Luminous Computing

Intra Datacenter Optics Today: Pluggable • Characteristics • $1 - $2/Gb • ~30 p. J/bit • IMDD DML or EML uncooled TX • 4λ CWDM NRZ or PAM 4 • Link budget: 4 d. B • IMDD vs. Coherent SNR, equal laser DC Power (TEC included): 100 G EML NRZ CWDM 4 IMDD vs 100 G Si. PIC QPSK Coherent ∆SNRDD-CH = 11. 5 d. B (same result for PAM 4 IMDD vs QAM 16 Coherent) IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 30 14 July 2020 Chris Cole Luminous Computing

Intra Datacenter Optics Tomorrow: Co-packaged • Requirements • Co-packaged with Ethernet Switch ASIC • 256 - 512 data lanes • <$1/Gb • <10 p. J/bit • Link budget: 4 d. B • IMDD vs. Coherent SNR, equal laser DC Power (TEC included): 100 G Si. PIC NRZ CWDM 4 IMDD vs 100 G Si. PIC QPSK Coherent ∆SNRDD-CH = 1. 5 d. B (same result for PAM 4 IMDD vs QAM 16 Coherent) IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 31 14 July 2020 Chris Cole Luminous Computing

Summary • Coherent advantages in Transport are unimportant in Intra Datacenter • Coherent indefinitely locks in the cost and power of ADCs and DSPs • This is what PAM 4 did for >100 G Ethernet optics • Good for IC vendors, bad for everyone else as optics improve • “Serial is always cheaper” is a myth for leading data rates • 10 Gb. E was the last time it was true • 1λ Coherent is higher cost and power than 4λ IMDD • Coherent does not reduce the cost and power of short reach optics • There is no IMDD vs Coherent competition for Intra Datacenter links • Coherent is not even on the battleground IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 32 14 July 2020 Chris Cole Luminous Computing

IMDD vs Coherent Thank You www. ieee-sum. org IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 33 14 July 2020 Chris Cole Luminous Computing

Outline • • • NRZ vs HOM Serial vs WDM Coherent in Telecom Coherent in Datacom IMDD vs Coherent SNR Intra Datacenter Optics • Appendix 1 IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 34 14 July 2020 Chris Cole Luminous Computing

Direct Detection (DD) Signal Path Variables p 0 p. IN-TX αAOP αTX p. TX αSMF p. RX αRX p. PD r. PD αAVG ≜ Input POP (Peak Optical Power) reference ≜ TX input POP = AOP (Average OP) if CW ≜ TX POP to AOP modulation loss vs. er (extinction ratio) ≜ TX path intrinsic loss at modulator bias point ≜ TX total output AOP ≜ Link total power loss (connectors, SMF, other passives) ≜ RX total input AOP ≜ RX path intrinsic loss ≜ RX PD input AOP ≜ RX PD responsivity ≜ PD AOP to average electrical signal power loss vs. er IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 35 14 July 2020 Chris Cole Luminous Computing

Direct Detection (DD) SNR i. SIG ≜ RX PD signal current = αAVG r. PD p. PD = αAVG αRX αSMF αTX αAOP r. PD p 0 i. N i 0 αN BW i. N ≜ RX input referred noise current; all sources ≜ RX input noise current density reference ≜ RX input noise current loss vs. i 0 ≜ RX input noise bandwidth = αN i 0 √BW snr √snr = (i. SIG / i. N)2 = αAVG αRX αSMF αTX αAOP r. PD p 0 / (αN i 0 √BW) IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 36 14 July 2020 Chris Cole Luminous Computing

Coherent (CH) Signal Path Variables p 0 αTEC αLS p. IN-TX αAOP αTX αG p. TX αSMF ≜ Input POP (Peak Optical Power) reference ≜ Input POP loss due to laser TEC current ≜ TX input POP loss due to (1 - αLS) LO (Local Oscillator) input split ≜ TX input POP = AOP since CW ≜ TX POP to AOP modulation loss vs. MD (mod. drive) ≜ TX path intrinsic loss at modulator bias point ≜ TX optical gain (αG = 1 if no amplification) ≜ TX total output AOP ≜ Link total power loss (connectors, SMF, other passives) IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 37 14 July 2020 Chris Cole Luminous Computing

Coherent (CH) Signal Path Variables, cont. p. RX p. LO Ф(t) αRX αLO p. PD r. PD αAVG ≜ RX total input AOP ≜ RX LO input AOP ≜ Phase angle between p. RX and p. LO electric fields ≜ RX SIG path intrinsic loss ≜ RX LO path intrinsic loss ≜ RX PD input AOP ≜ RX PD responsivity ≜ PD AOP to average electrical signal power loss vs. MD IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 38 14 July 2020 Chris Cole Luminous Computing

Coherent Signal Addition Optical signals, with same polarization state, add in the electric field domain ELO / √Z ERX / √Z EPD / √Z PPD p. RX p. LO RIN p. PD IEEE Photonics Society ≜ √p. LO = cos Ф(t) √p. RX + j sin Ф(t) √p. RX = √p. LO + cos Ф(t) √p. RX + j sin Ф(t) √p. RX = (√p. LO + cos Ф(t) √p. RX)2 + (sin Ф(t) √p. RX)2 = p. LO + 2 √p. LO √p. RX cos Ф(t) + p. RX << 2 √p. LO √p. RX cos Ф(t) = 2 √(p. LO p. RX) cos Ф(t) Summer Topicals 2020 Tu. A 2. 2 39 14 July 2020 Chris Cole Luminous Computing

Coherent (CH) SNR i. SIG ≜ RX balanced PD pair signal current i. SIG = αAVG r. PD 2 √(p. PD-RX p. PD-LO) cos Ф(t) ≜ 1 αLS ≜ ½ αLO ≜ αRX i. SIG = αAVG αRX √(αSMF αG αTX αAOP) αTEC r. PD p 0 i. N i 0 αN BW i. N ≜ RX input referred noise current; all sources ≜ RX input noise current density reference ≜ RX input noise current loss vs. i 0 ≜ RX input noise bandwidth = αN i 0 √BW snr √snr = (i. SIG / i. N)2 = αAVG αRX √(αSMF αG αTX αAOP) αTEC r. PD p 0 / (αN i 0 √BW) IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 40 14 July 2020 Chris Cole Luminous Computing

Ratio DD SNR to CH SNR: √(snr. DD / snr. CH) √snr. DD = αAVG αRX αSMF αTX αAOP r. PD p 0 / (αN i 0 √BW) √snr. CH = αAVG αRX √(αSMF αG αTX αAOP) αTEC r. PD p 0 / (αN i 0 √BW) r. PD-DD ≜ r. PD-CH BWDD ≜ BWCH √(snr. DD / snr. CH) = αAVG-DD αRX-DD αSMF αTX-DD αAOP-DD αN-CH / αAVG-CH αRX-CH √(αSMF αG αTX-CH αAOP-CH) αTEC αN-DD IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 41 14 July 2020 Chris Cole Luminous Computing
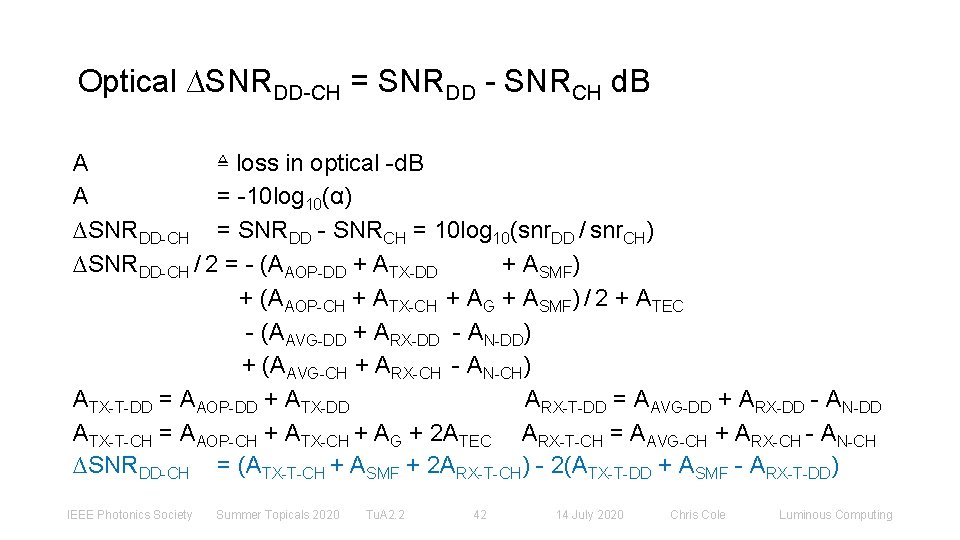
Optical ∆SNRDD-CH = SNRDD - SNRCH d. B A ≜ loss in optical -d. B A = -10 log 10(α) ∆SNRDD-CH = SNRDD - SNRCH = 10 log 10(snr. DD / snr. CH) ∆SNRDD-CH / 2 = - (ΑAOP-DD + ΑTX-DD + ΑSMF) + (ΑAOP-CH + ΑTX-CH + AG + ΑSMF) / 2 + ΑTEC - (ΑAVG-DD + ΑRX-DD - AN-DD) + (ΑAVG-CH + ΑRX-CH - AN-CH) ATX-T-DD = ΑAOP-DD + ΑTX-DD ARX-T-DD = ΑAVG-DD + ΑRX-DD - AN-DD ATX-T-CH = ΑAOP-CH + ΑTX-CH + AG + 2ΑTEC ARX-T-CH = ΑAVG-CH + ΑRX-CH - AN-CH ∆SNRDD-CH = (ATX-T-CH + ASMF + 2 ARX-T-CH) - 2(ATX-T-DD + ASMF - ARX-T-DD) IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 42 14 July 2020 Chris Cole Luminous Computing

Outline • • • NRZ vs HOM Serial vs WDM Coherent in Telecom Coherent in Datacom IMDD vs Coherent SNR Intra Datacenter Optics • Appendix 2 IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 43 14 July 2020 Chris Cole Luminous Computing
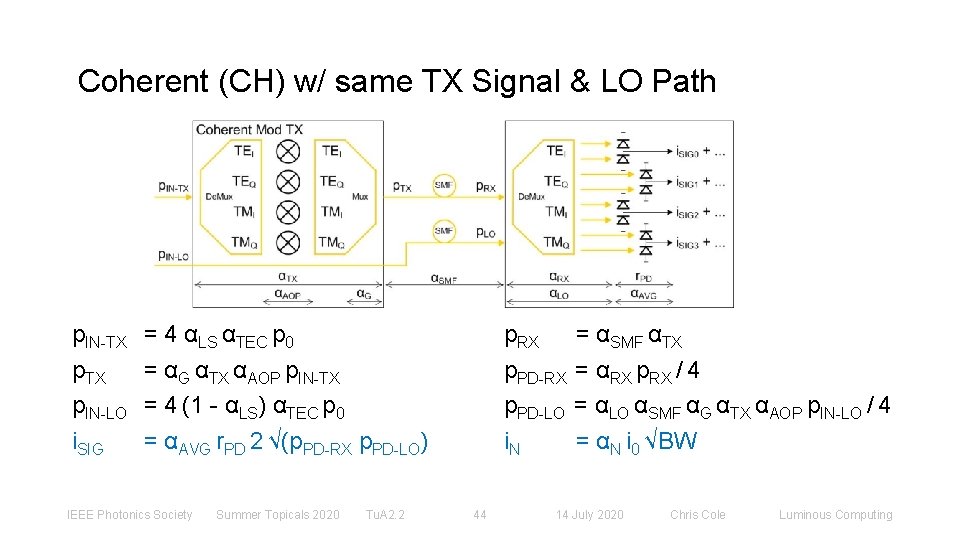
Coherent (CH) w/ same TX Signal & LO Path p. IN-TX p. IN-LO i. SIG = 4 αLS αTEC p 0 = αG αTX αAOP p. IN-TX = 4 (1 - αLS) αTEC p 0 = αAVG r. PD 2 √(p. PD-RX p. PD-LO) IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 p. RX p. PD-LO i. N 44 = αSMF αTX = αRX p. RX / 4 = αLO αSMF αG αTX αAOP p. IN-LO / 4 = αN i 0 √BW 14 July 2020 Chris Cole Luminous Computing

Coherent (CH) RX Signal w/ same TX Signal & LO Path i. SIG ≜ RX balanced PD pair signal current i. SIG αLS ≜ ½ i. SIG = αAVG r. PD 2 √(p. PD-RX p. PD-LO) αLO ≜ αRX = αAVG αRX αSMF αG αTX αAOP αTEC r. PD p 0 Equal DD and CH total input AOP condition: p. IN-DD-TX ≜ p. IN-CH-TX + p. IN-CH-LO i. DD-SIG = i. CH-SIG When the LO is remote, i. e. it’s a RO, there is no Coherent signal gain! Same TX Signal and LO Path analysis approach proposed by Mike Frankel, Ciena, 18 Jan 2018. IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 45 14 July 2020 Chris Cole Luminous Computing

Outline • • • NRZ vs HOM Serial vs WDM Coherent in Telecom Coherent in Datacom IMDD vs Coherent SNR Intra Datacenter Optics • Appendix 3 IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 46 14 July 2020 Chris Cole Luminous Computing

∆SNRDD-CH = SNRDD - SNRCH Examples ∆SNRDD-CH / 2 = IEEE Photonics Society - ΑAOP-DD + ΑAOP-CH / 2 // TX - ΑTX-DD + ΑTX-CH / 2 // TX - (- ΑG / 2) + ΑTEC // TX Scenario - ΑSMF + ΑSMF / 2 // Link - ΑRX-DD + ΑRX-CH // RX - ΑAVG-DD + ΑAVG-CH // RX - (- AN-DD) + (- AN-CH) // RX Summer Topicals 2020 Tu. A 2. 2 47 14 July 2020 Chris Cole Luminous Computing

TX Modulation Loss § αAOP, AAOP ≜ TX input POP to AOP modulation loss; linear, -d. B § αAOP-NRZ [er] = (er + 1) / (2 er) // Mod. TX αAOP-NRZ [er] =1 // DML TX αAOP-PAM 4 [er] = (er + 1) / (2 er) // Mod. TX αAOP-PAM 4 [er] =1 // DML TX § αAOP-QPSK [2 Vπ] = 1 αAOP-QPSK [Vπ] = 1/2 αAOP-QAM 16 [2 Vπ] = 5/9 αAOP-QAM 16 [Vπ] = 5/18 § Equal DD & CH TX modulation drive MDDD-Max ≜ ½ MDCH-Max MDCH = Vπ IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 48 14 July 2020 Chris Cole Luminous Computing
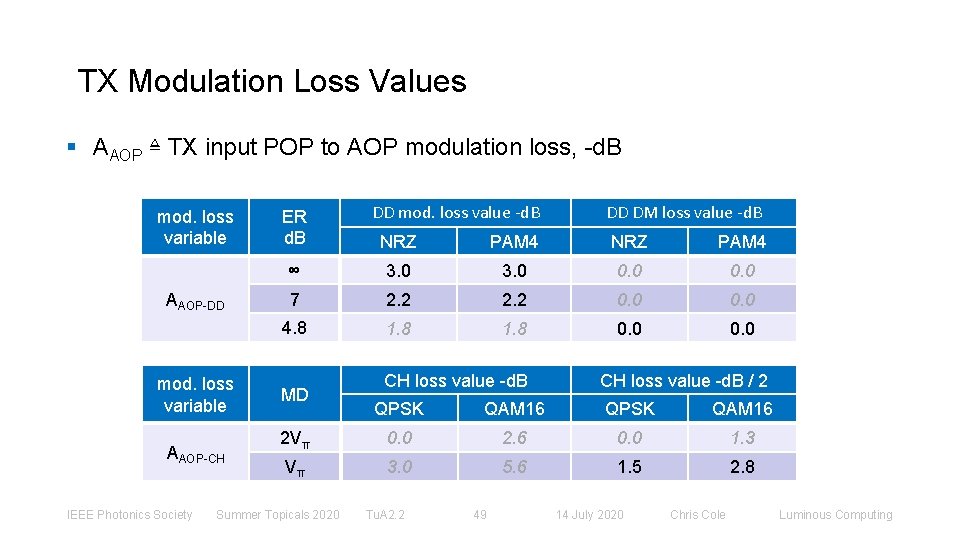
TX Modulation Loss Values § AAOP ≜ TX input POP to AOP modulation loss, -d. B mod. loss variable AAOP-DD mod. loss variable AAOP-CH IEEE Photonics Society ER d. B DD mod. loss value -d. B DD DM loss value -d. B NRZ PAM 4 ∞ 3. 0 0. 0 7 2. 2 0. 0 4. 8 1. 8 0. 0 MD CH loss value -d. B / 2 QPSK QAM 16 2 Vπ 0. 0 2. 6 0. 0 1. 3 Vπ 3. 0 5. 6 1. 5 2. 8 Summer Topicals 2020 Tu. A 2. 2 49 14 July 2020 Chris Cole Luminous Computing
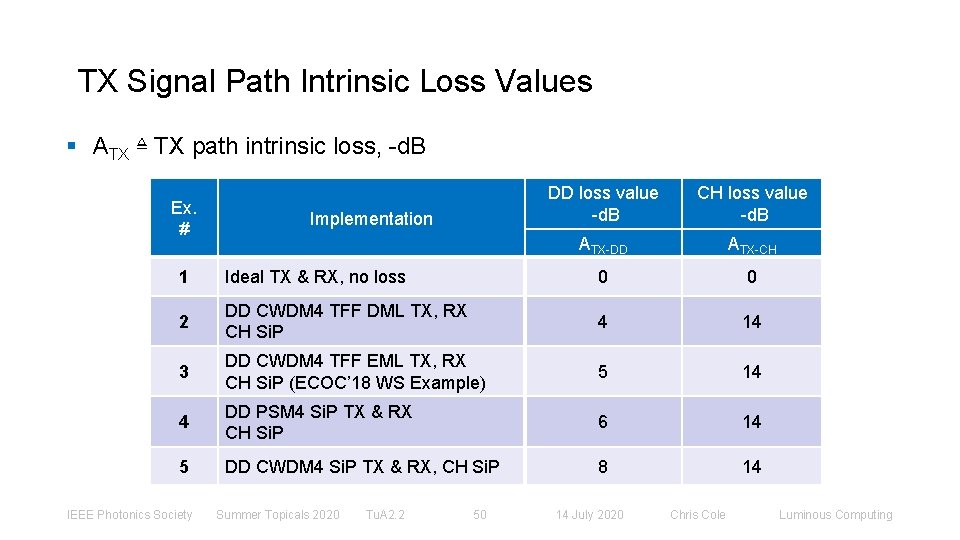
TX Signal Path Intrinsic Loss Values § ATX ≜ TX path intrinsic loss, -d. B Ex. # Implementation DD loss value -d. B CH loss value -d. B ATX-DD ATX-CH 1 Ideal TX & RX, no loss 0 0 2 DD CWDM 4 TFF DML TX, RX CH Si. P 4 14 3 DD CWDM 4 TFF EML TX, RX CH Si. P (ECOC’ 18 WS Example) 5 14 4 DD PSM 4 Si. P TX & RX CH Si. P 6 14 5 DD CWDM 4 Si. P TX & RX, CH Si. P 8 14 IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 50 14 July 2020 Chris Cole Luminous Computing

TX Scenarios § αTEC, ATEC ≜ TXCH input POP loss, laser TEC current; linear, -d. B § αG , A G ≜ TXCH optical gain ΑG TXCH optical gain = - ΑG TXDD optical loss in ∆SNRDD-CH table § Scenario 1: equal laser DC power (40% efficient CH TEC) i. Laser-bias-DD ≜ i. Laser-bias-CH + i. Laser-TEC-CH αTEC ≜ 0. 4 αG ≜ 1 § Scenario 2: equal TX & LO total input POP (no CH TEC) p. IN-TX-DD ≜ p. IN-TX-CH + p. IN-LO-CH αTEC ≜ 1 αG ≜ 1 IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 51 14 July 2020 Chris Cole Luminous Computing

TX Scenarios, cont. § Scenario 3: equal TX total output AOP (no DC power limit) p. TX-DD ≜ p. TX-CH A TX-DD + A AOP-DD = AG + ATX-CH + AAOP-CH + ALS + ATEC αTEC ≜ 1 ATEC =0 αLS ≜ 1/2 ALS =3 - AG / 2 = ((ATX-CH + AAOP-CH + 3) - (ATX-DD + AAOP-DD)) / 2 IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 52 14 July 2020 Chris Cole Luminous Computing
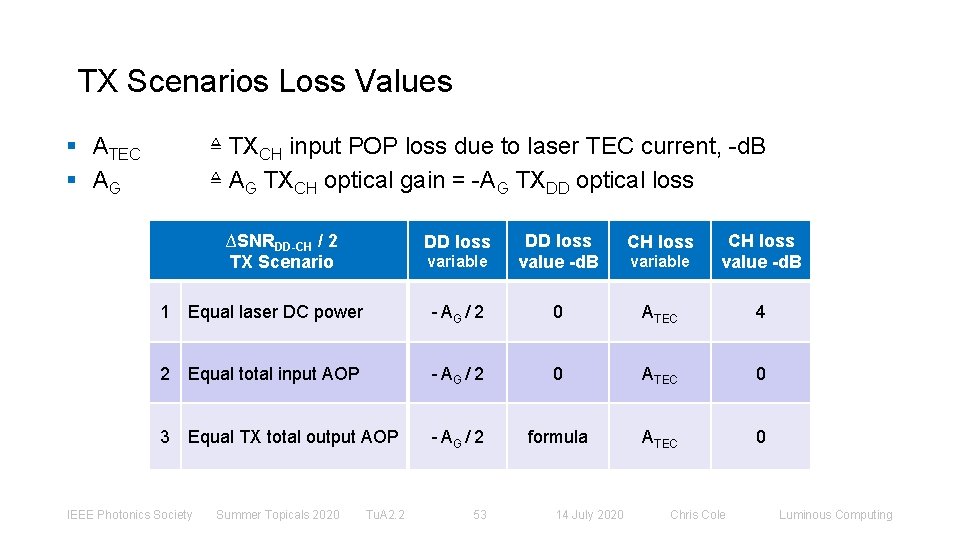
TX Scenarios Loss Values § ATEC § AG ≜ TXCH input POP loss due to laser TEC current, -d. B ≜ AG TXCH optical gain = -AG TXDD optical loss ∆SNRDD-CH / 2 TX Scenario CH loss variable DD loss value -d. B variable CH loss value -d. B DD loss 1 Equal laser DC power - ΑG / 2 0 ΑTEC 4 2 Equal total input AOP - ΑG / 2 0 ΑTEC 0 3 Equal TX total output AOP - ΑG / 2 formula ΑTEC 0 IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 53 14 July 2020 Chris Cole Luminous Computing

Link Loss Values § ASMF ≜ Link total power loss (connectors, SMF, other passives), -d. B § Standard datacenter link loss budget ASMF ≜ 4 DD loss value -d. B CH loss value -d. B ASMF / 2 4. 0 2. 0 IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 54 14 July 2020 Chris Cole Luminous Computing
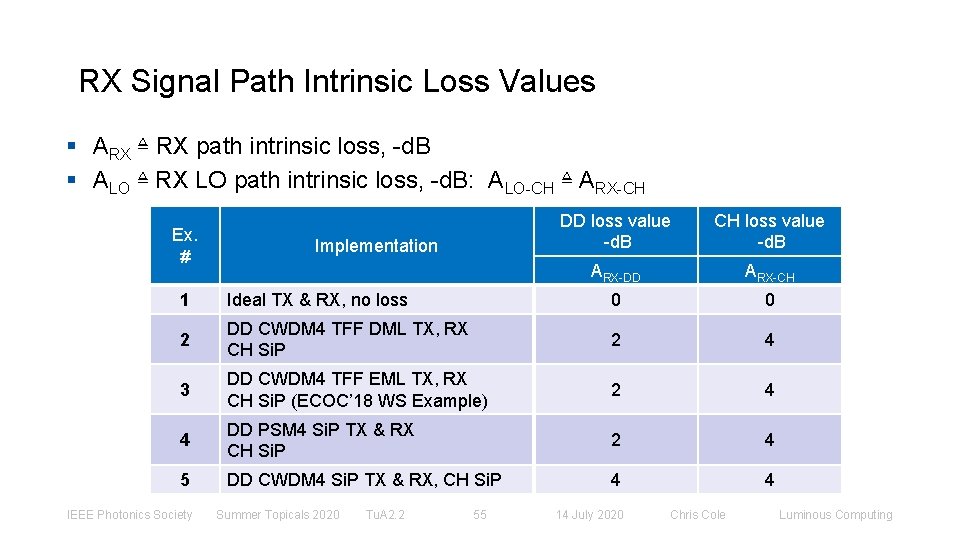
RX Signal Path Intrinsic Loss Values § ARX ≜ RX path intrinsic loss, -d. B § ALO ≜ RX LO path intrinsic loss, -d. B: ALO-CH ≜ ARX-CH Ex. # Implementation DD loss value -d. B CH loss value -d. B ARX-DD ARX-CH 1 Ideal TX & RX, no loss 0 0 2 DD CWDM 4 TFF DML TX, RX CH Si. P 2 4 3 DD CWDM 4 TFF EML TX, RX CH Si. P (ECOC’ 18 WS Example) 2 4 4 DD PSM 4 Si. P TX & RX CH Si. P 2 4 5 DD CWDM 4 Si. P TX & RX, CH Si. P 4 4 IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 55 14 July 2020 Chris Cole Luminous Computing

RX Modulation Loss § αAVG, AAVG ≜ RX PD AOP to average electrical signal power loss; linear, -d. B § αLS ≜ TX input POP loss due to (1 - αLS) split with LO input § αAVG-NRZ [er] = (er – 1) / (er + 1) αAVG-PAM 4 [er] = √(5/9) (er – 1) / (er + 1) § αAVG-QPSK [2 Vπ] = 1 αAVG-QPSK [Vπ] =1 αAVG-QAM 16 [2 Vπ] = 1 αAVG-QAM 16 [Vπ] = 1 § Equal DD & CH TX modulation drive MDDD-Max ≜ ½ MDCH-Max MDCH = Vπ IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 56 14 July 2020 Chris Cole Luminous Computing
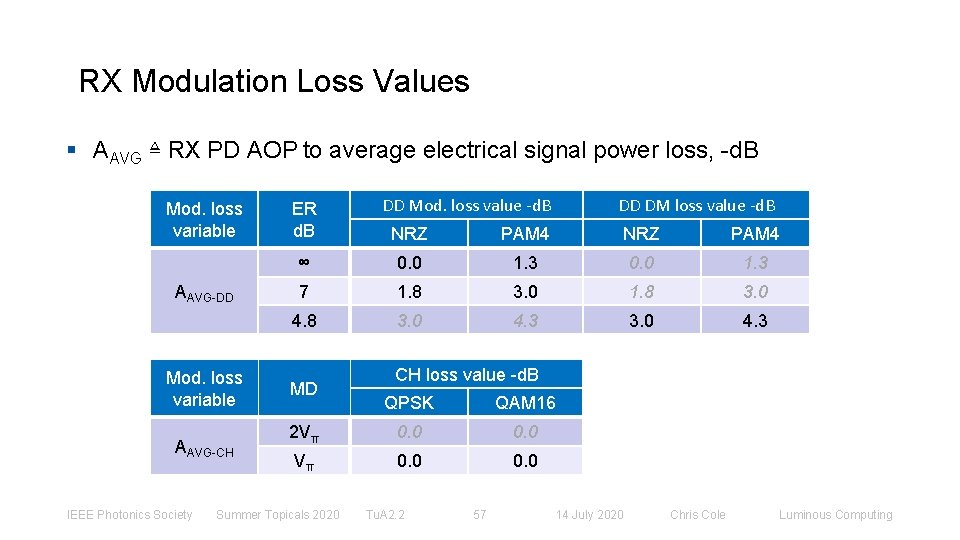
RX Modulation Loss Values § AAVG ≜ RX PD AOP to average electrical signal power loss, -d. B Mod. loss variable AAVG-DD Mod. loss variable AAVG-CH IEEE Photonics Society ER d. B DD Mod. loss value -d. B DD DM loss value -d. B NRZ PAM 4 ∞ 0. 0 1. 3 7 1. 8 3. 0 4. 3 MD CH loss value -d. B QPSK QAM 16 2 Vπ 0. 0 Summer Topicals 2020 Tu. A 2. 2 57 14 July 2020 Chris Cole Luminous Computing

Coherent Unequal SIG/LO Split Loss § αALS, AALS αLS AALS § A’AVG-CH ≜ Unequal SIG/LO split αLS ≠ ½ loss; linear, -d. B = 2 √(αLS (1 - αLS)) ≜ 1/2 =0 ≜ 2/3 = 0. 3 = AAVG-CH + AALS mod. loss variable A’AVG-CH IEEE Photonics Society CH loss value -d. B αLS = 1/2 MD αLS = 2/3 QPSK QAM 16 2 Vπ 0. 0 0. 3 Summer Topicals 2020 Tu. A 2. 2 58 14 July 2020 Chris Cole Luminous Computing

RX Input Referred Noise Current Loss Values § AN ≜ RX input noise current density loss vs. reference, -d. B § αN i 0 ≜ RX input noise current density § RX input noise current density values αN-DD i 0 = 12 p. A / √Hz αN-DD ≜ 1 i 0 = 12 p. A / √Hz αN-CH i 0 = 20 p. A / √Hz αN-CH = 5/3 IEEE Photonics Society DD loss value -d. B CH loss value -d. B AN-DD AN-CH 0. 0 -2. 2 Summer Topicals 2020 Tu. A 2. 2 59 14 July 2020 Chris Cole Luminous Computing
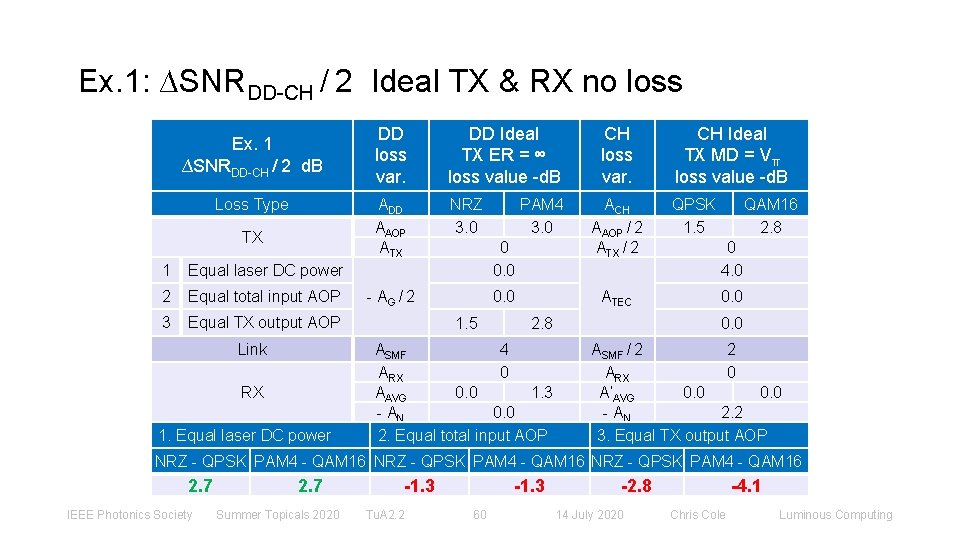
Ex. 1: ∆SNRDD-CH / 2 Ideal TX & RX no loss Ex. 1 ∆SNRDD-CH / 2 d. B Loss Type TX 1 Equal laser DC power 2 Equal total input AOP 3 Equal TX output AOP Link RX 1. Equal laser DC power DD loss var. DD Ideal TX ER = ∞ loss value -d. B ADD ΑAOP ΑTX NRZ 3. 0 PAM 4 3. 0 0 0. 0 - ΑG / 2 1. 5 CH loss var. ACH ΑAOP / 2 ΑTX / 2 ATEC 2. 8 ΑSMF 4 ΑRX 0 ΑAVG 0. 0 1. 3 - AN 0. 0 2. Equal total input AOP CH Ideal TX MD = Vπ loss value -d. B QPSK 1. 5 QAM 16 2. 8 0 4. 0 0. 0 ΑSMF / 2 2 ΑRX 0 Α’AVG 0. 0 - AN 2. 2 3. Equal TX output AOP NRZ - QPSK PAM 4 - QAM 16 2. 7 IEEE Photonics Society 2. 7 Summer Topicals 2020 -1. 3 Tu. A 2. 2 -1. 3 60 -2. 8 14 July 2020 -4. 1 Chris Cole Luminous Computing
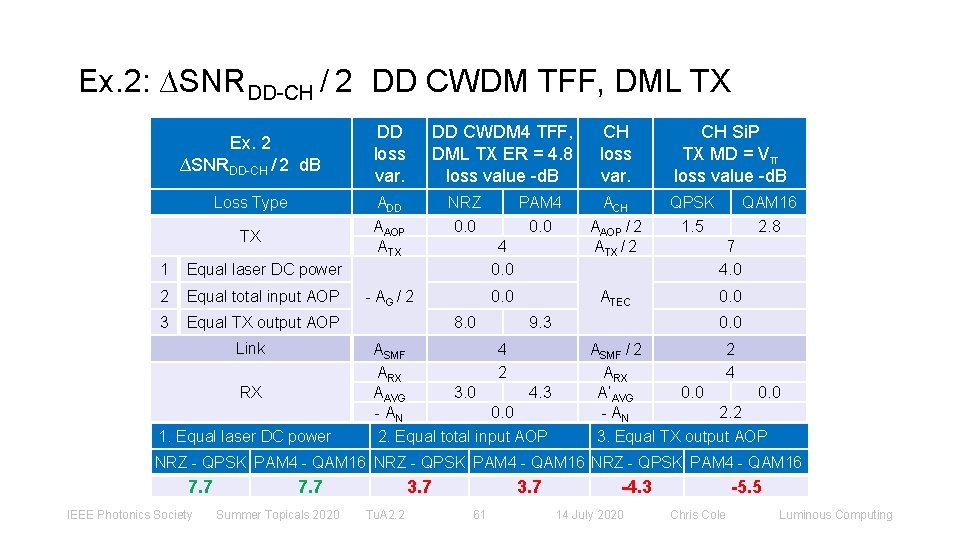
Ex. 2: ∆SNRDD-CH / 2 DD CWDM TFF, DML TX Ex. 2 ∆SNRDD-CH / 2 d. B Loss Type DD loss var. DD CWDM 4 TFF, DML TX ER = 4. 8 loss value -d. B ADD ΑAOP ΑTX TX 1 Equal laser DC power 2 Equal total input AOP 3 Equal TX output AOP Link RX 1. Equal laser DC power NRZ 0. 0 PAM 4 0. 0 - ΑG / 2 8. 0 CH loss var. ACH ΑAOP / 2 ΑTX / 2 ATEC 9. 3 ΑSMF 4 ΑRX 2 ΑAVG 3. 0 4. 3 - AN 0. 0 2. Equal total input AOP CH Si. P TX MD = Vπ loss value -d. B QPSK 1. 5 QAM 16 2. 8 7 4. 0 0. 0 ΑSMF / 2 2 ΑRX 4 Α’AVG 0. 0 - AN 2. 2 3. Equal TX output AOP NRZ - QPSK PAM 4 - QAM 16 7. 7 IEEE Photonics Society 7. 7 Summer Topicals 2020 3. 7 Tu. A 2. 2 3. 7 61 -4. 3 14 July 2020 -5. 5 Chris Cole Luminous Computing
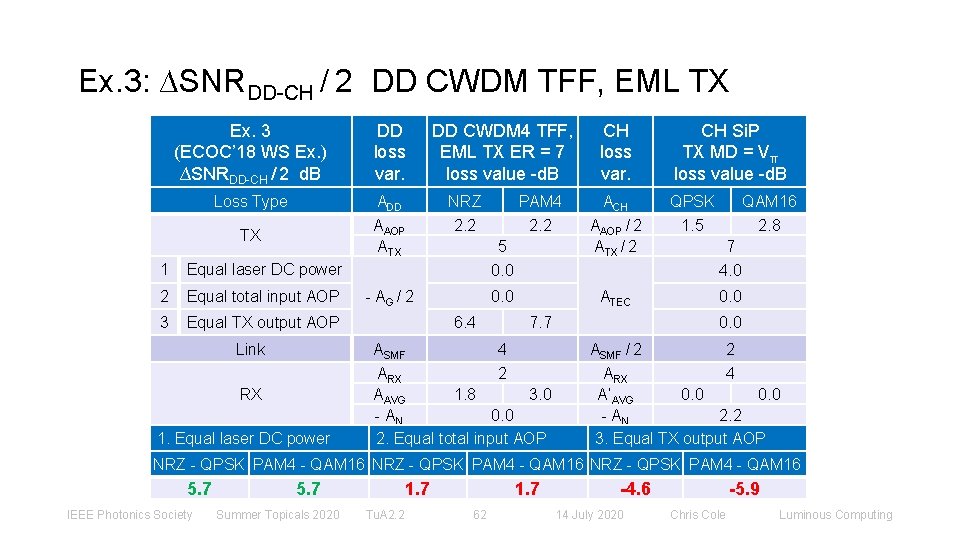
Ex. 3: ∆SNRDD-CH / 2 DD CWDM TFF, EML TX Ex. 3 (ECOC’ 18 WS Ex. ) ∆SNRDD-CH / 2 d. B DD loss var. Loss Type ADD NRZ TX ΑAOP ΑTX 2. 2 1 Equal laser DC power 2 Equal total input AOP 3 Equal TX output AOP Link RX 1. Equal laser DC power DD CWDM 4 TFF, EML TX ER = 7 loss value -d. B CH loss var. CH Si. P TX MD = Vπ loss value -d. B PAM 4 ACH QPSK QAM 16 2. 2 ΑAOP / 2 ΑTX / 2 1. 5 2. 8 5 0. 0 - ΑG / 2 6. 4 ATEC 7. 7 ΑSMF 4 ΑRX 2 ΑAVG 1. 8 3. 0 - AN 0. 0 2. Equal total input AOP 7 4. 0 0. 0 ΑSMF / 2 2 ΑRX 4 Α’AVG 0. 0 - AN 2. 2 3. Equal TX output AOP NRZ - QPSK PAM 4 - QAM 16 5. 7 IEEE Photonics Society 5. 7 Summer Topicals 2020 1. 7 Tu. A 2. 2 1. 7 62 -4. 6 14 July 2020 -5. 9 Chris Cole Luminous Computing
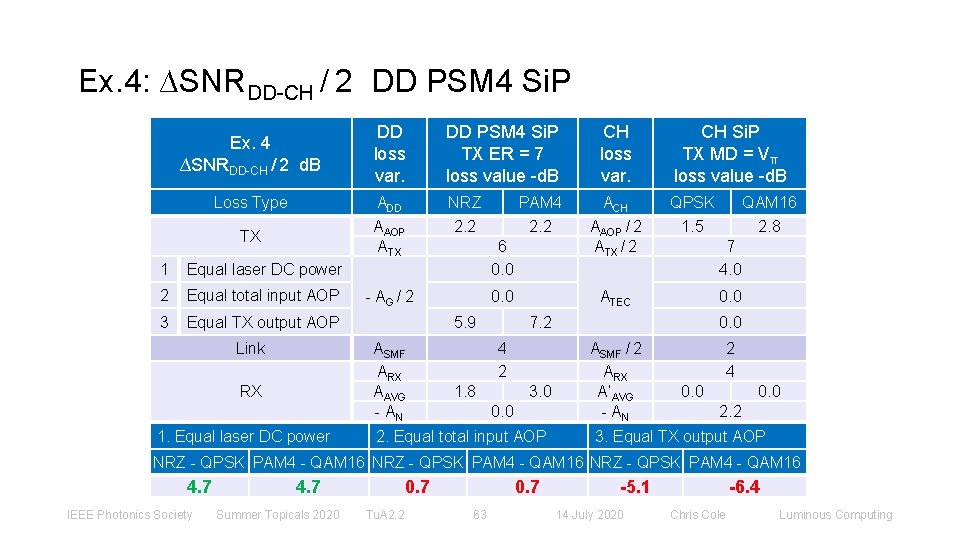
Ex. 4: ∆SNRDD-CH / 2 DD PSM 4 Si. P Ex. 4 ∆SNRDD-CH / 2 d. B Loss Type TX 1 Equal laser DC power 2 Equal total input AOP 3 Equal TX output AOP Link DD loss var. DD PSM 4 Si. P TX ER = 7 loss value -d. B ADD ΑAOP ΑTX NRZ 2. 2 1. Equal laser DC power 6 0. 0 - ΑG / 2 5. 9 ΑSMF ΑRX ΑAVG - AN RX PAM 4 2. 2 CH loss var. ACH ΑAOP / 2 ΑTX / 2 CH Si. P TX MD = Vπ loss value -d. B QPSK 1. 5 7 4. 0 0. 0 ATEC 7. 2 4 2 1. 8 3. 0 0. 0 2. Equal total input AOP QAM 16 2. 8 0. 0 ΑSMF / 2 ΑRX Α’AVG - AN 2 4 0. 0 2. 2 3. Equal TX output AOP NRZ - QPSK PAM 4 - QAM 16 4. 7 IEEE Photonics Society 4. 7 Summer Topicals 2020 0. 7 Tu. A 2. 2 0. 7 63 -5. 1 14 July 2020 -6. 4 Chris Cole Luminous Computing
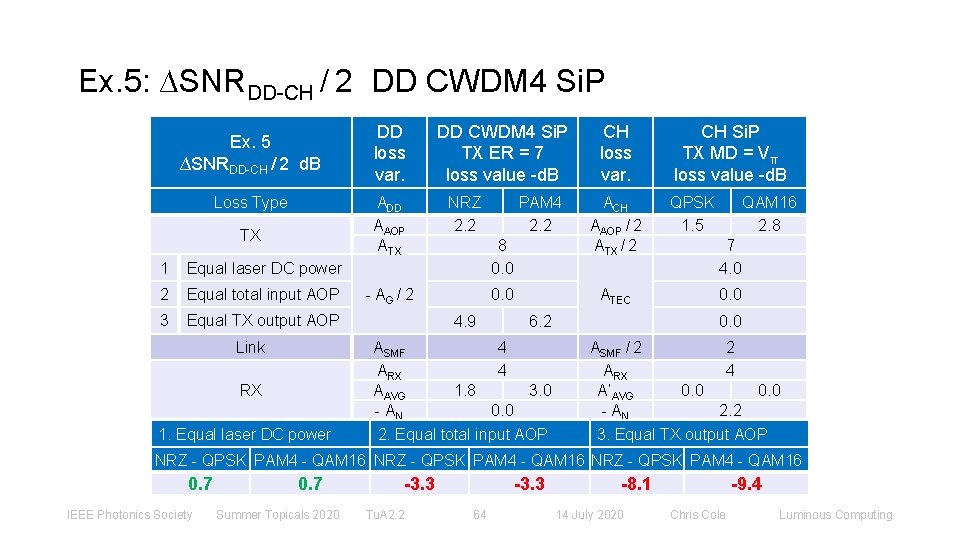
Ex. 5: ∆SNRDD-CH / 2 DD CWDM 4 Si. P Ex. 5 ∆SNRDD-CH / 2 d. B Loss Type DD loss var. ADD ΑAOP ΑTX TX 1 Equal laser DC power 2 Equal total input AOP 3 Equal TX output AOP Link RX 1. Equal laser DC power DD CWDM 4 Si. P TX ER = 7 loss value -d. B NRZ 2. 2 PAM 4 2. 2 8 0. 0 - ΑG / 2 4. 9 CH loss var. ACH ΑAOP / 2 ΑTX / 2 ATEC 6. 2 ΑSMF 4 ΑRX 4 ΑAVG 1. 8 3. 0 - AN 0. 0 2. Equal total input AOP CH Si. P TX MD = Vπ loss value -d. B QPSK 1. 5 QAM 16 2. 8 7 4. 0 0. 0 ΑSMF / 2 2 ΑRX 4 Α’AVG 0. 0 - AN 2. 2 3. Equal TX output AOP NRZ - QPSK PAM 4 - QAM 16 0. 7 IEEE Photonics Society 0. 7 Summer Topicals 2020 -3. 3 Tu. A 2. 2 -3. 3 64 -8. 1 14 July 2020 -9. 4 Chris Cole Luminous Computing
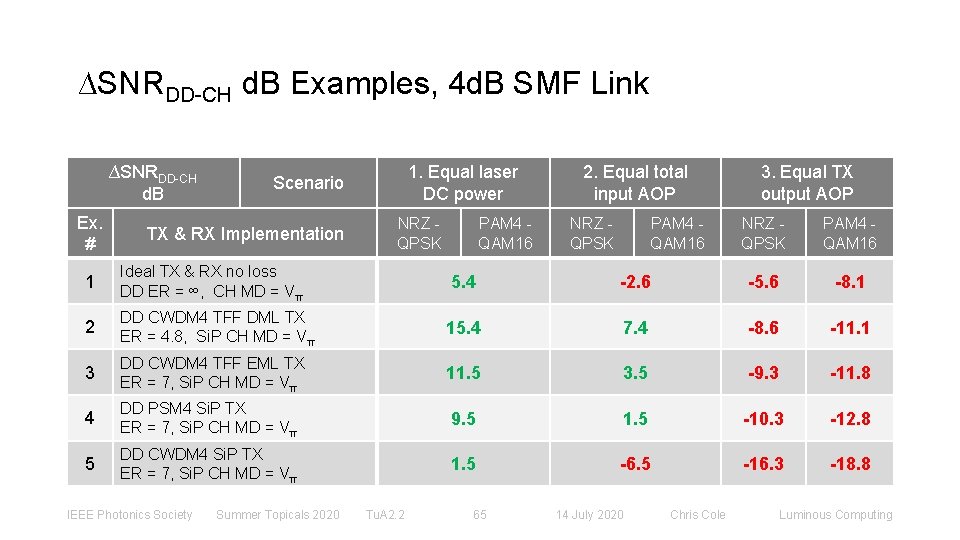
∆SNRDD-CH d. B Examples, 4 d. B SMF Link ∆SNRDD-CH d. B Ex. # 1. Equal laser DC power Scenario TX & RX Implementation 1 Ideal TX & RX no loss DD ER = ∞, CH MD = Vπ 2 NRZ QPSK PAM 4 QAM 16 2. Equal total input AOP NRZ QPSK PAM 4 QAM 16 3. Equal TX output AOP NRZ QPSK PAM 4 QAM 16 5. 4 -2. 6 -5. 6 -8. 1 DD CWDM 4 TFF DML TX ER = 4. 8, Si. P CH MD = Vπ 15. 4 7. 4 -8. 6 -11. 1 3 DD CWDM 4 TFF EML TX ER = 7, Si. P CH MD = Vπ 11. 5 3. 5 -9. 3 -11. 8 4 DD PSM 4 Si. P TX ER = 7, Si. P CH MD = Vπ 9. 5 1. 5 -10. 3 -12. 8 5 DD CWDM 4 Si. P TX ER = 7, Si. P CH MD = Vπ 1. 5 -6. 5 -16. 3 -18. 8 IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 65 14 July 2020 Chris Cole Luminous Computing
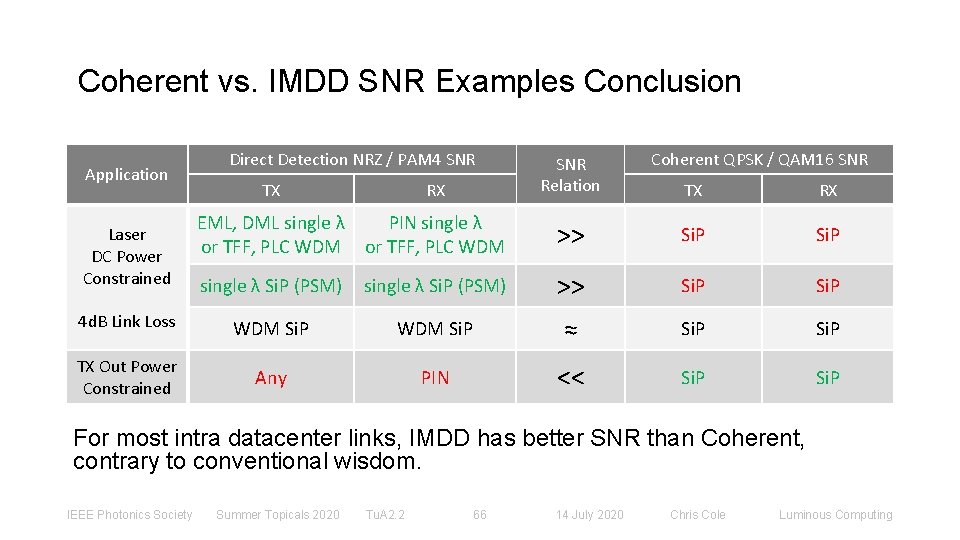
Coherent vs. IMDD SNR Examples Conclusion Direct Detection NRZ / PAM 4 SNR TX RX SNR Relation EML, DML single λ or TFF, PLC WDM PIN single λ or TFF, PLC WDM single λ Si. P (PSM) 4 d. B Link Loss TX Out Power Constrained Application Laser DC Power Constrained Coherent QPSK / QAM 16 SNR TX RX >> Si. P single λ Si. P (PSM) >> Si. P WDM Si. P ≈ Si. P Any PIN << Si. P For most intra datacenter links, IMDD has better SNR than Coherent, contrary to conventional wisdom. IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 66 14 July 2020 Chris Cole Luminous Computing

IMDD vs Coherent Appendices Thank You www. ieee-sum. org IEEE Photonics Society Summer Topicals 2020 Tu. A 2. 2 67 14 July 2020 Chris Cole Luminous Computing
- Slides: 67