Imaging Geometry for the Pinhole Camera Outline Motivation

Imaging Geometry for the Pinhole Camera Outline: • Motivation • |The pinhole camera Unis, 3 Oct 2005 1

Example 1: Self-Localisation View 3 View 1 View 2 Unis, 3 Oct 2005 2

Example 2: Build a Panorama (register many images into a common frame) Unis, 3 Oct 2005 M. Brown and D. G. Lowe. Recognising Panoramas. ICCV 2003 3

Example 3: 3 D Reconstruction: Detect Correspondences and triangulate Unis, 3 Oct 2005 4

Example 4: Camera motion tracking ⇒ image stabilization background part of the image registered original Unis, 3 Oct 2005 stabilized 5

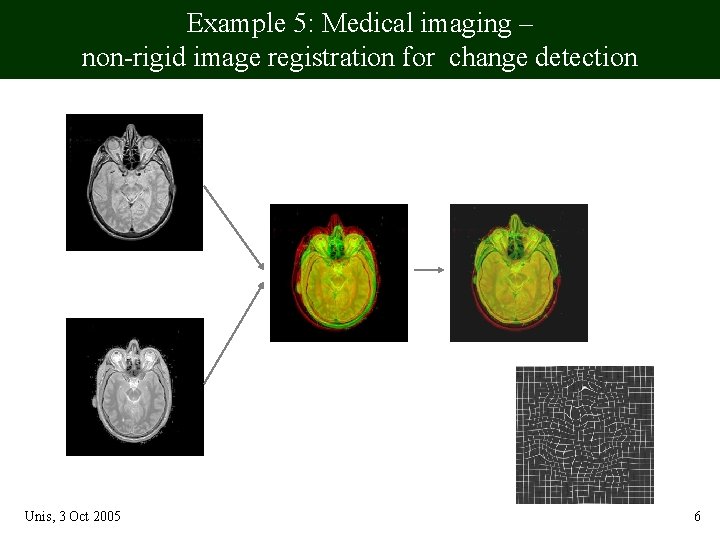
Example 5: Medical imaging – non-rigid image registration for change detection from the atlas before registration after test slice Unis, 3 Oct 2005 deform. field 6

Example 6: Recognition and Localisation of Objects • Object Models: Unis, 3 Oct 2005 • What objects are in the image? • Where are they? 7

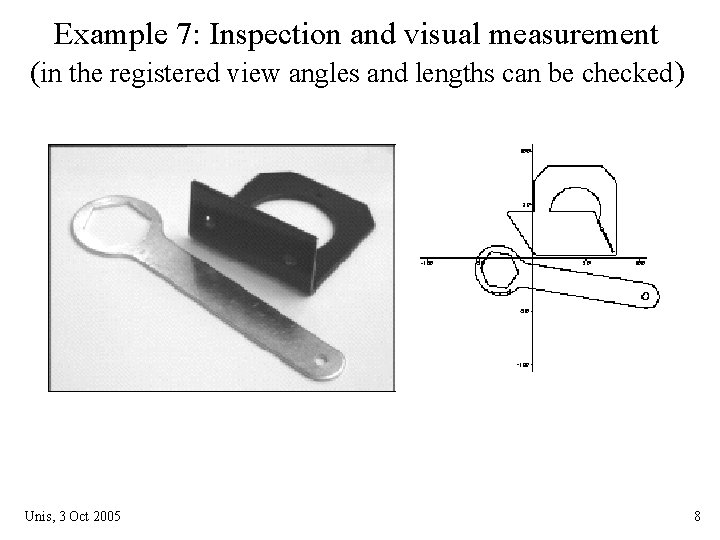
Example 7: Inspection and visual measurement (in the registered view angles and lengths can be checked) Unis, 3 Oct 2005 8

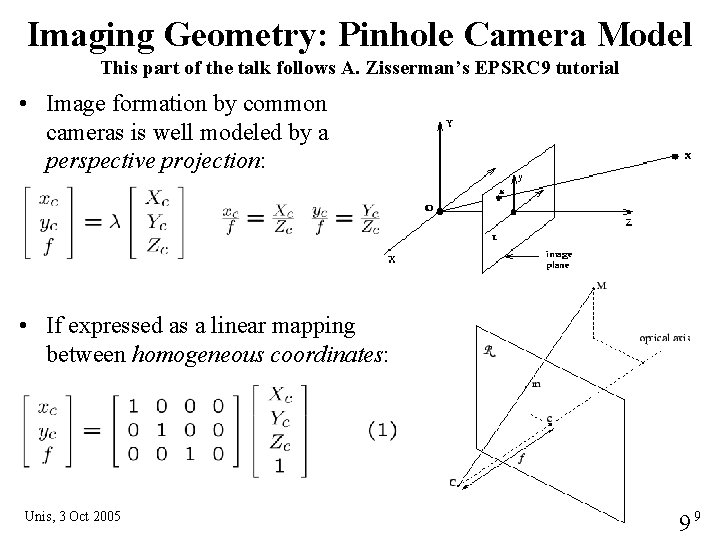
Imaging Geometry: Pinhole Camera Model This part of the talk follows A. Zisserman’s EPSRC 9 tutorial • Image formation by common cameras is well modeled by a perspective projection: • If expressed as a linear mapping between homogeneous coordinates: Unis, 3 Oct 2005 99

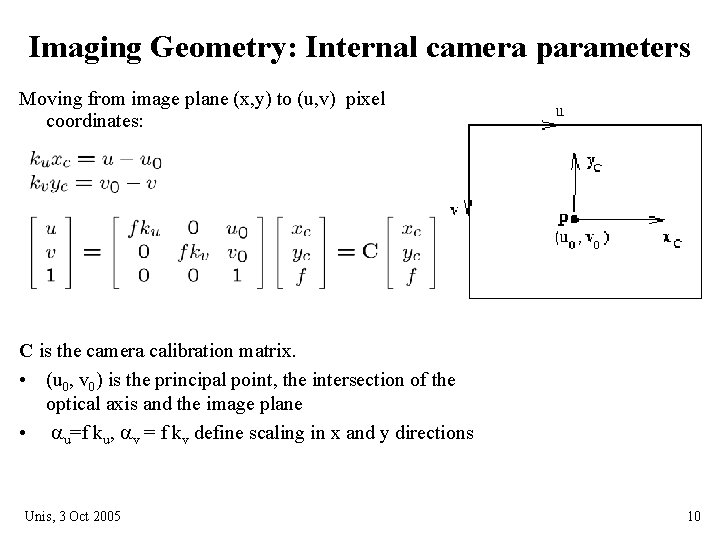
Imaging Geometry: Internal camera parameters Moving from image plane (x, y) to (u, v) pixel coordinates: C is the camera calibration matrix. • (u 0, v 0) is the principal point, the intersection of the optical axis and the image plane • au=f ku, av = f kv define scaling in x and y directions Unis, 3 Oct 2005 10

Imaging Geometry: From World to Camera Coordinates The Euclidean transformation (rigid motion of the camera) is described by Xc = R Xw + T. Chaining all the transformations: This defines a 3 x 4 projection matrix P from Euclidean 3 -space to an image: Unis, 3 Oct 2005 11

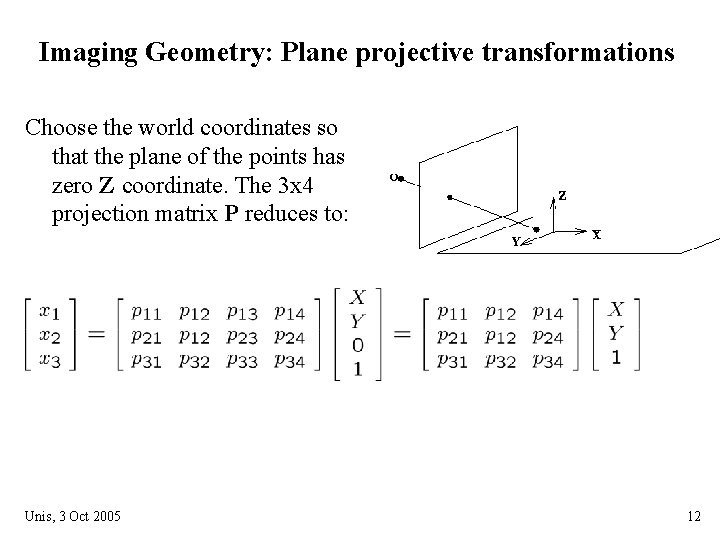
Imaging Geometry: Plane projective transformations Choose the world coordinates so that the plane of the points has zero Z coordinate. The 3 x 4 projection matrix P reduces to: Unis, 3 Oct 2005 12

Image Geometry: Computing Plane Projective Transform 1 • The plane projective transform is called a homography • Four point-to-point correspondences define a homography • From the model of pinhole camera, we know the form (» denotes similarity up to scale): or, equivalently: Unis, 3 Oct 2005 13

Image Geometry: Computing Plane Projective Transform 2 • Each point correspondence defines two constraints: • Multiplying out: • Two approaches can be used to address the scale ambiguity. We will use the simpler one that sets h 33=1. This is OK unless points at infinity are involved Unis, 3 Oct 2005 14

Image Geometry: Computing Plane Projective Transform 3 • The constrains from four points can be expressed as a linear (in unknowns hij) into an 8 x 8 matrix: Unis, 3 Oct 2005 15

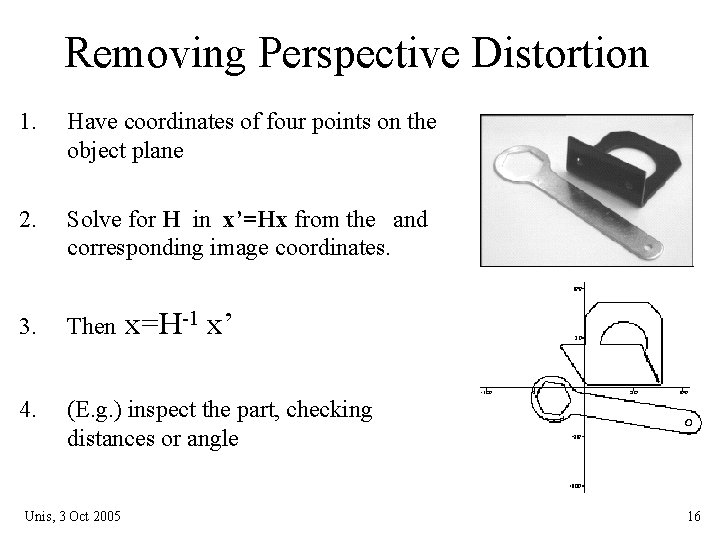
Removing Perspective Distortion 1. Have coordinates of four points on the object plane 2. Solve for H in x’=Hx from the and corresponding image coordinates. 3. Then 4. (E. g. ) inspect the part, checking distances or angle Unis, 3 Oct 2005 x=H-1 x’ 16

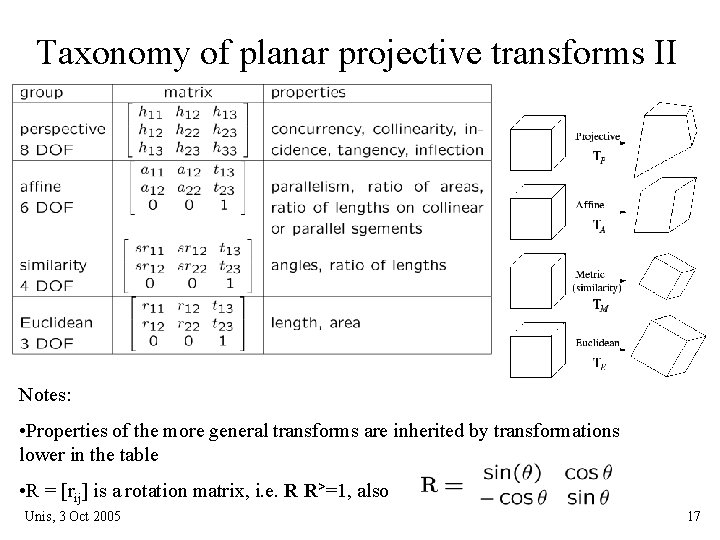
Taxonomy of planar projective transforms II Notes: • Properties of the more general transforms are inherited by transformations lower in the table • R = [rij] is a rotation matrix, i. e. R R>=1, also Unis, 3 Oct 2005 17

Taxonomy of planar projective transforms I • In many circumstances, we know from the imaging setup, that the image-to-image transformation is simpler than homography or can be well approximated by a transformation with a lower number of degrees of freedom. • Three types of transforms are commonly encountered: – Euclidean (shifted and rotated, e. g. two flatbed scans of the same image ) – Similarity (shift, rotation, isotropic scaling, e. g. two photos from the same spot with different zoom) – Affine transformation Unis, 3 Oct 2005 18

Image Geometry: Computing Affine Transform • An affine transform is defined as: • Each point-to-point correspondence provides to constraints, correspondences are needed to uniquely define the transformation. 3 • Solving the problem requires inversion of a single 3 x 3 matrix: Unis, 3 Oct 2005 19

Unis, 3 Oct 2005 20