Images photometric aspects of image formation gray level








![Discrete time system • Maps 1 discrete time signal to another f[x] h g[x] Discrete time system • Maps 1 discrete time signal to another f[x] h g[x]](https://slidetodoc.com/presentation_image_h/bfcfded75a306829279e245672a6a88f/image-10.jpg)

















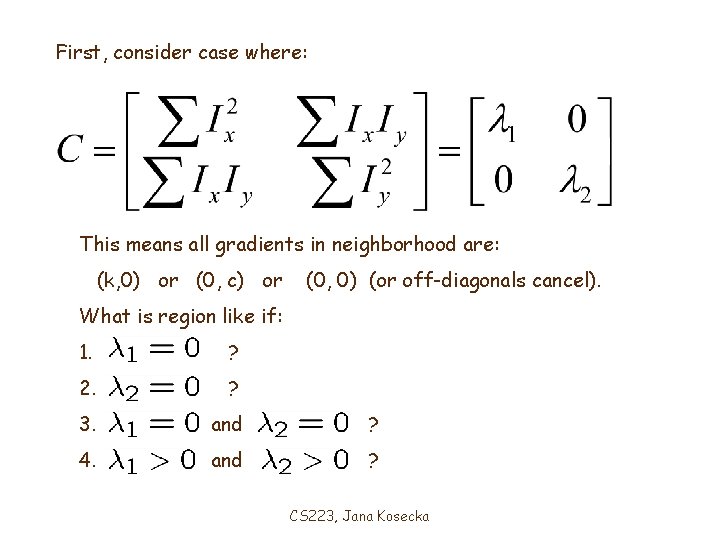



















- Slides: 64

Images - photometric aspects of image formation - gray level images - linear/nonlinear filtering - edge detection - corner detection CS 223, Jana Kosecka

Image Brightness values I(x, y) CS 223, Jana Kosecka

Image model Mathematical tools Analog intensity function Analysis Temporal/spatial sampled function Linear algebra Quantization of the gray levels Numerical methods Point sets Set theory, morphology Random fields Stochastic methods List of image features, regions Geometry, AI, logic CS 223, Jana Kosecka

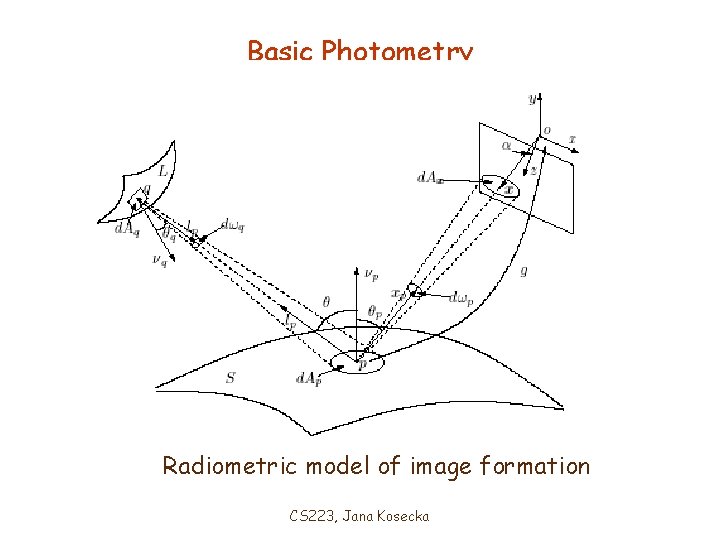
Basic Photometry Radiometric model of image formation CS 223, Jana Kosecka

Basic ingredients Radiance – amount of energy emitted along certain direction Iradiance – amount of energy received along certain direction BRDF – bidirectional reflectance distribution – portion of the energy coming from direction reflected to direction Lambertian surfaces – the appearance depends only on radiance, not on the viewing direction Image intensity for a Lambertian surface CS 223, Jana Kosecka

Images • Images contain noise – sources sensor quality, light fluctuations, quantization effects CS 223, Jana Kosecka

Image Noise Models • Additive noise: most commonly used • Multiplicative noise: • Impulsive noise (salt and pepper): • Noise models: gaussian, uniform • Noise Amount: SNR = s/ n CS 223, Jana Kosecka

Image filtering • How can we reduce the noise in the image • Image acquisition noise due to light fluctuations and sensor noise can be reduced by acquiring a sequence of images and averaging them • Computation of simple features • First stage of visual processing CS 223, Jana Kosecka

Image Processing 1 D signal and its sampled version f = { f(1), f(2), f(3), …, f(n)} f = {0, 1, 2, 3, 4, 5, 5, 6, 10 } CS 223, Jana Kosecka
![Discrete time system Maps 1 discrete time signal to another fx h gx Discrete time system • Maps 1 discrete time signal to another f[x] h g[x]](https://slidetodoc.com/presentation_image_h/bfcfded75a306829279e245672a6a88f/image-10.jpg)
Discrete time system • Maps 1 discrete time signal to another f[x] h g[x] • Special class of systems – linear , time-invariant systems Superposition principle Shift (time) invariant – shift in input causes shift in output CS 223, Jana Kosecka

Convolution sum: unit impluse – if x = 0 it’s 1 and zero everywhere else Every discrete time signal can be written as a sum of scaled and shifted impulses The output the linear system is related to the input and the transfer function via convolution f h g f Convolution sum: Notation: CS 223, Jana Kosecka filter g

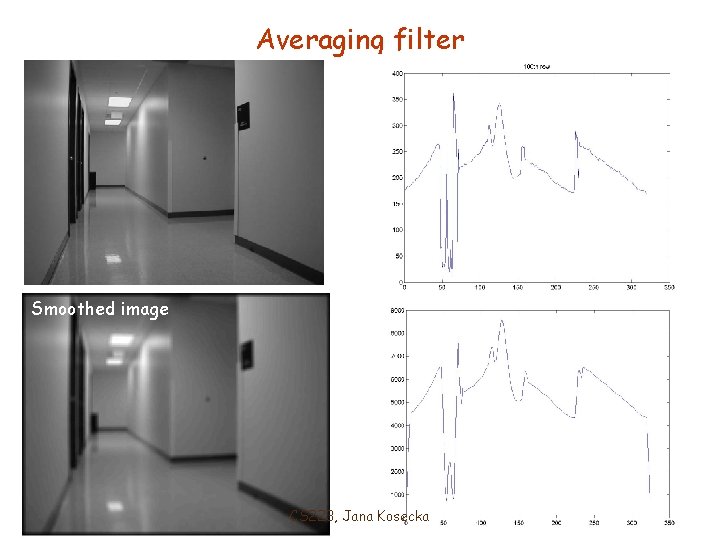
Averaging filter Original image Smoothed image CS 223, Jana Kosecka

Averaging filter and 0 everywhere else Box filter Ex. cont. Averaging filter center pixel weighted more CS 223, Jana Kosecka

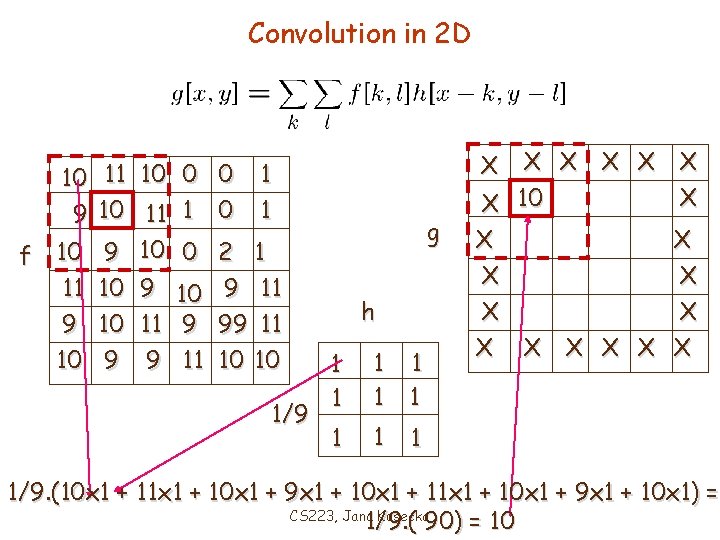
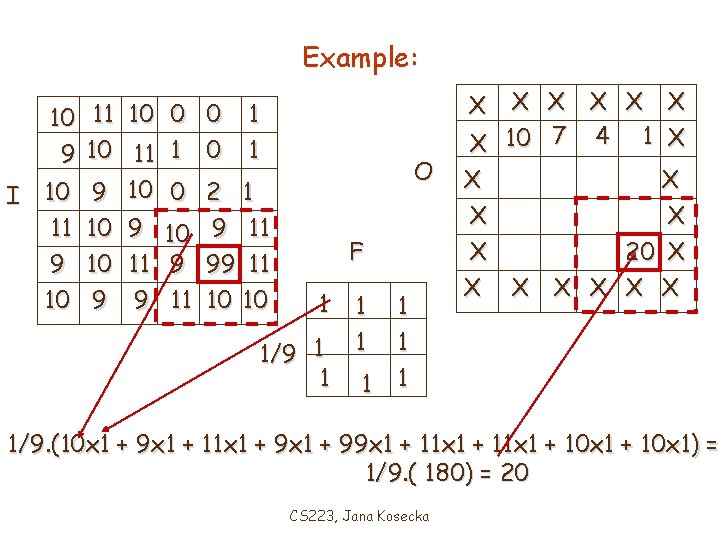
Convolution in 2 D 10 11 10 0 0 1 9 10 11 1 0 1 f 10 9 10 0 2 1 11 10 9 11 9 10 11 9 99 11 10 9 9 11 10 10 1/9 X X X X 10 X X X X g h 1 1 1 1 1/9. (10 x 1 + 11 x 1 + 10 x 1 + 9 x 1 + 10 x 1) = CS 223, Jana Kosecka 1/9. ( 90) = 10

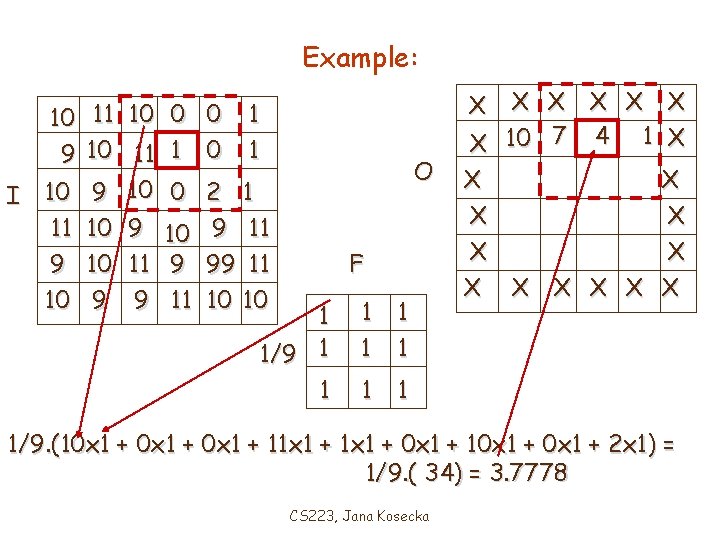
Example: 10 11 10 0 0 1 9 10 11 1 0 1 I 10 9 10 0 2 1 11 10 9 11 9 10 11 9 99 11 10 9 9 11 10 10 X X X 10 7 4 1 X X X X O F 1 1/9 1 1 1 1 1/9. (10 x 1 + 11 x 1 + 0 x 1 + 10 x 1 + 2 x 1) = 1/9. ( 34) = 3. 7778 CS 223, Jana Kosecka

Example: 10 11 10 0 0 1 9 10 11 1 0 1 I 10 9 10 0 2 1 11 10 9 11 9 10 11 9 99 11 10 9 9 11 10 10 X X X 10 7 4 1 X X X 20 X X X X O F 1 1/9 1 1 1 1 1/9. (10 x 1 + 9 x 1 + 11 x 1 + 99 x 1 + 11 x 1 + 10 x 1) = 1/9. ( 180) = 20 CS 223, Jana Kosecka

How big should the mask be? • The bigger the mask, – more neighbors contribute – bigger noise spread. – more blurring. – more expensive to compute Limitations of averaging • Signal frequencies shared with noise are lost • Impulsive noise is diffused but not removed CS 223, Jana Kosecka

Gaussian Filter • Better option for blurring – The coefficients are samples of a 1 D Gaussian. – Gives more weight at the central pixel and less weights to the neighbors. – The further away the neighbors, the smaller the weight. – Gaussian filter Samples from the continuous Gaussian • Gaussian filter is the only one that has the same shape in the space and frequency domains. • There are no secondary lobes – i. e. a truly low-pass filter CS 223, Jana Kosecka

How big should the mask be? • The std. dev of the Gaussian determines the amount of smoothing. • The samples should adequately represent a Gaussian • For a 98. 76% of the area, we need m = 5 5. (1/ ) 2 0. 796, m 5 5 -tap filter g[x] = [0. 136, 0. 6065, 1. 00, 0. 606, 0. 136] CS 223, Jana Kosecka

Image Smoothing • Convolution with a 2 D Gaussian filter • Gaussian filter is separable, convolution can be accomplished as two 1 -D convolutions CS 223, Jana Kosecka

Non-linear Filtering • Replace each pixel with the MEDIAN value of all the pixels in the neighborhood • Non-linear • Does not spread the noise • Can remove spike noise • Expensive to run CS 223, Jana Kosecka

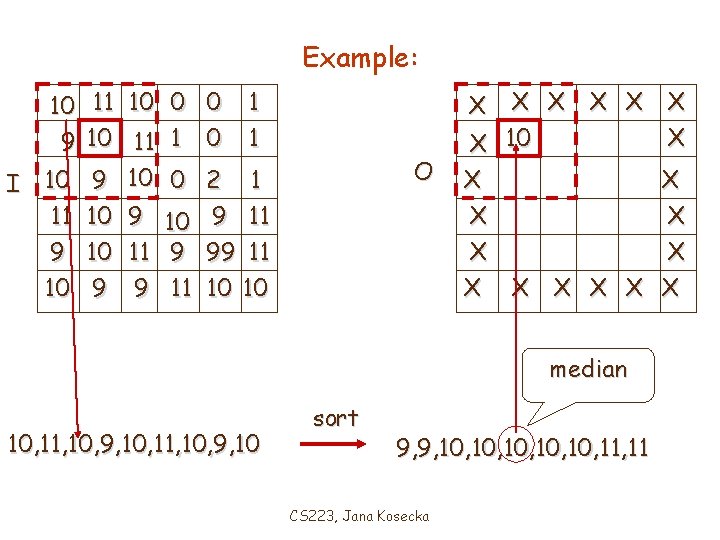
Example: 10 11 10 0 0 1 9 10 11 1 0 1 I 10 9 10 0 2 1 11 10 9 11 9 10 11 9 99 11 10 9 9 11 10 10 X X X X O median 10, 11, 10, 9, 10 sort 9, 9, 10, 10, 10, 11 CS 223, Jana Kosecka X X X

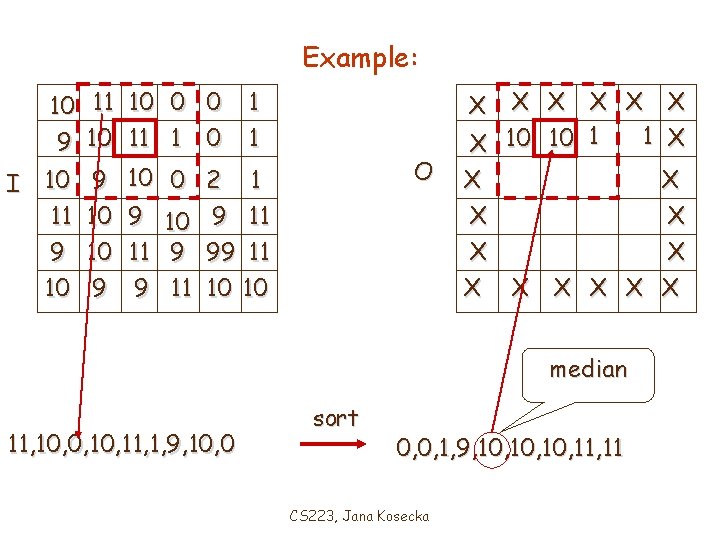
Example: 10 11 10 0 0 9 10 11 1 0 I 10 11 9 10 1 1 X X X 10 10 1 X X X X O 9 10 0 2 1 10 9 11 10 11 9 99 11 9 9 11 10 10 median 11, 10, 0, 11, 1, 9, 10, 0 sort 0, 0, 1, 9, 10, 10, 11 CS 223, Jana Kosecka

Example: I 10 11 10 0 0 1 9 10 11 1 0 1 10 9 10 0 2 1 11 10 9 11 9 10 11 9 99 11 10 9 9 11 10 10 X X X X 10 X X 9 X X X 10 X X X X O median 10, 9, 11, 9, 99, 11, 10 sort 9, 9, 10, 10, 11, 11, 99 CS 223, Jana Kosecka

Image Features Local, meaningful, detectable parts of the image. We will look at edges and corners CS 223, Jana Kosecka

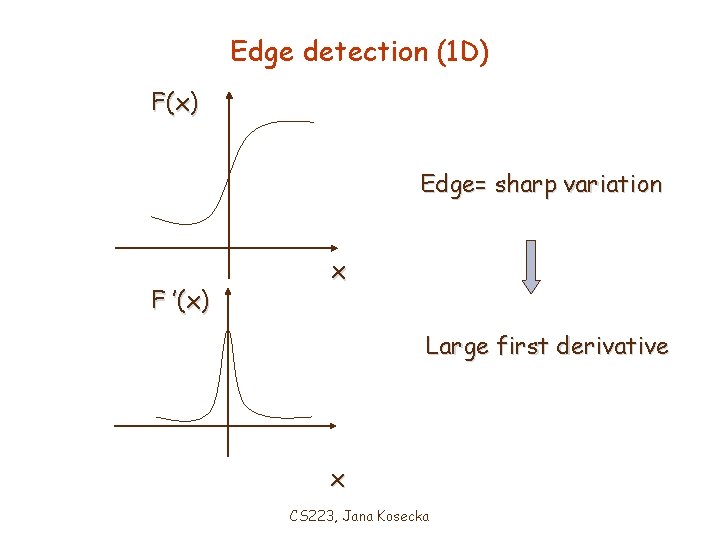
Image Features – Edges, Corners • Look for detectable, meaningful parts of the image • Edges are detected at places where the image values exhibit sharp variation Gray value column Edge CS 223, Jana Kosecka

Edge detection (1 D) F(x) Edge= sharp variation F ’(x) x Large first derivative x CS 223, Jana Kosecka

Digital Approximation of 1 st derivatives f(x) X-1 Convolve with: -1 0 CS 223, Jana Kosecka 1 X X+1

Edge Detection (2 D) Vertical Edges: Convolve with: Horizontal Edges: Convolve with: -1 0 1 CS 223, Jana Kosecka 1

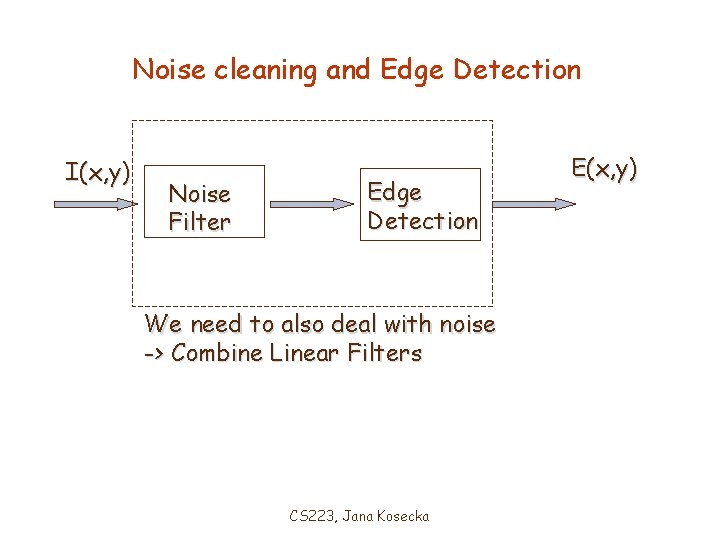
Noise cleaning and Edge Detection I(x, y) Noise Filter Edge Detection We need to also deal with noise -> Combine Linear Filters CS 223, Jana Kosecka E(x, y)

Convolve with: -1 0 1 Noise Smoothing & Edge Detection Vertical Edge Detection This mask is called the (vertical) Prewitt Edge Detector Outer product of box filter [1 1 1]T and [-1 0 1] CS 223, Jana Kosecka

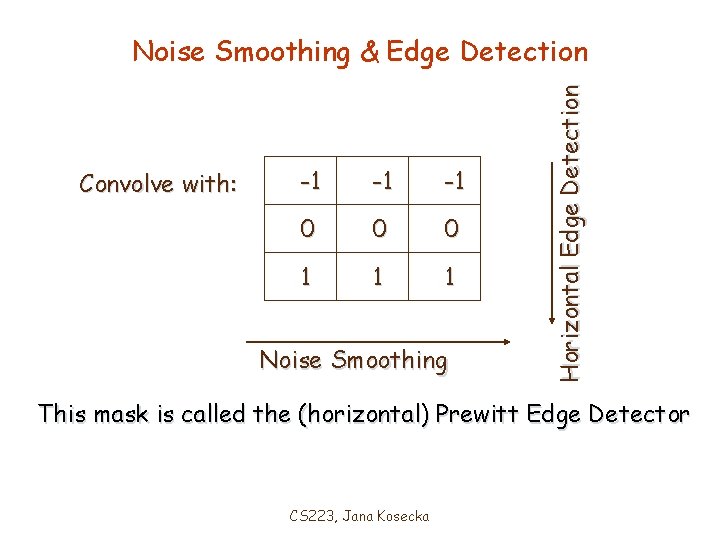
Convolve with: -1 -1 -1 0 0 0 1 1 1 Noise Smoothing Horizontal Edge Detection Noise Smoothing & Edge Detection This mask is called the (horizontal) Prewitt Edge Detector CS 223, Jana Kosecka

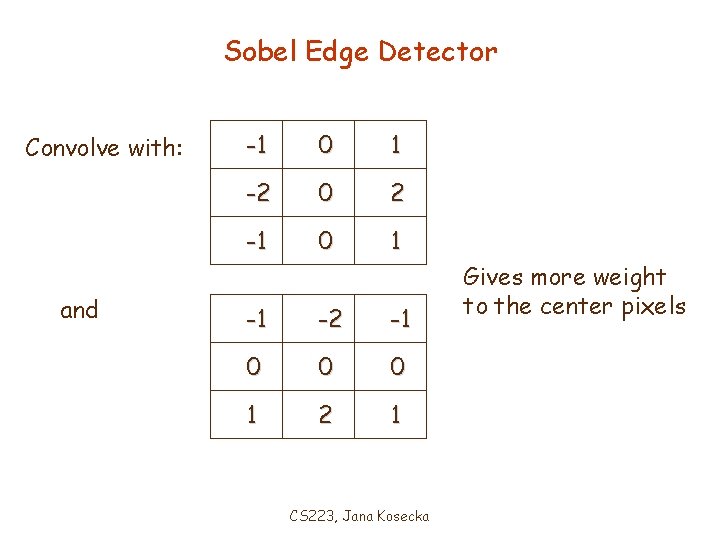
Sobel Edge Detector Convolve with: and -1 0 1 -2 0 2 -1 0 1 -1 -2 -1 0 0 0 1 2 1 CS 223, Jana Kosecka Gives more weight to the center pixels

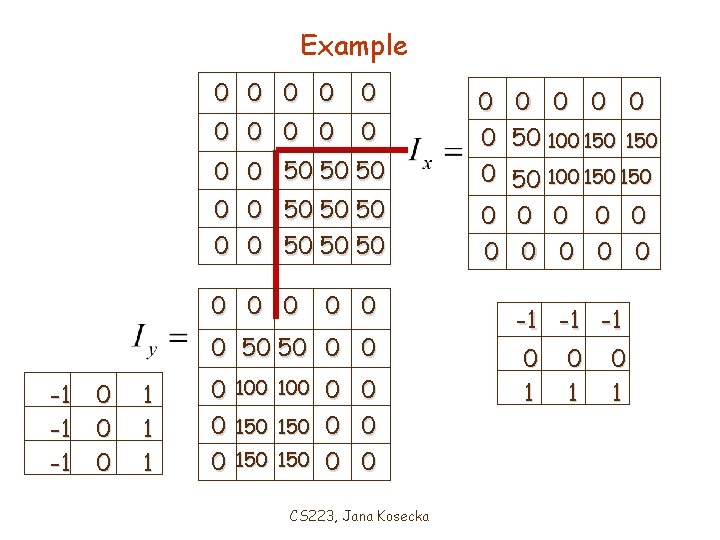
Example 0 0 0 50 50 50 0 0 0 50 50 0 0 -1 -1 -1 0 0 0 1 1 1 0 100 0 0 0 150 150 0 0 CS 223, Jana Kosecka 0 0 0 50 100 150 150 0 0 0 -1 -1 -1 0 1 0 1

Image Derivatives We know better alternative to smoothing Smooth using Gaussian filter g(x) is a 1 -D Gaussian filter, g(x, y) – 2 -D Gaussian filter Taking a derivative – linear operation (take the derivative of the filter) CS 223, Jana Kosecka

Gaussian and its derivative CS 223, Jana Kosecka

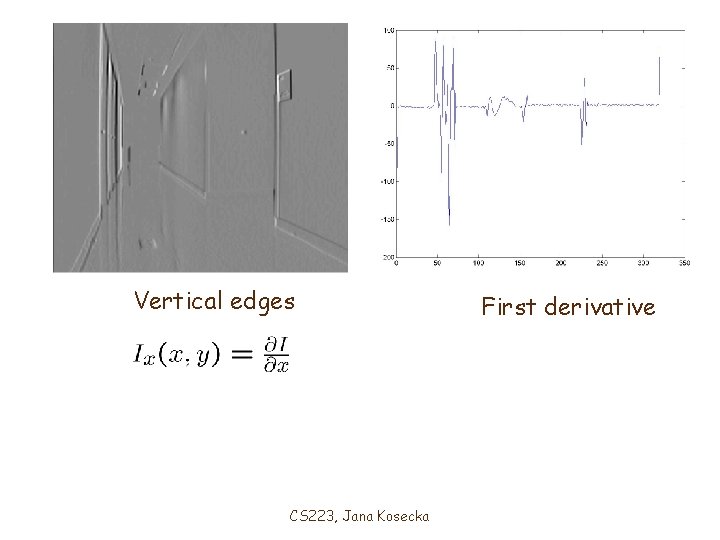
Vertical edges CS 223, Jana Kosecka First derivative

Gradient Magnitude Horizontal edges • Image Gradient CS 223, Jana Kosecka

Gradient Orientation CS 223, Jana Kosecka

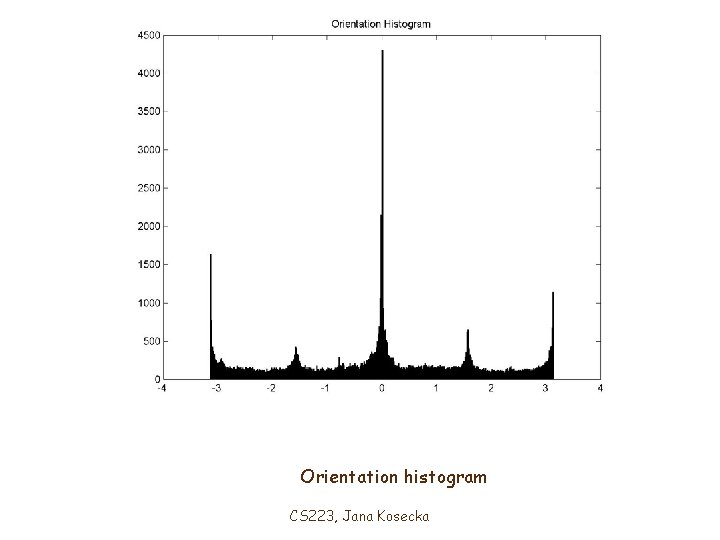
Orientation histogram CS 223, Jana Kosecka

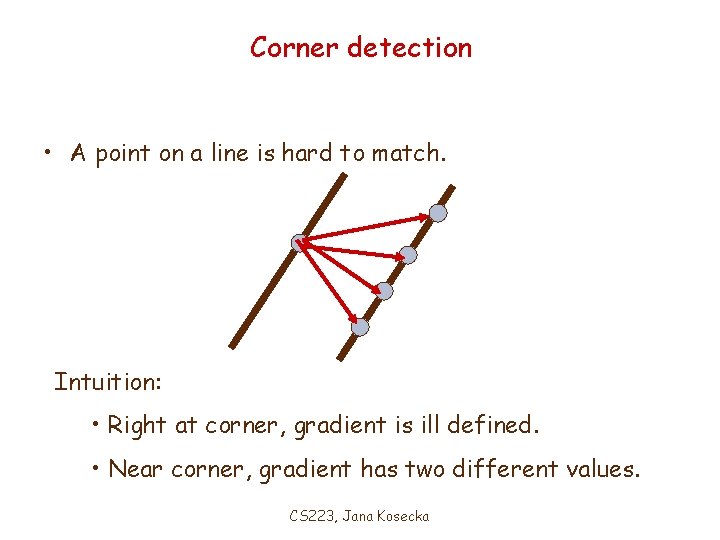
Corner detection • A point on a line is hard to match. Intuition: • Right at corner, gradient is ill defined. • Near corner, gradient has two different values. CS 223, Jana Kosecka

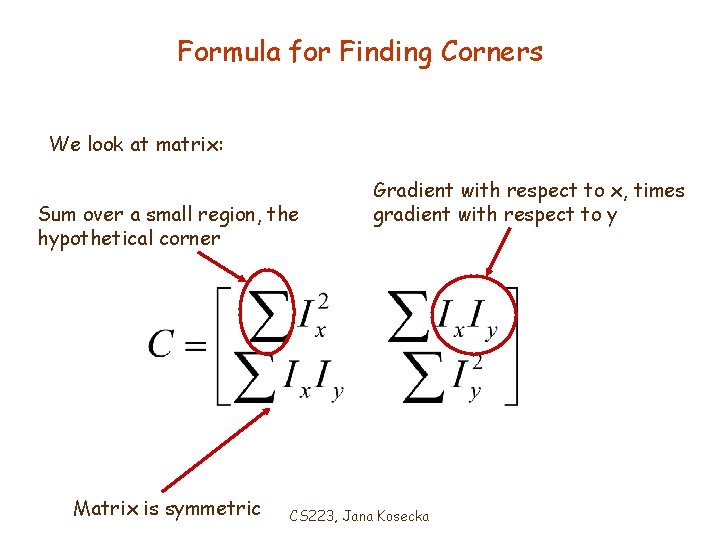
Formula for Finding Corners We look at matrix: Sum over a small region, the hypothetical corner Matrix is symmetric Gradient with respect to x, times gradient with respect to y CS 223, Jana Kosecka
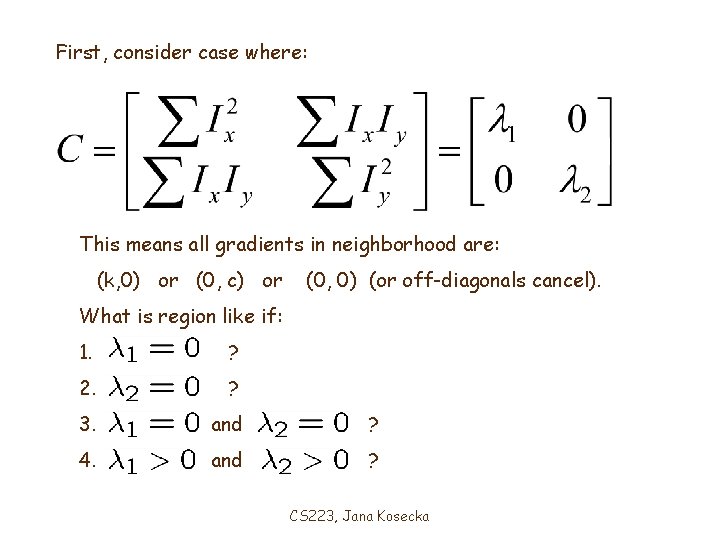
First, consider case where: This means all gradients in neighborhood are: (k, 0) or (0, c) or (0, 0) (or off-diagonals cancel). What is region like if: 1. ? 2. ? 3. and ? 4. and ? CS 223, Jana Kosecka

General Case: In general case from linear algebra, it follows that because C is symmetric: With R being a rotation matrix. So every case can be intrepreted like on last slide. CS 223, Jana Kosecka

Corner Detection • • • Filter image. Compute magnitude of the gradient everywhere. We construct C in a window. Compute eigenvalues l 1 and l 2. If they are both big, we have a corner Or if smalest eigenvalue of C is bigger than - mark pixel as candidate feature point CS 223, Jana Kosecka

Point Feature Extraction Harris Corner Detector • Alternatively feature quality function (Harris Corner Detector) CS 223, Jana Kosecka

Harris Corner Detector - Example CS 223, Jana Kosecka

Edge Detection gradient magnitude original image • Compute image derivatives • if gradient magnitude > and the value is a local max. along gradient direction – pixel is an edge candidate • how to detect one pixel thin edges ? CS 223, Jana Kosecka

Canny Edge Detector • The magnitude image Es has the magnitudes of the smoothed gradient. • Sigma determines the amount of smoothing. • Es has large values at edges: – Find local maxima Th CS 223, Jana Kosecka

Nonmaximum supression • • The inputs are Es & Eo Magnitude and orientation Consider 4 directions D={ 0, 45, 90, 135} wrt x • For each pixel (i, j) do: 1. 2. • Find the direction d D s. t. d Eo(i, j) (normal to the edge) If {Es(i, j) is smaller than at least one of its neigh. along d} • IN(i, j)=0 • Otherwise, IN(i, j)= Es(i, j) The output is the thinned edge image IN x CS 223, Jana Kosecka x

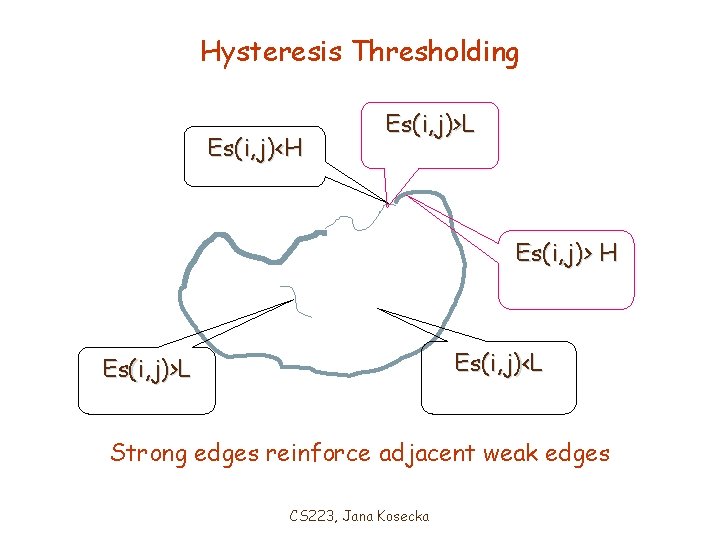
Thresholding • Edges are found by thresholding the output of NONMAX_SUPRESSION • If the threshold is too high: – Very few (none) edges • High MISDETECTIONS, many gaps • If the threshold is too low: – Too many (all pixels) edges • High FALSE POSITIVES, many extra edges CS 223, Jana Kosecka

Hysteresis Thresholding Es(i, j)<H Es(i, j)>L Es(i, j)> H Es(i, j)<L Es(i, j)>L Strong edges reinforce adjacent weak edges CS 223, Jana Kosecka

Finding lines in an image • Option 1: – Search for the line at every possible position/orientation – What is the cost of this operation? • Option 2: – Use a voting scheme: Hough transform CS 223, Jana Kosecka

Other edge detectors - second-order derivative filters (1 D) • Peaks of the first-derivative of the input signal, correspond to “zero-crossings” of the secondderivative of the input signal. F(x) F’’(x) F ’(x) x CS 223, Jana Kosecka

Edge Detection (2 D) y 1 D F(x) I(x) dx d 2 I(x) dx 2 2 D x > Th =0 x I(x, y) | I(x, y)| =(Ix 2(x, y) + Iy 2(x, y))1/2 > Th tan = Ix(x, y)/ Iy(x, y) 2 I(x, y) =Ix x (x, y) + Iyy (x, y)=0 Laplacian CS 223, Jana Kosecka

Notes about the Laplacian: • • 2 I(x, y) is a SCALAR – Can be found using a SINGLE mask – Orientation information is lost 2 I(x, y) is the sum of SECOND-order derivatives – But taking derivatives increases noise – Very noise sensitive! It is always combined with a smoothing operation: Filter Laplacian of Gaussian LOG filter I(x, y) Smooth Laplacian CS 223, Jana Kosecka O(x, y)

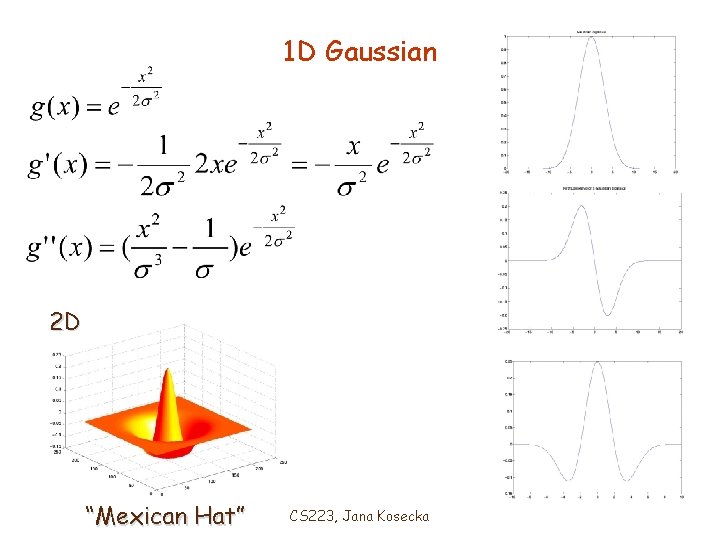
1 D Gaussian 2 D “Mexican Hat” CS 223, Jana Kosecka

Derivative of Gaussian Filters Measure the image gradient and its direction at different scales (use a pyramid). CS 223, Jana Kosecka

The Laplacian Pyramid • Building a Laplacian pyramid: – Create a Gaussian pyramid – Take the difference between one Gaussian pyramid level and the next (before subsampling) • Properties – Also known as the difference-of-Gaussian function, which is a close approximation to the Laplacian – It is a band pass filter - each level represents a different band of spatial frequencies • Reconstructing the original image: – Reconstruct the Gaussian pyramid starting at top layer CS 223, Jana Kosecka

CS 223, Jana Kosecka Gaussian pyramid

Laplacian Pyramid (note top image is from Gaussian) CS 223, Jana Kosecka

Add more oriented filters (Malik & Perona, 1990) CS 223, Jana Kosecka

Alternative: Gabor filters: Product of a Gaussian with sine or cosine Top row shows anti-symmetric (or odd) filters, bottom row the symmetric (or even) filters. No obvious advantage to any one type of oriented filters. CS 223, Jana Kosecka

An edge is not a line. . . • How can we detect lines ? CS 223, Jana Kosecka