Image Transforms Transforming images to images Image Processing

Image Transforms Transforming images to images Image Processing and Computer Vision: 2

Classification of Image Transforms n Point transforms n n n Local transforms n n modify individual pixels modify pixels’ locations output derived from neighbourhood Global transforms n whole image contributes to each output value Image Processing and Computer Vision: 2 2

Point Transforms n Manipulating individual pixel values n n n Histogram manipulation n n Brightness adjustment Contrast adjustment equalisation Image magnification Image Processing and Computer Vision: 2 3

Grey Scale Manipulation n Brightness modifications Contrast modifications Histogram manipulation Image Processing and Computer Vision: 2 4

Brightness Adjustment Add a constant to all values g’ = g + k (k = 50) Image Processing and Computer Vision: 2 5

Contrast Adjustment Scale all values by a constant g’ = g*k (k = 1. 5) Image Processing and Computer Vision: 2 6

Image Histogram n Measure frequency of occurrence of each grey/colour value Image Processing and Computer Vision: 2 7

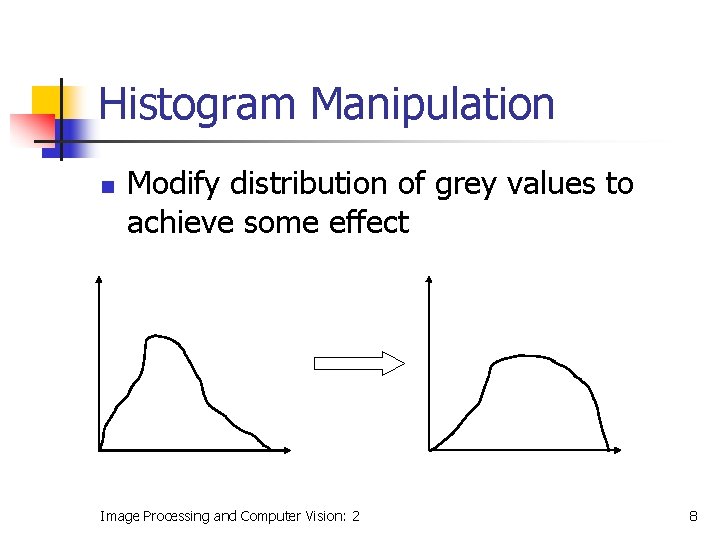
Histogram Manipulation n Modify distribution of grey values to achieve some effect Image Processing and Computer Vision: 2 8

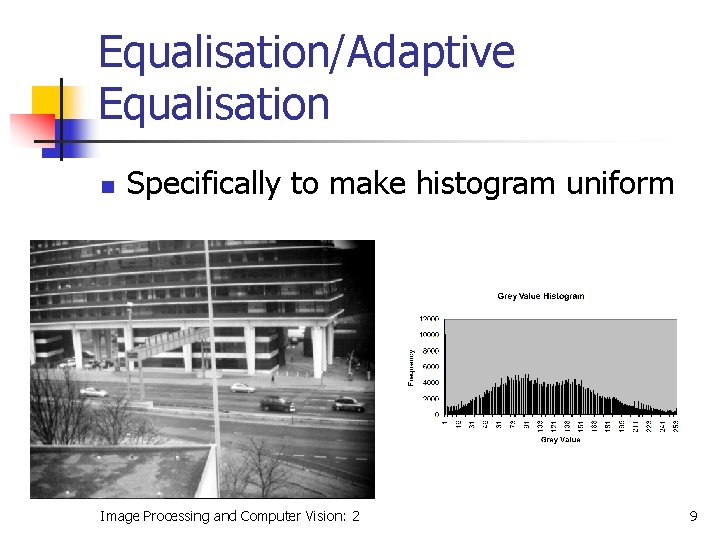
Equalisation/Adaptive Equalisation n Specifically to make histogram uniform Image Processing and Computer Vision: 2 9

Equalisation Transform n n Equalised image has n x m/l pixels per grey level Cumulative to level j n n jnm/l pixels Equate to a value in input cumulative histogram C[i] n n n C[i] = jnm/l j = C[i]l/nm Modifications to prevent mapping to – 1. Image Processing and Computer Vision: 2 10

Thresholding n n Transform grey/colour image to binary if f(x, y) > T output = 1 else 0 How to find T? Image Processing and Computer Vision: 2 11

Threshold Value n Manual n n User defines a threshold P-Tile Mode Other automatic methods Image Processing and Computer Vision: 2 12

P-Tile n n If we know the proportion of the image that is object Threshold the image to select this proportion of pixels Image Processing and Computer Vision: 2 13

Mode Threshold at the minimum between the histogram’s peaks. Image Processing and Computer Vision: 2 14

Automated Methods Find a threshold such that Average l Average h (Start at = 0 and work upwards. ) Image Processing and Computer Vision: 2 15

Image Magnification n Reducing n new value is weighted sum of nearest neighbours new value equals nearest neighbour Enlarging n n new value is weighted sum of nearest neighbours add noise to obscure pixelation Image Processing and Computer Vision: 2 16

Local Transforms n n Convolution Applications n n n smoothing sharpening matching Image Processing and Computer Vision: 2 17

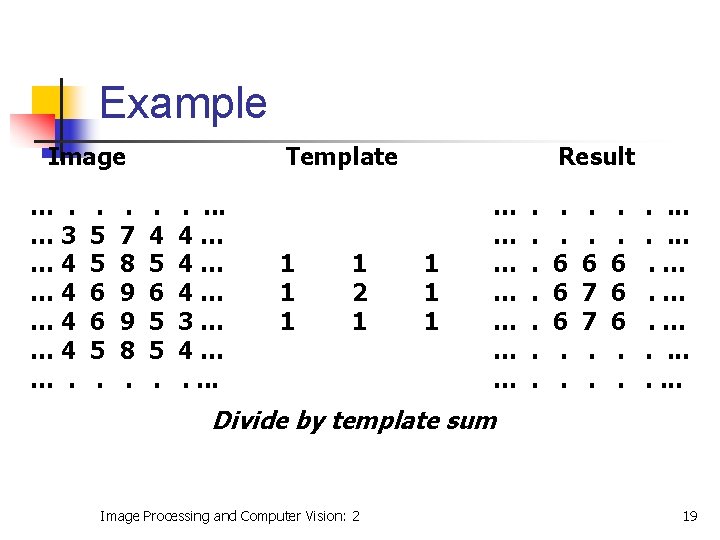
Convolution Definition Place template on image Multiply overlapping values in image and template Sum products and normalise (Templates usually small) Image Processing and Computer Vision: 2 18

Example Image …. … 3 … 4 … 4 …. . 5 5 6 6 5. . 7 8 9 9 8. Template. 4 5 6 5 5. . . 4… 4… 4… 3… 4…. . 1 1 2 1 Result 1 1 1 … … … … . . 6 6 6. . 6 7 7. . 6 6 6. . . …. …. …. . . . Divide by template sum Image Processing and Computer Vision: 2 19

Separable Templates n Convolve with n x n template n n n 2 multiplications and additions Convolve with two n x 1 templates n 2 n multiplications and additions Image Processing and Computer Vision: 2 20

Example n Laplacian template n Separated kernels -1 2 -1 Image Processing and Computer Vision: 2 0 – 1 0 -1 4 – 1 0 -1 21

Composite Filters n n Convolution is distributive Can create a composite filter and do a single convolution Not convolve image with one filter and convolve result with second. Efficiency gain Image Processing and Computer Vision: 2 22

Applications n Usefulness of convolution is the effects generated by changing templates n Smoothing n n Sharpening n n Noise reduction Edge enhancement Template matching n A later lecture Image Processing and Computer Vision: 2 23

Smoothing n n n Aim is to reduce noise What is “noise”? How is it reduced n n n Addition Adaptively Weighted Image Processing and Computer Vision: 2 24

Noise Definition n Noise is deviation of a value from its expected value n Random changes n n x x+n Salt and pepper n x {max, min} Image Processing and Computer Vision: 2 25

Noise Reduction n By smoothing S(x + n) = S(x) + S(n) = S(x) n n n Since noise is random and zero mean Smooth locally or temporally Local smoothing n n Removes detail Introduces ringing Image Processing and Computer Vision: 2 26

Adaptive Smoothing n Compute smoothed value, s Output = s if |s – x| > T x otherwise Image Processing and Computer Vision: 2 27

Median Smoothing Median is one value in an ordered set: 1 2 3 4 5 6 7 median = 4. 5 Image Processing and Computer Vision: 2 28

Original Smoothed Median Smoothing Image Processing and Computer Vision: 2 29

Gaussian Smoothing n n n To reduce ringing Weighted smoothing Numbers from Gaussian (normal) distribution are weights. Image Processing and Computer Vision: 2 30

Sharpening n What is it? n n n Enhancing discontinuities Edge detection Why do it? n n Perceptually important Computationally important Image Processing and Computer Vision: 2 31

Edge Definition An edge is a significant local change in image intensity. Image Processing and Computer Vision: 2 32

Edge Types n Step edge Line edge Roof edge n Real edges n n Image Processing and Computer Vision: 2 33

First Derivative, Gradient Edge Detection n n If an edge is a discontinuity Can detect it by differencing Image Processing and Computer Vision: 2 34

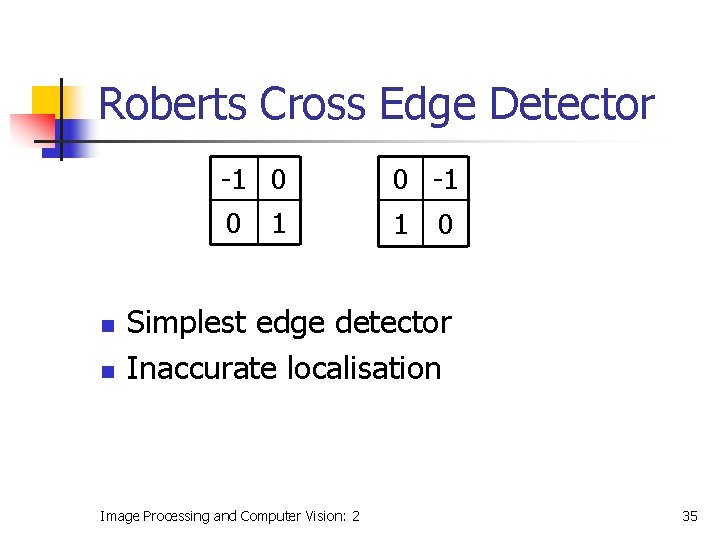
Roberts Cross Edge Detector n n -1 0 0 -1 0 1 1 0 Simplest edge detector Inaccurate localisation Image Processing and Computer Vision: 2 35

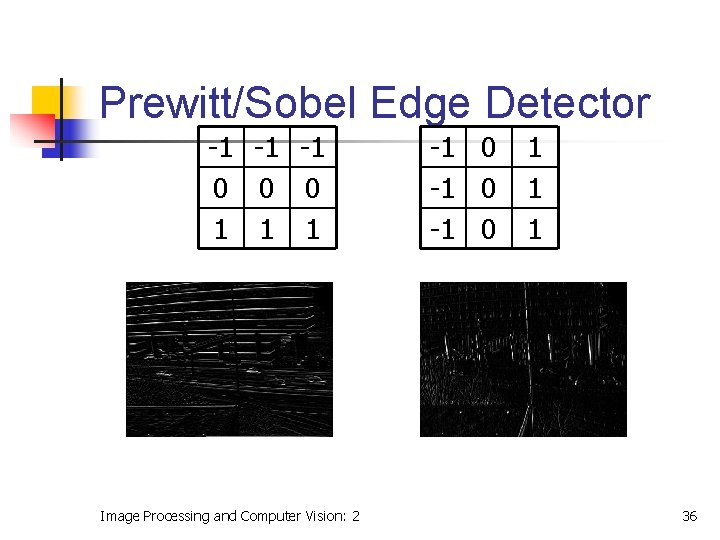
Prewitt/Sobel Edge Detector -1 -1 -1 0 0 0 1 1 1 Image Processing and Computer Vision: 2 -1 0 1 1 1 36

Edge Detection n Combine horizontal and vertical edge estimates Image Processing and Computer Vision: 2 37

Problems n n Enhanced edges are noise sensitive Scale n What is “local”? Image Processing and Computer Vision: 2 38

Canny/Deriche Edge Detector n Require n n edges to be detected accurate localisation single response to an edge Solution n Convolve image with Difference of Gaussian (Do. G) Image Processing and Computer Vision: 2 39

Example Results Image Processing and Computer Vision: 2 40

Second Derivative Operators Zero Crossing n n Model HVS Locate edge to subpixel accuracy Convolve image with Laplacian of Gaussian (Lo. G) Edge location at crossing of zero axis Image Processing and Computer Vision: 2 41

Example Results Image Processing and Computer Vision: 2 42

Image Processing and Computer Vision: 2 43

Global Transforms n n n Computing a new value for a pixel using the whole image as input Cosine and Sine transforms Fourier transform n n Frequency domain processing Hough transform Karhunen-Loeve transform Wavelet transform Image Processing and Computer Vision: 2 44

Cosine/Sine n n A halfway solution to the Fourier Transform Used in image coding Image Processing and Computer Vision: 2 45

Fourier n All periodic signals can be represented by a sum of appropriately weighted sine/cosine waves Image Processing and Computer Vision: 2 46

Transformed section of BT Building image. Image Processing and Computer Vision: 2 47

Frequency Domain Filtering n Convolution Theorem: Convolution in spatial domain is equivalent to Multiplication in frequency domain Image Processing and Computer Vision: 2 48

Smoothing Suppress high frequency components Image Processing and Computer Vision: 2 49

Sharpening Suppress low frequency components Image Processing and Computer Vision: 2 50

Example Image Processing and Computer Vision: 2 51

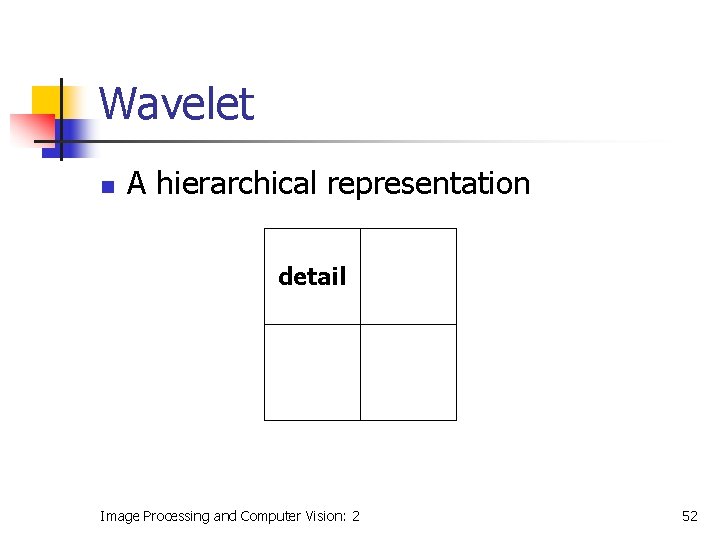
Wavelet n A hierarchical representation detail Image Processing and Computer Vision: 2 52

Hough Transform n n To detect curves analytically Example n straight lines Image Processing and Computer Vision: 2 53

Straight Line y = mx + c gradient m, intercept c c = -mx + y gradient -x, intercept y ALL points in (x, y) transform to a straight line in (c, m) Can therefore detect collinear points Image Processing and Computer Vision: 2 54

Analytic Curve Finding n Alternative representation n n to avoid infinities Other curves n higher dimensional accumulators Image Processing and Computer Vision: 2 55

Performance Improvement Techniques n n Look at pairs of points Use edge orientation Image Processing and Computer Vision: 2 56

Karhunen-Loeve (Principal Component) n n A compact method of representing variation in a set of images PCs define a co-ordinate system n n n 1 st PC records most of variation 2 nd PC records most of remainder etc Image Processing and Computer Vision: 2 57

Method n n n Take a set of typical images Compute mean image and subtract from each sample Transform images into columns Group images into a matrix Compute covariance matrix Compute eigenvectors n n these are the PCs eigenvalues show their importance Image Processing and Computer Vision: 2 58

Uses n n Compact representation of variable data Object recognition Image Processing and Computer Vision: 2 59

Uses n n n Hierarchical representation Multiresolution processing Coding Image Processing and Computer Vision: 2 60

Geometric Transformations n Definitions n n Affine and non-affine transforms Applications n Manipulating image shapes Image Processing and Computer Vision: 2 61

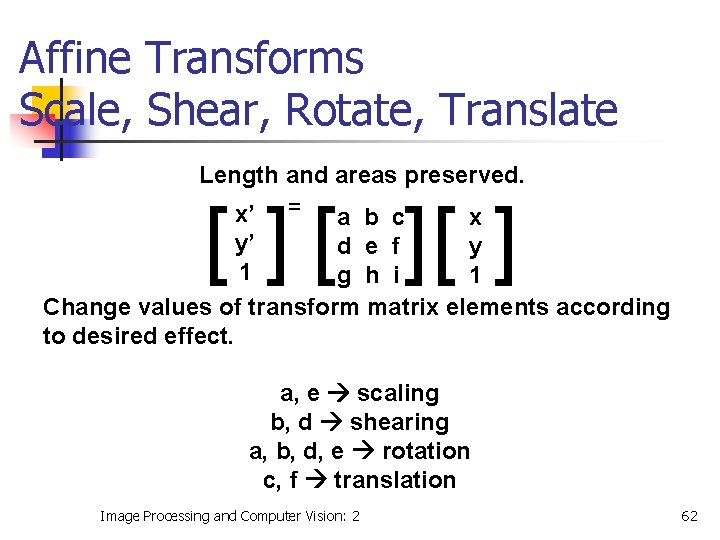
Affine Transforms Scale, Shear, Rotate, Translate Length and areas preserved. x’ = a b c x y’ d e f y 1 g h i 1 Change values of transform matrix elements according to desired effect. [ ][ ] a, e scaling b, d shearing a, b, d, e rotation c, f translation Image Processing and Computer Vision: 2 62

Affine Transform Examples Image Processing and Computer Vision: 2 63

Warping Example Ansell Adams’ Aspens Image Processing and Computer Vision: 2 64

Image Resampling n n n Moving source to destination pixels x’ and y’ could be non-integer Round result n n can create holes in image Manipulate in reverse n n where did warped pixel come from source is non-integer n interpolate nearest neighbours Image Processing and Computer Vision: 2 65

You Should Know… n Point transforms n n Local transforms n n edge detection, smoothing Global transforms n n scaling, histogram manipulation, thresholding Fourier, Hough, Principal Component, Wavelet Geometrical transforms Image Processing and Computer Vision: 2 66