Image Synthesis Rabie A Ramadan Ph D 7

Image Synthesis Rabie A. Ramadan, Ph. D 7

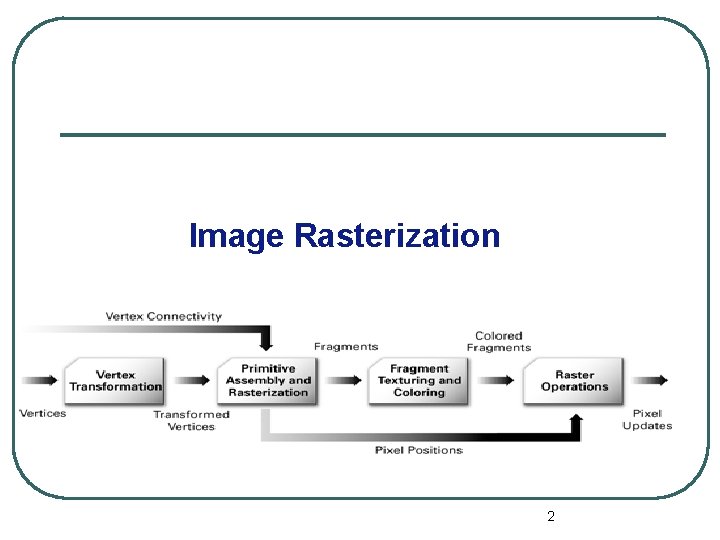
Image Rasterization 2

Rasterization and Fragment Processing l A precise sequence of steps for converting primitives into patterns of pixel values in the framebuffer. l Digital images created or captured (for example, by scanning in a photo) as a set of samples of a given space. 3

The graphics pipeline 4

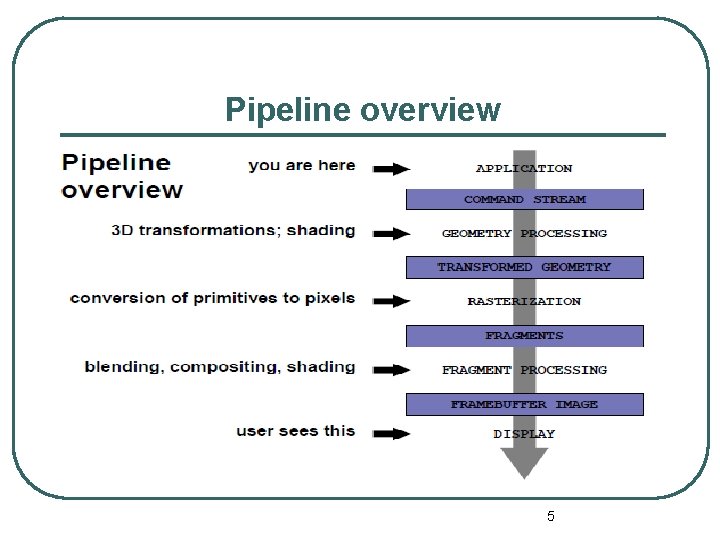
Pipeline overview 5

Primitives 6

Rasterization l First job: enumerate the pixels covered by a primitive • Simple, aliased definition: pixels whose centers fall inside l Second job: interpolate values across the primitive • e. g. , colors computed at vertices • Will see applications later on 7

Rasterizing lines 8

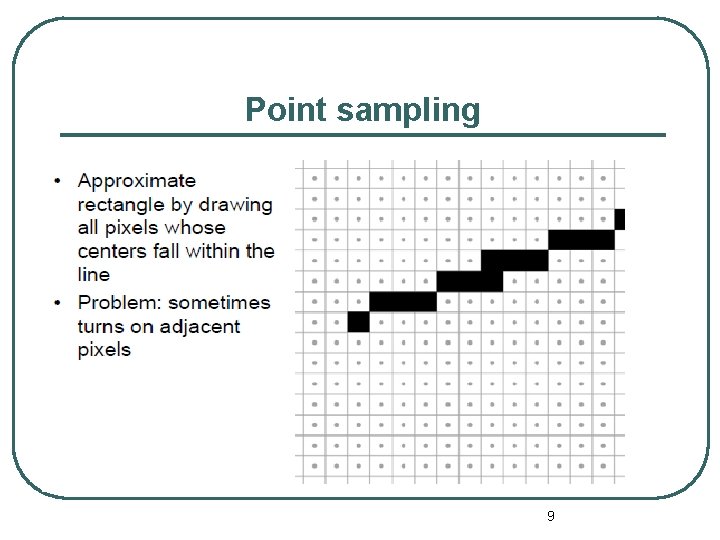
Point sampling 9

Point sampling in action 10

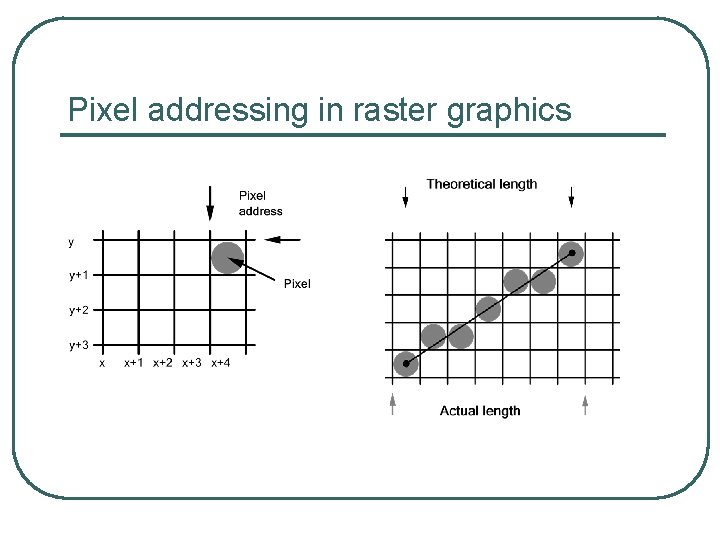
Pixel addressing in raster graphics

Raster conversion algorithms: requirements l visual accuracy l speed

Line drawing algorithms

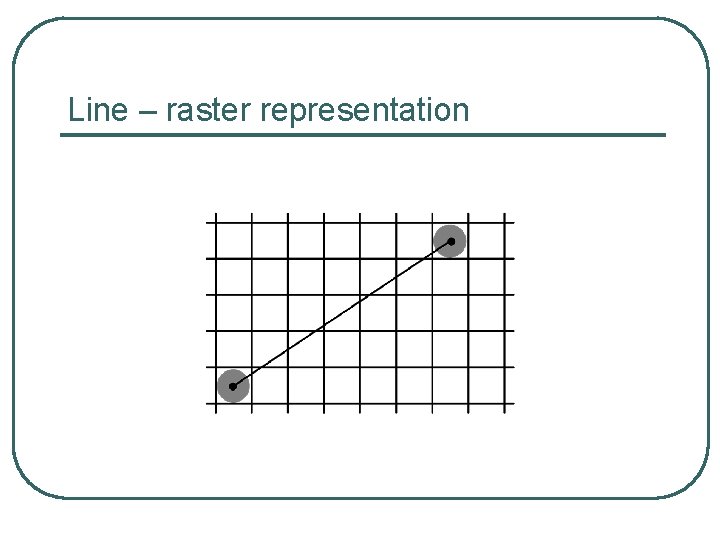
Line – raster representation

How does computer draw line? l l l Screen made of pixels High-level language specifies line System must color pixels

Naïve algorithm for lines l l Line definition: ax+by+c = 0 Also expressed as: y = mx + d • m = slope • d = distance For x=xmin to xmax compute y = m*x+d light pixel (x, y)

Extension by symmetry l Only works with -1 £ m £ 1: m=3 m = 1/3 Extend by symmetry for m > 1

Problems 2 floating-point operations per pixel l Improvements: compute y = m*p+d For x=xmin to xmax l y += m light pixel (x, y) l l Still 1 floating-point operation per pixel Compute in floats, pixels in integers

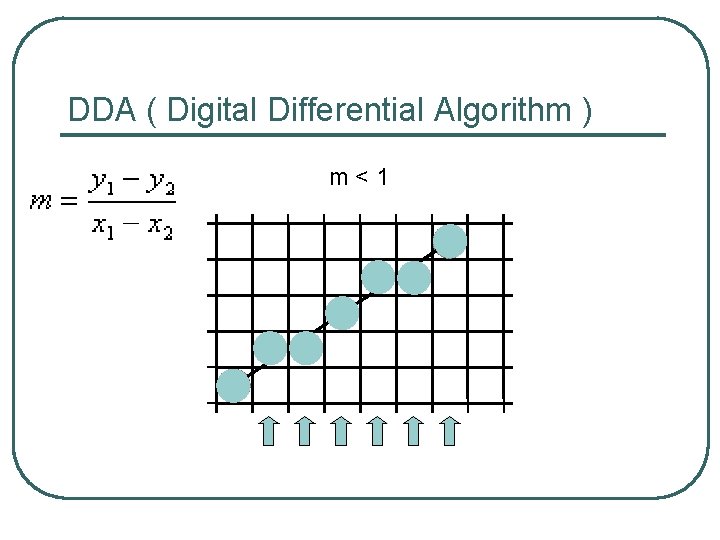
DDA ( Digital Differential Algorithm ) m<1

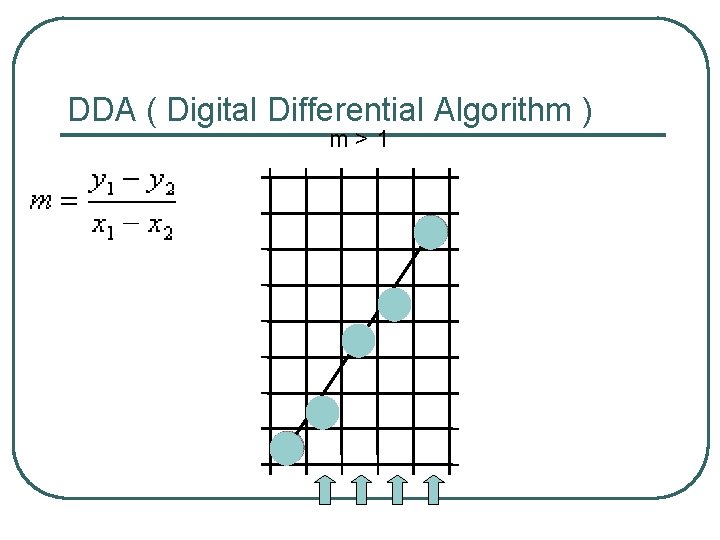
DDA ( Digital Differential Algorithm ) m>1

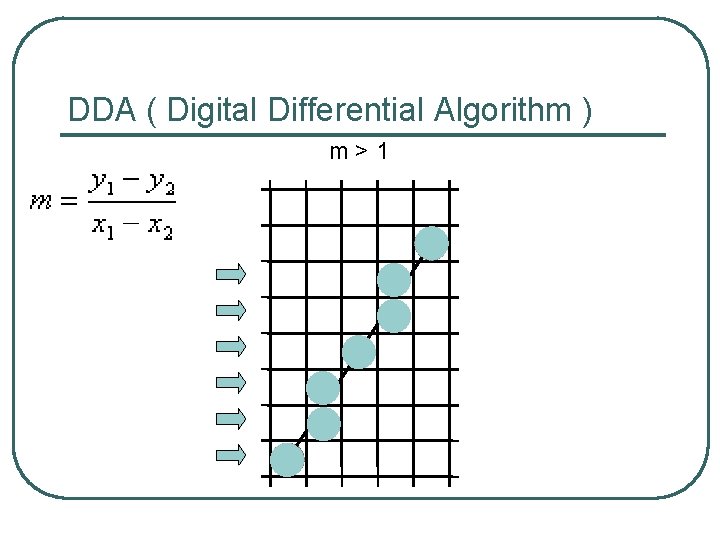
DDA ( Digital Differential Algorithm ) m>1

Digital Differential Algorithm l l l input line endpoints, (x 0, y 0) and (xn, yn) set pixel at position (x 0, y 0) calculate slope m Case |m|≤ 1: repeat the following steps until (xn, yn) is reached: yi+1 = yi + y/ x xi+1 = xi + 1 set pixel at position (xi+1, Round(yi+1)) Case |m|>1: repeat the following steps until (xn, yn) is reached: xi+1 = xi + x/ y yi+1 = yi + 1 set pixel at position (Round(xi+1), yi+1)

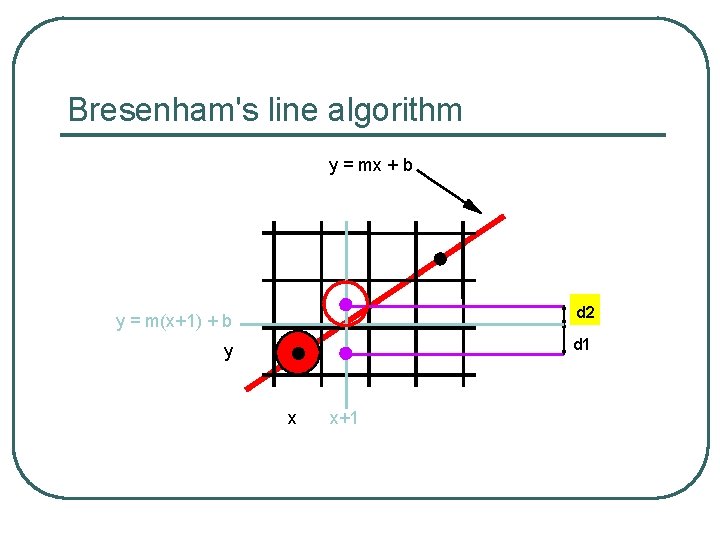
Bresenham's line algorithm y = mx + b y = m(x+1) + b d 2 y d 1 x x+1

Bresenham's line algorithm (slope ≤ 1) l l l input line endpoints, (x 0, y 0) and (xn, yn) calculate x = xn - x 0 and y = yn - y 0 calculate parameter p 0 = 2 y - x set pixel at position (x 0, y 0) repeat the following steps until (xn, yn) is reached: if pi < 0 set the next pixel at position (xi +1, yi ) calculate new pi+1 = pi + 2 y if pi ≥ 0 set the next pixel at position (xi +1, yi + 1 ) calculate new pi+1 = pi + 2( y - x)

DDA versus Bresenham’s Algorithm l l DDA works with floating point arithmetic Rounding to integers necessary l Bresenham’s algorithm uses integer arithmetic Constants need to be computed only once l Bresenham’s algorithm generally faster than DDA l

Circle: naïve algorithm l l Circle equation: x 2+y 2 -r 2 = 0 Simple algorithm: for x = xmin to xmax y = sqrt(r*r - x*x) draw pixel(x, y) l Work by octants and use symmetry

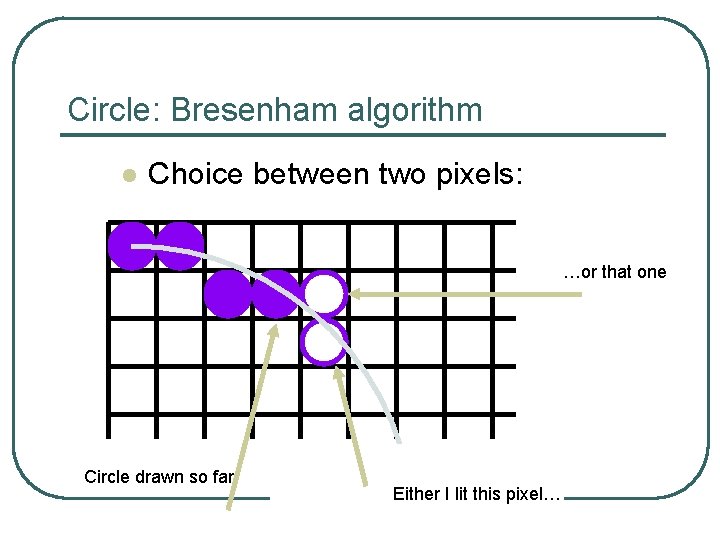
Circle: Bresenham algorithm l Choice between two pixels: …or that one Circle drawn so far Either I lit this pixel…