Image Search query search results 1 Image Search

Image Search query search results 1

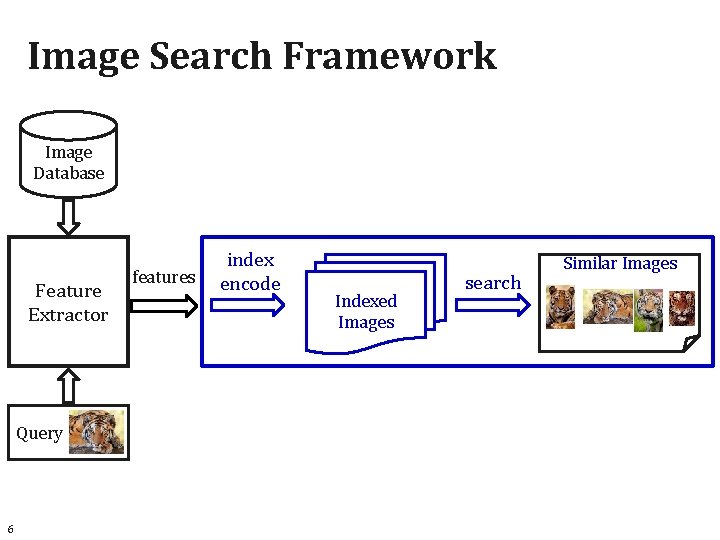
Image Search Framework Image Database Feature Extractor Query 2 features index encode Indexed Images search Similar Images

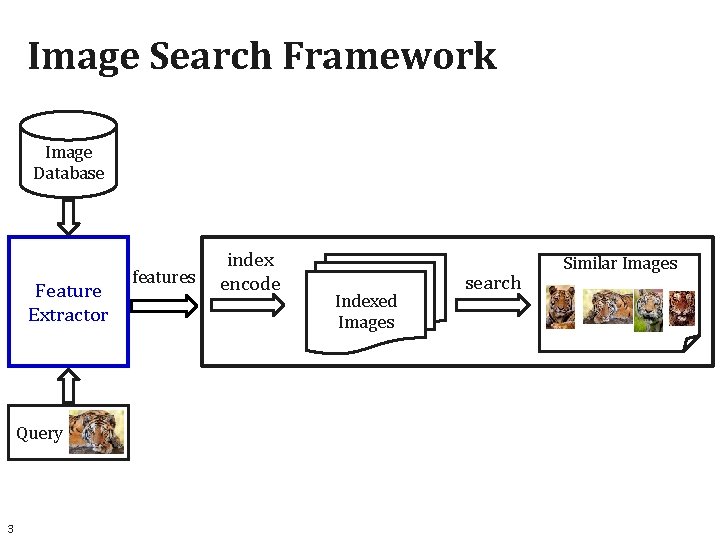
Image Search Framework Image Database Feature Extractor Query 3 features index encode Indexed Images search Similar Images

Image Features • High dimensional vectors that describe images 4

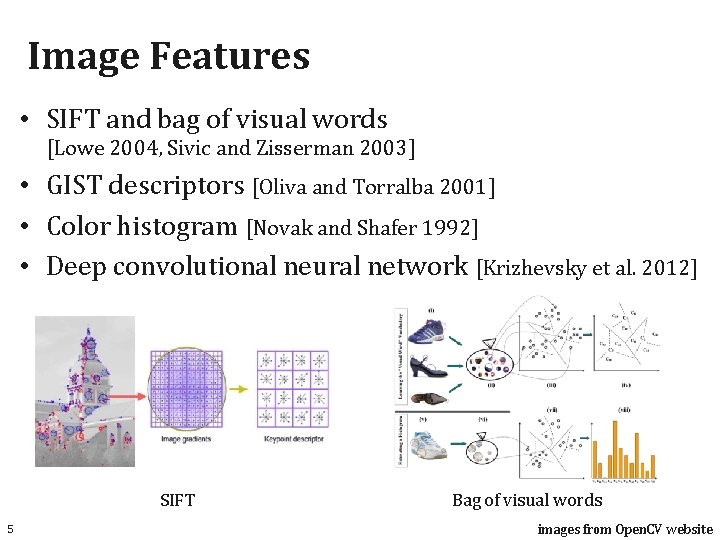
Image Features • SIFT and bag of visual words [Lowe 2004, Sivic and Zisserman 2003] • GIST descriptors [Oliva and Torralba 2001] • Color histogram [Novak and Shafer 1992] • Deep convolutional neural network [Krizhevsky et al. 2012] SIFT 5 Bag of visual words images from Open. CV website

Image Search Framework Image Database Feature Extractor Query 6 features index encode Indexed Images search Similar Images

Challenge Descriptor CNN Dim 1000+ 4000+ 1 item 4 KB+ 16 KB+ 400 GB+ 1. 6 TB+ 100 M items 7 Bag of Words kd-tree [Bentley 1975]

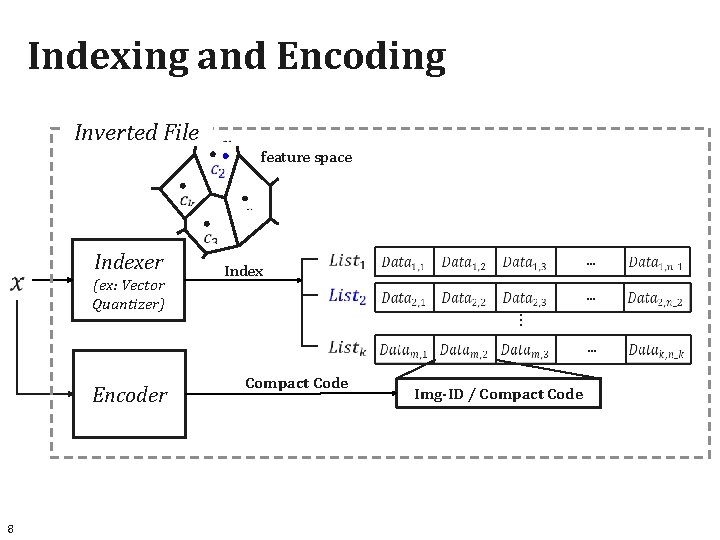
Indexing and Encoding Inverted File feature space Indexer … … … (ex: Vector Quantizer) Index Encoder 8 Compact Code … Img-ID / Compact Code

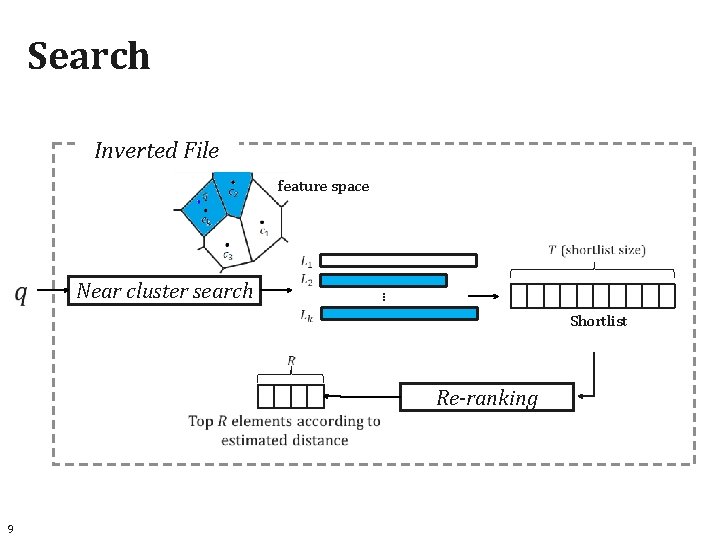
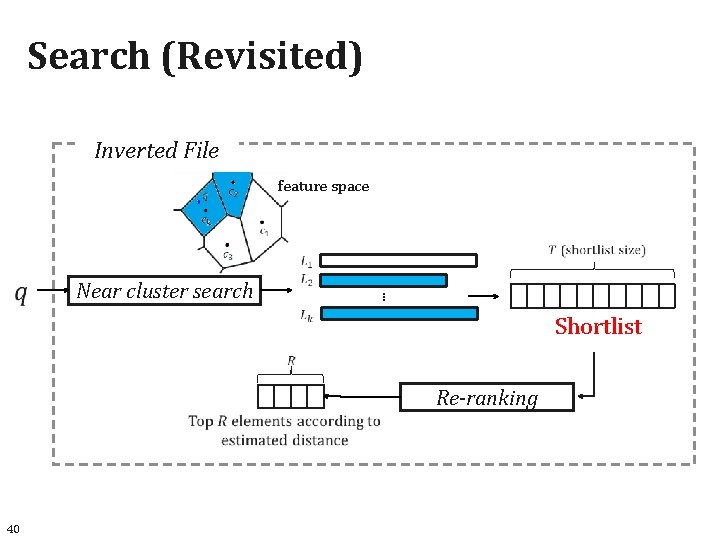
Search Inverted File feature space Near cluster search … Shortlist Re-ranking 9

My Contributions Image Database Feature Extractor Query 10 - Spherical Hashing [CVPR 2012] - Distance Encoded Product Quantization [CVPR 2014] - Accurate Shortlist Computation [ongoing] features index encode Indexed Images search Similar Images

Contents Image Database Feature Extractor Query 11 - Spherical Hashing [CVPR 2012] - Distance Encoded Product Quantization [CVPR 2014] - Accurate Shortlist Computation [ongoing] features index encode Indexed Images search Similar Images

Compact Data Representation • Represent high-dimensional data as compact codes – High compression ratio (scalability) – Fast distance estimation (efficiency) • Research goal – Minimizing reconstruction error (maximize accuracy) of estimated distances • Two popular directions: – Hashing – Product quantization 12

Design Principles • Three design principles of compact code representation from my perspective on the problem: – A) Space Partitioning • How to (geometrically) partition the space. – B) Compact Code Assignment • How to assign a compact code for each partitioned region. – C) Distance Estimation • How to define a distance between compact codes for estimation of their original distance. 13

Spherical Hashing IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), 2012 14

Prior Hashing Methods • Partitioning: Hyper-planes 0 1 0 • Assignment: Projection 1 010 000 110 011 100 • Distance estimation: Hamming distance – the number of hyper-planes between two points – can be efficiently computable with the XOR operation 15 0 1

Related Work – Hashing 16 Random projection [Indyk and Matwani, STOC 1998] Spectral graph partitioning [Weiss et al. , NIPS 2008] Principal Component Analysis [Gordo and Perronnin, CVPR 2011] Independent Component Analysis [He et al. , CVPR 2011] Large margin hyper-planes [Joly and Perronnin, CVPR 2011] Optimally rotated PCA [Gong and Lazebnik, CVPR 2011] Some figures are from authors.

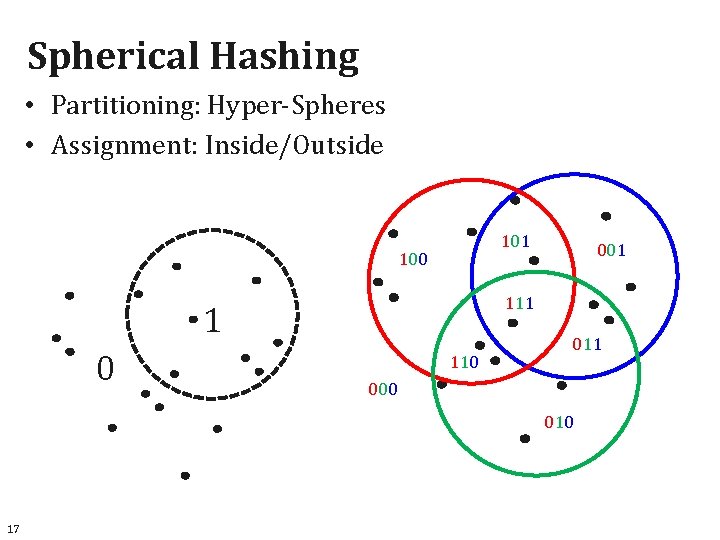
Spherical Hashing • Partitioning: Hyper-Spheres • Assignment: Inside/Outside 101 100 111 1 0 001 110 011 000 010 17

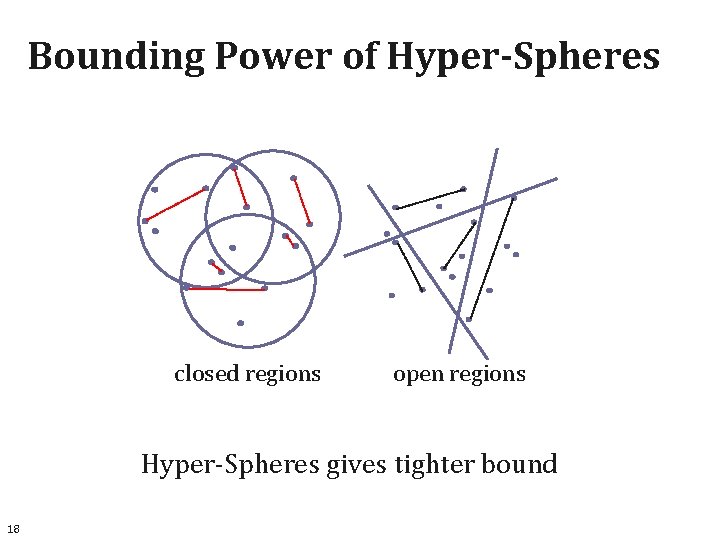
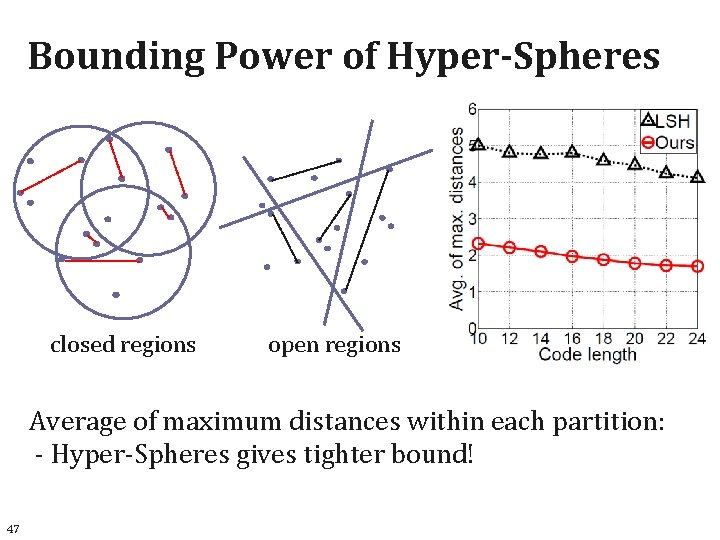
Bounding Power of Hyper-Spheres closed regions open regions Hyper-Spheres gives tighter bound 18

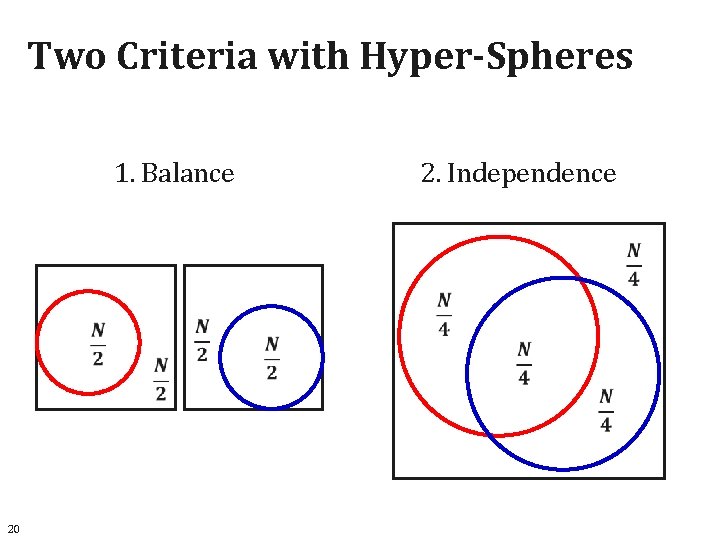
Two Criteria for Hashing [Yeiss 2008, He 2011] Developed for projection-based methods: 1. Balanced partitioning 2. Independence < 19

Two Criteria with Hyper-Spheres 1. Balance 2. Independence 20

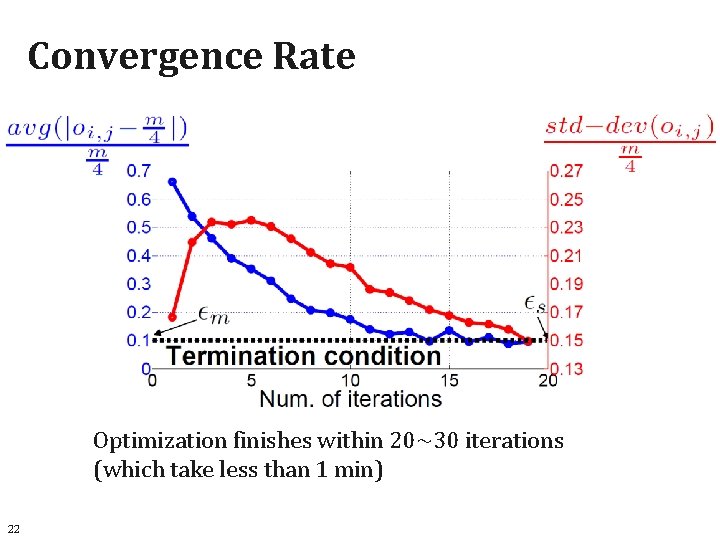
Iterative Optimization Repeat step 1, 2 until convergence. 21

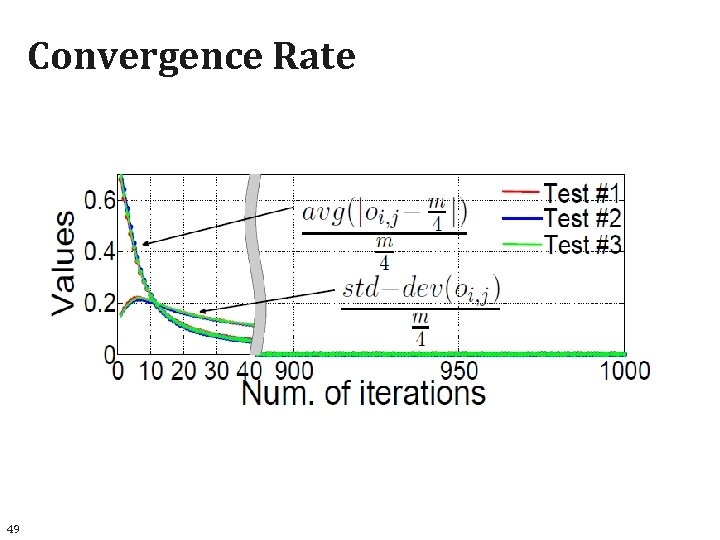
Convergence Rate Optimization finishes within 20~30 iterations (which take less than 1 min) 22

Distance Estimation Hamming distance # of common bounding hyper-spheres 23 bounded by 1 hyper-sphere bounded by 2 hyper-spheres bounded by 3 hyper-spheres

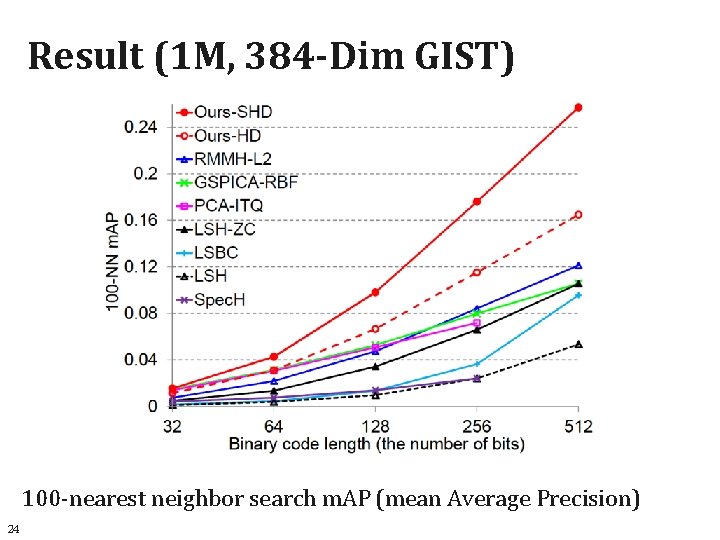
Result (1 M, 384 -Dim GIST) 100 -nearest neighbor search m. AP (mean Average Precision) 24

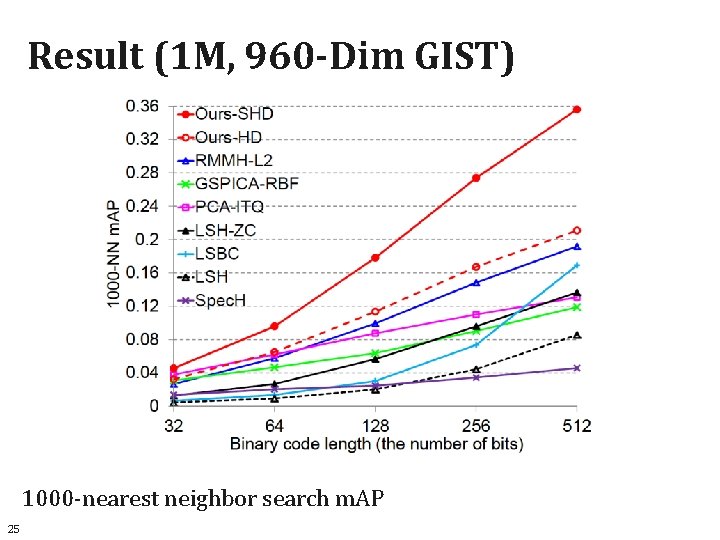
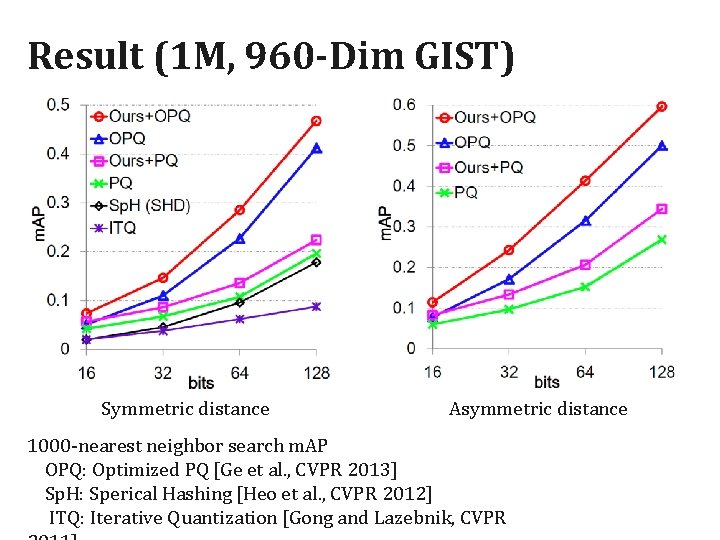
Result (1 M, 960 -Dim GIST) 1000 -nearest neighbor search m. AP 25

Result (1 M, 8192 -Dim VLAD) 1000 -nearest neighbor search m. AP 26

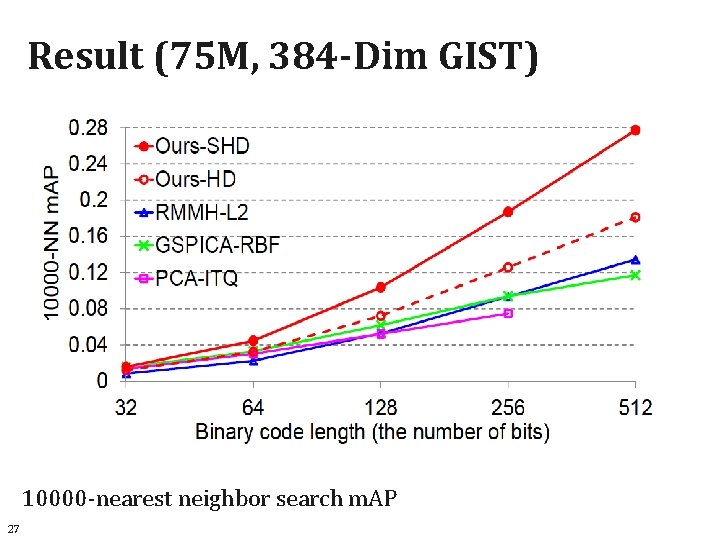
Result (75 M, 384 -Dim GIST) 10000 -nearest neighbor search m. AP 27

Distance Encoded Product Quantization IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), 2014 28

Product Quantization [Jegou et al. , TPAMI 2011] - Partitioning: Subspaces and Quantization 01 Quantization . . . - Assignment: Cluster index 11 Quantization Subspace #1 00 01 Quantization 11 . . 00 Original space 01 Quantization 11 Subspace #M 29 10 10 01 11

Product Quantization [Jegou et al. , TPAMI 2011] Subspace #1 Asymmetric distance +. . . Actual distance Symmetric distance + Subspace #M 30 Left figure is from [Jegou et al. , TPAMI 2011]

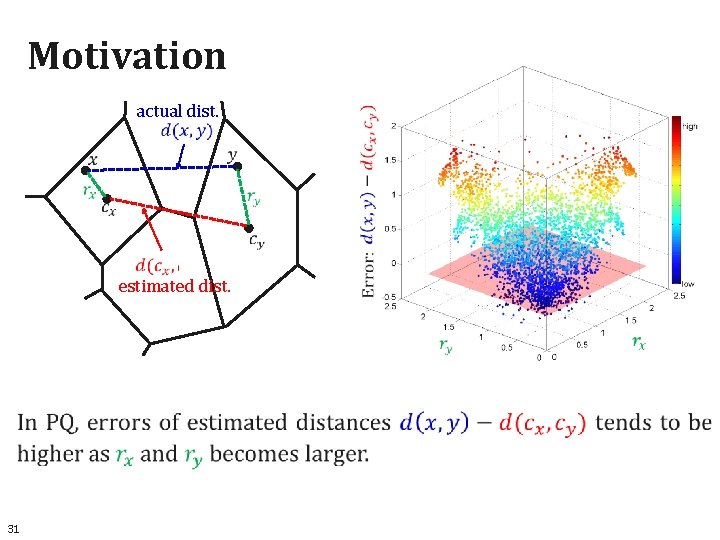
Motivation actual dist. estimated dist. 31

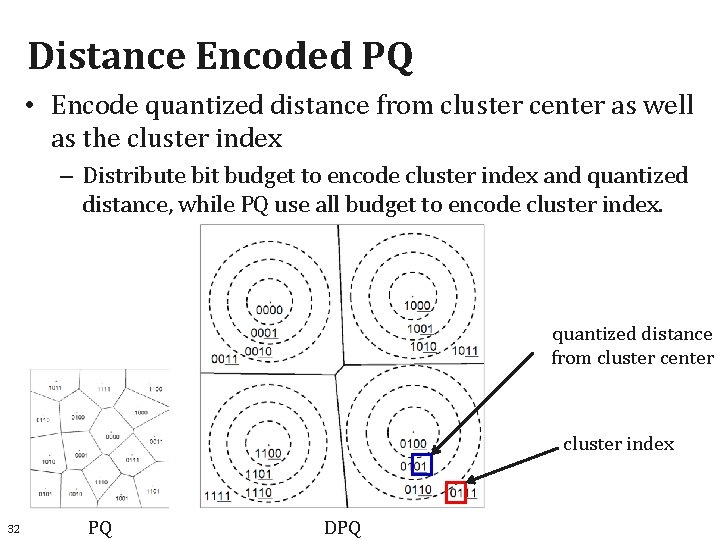
Distance Encoded PQ • Encode quantized distance from cluster center as well as the cluster index – Distribute bit budget to encode cluster index and quantized distance, while PQ use all budget to encode cluster index. quantized distance from cluster center cluster index 32 PQ DPQ

Orthogonality in High Dim. Space In high dimensional space, two randomly chosen vectors are highly likely to be orthogonal*. orthogonality 33 *Mathematical foundations for the information age [J. Hopcroft, 2010]

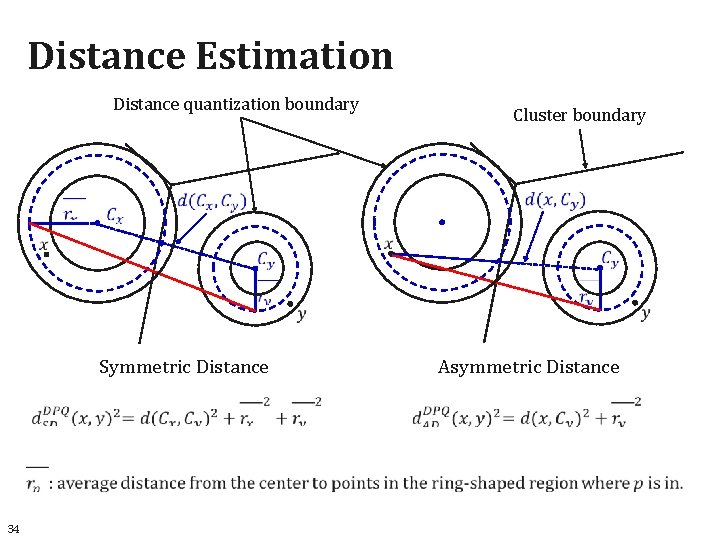
Distance Estimation Distance quantization boundary Cluster boundary Asymmetric Distance Symmetric Distance 34

Result (1 M, 960 -Dim GIST) Symmetric distance Asymmetric distance 1000 -nearest neighbor search m. AP OPQ: Optimized PQ [Ge et al. , CVPR 2013] Sp. H: Sperical Hashing [Heo et al. , CVPR 2012] ITQ: Iterative Quantization [Gong and Lazebnik, CVPR

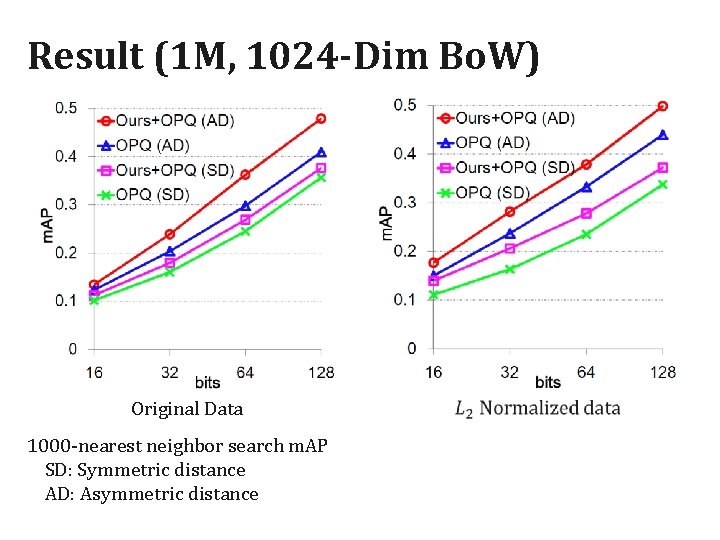
Result (1 M, 1024 -Dim Bo. W) Original Data 1000 -nearest neighbor search m. AP SD: Symmetric distance AD: Asymmetric distance

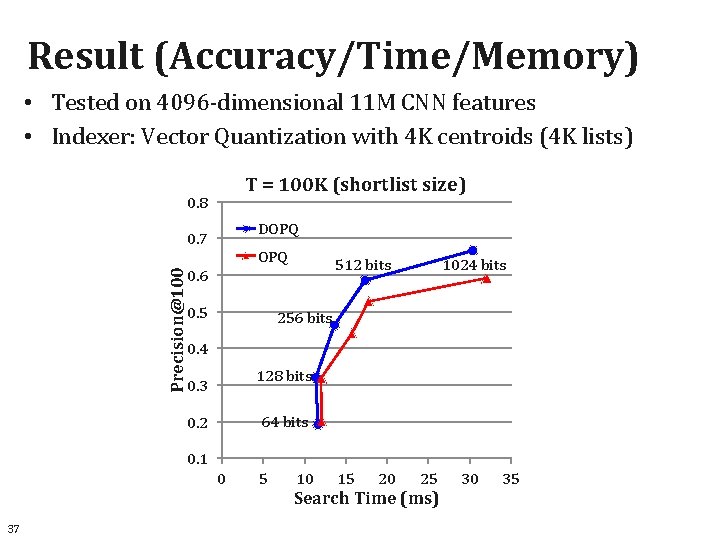
Result (Accuracy/Time/Memory) • Tested on 4096 -dimensional 11 M CNN features • Indexer: Vector Quantization with 4 K centroids (4 K lists) T = 100 K (shortlist size) 0. 8 DOPQ Precision@100 0. 7 OPQ 0. 5 1024 bits 512 bits 0. 6 256 bits 0. 4 128 bits 0. 3 64 bits 0. 2 0. 1 0 5 10 15 20 25 Search Time (ms) 37 30 35

Image Search Demo • 11 M images from Flickr • 4096 dimensional image features – convolutional neural network • Developed during 1 st internship at Adobe 38

Contents Image Database Feature Extractor Query 39 - Spherical Hashing [CVPR 2012] - Distance Encoded Product Quantization [CVPR 2014] - Accurate Shortlist Computation [ongoing] features index encode Indexed Images search Similar Images

Search (Revisited) Inverted File feature space Near cluster search … Shortlist Re-ranking 40

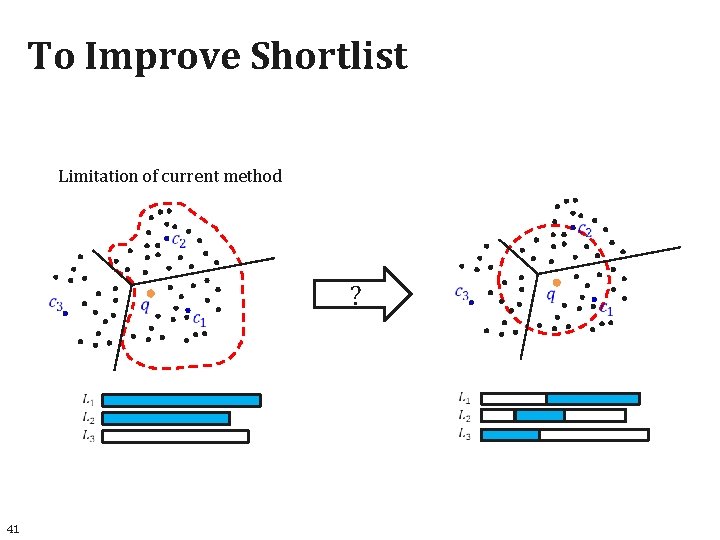
To Improve Shortlist Limitation of current method 41 ?

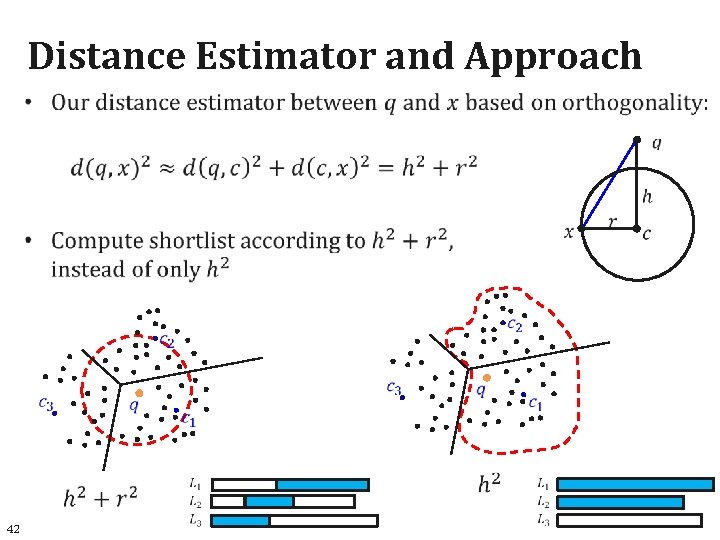
Distance Estimator and Approach 42

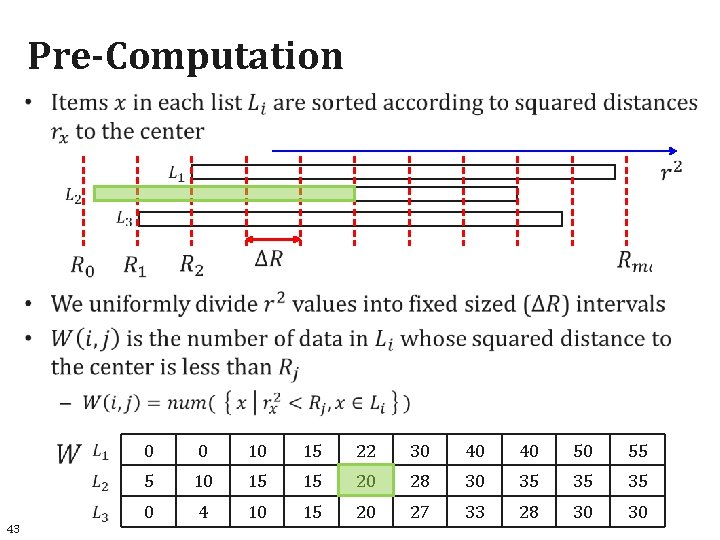
Pre-Computation 43 0 0 10 15 22 30 40 40 50 55 5 10 15 15 20 28 30 35 35 35 0 4 10 15 20 27 33 28 30 30

Shortlist Computation (Runtime) 44 0 0 10 15 22 30 40 40 50 55 5 10 15 15 20 28 30 35 35 35 0 4 10 15 20 27 33 28 30 30

Shortlist Comp. based on H 2 R 2 (Runtime) 45 0 0 10 15 22 30 40 40 50 55 5 10 15 15 20 28 30 35 35 35 0 4 10 15 20 27 33 28 30 30 35 50 83

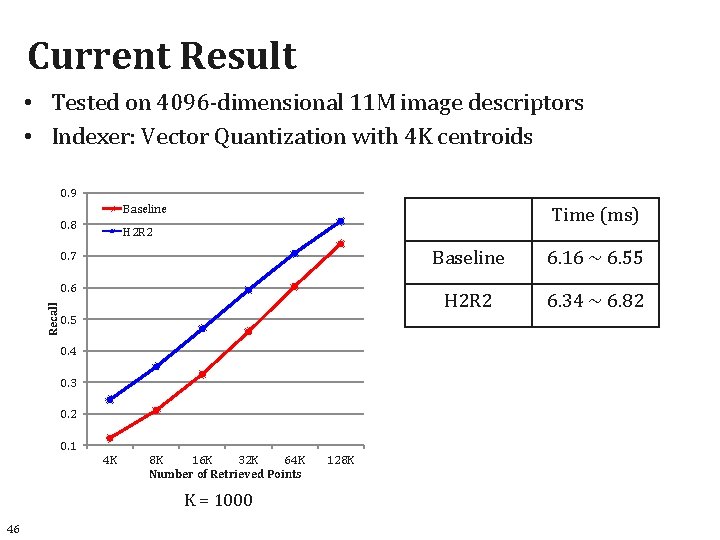
Current Result • Tested on 4096 -dimensional 11 M image descriptors • Indexer: Vector Quantization with 4 K centroids 0. 9 Baseline 0. 8 Time (ms) H 2 R 2 0. 7 Recall 0. 6 0. 5 0. 4 0. 3 0. 2 0. 1 4 K 8 K 16 K 32 K 64 K Number of Retrieved Points K = 1000 46 128 K Baseline 6. 16 ~ 6. 55 H 2 R 2 6. 34 ~ 6. 82

Bounding Power of Hyper-Spheres closed regions open regions Average of maximum distances within each partition: - Hyper-Spheres gives tighter bound! 47

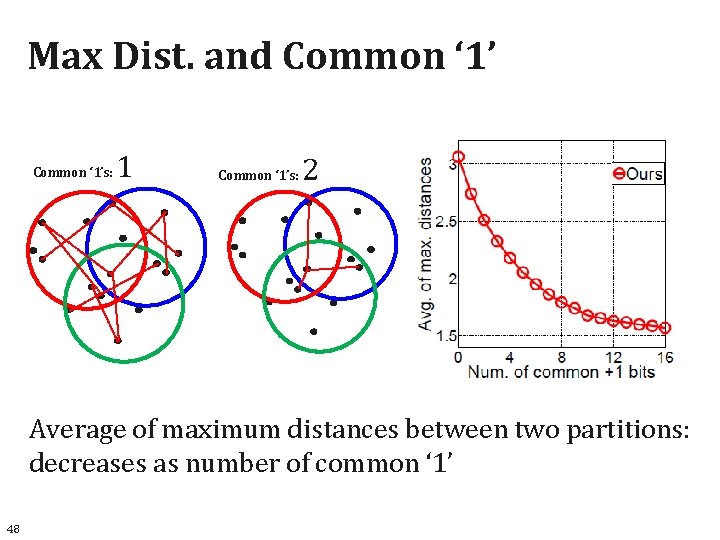
Max Dist. and Common ‘ 1’s: 1 Common ‘ 1’s: 2 Average of maximum distances between two partitions: decreases as number of common ‘ 1’ 48

Convergence Rate 49

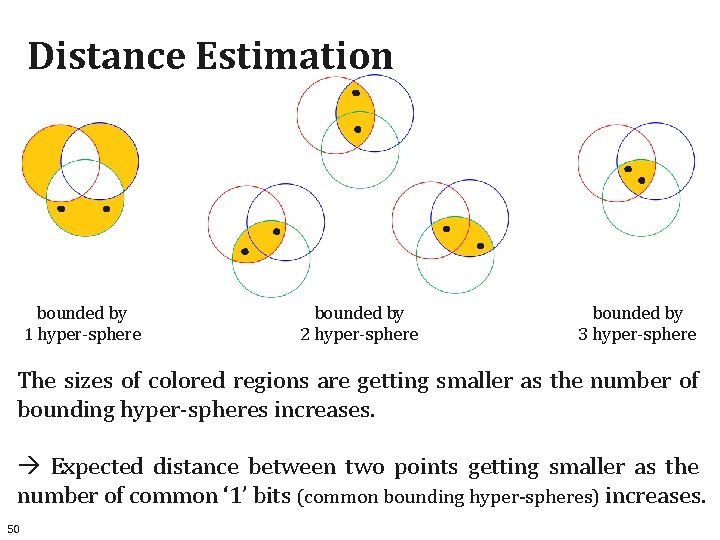
Distance Estimation bounded by 1 hyper-sphere bounded by 2 hyper-sphere bounded by 3 hyper-sphere The sizes of colored regions are getting smaller as the number of bounding hyper-spheres increases. Expected distance between two points getting smaller as the number of common ‘ 1’ bits (common bounding hyper-spheres) increases. 50

Spherical Hamming Distance (SHD) 51

Orthogonality in High-Dim Space* 52 * Detailed proof is given in the course notes of mathematical foundations for the information age [J. Hopcroft, 2010]