Image Sampling and Quantization Representing Digital Images The



















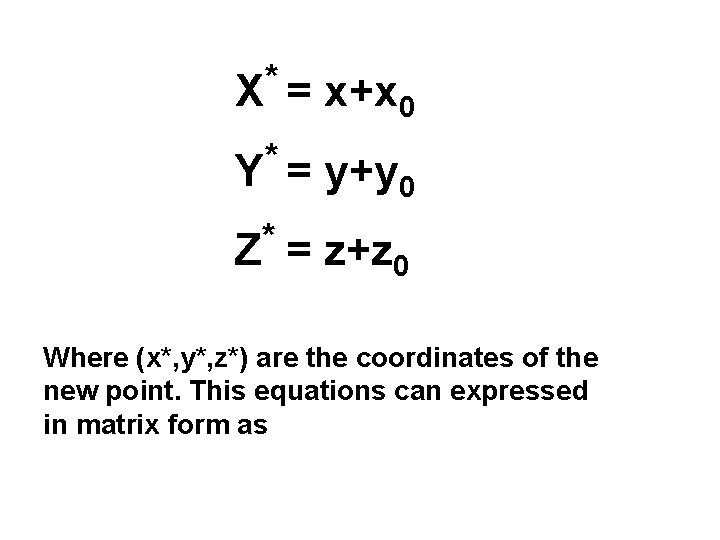
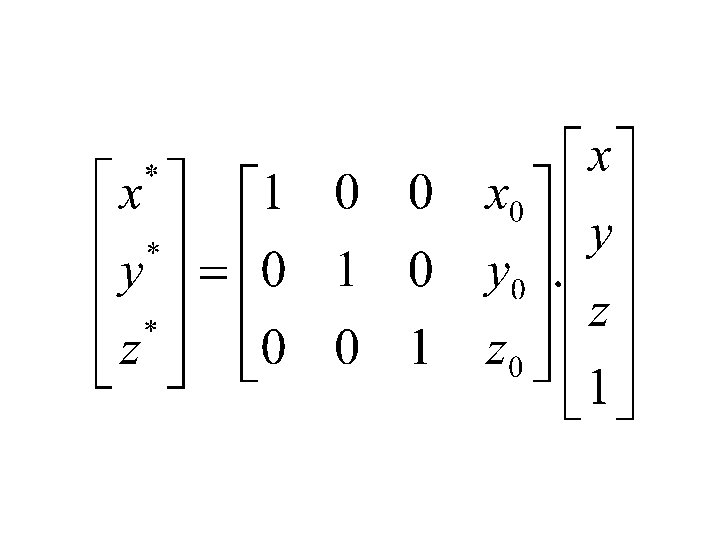










- Slides: 55

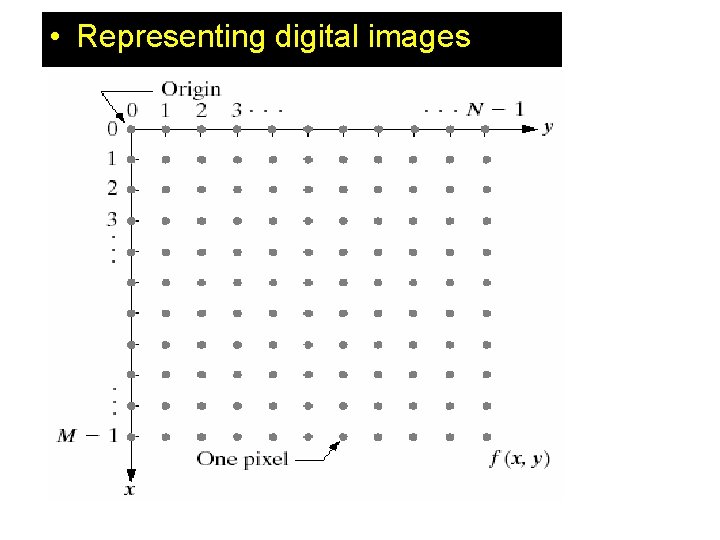
Image Sampling and Quantization • Representing Digital Images The notation introduced in the preceding paragraph allows us to write the complete M*N digital image in the following compact matrix. • This digitization process requires decisions about values for M, N, and for the number, L, of discrete gray levels allowed for each pixel. • There are no requirements on M and N, other than that they have to be positive integers. • Due to processing, storage, and sampling hardware considerations, the number of gray levels typically is an integer power of 2: L = 2 k.

• Representing digital images

Each pixel have an value equal f that is gray value

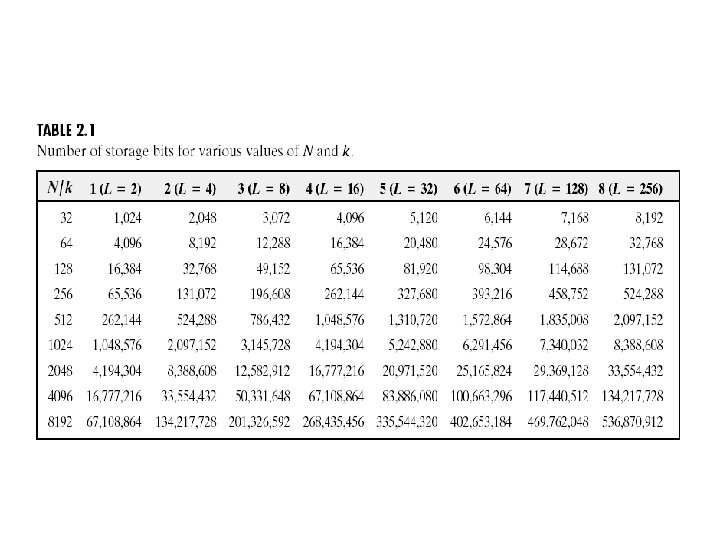
Image Sampling and Quantization – The number, b, of bits required to store a digitized image is b = M * N * k. When M=N, this equation becomes b = N 2 k. Table 2. 1 shows the number of bits required to store square images with various values of N and k.


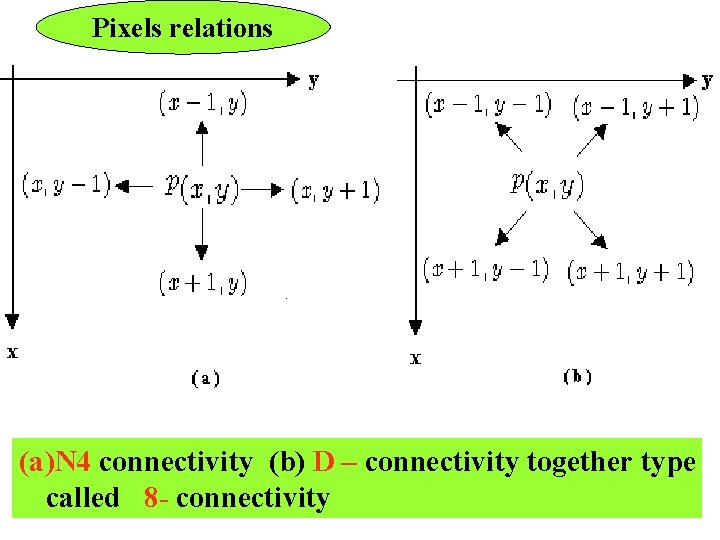
Pixels relations (a)N 4 connectivity (b) D – connectivity together type called 8 - connectivity

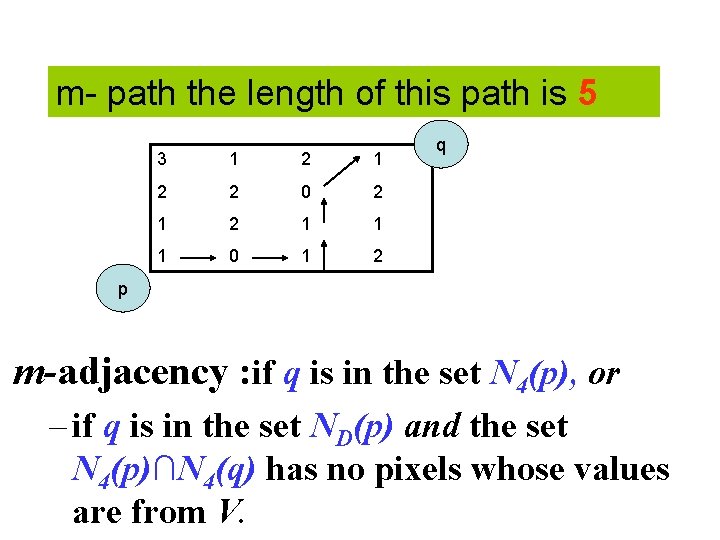
• 4 -adjacency: if q is in the set N 4(p). • 8 -adjacency: if q is in the set N 8(p). • m-adjacency: if – if q is in the set N 4(p), or – if q is in the set ND(p) and the set N 4(p)∩N 4(q) has no pixels whose values are from V.

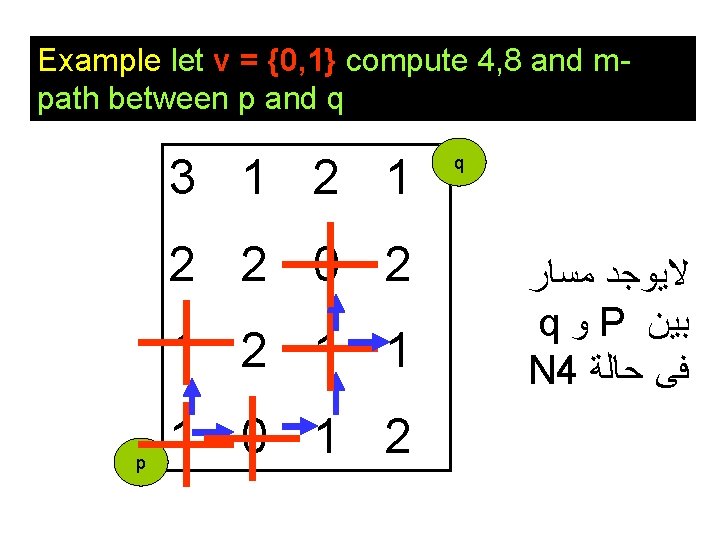
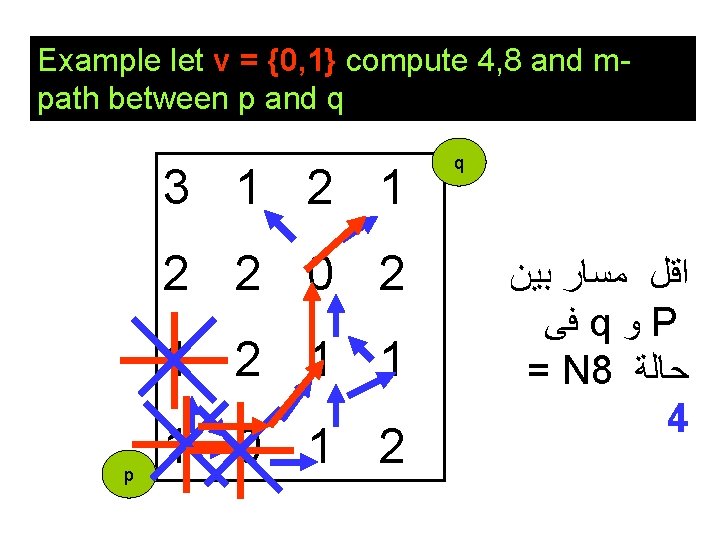
Example let v = {0, 1} compute 4, 8 and mpath between p and q 3 1 2 2 0 2 1 1 p 1 0 1 2 q ﻻﻳﻮﺟﺪ ﻣﺴﺎﺭ q ﻭ P ﺑﻴﻦ N 4 ﻓﻰ ﺣﺎﻟﺔ

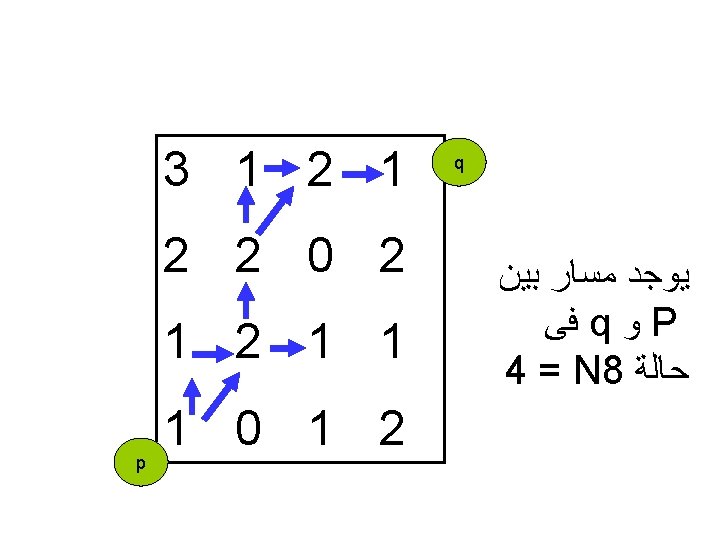
Example let v = {0, 1} compute 4, 8 and mpath between p and q 3 1 2 2 0 2 1 1 p 1 0 1 2 q ﺍﻗﻞ ﻣﺴﺎﺭ ﺑﻴﻦ ﻓﻰ q ﻭ P = N 8 ﺣﺎﻟﺔ 4

m- path the length of this path is 5 3 1 2 2 0 2 1 1 1 0 1 2 q p m-adjacency : if q is in the set N 4(p), or – if q is in the set ND(p) and the set N 4(p)∩N 4(q) has no pixels whose values are from V.

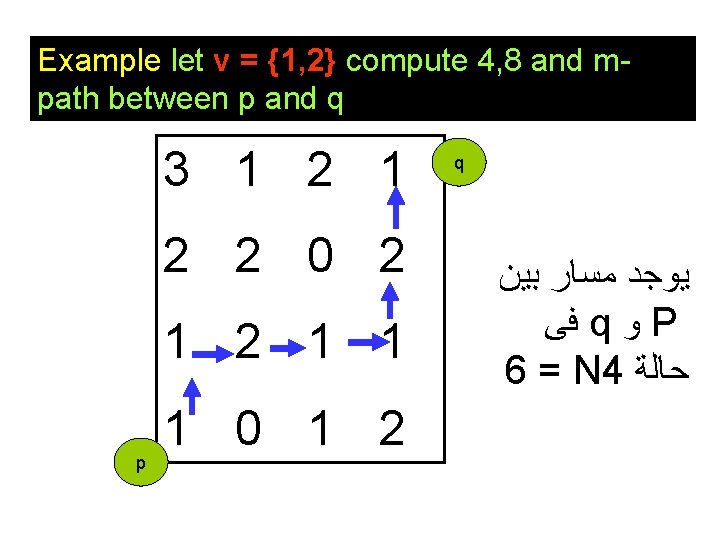
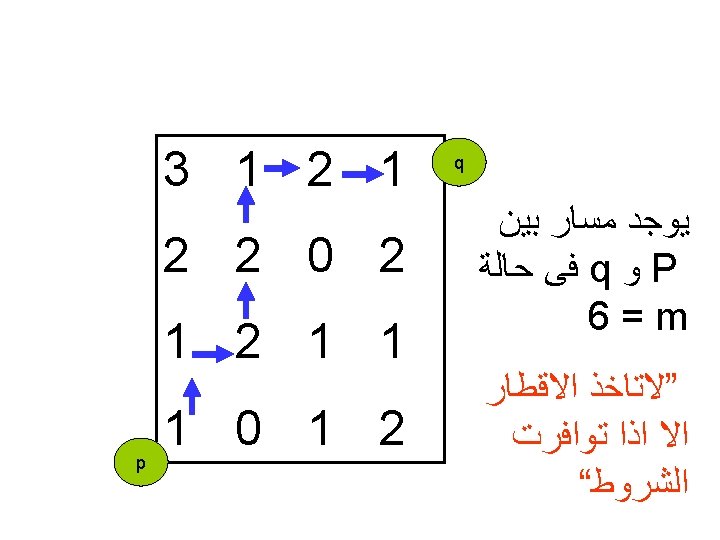
Example let v = {1, 2} compute 4, 8 and mpath between p and q 3 1 2 2 0 2 1 1 p 1 0 1 2 q ﻳﻮﺟﺪ ﻣﺴﺎﺭ ﺑﻴﻦ ﻓﻰ q ﻭ P 6 = N 4 ﺣﺎﻟﺔ



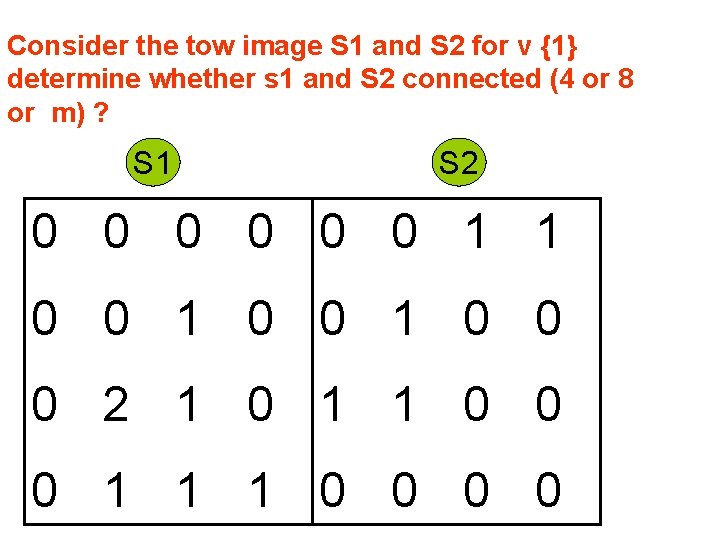
Consider the tow image S 1 and S 2 for v {1} determine whether s 1 and S 2 connected (4 or 8 or m) ? S 1 S 2 0 0 0 1 1 0 0 0 2 1 0 1 1 0 0 0 1 1 1 0 0

S 1 and S 2 are not 4 - connected because q is not in set N 4(p), S 1 and S 2 are 8 - connected because q is in set N 8(p), S 1 and S 2 are m- connected because q is in set ND(p) and set N 4(p) intersection N 4(q) is empty S 1 S 2 0 0 0 1 1 0 0 q 0 2 1 0 1 1 0 0 0 1 1 1 0 0 p

Labeling of connected components Scan an image pixel by pixel from left to right and form top to bottom 4 -connected components t * * r * p

When we get p points r and t have already been countered ( and label if they were 1’s ) * If the value of p=0 then move on the next scanning position • If the value of p=1 then if r=0 and t=0 then assign a new label to p else

If r=1 ant t=0 then assign the label of r to p Else If r=0 and to p t=1 then assign the value t Else if r =1 and t=1 and have different label then assign one of the label to p

Note ( that the two label are equivalent ) else If r=1 ant t=1 and have the same e label then assign that label to p

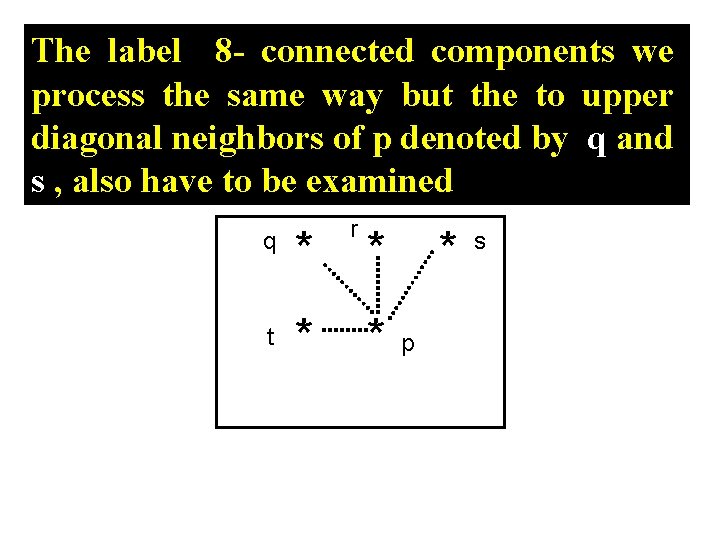
The label 8 - connected components we process the same way but the to upper diagonal neighbors of p denoted by q and s , also have to be examined q * t * r * * * p s

Relations , equivalence and transitive closure A binary (two) relation R on a set A is a set of pairs of elements from A For example the set of pair of point A = { p 1 , p 2, p 3 , p 4 } arranged as p 1 p 2 p 3 p 4

And define the relation 4 - connected in case R is the set of pairs of point A that are 4 - connected that is R = {( p 1 , p 2) , (p 2, p 1) , (p 1, p 3) , (p 3, p 1) } A binary relation R over set A is said to be

(A) reflexive if for each a in A , a R a (b) symmetric if for each a and b in A , a R b implies b R a , and (c) transitive if for a, b and c in in A , a R b and b R c implies a R c A relation satisfying these three properties is called equivalence relation

Distance measures For pixels p , q and z with coordinates (x, y) , (s, t) and (u, v) respectively , D is a distance function or metric if

The Euclidean distance between p and q define as: The 4 - distance also called city block distance between p and q is defines as

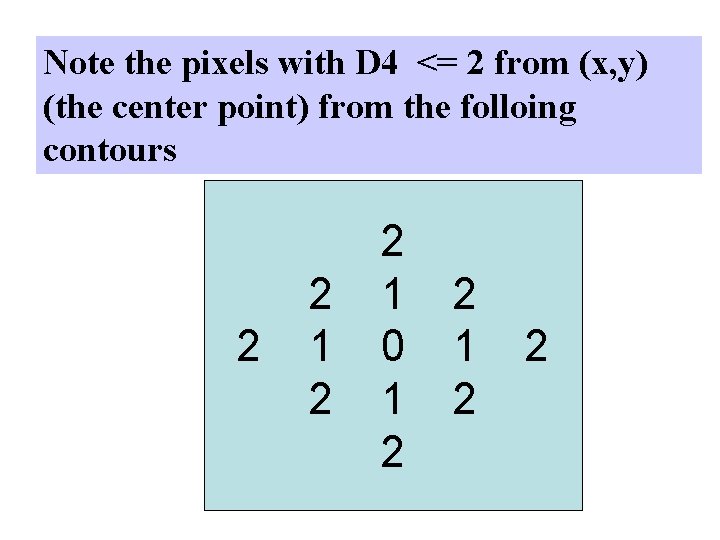
Note the pixels with D 4 <= 2 from (x, y) (the center point) from the folloing contours 2 2 1 0 1 2 2

the pixels with D 4 = 1 are the 4 neighbors of (x, y) the 8 - distance (also called chessboard distance between p and q defined as:

Note the pixels with D 8 <= 2 from (x, y) (the center point) from the folloing contours 2 2 2 1 1 1 2 2 1 0 1 2 2 1 1 1 2 2 2

the pixels with D 8 = 1 are the 8 neighbors of (x, y) For m connectivity the value of distance ( length of the path) between two pixels depends on the values of the pixels along the path for instance consider the following arrangement of pixels

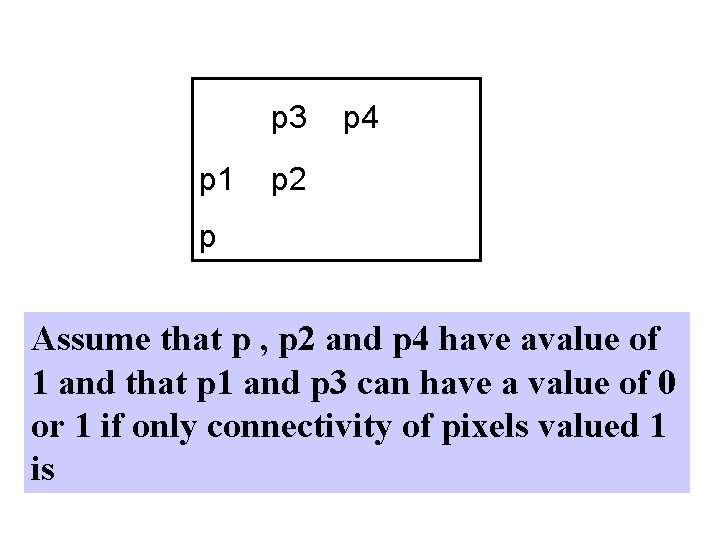
p 3 p 1 p 4 p 2 p Assume that p , p 2 and p 4 have avalue of 1 and that p 1 and p 3 can have a value of 0 or 1 if only connectivity of pixels valued 1 is

Allowed and p 1 and p 3 are 0 , the mdistance between p and p 4 is 2 0 p 3 0 p 1 1 p 2 1 p 4

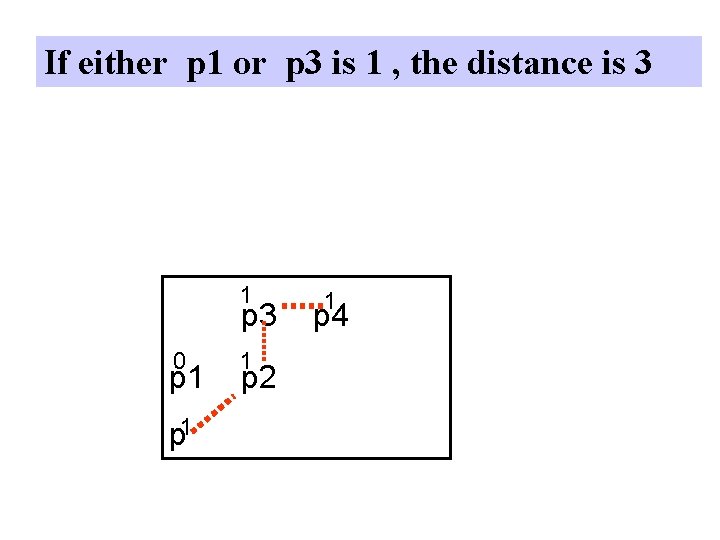
If either p 1 or p 3 is 1 , the distance is 3 1 p 3 0 p 1 1 p 2 1 p 4

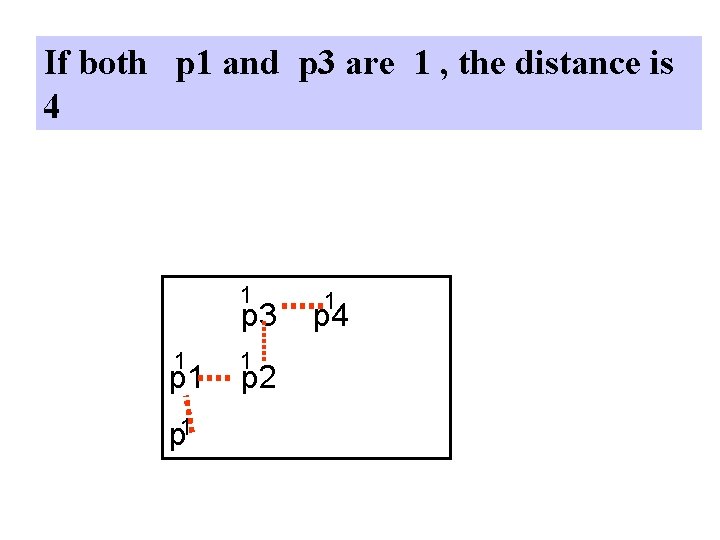
If both p 1 and p 3 are 1 , the distance is 4 1 p 3 1 p 1 1 p 2 1 p 4

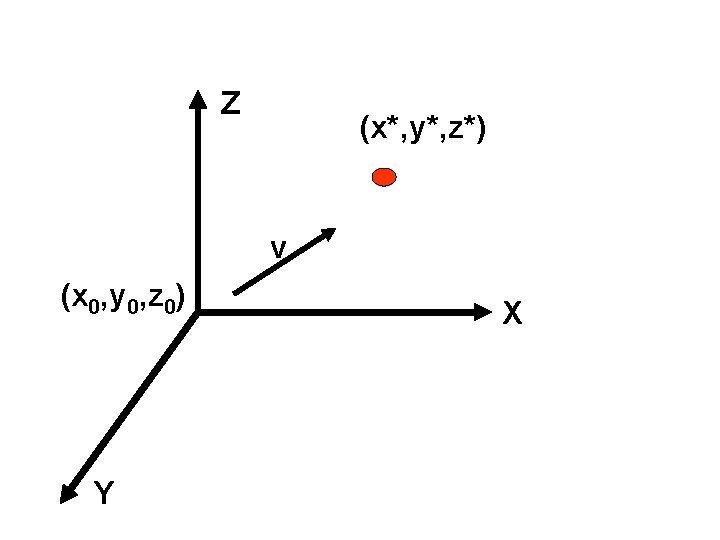
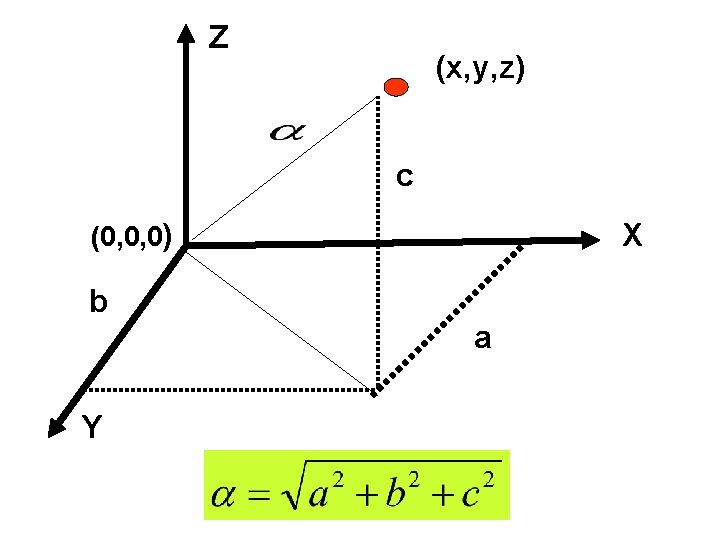
Image geometry Some basic transformation Translation To translate a point with coordinates (x, y, z) to a new location by using displacements (x 0, y 0, z 0) the translation is accomplished by using the equations:

Z (x*, y*, z*) v (x 0, y 0, z 0) Y X
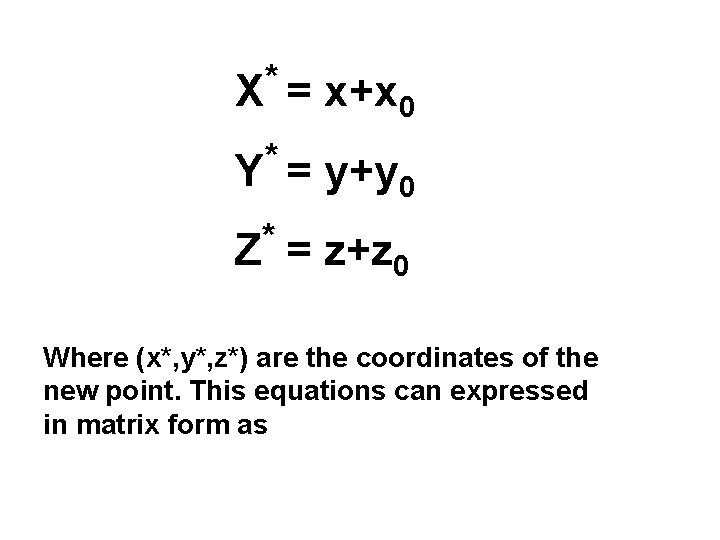
* X = x+x 0 * Y = y+y 0 * Z = z+z 0 Where (x*, y*, z*) are the coordinates of the new point. This equations can expressed in matrix form as
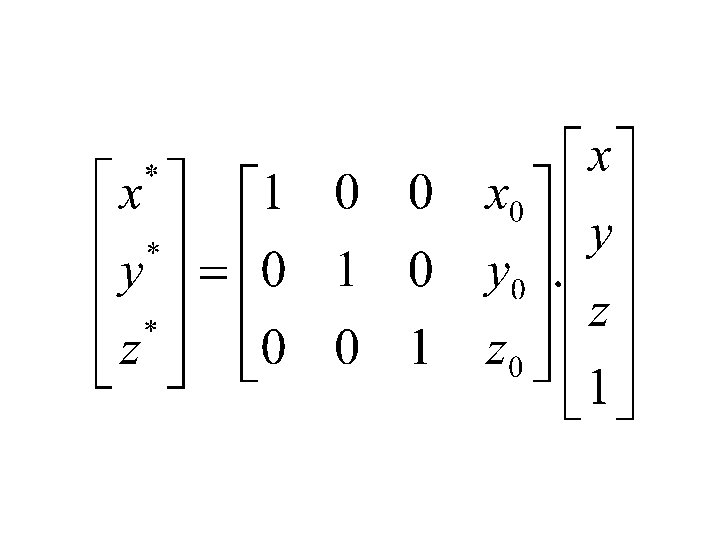

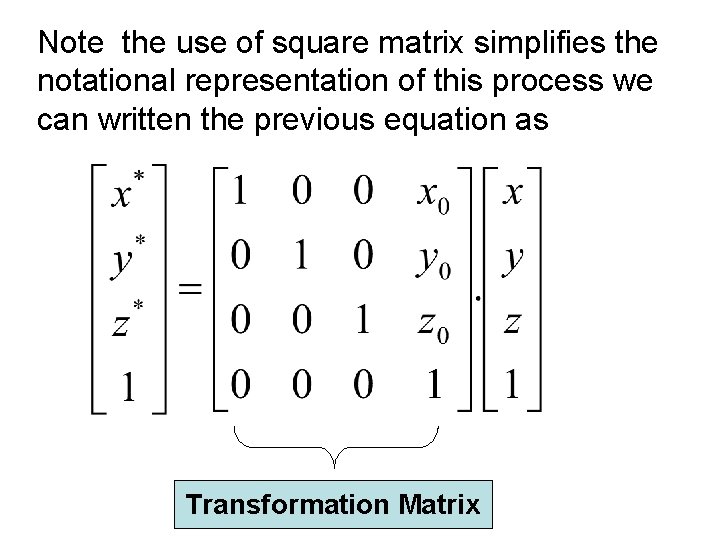
Note the use of square matrix simplifies the notational representation of this process we can written the previous equation as Transformation Matrix

Similarly to translate the point (x, y) to a new point x* = x + x 0 y* = y + y 0 Can be expressed in matrix form as:

Scaling by factors sx, sy and sz along the X, Y and Z axes is given by thr transformation matrix

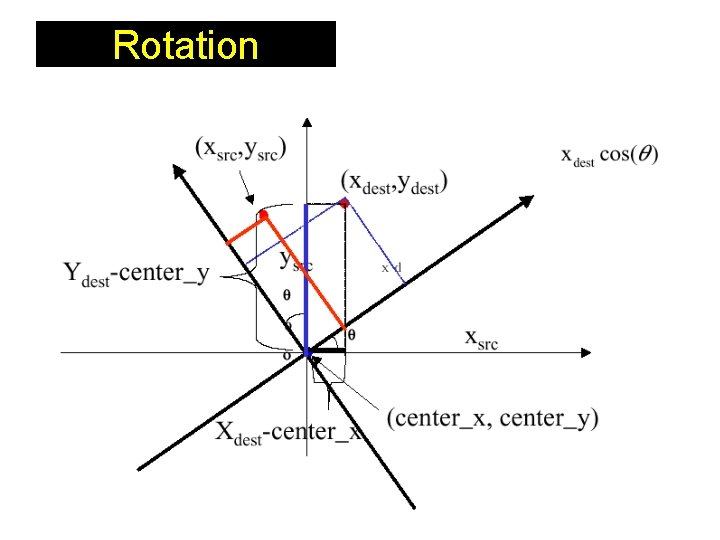
Rotation in 3 D is more complex than 2 D. In 2 D a rotation is prescribed by an angle of rotation and center of rotation P 3 D rotation require the prescription of an angle of rotation and an axis of rotation.

Rotation


Rotation a bout Z axis (x*, y*, z*) = Where (x, y, z)

Rotation a bout Z axis in matrix form

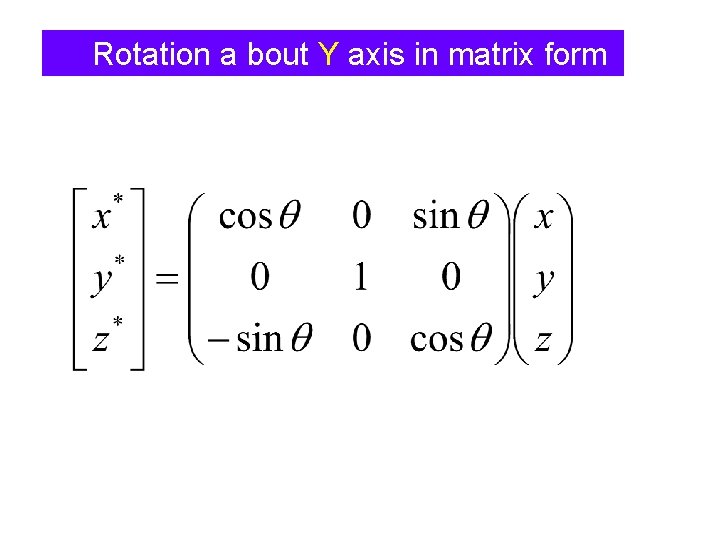
Rotation a bout Y axis (x*, y*, z*) = Where (x, y, z)

Rotation a bout Y axis in matrix form

Rotation a bout X axis (x*, y*, z*) = Where (x, y, z)

Rotation a bout X axis in matrix form

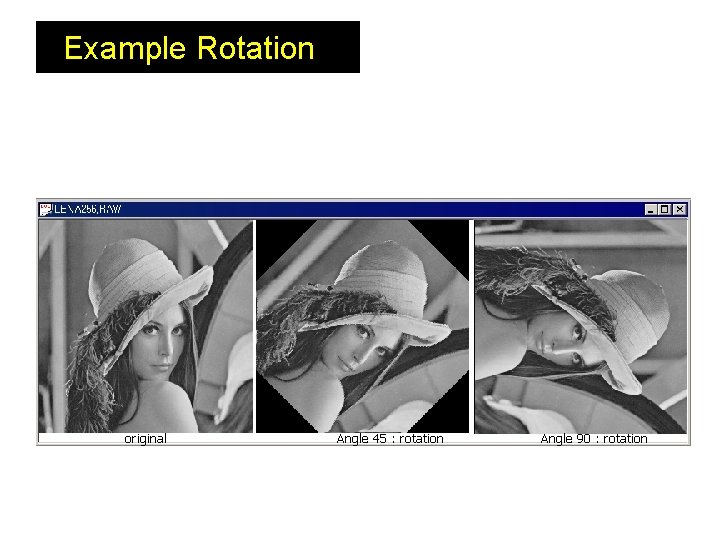
Example Rotation original Angle 45 : rotation Angle 90 : rotation

Example : Rotation & scaling

Example Translation original X 30, y 45 translation

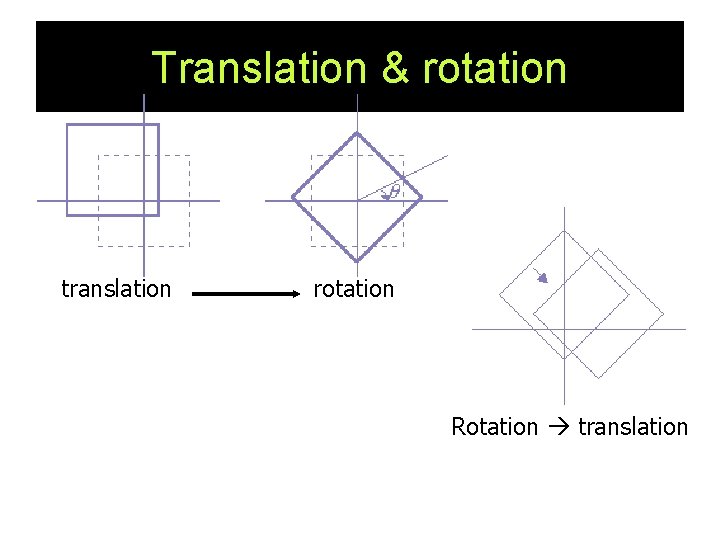
Translation & rotation translation rotation Rotation translation

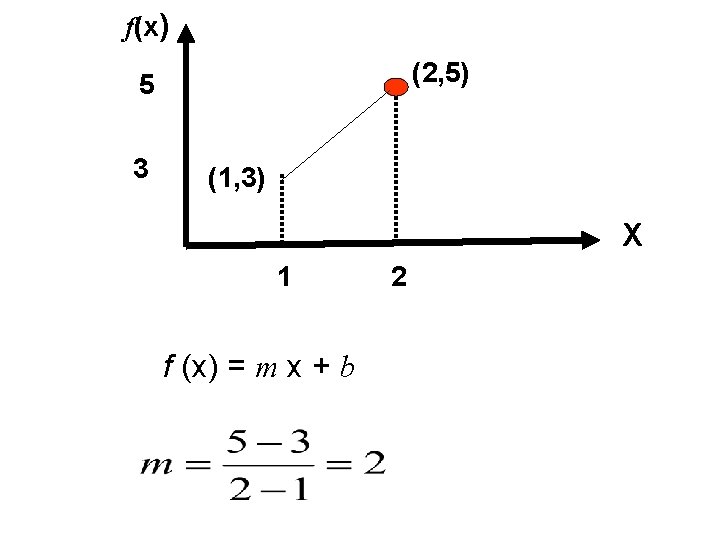
f(x) (2, 5) 5 3 (1, 3) X 1 f (x) = m x + b 2

Z (x, y, z) c (0, 0, 0) X b a Y