Image Restoration Spatial Filtering By Dr Rajeev Srivastava

Image Restoration: Spatial Filtering By Dr. Rajeev Srivastava

Restoration of Noise Only- Spatial Filtering The filters which needs to be considered are: Mean filters • • Arithmetic mean filters Geometric mean filters Harmonic mean filters Contra-harmonic mean filters Order statistics filter • • Median filter Max and min filter Mid point filter Alpha trimmed mean filter

Arithmetic Mean Filter •

Geometric and Harmonic Mean Filter •

Contra-Harmonic Mean Filter •

Classification of Contra-Harmonic Filter Applications The positive order filters effectively reduce the pepper noise, at the expense of blurring the dark areas. The negative order filters effectively reduce the salt noise, at the expense of blurring the bright areas

Arithmetic and geometric mean filters suit the Gaussian or uniform noise Contra harmonic filters suit the impulse noise, yet, with the information of dark or light noise to select the proper file for Q.

Arithmetic and Geometric Mean Filters (Example) 8

Contra-Harmonic Mean Filter (Example) 9

Contra-Harmonic Mean Filter (Example) 10

Order Statistics Filters: Median Filter •

Median Filter (Example) 12

Order Statistics Filters: Max and Min filter Max filter: replace the value of a pixel by the maximum of the grey levels(the brightest points) in the neighborhood of that pixel. Min filter: replace the value of a pixel by the minimum of the gray levels(the darkest points) in the neighborhood of that pixel.

Max and Min Filters (Example) 14

Order Statistics Filters: Midpoint Filter •

Order Statistics Filters: Alpha-Trimmed Mean Filter Output:

The range of ‘d’ lies in between 0 to (mn-1) When d equals 0, it becomes arithmetic mean filter, when it equals ((mn-1)/2), it becomes median filter.

These filters can be used to solve the problem of multi-type noise problem, like combination of salt and pepper noise and Gaussian noise.

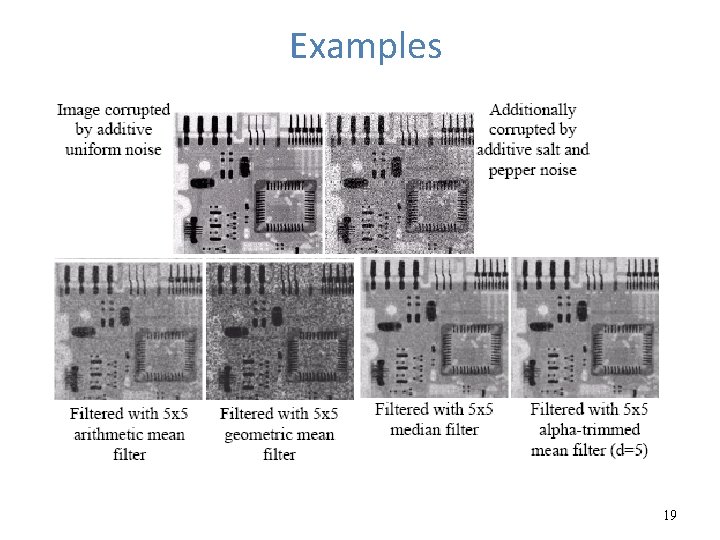
Examples 19

END