Image Reconstruction T61 182 Biomedical Image Analysis Seminar

Image Reconstruction T-61. 182, Biomedical Image Analysis Seminar Presentation 7. 4. 2005 Seppo Mattila & Mika Pollari

Overview • Reconstruction from projections (general) – projection geometry and radon transform • Reconstruction methods – Backprojection, (Fourier slice theorem), Filtered Backprojection, and Algebraic Reconstruction Technique • Reconstruction examples • MRI reconstruction – examples

Introduction • Only photography (reflection) and planar x-ray (attenuation) measure spatial properties of the imaged object directly. • Otherwise, measured parameters are some how related to spatial properties of imaged object. – US (amplitude and time), CT, SPECT and PET (integral projections of parallel rays), MRI (amplitude, frequency and phase of the NMR signal) etc. . . • Construct the object (image) which creates the measured parameters.

Examples CT Scanner CT scanner 1974 GE Pro. Speed Spiral CT

Reconstruction From the Projections • Projection is a line integral along the path: • CT: measure the projections of passed photons, with different angles. • MRI: measure projection of NMR signal with different magnetic gradients (projection based MRI not used anymore). • Assumption: no notable diffraction.

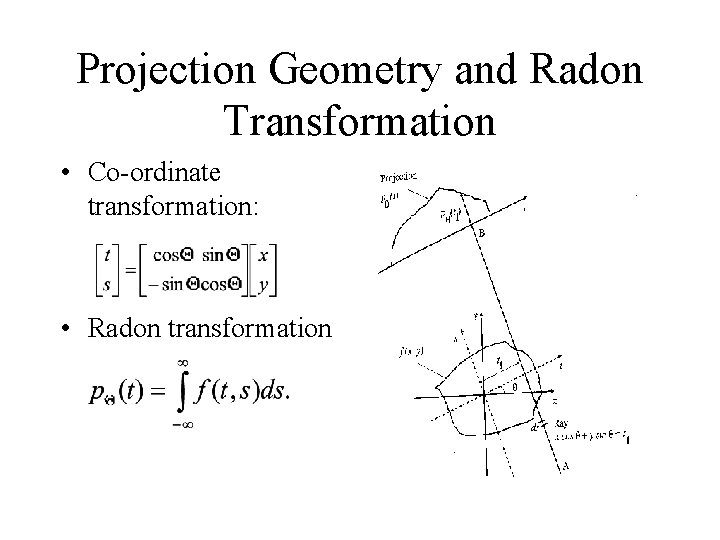
Projection Geometry and Radon Transformation • Co-ordinate transformation: • Radon transformation

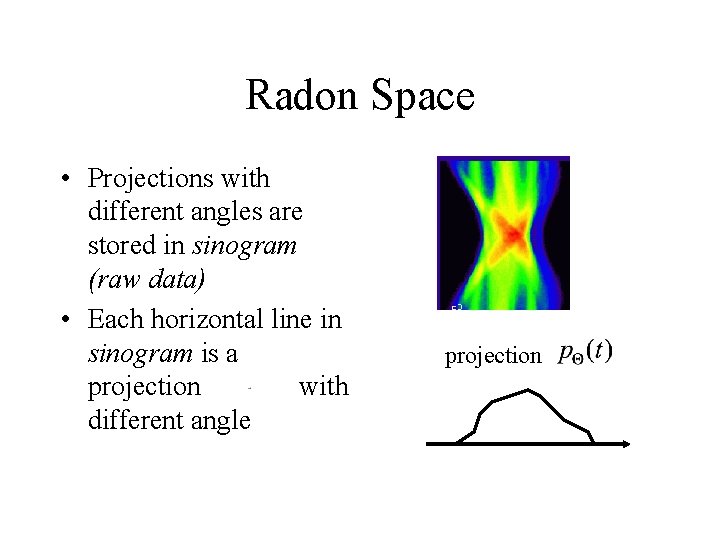
Radon Space • Projections with different angles are stored in sinogram (raw data) • Each horizontal line in sinogram is a projection with different angle projection

Backprojection (BP) • Simplest reconstruction method: Integrate all possible rays that pass through the same point. • Cause smearing and blurring. Method has nowadays only historical importance.

Backprojection Graphically

Point Spread Function (PSF) of BP • Reconstructed image is convolution of the real image and the PSF • PSF cause blurring of the edges and straight lines - solution filtered back projection (later)

Fourier Slice Theorem (FST) • Fourier slice theorem relates three spaces: image, Fourier, and Radon (projection) together.

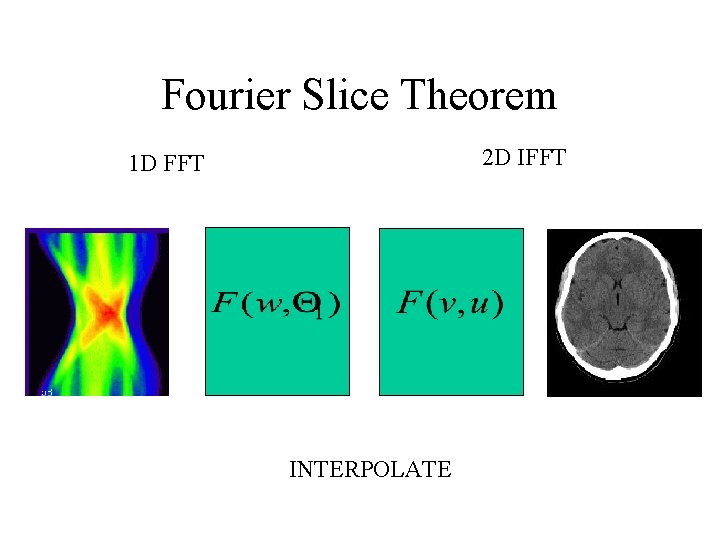
Fourier Slice Theorem 2 D IFFT 1 D FFT INTERPOLATE

Filtered Backprojection (FBP) • Image reconstruction based on FST is computationally inefficient: computation time and memory consumption • FBP utilize FST but is much more efficient

FBP ramp vs. smooth filter

FST and FBP • Starting from FST we end up to FBP without any approximations or assumptions

Remarks of FBP • From the previous equations it’s clear that the image is backprojection of filtered signal ( ) and (|w|) is the ramp filter. • FBP advantages: – Each projection may be filtered and backprojected while further projections are collected (on-line processing). – No need for 2 D inverse Fourier transformation.

Algebraic Reconstruction Techniques (ART) • Each object entity (image pixel/voxel) has physical property (grey-level value) such as attenuation coefficient • All pixel in the rays path contribute to sum an amount which equals pixel’s area along the path (weight) times pixels physical property (grey-level value) • We end up set of simultaneous equations

ART Model • Each ray sum: • Set of simultaneous equations

Kaczmarz Method – Solution to ART • Each equation spans a hyperplane in ndimensional space. If unique solution exist it is in intersection of the hyperplanes • Solution is found iteratively by solving each ray equation at the time

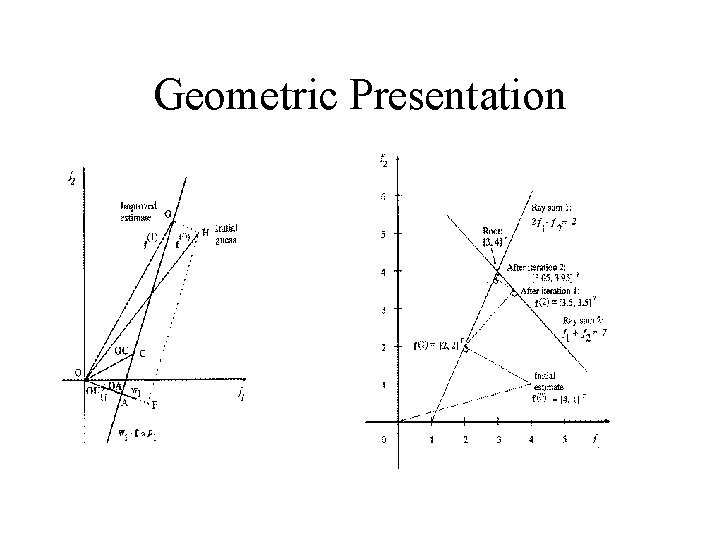
Geometric Presentation

Reconstruction Examples – Number of Projection

Reconstruction Examples – Projection Angle PSF BP FBP (Butter) ART

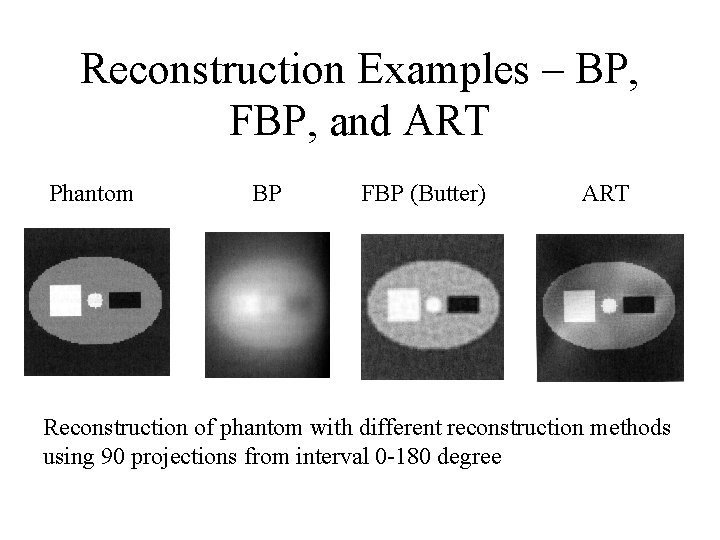
Reconstruction Examples – BP, FBP, and ART Phantom BP FBP (Butter) ART Reconstruction of phantom with different reconstruction methods using 90 projections from interval 0 -180 degree

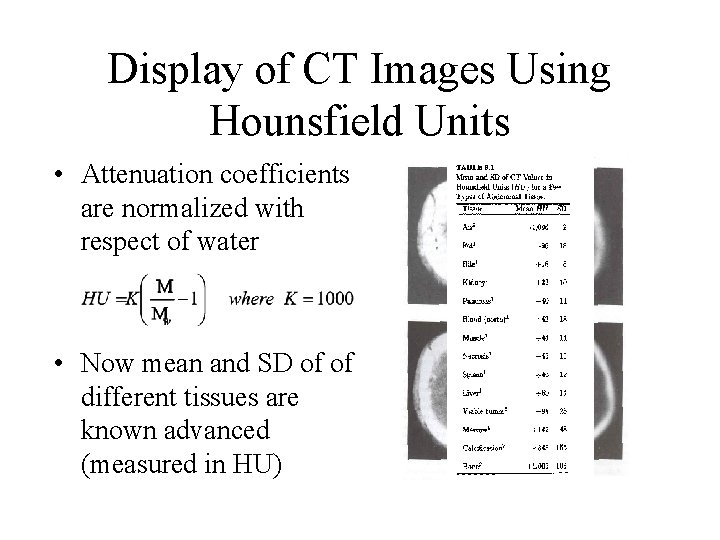
Display of CT Images Using Hounsfield Units • Attenuation coefficients are normalized with respect of water • Now mean and SD of of different tissues are known advanced (measured in HU)

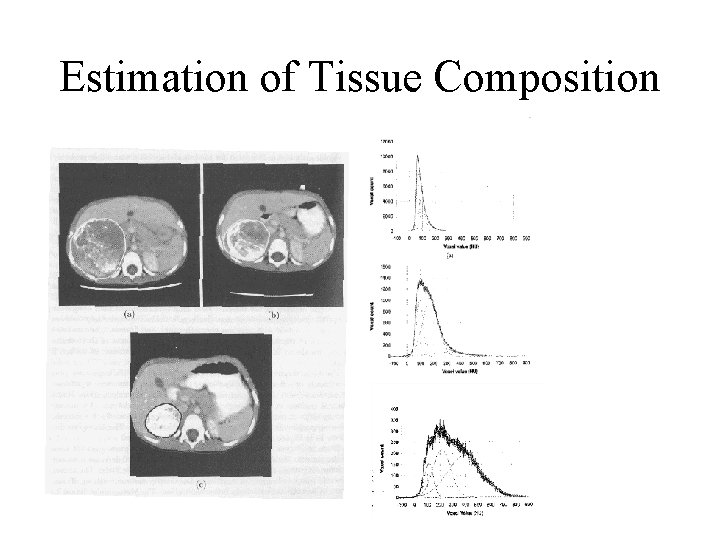
Estimation of Tissue Composition

MRI Reconstruction

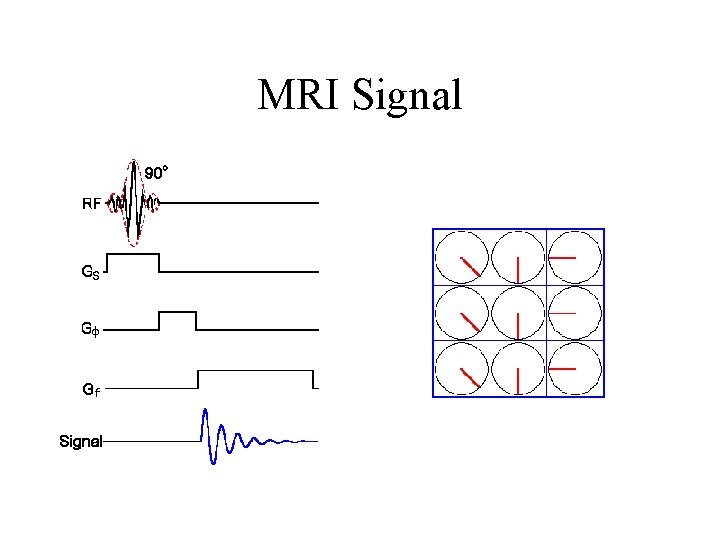
MRI Signal

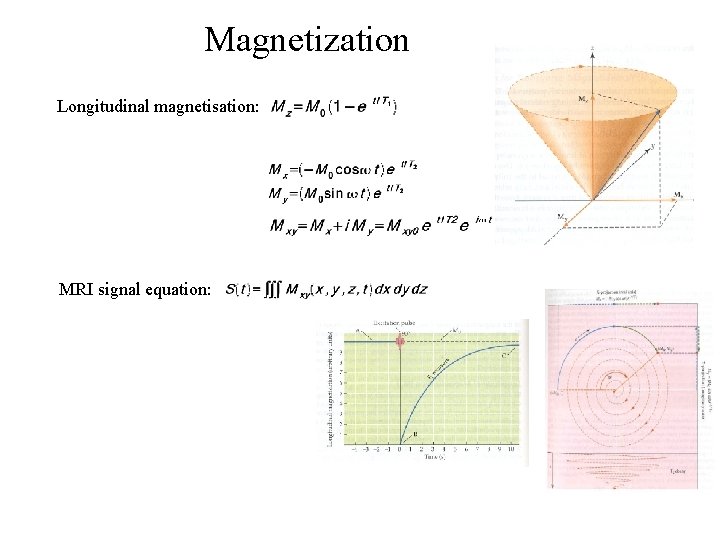
Magnetization Longitudinal magnetisation: MRI signal equation:

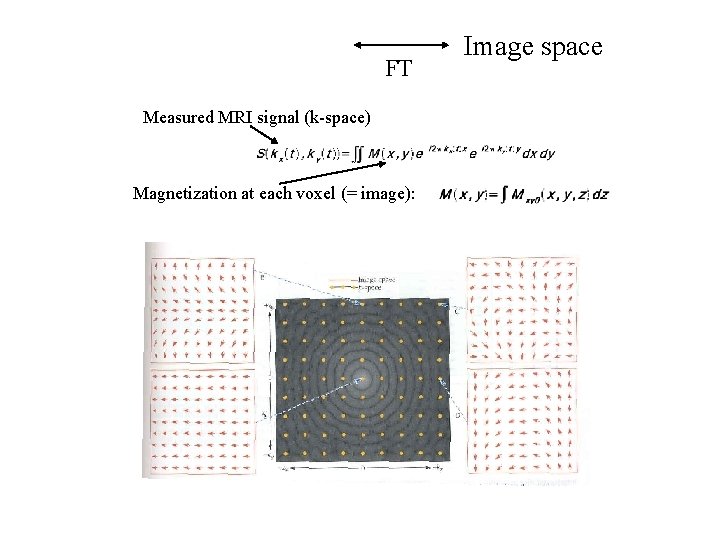
FT Measured MRI signal (k-space) Magnetization at each voxel (= image): Image space

Reconstruction Examples

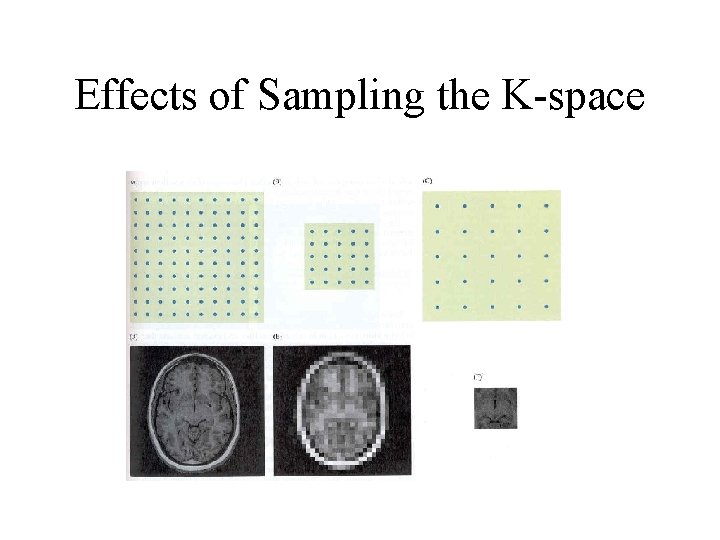
Effects of Sampling the K-space

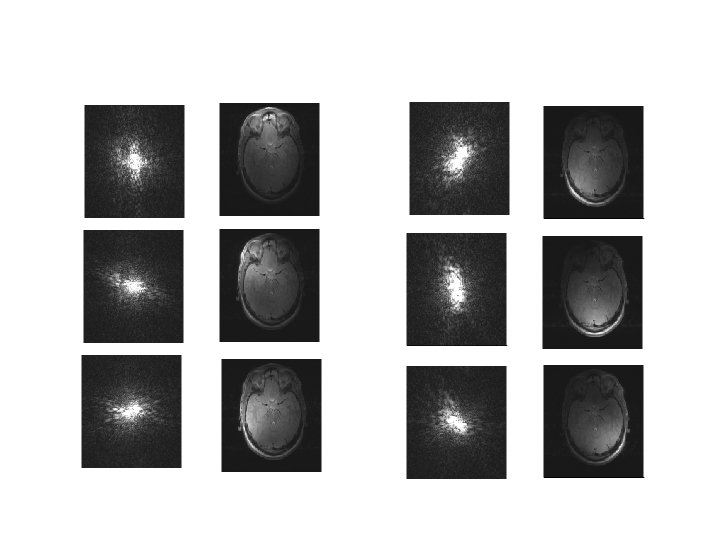
anatomical functional

Summary I Reconstruct 2 D CT image from 1 D projections: • Backprojection (BP) - Only historical importance • Filtered backprojection (FBP) - Most widely used technique - Large number of projections over 0 -180° required • Algebraic Reconstruction Techniques (ART) - Better handling of sparse and non-uniform projections - Slow compared to FBP

Summary II • Reconstruct 2 D MR image from measured current (1 D) • Spatial (x, y) info encoded in frequency and phase • Collect data to spatial frequency domain (k-space) • Reconstruction by inverse 2 D FT + non-invasive + imaging sequences (T 1, T 2, f. MRi etc. ) lots of possibilities - image artifacts (distortions, ghosts, etc. ) - more expensive