Image Processing Targil 2 Image enhancement and edge

Image Processing Targil 2: Image enhancement and edge detection In both cases: using image derivatives

Image Processing Today’s Outline • • 2 Convolution – 1 D, 2 D Image derivatives Sharpening Edge detection

Image Processing Reminder : Convolution (1 D( For example: means that (We do not assume circularity!) 3

Image Processing Properties of Convolution • Commutative • Associative • Distrbutive • Convolution is a linear operator (equivalent to multiplication by a matrix) 4

Image Processing Reminder : Convolution (2 D( image Kernel, Convolver For example: means that 5

Image Processing Application: Spatial filtering Mechanism of spatial filtering 6

Image Processing Smoothening Spatial Filtering 1/9* 1/16* 7 1 1 1 1 1 2 1 2 4 2 1

Image Processing Smoothening Spatial Filtering Using larger filter 8

Image Processing Repeated Convolutios • f * (1 1) = f *? (1 2 1) • f * (1 1) * (1 -1) = f *? (1 0 -1) = f *? (1 2 1)T • f * (1 1) * (1 -1)T = f *? (1 0 -1)T 9 (We do not assume circularity!)

Image Processing An Approximation to Derivatives Implement: convolution with 10

Image Processing An Approximation to Derivatives Implement: convolution with 11

Image Processing An Approximation to Derivatives Implement: convolution with 12

Image Processing An Approximation to Derivatives Second derivative Implement : convolution with Check that: 13

Image Processing Numeric Example – derivative 14

Image Processing Image derivatives (cont(’ Problem: the image is not continuous. A better approximation: • Locally approximate the image with a smooth surface. • Compute the derivatives of this surface. 15

Image Processing Image derivatives (cont(’ Popular kernels (Sobel): • The idea: smooth in one direction, and derivate the orthogonal direction • Note: = 16

Image Processing Image enhancement • Histogram enhancement (histogram equalization…) • Reducing noise (smoothing, median) • Sharpening 17 • Emphasize the details • Make the edges stronger • Problem: we magnify the noise

Image Processing The Laplacian Equation: The matrix: Subtracting the Laplacian: 18

Image Processing Subtracting The Laplacian 19

Image Processing Sharpening Example 20

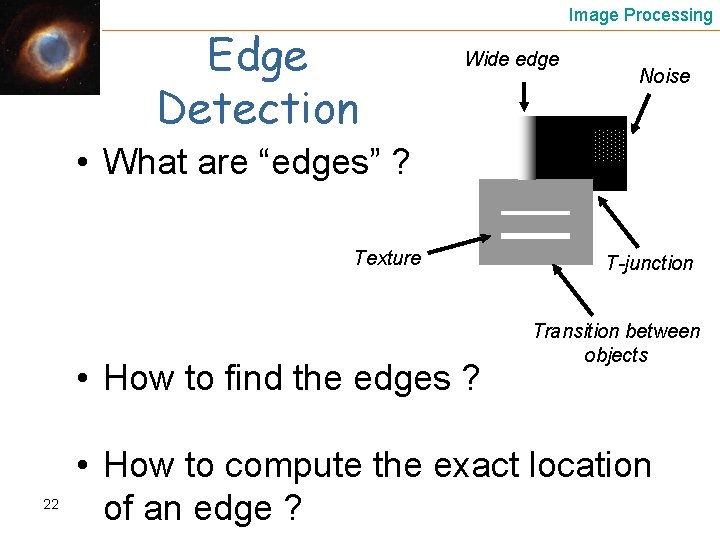
Image Processing Edge Detection Why do we need it ? • A compact representation of the image • More robust to light changes. • Easier to follow (tracking and computations of camera motion) • Segmentation: usually, edges are located at transitions between objects 21 • Used for texture analysis

Edge Detection Image Processing Wide edge Noise • What are “edges” ? Texture • How to find the edges ? 22 T-junction Transition between objects • How to compute the exact location of an edge ?

Image Processing Edges in a picture 23

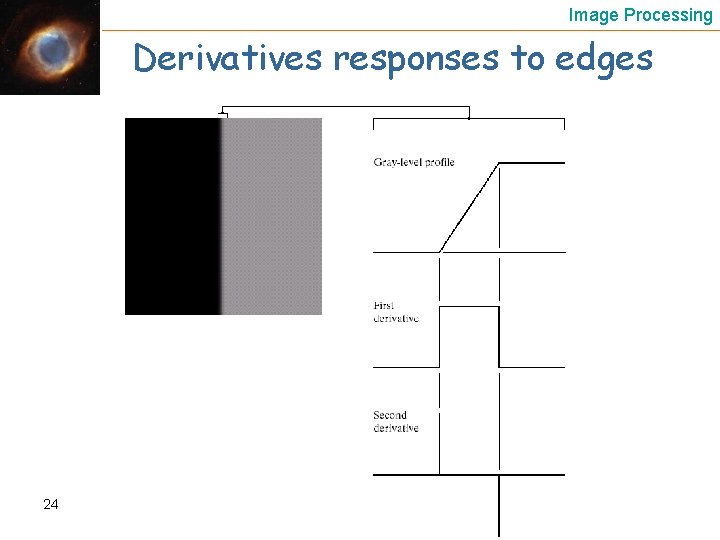
Image Processing Derivatives responses to edges 24

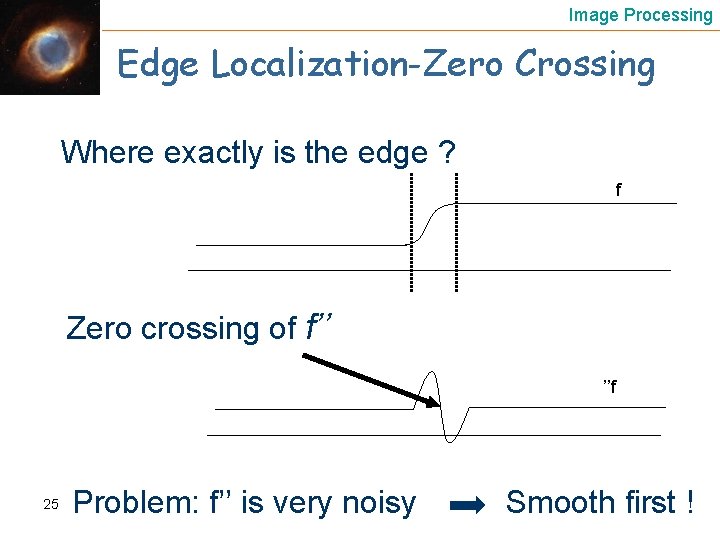
Image Processing Edge Localization-Zero Crossing Where exactly is the edge ? f Zero crossing of f’’ ’’f 25 Problem: f’’ is very noisy Smooth first !

Image Processing Real edges in pictures f 26 f’ f’’

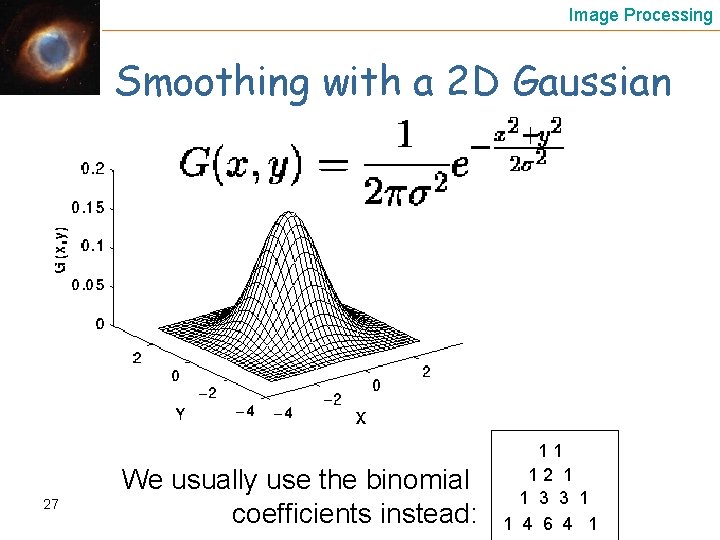
Image Processing Smoothing with a 2 D Gaussian 27 We usually use the binomial coefficients instead: 11 12 1 1 3 3 1 1 4 6 4 1

Image Processing Zero Crossing: Smoothing Example 28

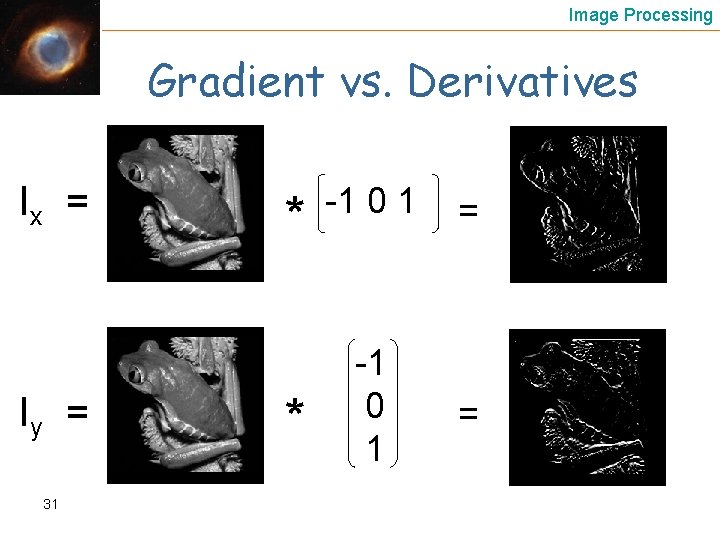
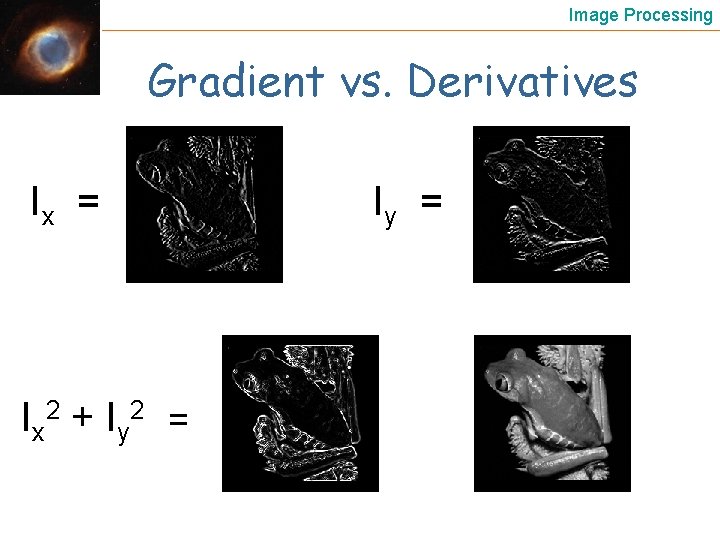
Image Processing The gradient The vector of derivatives The gradient points in the direction of most rapid change in intensity Edge Size Edge Direction 29 Derivative in Direction

Image Processing The gradient Original 30 Gradient

Image Processing Gradient vs. Derivatives Ix = Iy = 31 * -1 0 1 =

Image Processing Gradient vs. Derivatives Ix = Ix 2 + Iy 2 = Iy =

Image Processing Canny Edge Detection • Computing the image derivatives Gx, Gy – Smoothing with a Gaussian. – Using simple derivative kernels. • Compute the edge direction: • Take only the local maxima in that direction (to get an edge with width 1) • Hysteresis: Edge linking with two thresholds • Q. : What will be the width of the Gaussian? 33

Original 34 Example Image Processing Canny