Image Processing Point Processing Filters Dithering Image Compositing

Image Processing Point Processing Filters Dithering Image Compositing Image Compression

Images • Image stored in memory as 2 D pixel array • Value of each pixel controls color • Depth of image is information per pixel – 1 bit: black and white display – 8 bit: 256 colors at any given time via colormap – 16 bit: 5, 6, 5 bits (R, G, B), 216 = 65, 536 colors – 24 bit: 8, 8, 8 bits (R, G, B), 224 = 16, 777, 216 colors

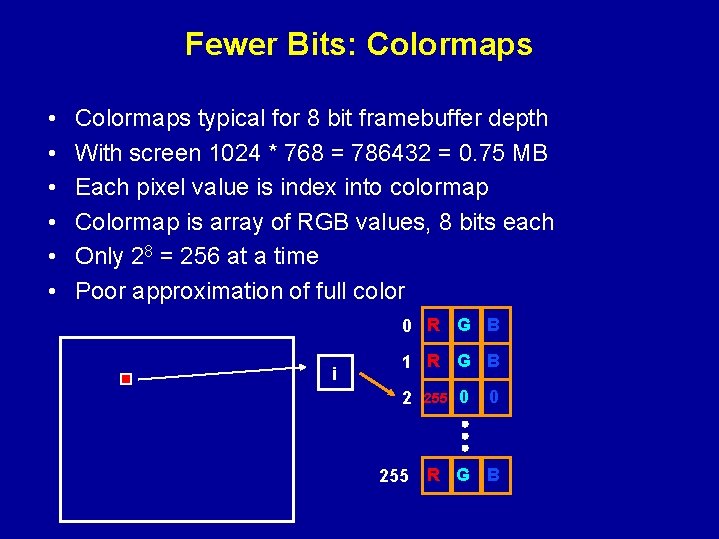
Fewer Bits: Colormaps • • • Colormaps typical for 8 bit framebuffer depth With screen 1024 * 768 = 786432 = 0. 75 MB Each pixel value is index into colormap Colormap is array of RGB values, 8 bits each Only 28 = 256 at a time Poor approximation of full color 0 R G B i 1 R G B 2 255 0 0 255 R G B

Image Processing • • 2 D generalization of signal processing Image as a two-dimensional signal Point processing: modify pixels independently Filtering: modify based on neighborhood Compositing: combine several images Image compression: space-efficient formats Related topics (not in this lecture or this course) – Image enhancement and restoration – Computer vision

Outline • Point Processing • Filters • Dithering • Image Compositing • Image Compression

Point Processing • Input: a[x, y], Output b[x, y] = f(a[x, y]) • f transforms each pixel value separately • Useful for contrast adjustment Suppose our picture is grayscale (a. k. a. monochrome). Let v denote pixel value, suppose it’s in the range [0, 1]. f(v) = v identity; no change f(v) = 1 -v negate an image (black to white, white to black) f(v) = vp, p<1 brighten f(v) = vp, p>1 darken v

Point Processing f(v) = v identity; no change f(v) = 1 -v negate an image (black to white, white to black) f(v) = vp, p<1 brighten f(v) = vp, p>1 darken v

Gamma correction compensates for different monitors Monitors have a intensity to voltage response curve which is roughly a 2. 5 power function Send v actually display a pixel which has intensity equal to v 2. 5 G = 1. 0; f(v) = v G = 2. 5; f(v) = v 1/2. 5 = v 0. 4

Outline • Point Processing • Filters • Dithering • Image Compositing • Image Compression

Signals and Filtering • Audio recording is 1 D signal: amplitude(t) • Image is a 2 D signal: color(x, y) • Signals can be continuous or discrete • Raster images are discrete – In space: sampled in x, y – In color: quantized in value • Filtering: a mapping from signal to signal

Convolution • Used for filtering, sampling and reconstruction • Convolution in 1 D Chalkboard

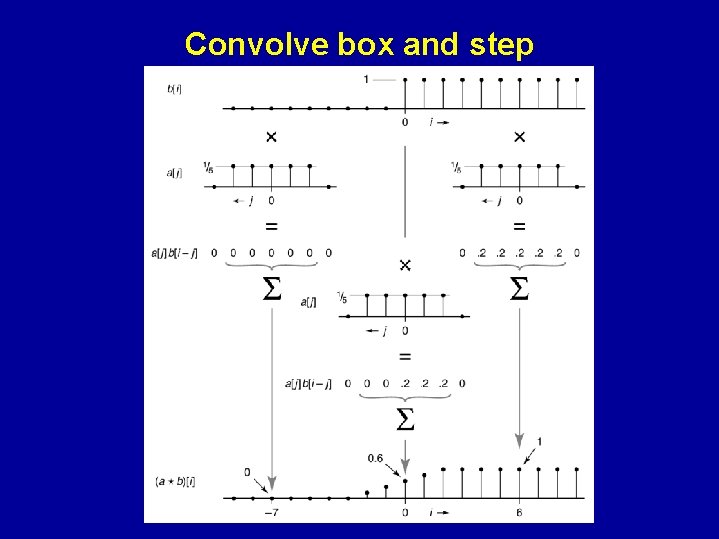
Convolve box and step

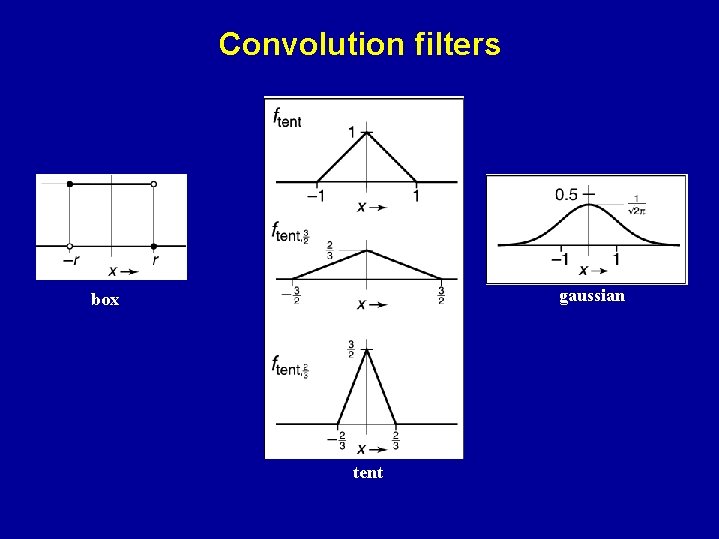
Convolution filters gaussian box tent

Convolution filters • Convolution in 1 D – a(t) is input signal – b(s) is output signal – h(u) is filter • Convolution in 2 D

Filters with Finite Support • Filter h(u, v) is 0 except in given region • Represent h in form of a matrix • Example: 3 x 3 blurring filter • As function • In matrix form

Blurring Filters • A simple blurring effect can be achieved with a 3 x 3 filter centered around a pixel, • More blurring is achieved with a wider n n filter: Original Image Blur 3 x 3 mask Blur 7 x 7 mask

Image Filtering: Blurring original, 64 x 64 pixels 3 x 3 blur 5 x 5 blur

Blurring Filters • Average values of surrounding pixels • Can be used for anti-aliasing • What do we do at the edges and corners? • For noise reduction, use median, not average – Eliminates intensity spikes – Non-linear filter

Example: Noise Reduction Image with noise Median filter (5 x 5)

Example: Noise Reduction Original image Image with noise Median filter (5 x 5)

Edge Filters • Discover edges in image • Characterized by large gradient • Approximate square root • Approximate partial derivatives, e. g. Filter =

Sobel Filter • Edge detection filter, with some smoothing • Approximate • Sobel filter is non-linear – Square and square root (more exact computation) – Absolute value (faster computation)

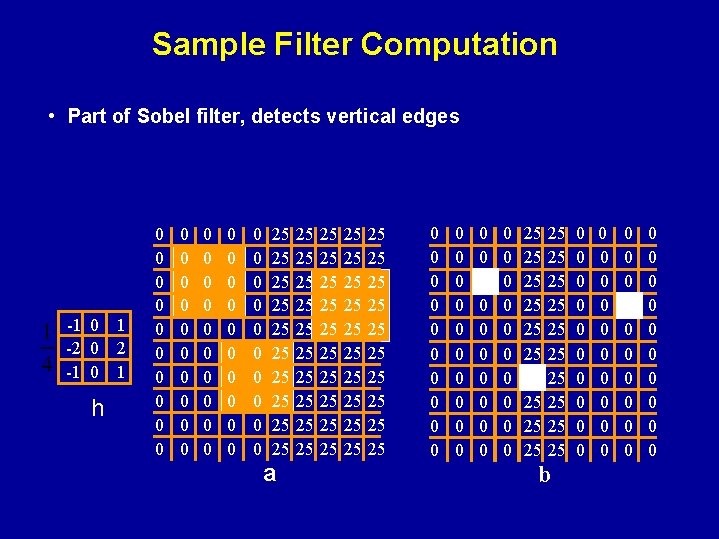
Sample Filter Computation • Part of Sobel filter, detects vertical edges -1 0 1 -2 0 2 -1 0 1 h 0 0 0 0 0 0 0 0 0 0 0 0 0 25 25 25 a 25 25 25 25 25 25 25 25 25 25 0 0 0 0 0 0 0 0 0 0 25 25 25 25 25 b 0 0 0 0 0 0 0 0 0 0

Example of Edge Filter Original image Edge filter, then brightened

Image Filtering: Edge Detection

Outline • Display Color Models • Filters • Dithering • Image Compositing • Image Compression

Dithering • Compensates for lack of color resolution • Eye does spatial averaging • Black/white dithering to achieve gray scale – Each pixel is black or white – From far away, color determined by fraction of white – For 3 x 3 block, 10 levels of gray scale

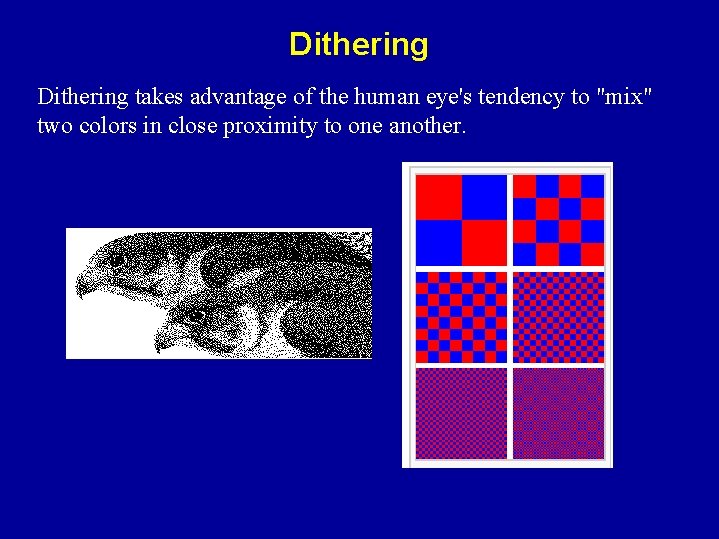
Dithering takes advantage of the human eye's tendency to "mix" two colors in close proximity to one another.

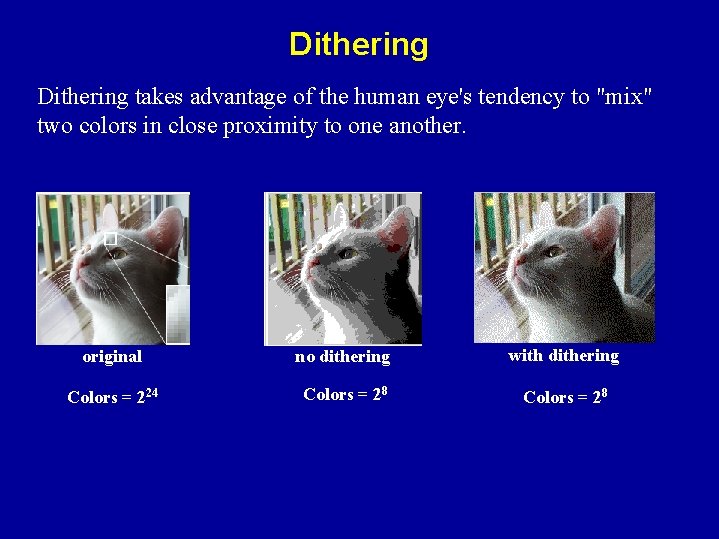
Dithering takes advantage of the human eye's tendency to "mix" two colors in close proximity to one another. original no dithering with dithering Colors = 224 Colors = 28

Ordered Dithering • How do we select a good set of patterns? • Regular patterns create some artifacts • Example of good 3 x 3 dithering matrix

Floyd-Steinberg Error Diffusion • • Diffuse the quantization error of a pixel to its neighboring pixels Scan in raster order At each pixel, draw least error output value Add the error fractions into adjacent, unwritten pixels • If a number of pixels have been rounded downwards, it becomes more likely that the next pixel is rounded upwards 7/16 3/16 5/16 1/16

Floyd-Steinberg Error Diffusion

Floyd-Steinberg Error Diffusion Enhances edges Retains high frequency Some checkerboarding From http: //www. cs. rit. edu/~pga/pics 2000/node 1. html

Color Dithering • Example: 8 bit framebuffer – Set color map by dividing 8 bits into 3, 3, 2 for RGB – Blue is deemphasized because we see it less well • Dither RGB separately – Works well with Floyd-Steinberg • Generally looks good

Outline • Display Color Models • Filters • Dithering • Image Compositing • Image Compression

Image Compositing • Represent an image as layers that are composited (matted) together

Image Compositing • To support this, give image an extra alpha channel in addition to R, G, B • Alpha is opacity: 0 if totally transparent, 1 if totally opaque • Alpha is often stored as an 8 bit quantity; usually not displayed. • Mathematically, to composite a 2 over a 1 according to matte b(x, y) = (1 - (x, y)) • a 1(x, y)+ (x, y) • a 2(x, y) = 0 or 1 -- a hard matte, = between 0 and 1 -- a soft matte • Compositing is useful for photo retouching and special effects.

Special Effects: Compositing • • Lighting match Proper layering Contact with the real world Realism (perhaps) • Applications Cel animation Blue-screen matting

Roger Rabbit http: //members. tripod. com/~Willy_Wonka/Theatr. jpg

Special Effects: Green Screen Green screen Second green screen shot Compositing of everything Digital Domain (from http: //www. vfxhq. com/1997/titanic-picssink. html )

Special Effects: Green Screen Green screen Compositing of people with ship model, sky and digital water Digital Domain (from http: //www. vfxhq. com/1997/titanic-picssink. html )

Outline • Display Color Models • Filters • Dithering • Image Compositing • Image Compression

Image Compression • Exploit redundancy – Coding: some pixel values more common – Interpixel: adjacent pixels often similar – Psychovisual: some color differences imperceptible • Distinguish lossy and lossless methods

Image Sizes • 1024*1024 at 24 bits uses 3 MB • Encyclopedia Britannica at 300 pixels/inch and 1 bit/pixes requires 25 gigabytes (25 K pages) • 90 minute movie at 640 x 480, 24 bits per pixels, 24 frames per second requires 120 gigabytes • Applications: HDTV, DVD, satellite image transmission, medial image processing, fax, . . .

Exploiting Coding Redundancy • Not limited to images (text, other digital info) • Exploit nonuniform probabilities of symbols • Entropy as measure of information content – H = -Si Prob(si) log 2 (Prob(si)) – Low entropy non uniform probability – High entropy uniform probability – If source is independent random variable need H bits

Exploiting Coding Redundancy • Idea: – More frequent symbols get shorter code strings – Best with high redundancy (= low entropy) • Common algorithms – Huffman coding – LZW coding (gzip)

Huffman Coding • Codebook is precomputed and static – Use probability of each symbol to assign code – Map symbol to code – Store codebook and code sequence • Precomputation is expensive lossless • What is “symbol” for image compression?

Exploiting Interpixel Redundancy • Neighboring pixels are correlated • Spatial methods for low-noise image – Run-length coding: » Alternate values and run-length » Good if horizontal neighbors are same » Can be 1 D or 2 D (e. g. used in fax standard) » WWWWWWWWWWWWBBBWWWWWWWWBWWWWWWW » 12 W 1 B 12 W 3 B 24 W 1 B 14 W – Quadtrees: » Recursively subdivide until cells are constant color – Region encoding: » Represent boundary curves of color-constant regions lossless

Improving Noise Tolerance • Predictive coding: – Predict next pixel based on prior ones – Output difference to actual • Transform coding – Exploit frequency domain – Example: discrete cosine transform (DCT) – Used in JPEG lossy compression

Discrete Cosine Transform • Used for lossy compression (as in JPEG) –Subdivide image into n x n blocks (n = 8) –Apply discrete cosine transform for each block –Each tile is converted to frequency space

Discrete Cosine Transform • Quantize – Human eye good at seeing variations over large area – Not good at seeing the exact strength of a high frequency – Greatly reducing the amount of information in the high frequency components • Use variable length coding (e. g. Huffman)