Image Processing Math Review Towards Fourier Transform Linear

Image Processing Math Review Towards Fourier Transform • Linear Spaces • Change of Basis • Cosines and Sines • Complex Numbers 1

Part I: Vector Spaces and Basis Vectors 2

Basis Vectors • A given vector value is represented with respect to a coordinate system. • The coordinate system is arbitrarily chosen. • A coordinate system is defined by a set of linearly independent vectors forming the system basis. • Any vector value is represented as a linear sum of the basis vectors. a= 0. 5 *v 1+1*v 2 (0. 5 , 1)v v 1 a • v 1, v 2 are basis vectors • The representation of a with respect to this basis is (0. 5, 1) v 2 3

Orthonormal Basis Vectors • If the basis vectors are mutually orthogonal and are unit vectors, the vectors form an orthonormal basis. • Example: The standard basis is orthonormal: V 1=(1 0 0 0 …) V 2=(0 1 0 0 …) V 3=(0 0 1 0 …) …. V 2=(0 1) a V 1=(1 0) 4

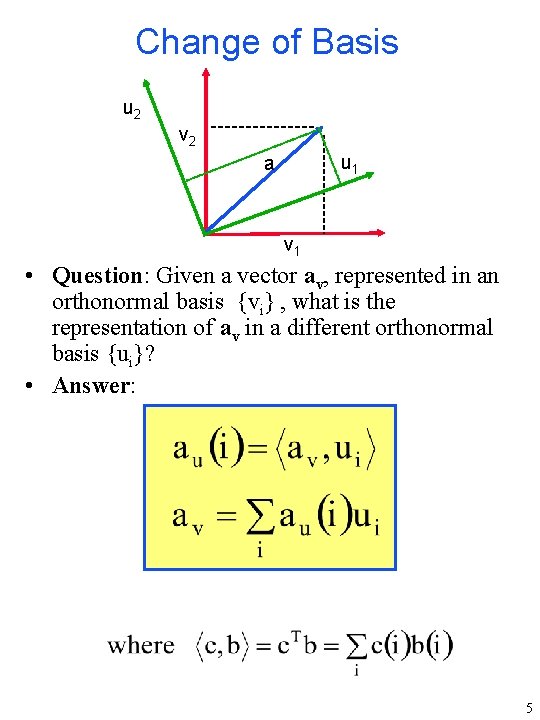
Change of Basis u 2 v 2 u 1 a v 1 • Question: Given a vector av, represented in an orthonormal basis {vi} , what is the representation of av in a different orthonormal basis {ui}? • Answer: 5

Change of Basis: Matrix Form u 2 v 2 u 1 a v 1 • Defining the new basis as a collection of columns in a matrix form 6

Signal (image) Transforms 1. Basis Functions. 2. Method for finding the transform coefficients given a signal. 3. Method for finding the signal given the transform coefficients. 7

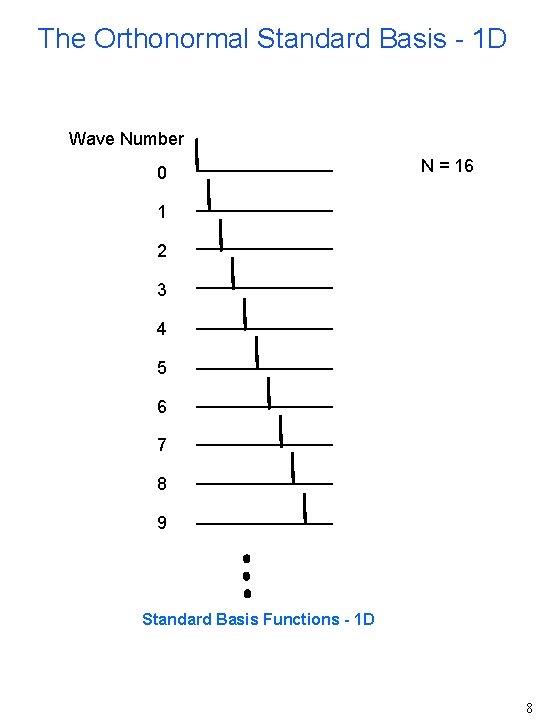
The Orthonormal Standard Basis - 1 D Wave Number 0 N = 16 1 2 3 4 5 6 7 8 9 Standard Basis Functions - 1 D 8

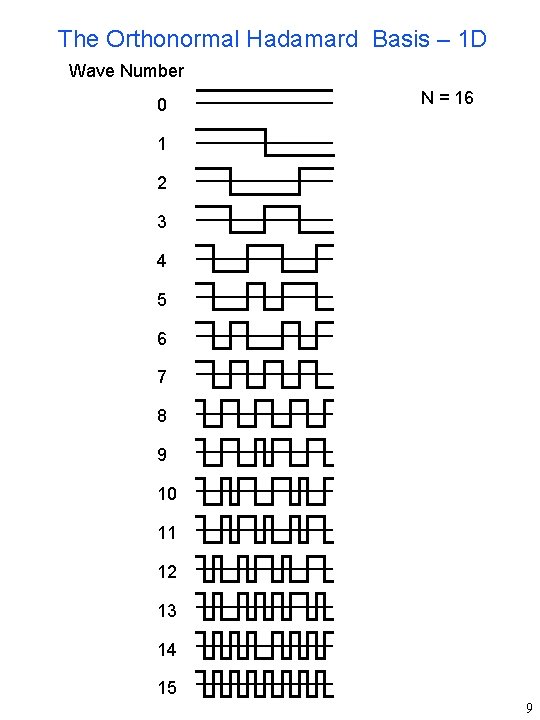
The Orthonormal Hadamard Basis – 1 D Wave Number 0 N = 16 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 9

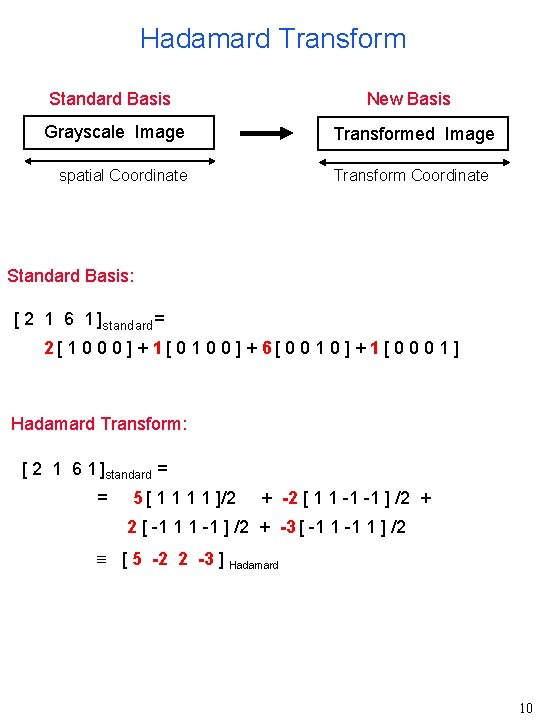
Hadamard Transform Standard Basis New Basis Grayscale Image Transformed Image Transform Coordinate spatial Coordinate Standard Basis: [ 2 1 6 1 ]standard= 2[ 1 0 0 0 ] + 1[ 0 1 0 0 ] + 6[ 0 0 1 0 ] + 1[ 0 0 0 1 ] Hadamard Transform: [ 2 1 6 1 ]standard = = 5 [ 1 1 ]/2 + -2 [ 1 1 -1 -1 ] /2 + 2 [ -1 1 1 -1 ] /2 + -3 [ -1 1 ] /2 [ 5 -2 2 -3 ] Hadamard 10

Finding the transform coefficients Signal: X = [ 2 1 6 1] standard Hadamard Basis: T 0 = [ 1 1 ] /2 T 1 = [ 1 1 -1 -1 ] /2 T 2 = [ -1 1 1 -1 ] /2 T 3 = [ -1 1 ] /2 Hadamard Coefficients: a 0 = <X, T 0 > = < [ 2 1 6 1 ] , [ 1 1 ] > /2 = 5 a 1 = <X, T 1 > = < [ 2 1 6 1 ] , [ 1 1 -1 -1 ] > /2 = -2 a 2 = <X, T 2 > = < [ 2 1 6 1 ] , [ -1 1 1 -1 ] > /2 = 2 a 3 = <X, T 3 > = < [ 2 1 6 1 ] , [ -1 1 ] > /2 = -3 Signal: [ 2 1 6 1] Standard [ 5 -2 2 -3 ] Hadamard 11

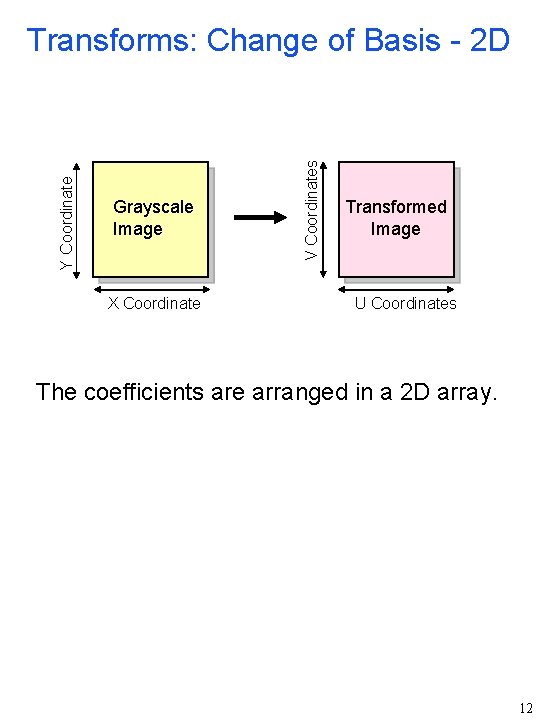
Grayscale Image X Coordinate V Coordinates Y Coordinate Transforms: Change of Basis - 2 D Transformed Image U Coordinates The coefficients are arranged in a 2 D array. 12

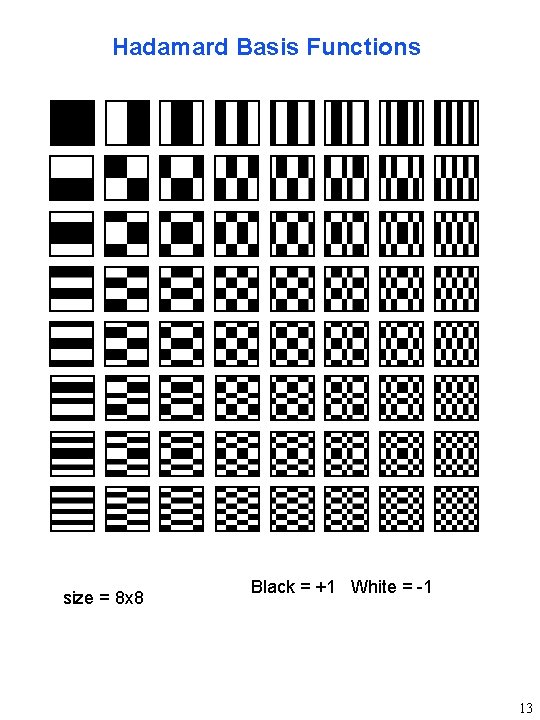
Hadamard Basis Functions size = 8 x 8 Black = +1 White = -1 13

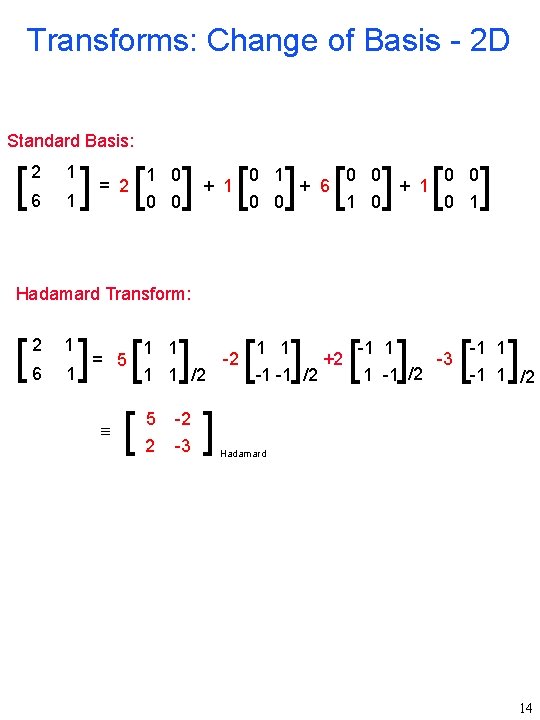
Transforms: Change of Basis - 2 D Standard Basis: [ 2 1 6 1 ] [ ] [ ] = 2 1 0 0 0 + 1 0 0 + 6 0 0 1 0 + 1 0 0 0 1 Hadamard Transform: [ 2 1 6 1 ] [ ] = 5 [ 1 1 /2 5 -2 2 -3 ] -2 [ ] 1 1 -1 -1 /2 +2 -1 1 1 -1 /2 -3 [ ] -1 1 /2 Hadamard 14

Finding the transform coefficients X = Signal: [ 2 1 6 1 ] standard New Basis: [ ]/2 T 11 = T 21 = Signal: 1 1 -1 [ ]/2 T 12 = T 22 = 1 1 -1 -1 -1 1 X = a 11 T 11 +a 12 T 12 + a 21 T 21 + a 22 T 22 New Coefficients: a 11 = a 12 = a 21 = a 22 = <X, T 11 > = <X, T 12 > = <X, T 21 > = <X, T 22 > = X sum(X. *T 11)) = sum(X. *T 12)) = sum(X. *T 21)) = sum(X. *T 22)) = [ 5 -2 2 -3 ] 5 -2 2 -3 new 15

Standard Basis: [ 2 1 6 1 [ ] ] coefficients 1 0 0 0 0 [ ] 0 0 1 Standard Basis Elements Hadamard Transform: [ 5 -2 2 -3 ] coefficients [ ] Hadamard 1 1 1 /2 -1 -1 /2 [ ] -1 1 1 -1 /2 -1 1 /2 Hadamard Basis Elements 16

Part II: Sines and Cosines 17

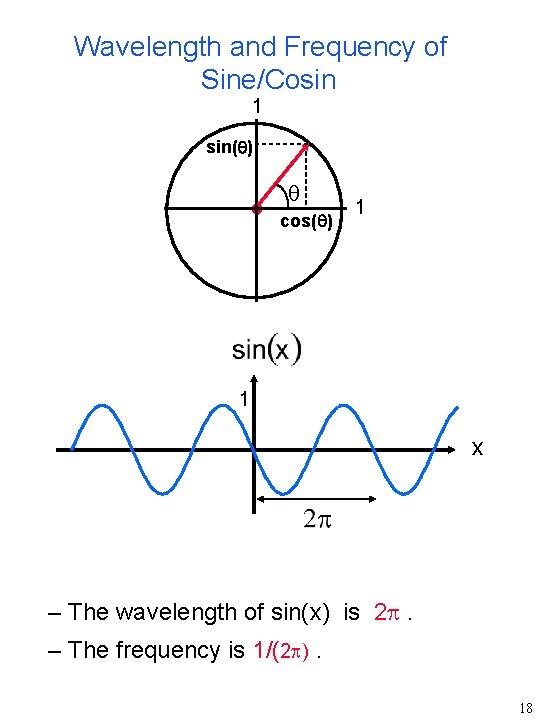
Wavelength and Frequency of Sine/Cosin 1 sin( ) cos( ) 1 1 x – The wavelength of sin(x) is 2 . – The frequency is 1/(2 ). 18

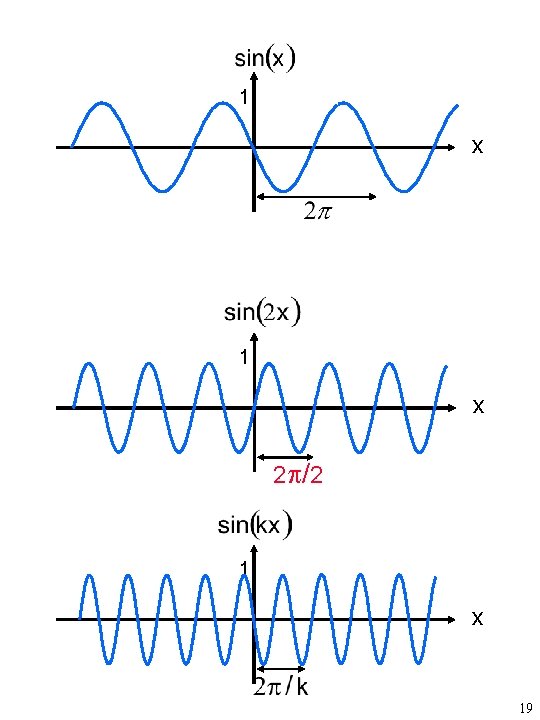
1 x 2 /2 1 x 19

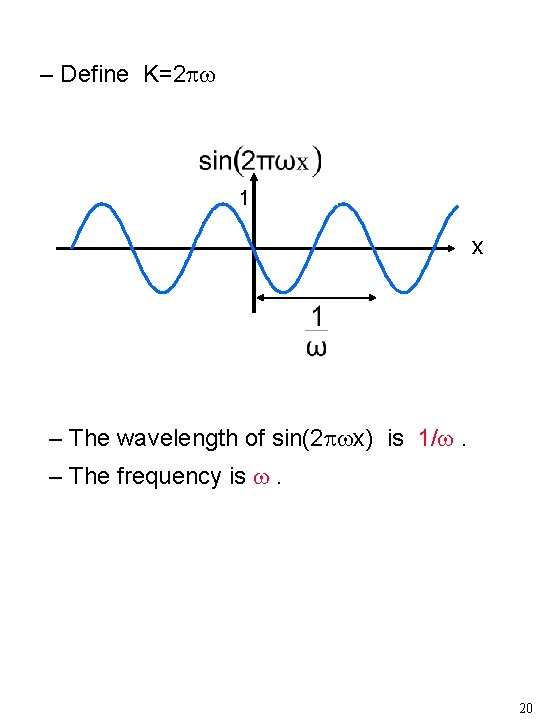
– Define K=2 1 x – The wavelength of sin(2 x) is 1/ . – The frequency is . 20

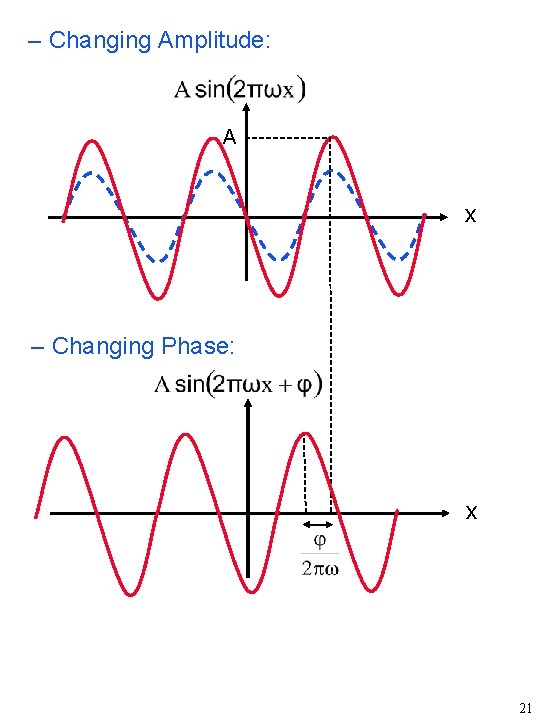
– Changing Amplitude: A x – Changing Phase: x 21

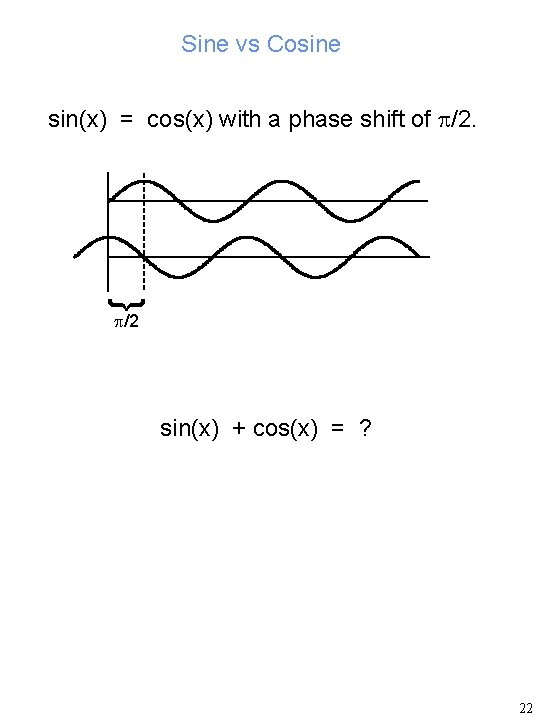
Sine vs Cosine sin(x) = cos(x) with a phase shift of /2. } /2 sin(x) + cos(x) = ? 22

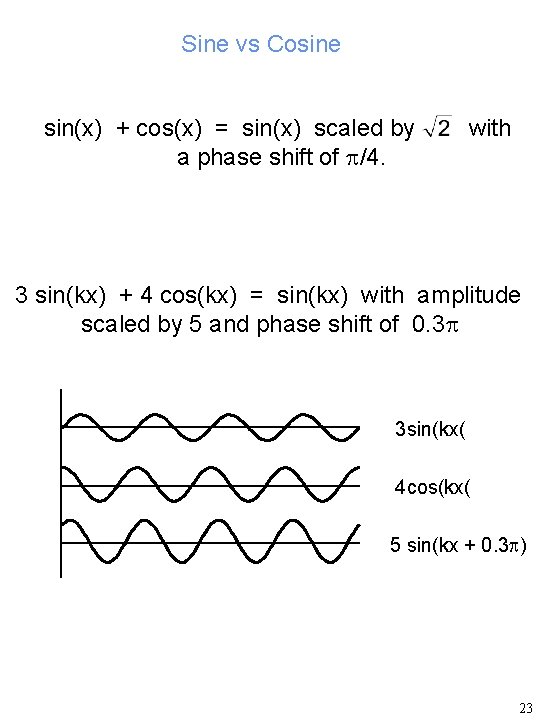
Sine vs Cosine sin(x) + cos(x) = sin(x) scaled by a phase shift of /4. with 3 sin(kx) + 4 cos(kx) = sin(kx) with amplitude scaled by 5 and phase shift of 0. 3 3 sin(kx( 4 cos(kx( 5 sin(kx + 0. 3 ) 23

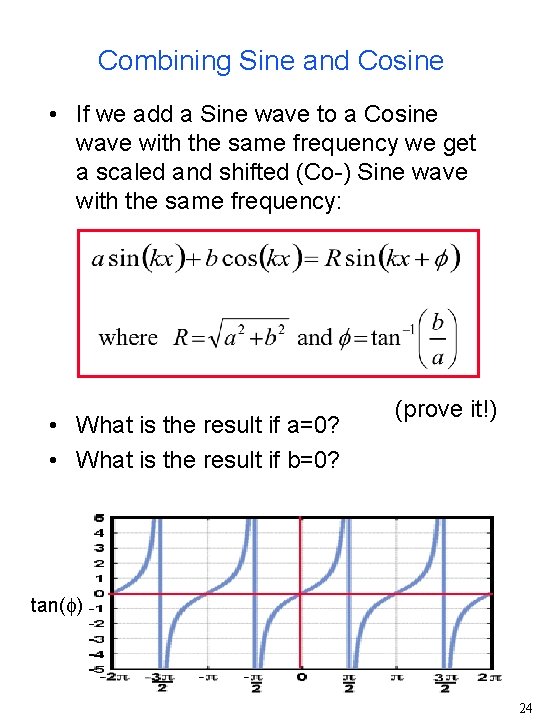
Combining Sine and Cosine • If we add a Sine wave to a Cosine wave with the same frequency we get a scaled and shifted (Co-) Sine wave with the same frequency: • What is the result if a=0? • What is the result if b=0? (prove it!) tan( ) 24

Part III: Complex Numbers 25

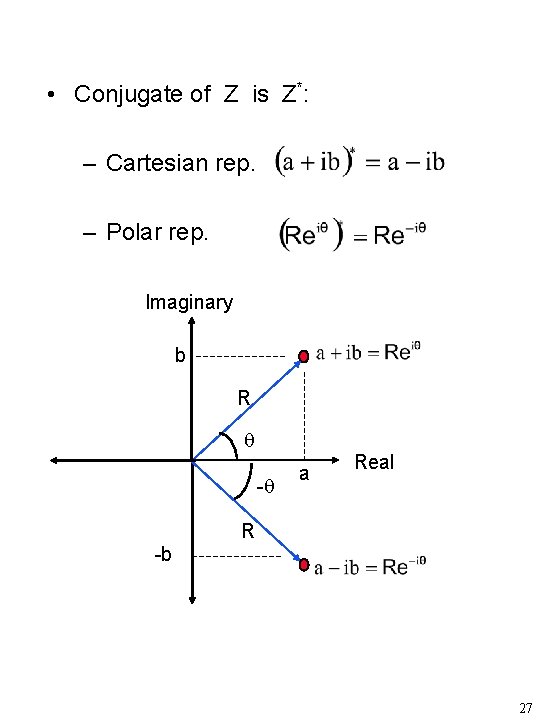
Complex Numbers Imaginary )a, b( b R The Complex Plane a Real • Two kind of representations for a point (a, b) in the complex plane – The Cartesian representation: – The Polar representation: )Complex exponential( • Conversions: – Polar to Cartesian: – Cartesian to Polar 26

• Conjugate of Z is Z*: – Cartesian rep. – Polar rep. Imaginary b R - -b a Real R 27

Algebraic operations: • addition/subtraction: • multiplication: • inner Product: • norm: 28

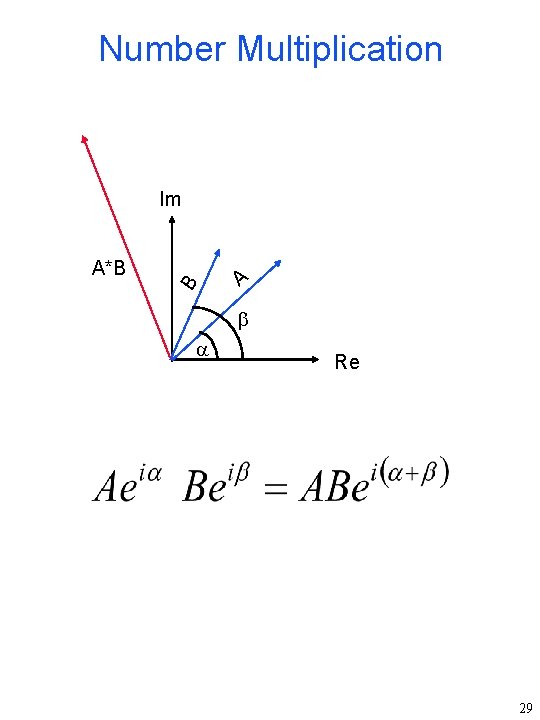
Number Multiplication Im A*B B A Re 29

The (Co-) Sinusoid • The (Co-)Sinusoid as complex exponential: Or • What about generalization? S sin(kx) + C cos(kx) = ? 30

We saw that : S sin(kx) + C cos(kx) = R sin(kx + ) where -1 æ C ö 2 2 = + = R tan çç S C and èS ø Using Complex exponentials: Scaling and phase shifting can be represented as a multiplication with and also 31

THE END 32