Image Processing cgvr korea ac kr Image Processing

Image Processing cgvr. korea. ac. kr

Image Processing • Quantization • • Uniform quantization Random dither Ordered dither Floyd-Steinberg dither n Filtering n n n Warping n n n • Pixel operations • • Add random noise Add luminance Add contrast Add saturation n Blur Detect edge Scale Rotate Warps Combining n n cgvr. korea. ac. kr Morphs Composite

Image Processing • Quantization • • Uniform quantization Random dither Ordered dither Floyd-Steinberg dither n Filtering n n n Warping n n n • Pixel operations • • Add random noise Add luminance Add contrast Add saturation n Blur Detect edge Scale Rotate Warps Combining n n cgvr. korea. ac. kr Morphs Composite

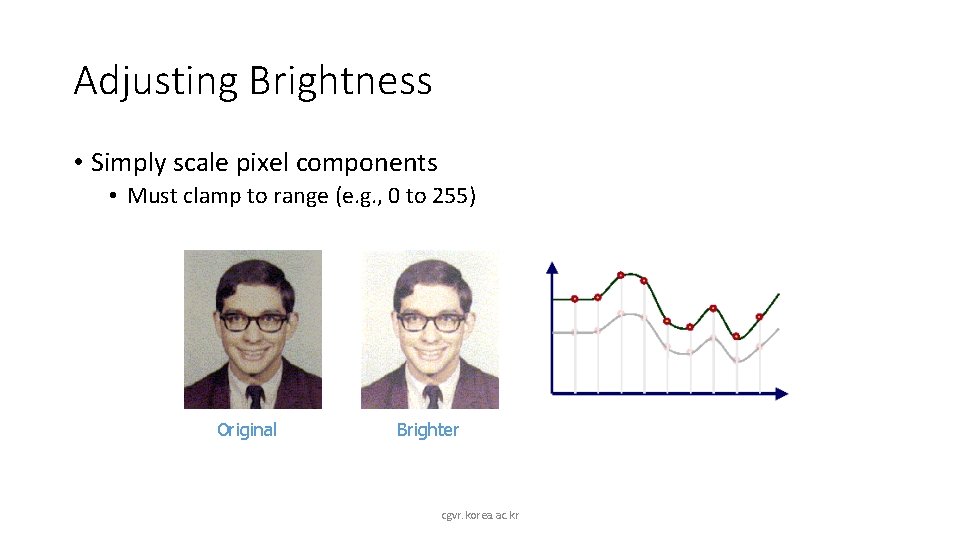
Adjusting Brightness • Simply scale pixel components • Must clamp to range (e. g. , 0 to 255) Original Brighter cgvr. korea. ac. kr

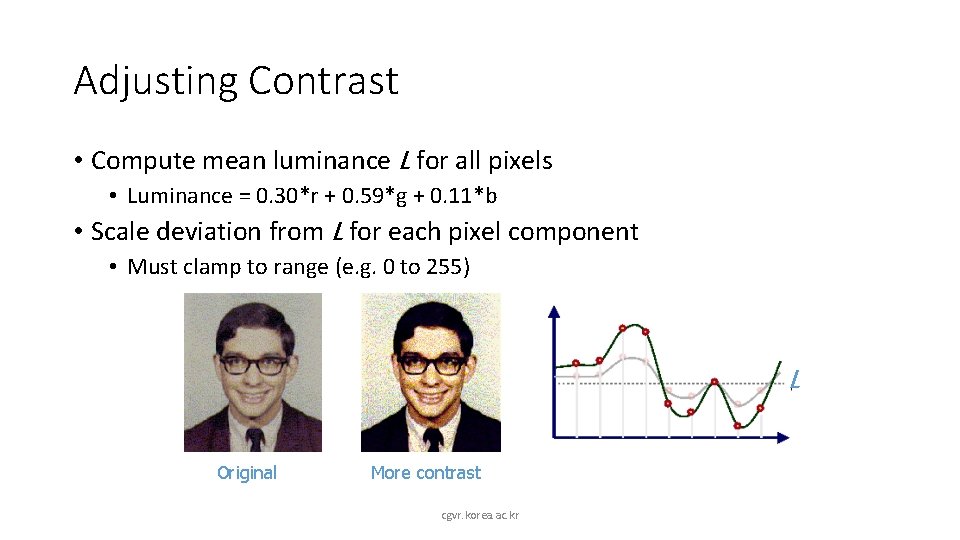
Adjusting Contrast • Compute mean luminance L for all pixels • Luminance = 0. 30*r + 0. 59*g + 0. 11*b • Scale deviation from L for each pixel component • Must clamp to range (e. g. 0 to 255) L Original More contrast cgvr. korea. ac. kr

Image Processing • Quantization • • Uniform quantization Random dither Ordered dither Floyd-Steinberg dither n Filtering n n n Warping n n n • Pixel operations • • Add random noise Add luminance Add contrast Add saturation n Blur Detect edge Scale Rotate Warps Combining n n cgvr. korea. ac. kr Morphs Composite

Adjusting Blurriness • Convolve with a filter whose entries sum to one • Each pixel becomes a weighted average of its neighbors Original Blur cgvr. korea. ac. kr

Edge Detection • Convolve with a filter that finds differences between neighbor pixels Original Edge Detection cgvr. korea. ac. kr

Image Processing • Quantization • • Uniform quantization Random dither Ordered dither Floyd-Steinberg dither n Filtering n n n Warping n n n • Pixel operations • • Add random noise Add luminance Add contrast Add saturation n Blur Detect edge Scale Rotate Warps Combining n n cgvr. korea. ac. kr Morphs Composite

Image Warping • Move pixels of image • Mapping • Resampling Warp Source Image Destination Image cgvr. korea. ac. kr

Overview • Mapping • Forward • Reverse • Resampling • Point sampling • Triangle filter • Gaussian filter cgvr. korea. ac. kr

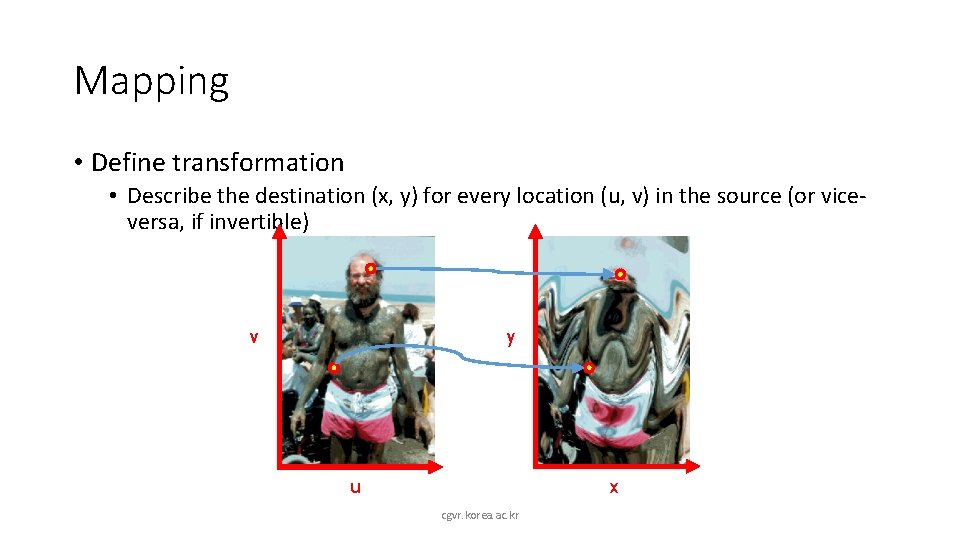
Mapping • Define transformation • Describe the destination (x, y) for every location (u, v) in the source (or viceversa, if invertible) v y u x cgvr. korea. ac. kr

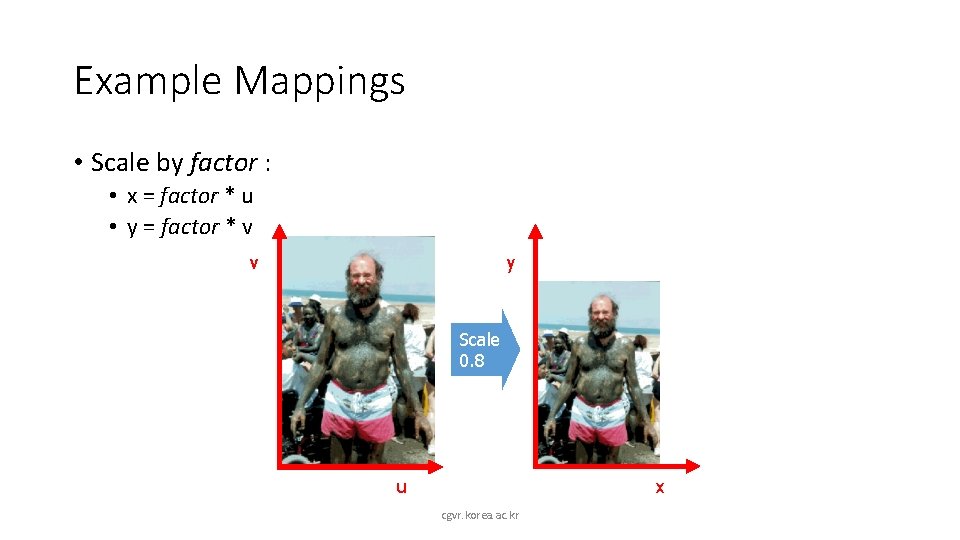
Example Mappings • Scale by factor : • x = factor * u • y = factor * v v y Scale 0. 8 u x cgvr. korea. ac. kr

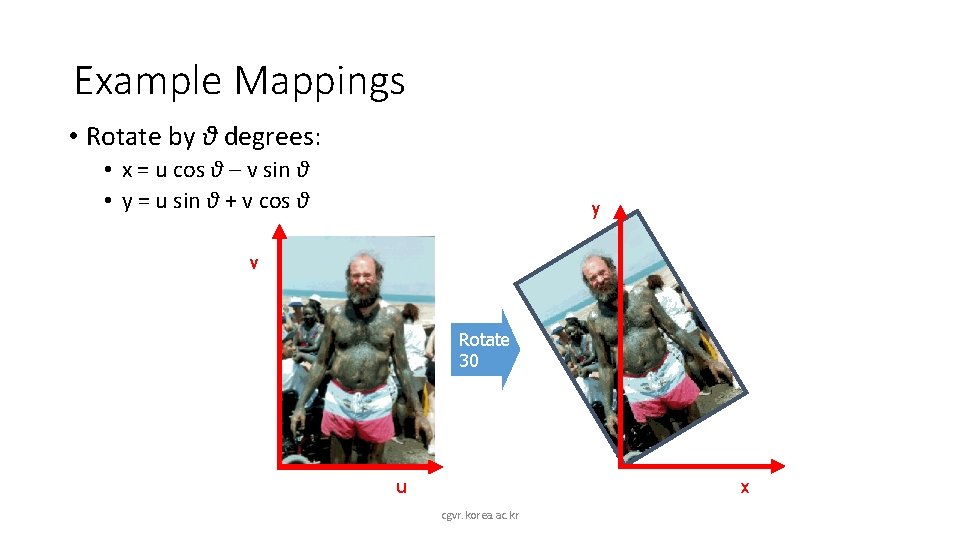
Example Mappings • Rotate by θ degrees: • x = u cos θ – v sin θ • y = u sin θ + v cos θ y v Rotate 30 x u cgvr. korea. ac. kr

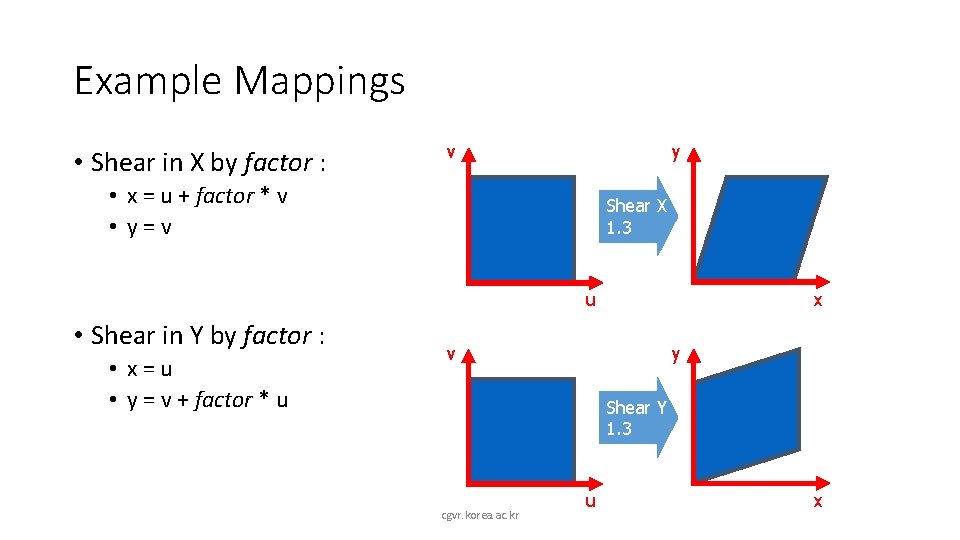
Example Mappings • Shear in X by factor : v y • x = u + factor * v • y=v Shear X 1. 3 u • Shear in Y by factor : • x=u • y = v + factor * u x v y Shear Y 1. 3 cgvr. korea. ac. kr u x

Other Mappings • Any function of u and v : • x = fx(u, v) • y = fy(u, v) Fish-eye Swirl cgvr. korea. ac. kr Rain

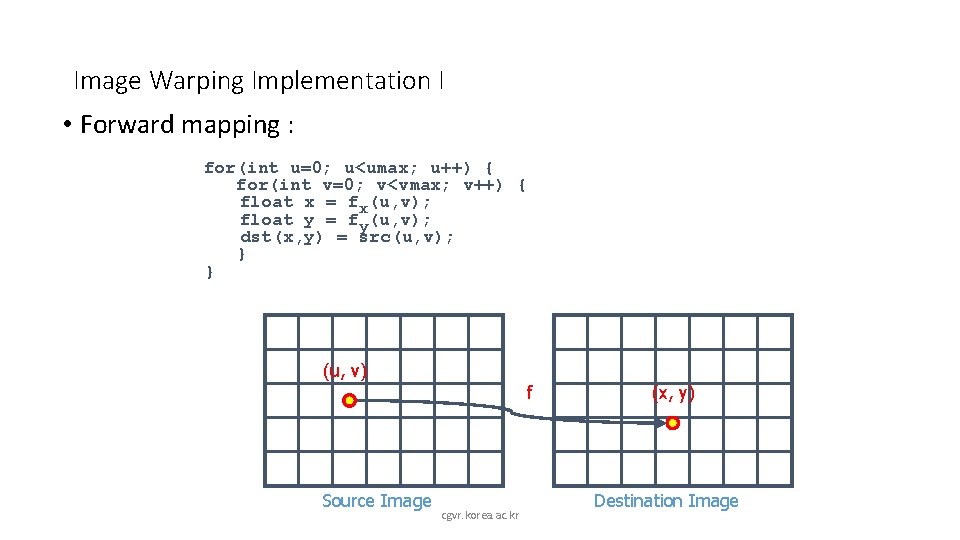
Image Warping Implementation I • Forward mapping : for(int u=0; u<umax; u++) { for(int v=0; v<vmax; v++) { float x = fx(u, v); float y = fy(u, v); dst(x, y) = src(u, v); } } (u, v) f Source Image cgvr. korea. ac. kr (x, y) Destination Image

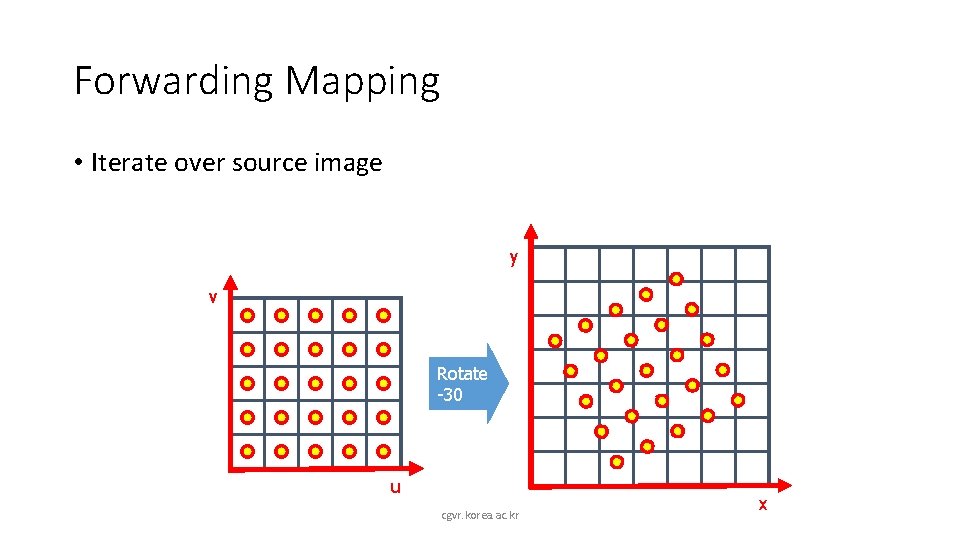
Forwarding Mapping • Iterate over source image y v Rotate -30 u cgvr. korea. ac. kr x

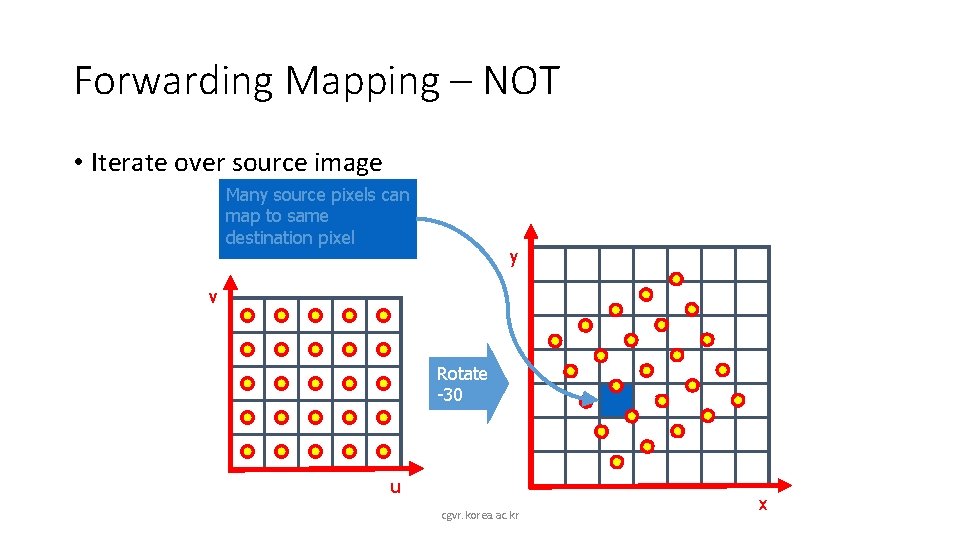
Forwarding Mapping – NOT • Iterate over source image Many source pixels can map to same destination pixel y v Rotate -30 u cgvr. korea. ac. kr x

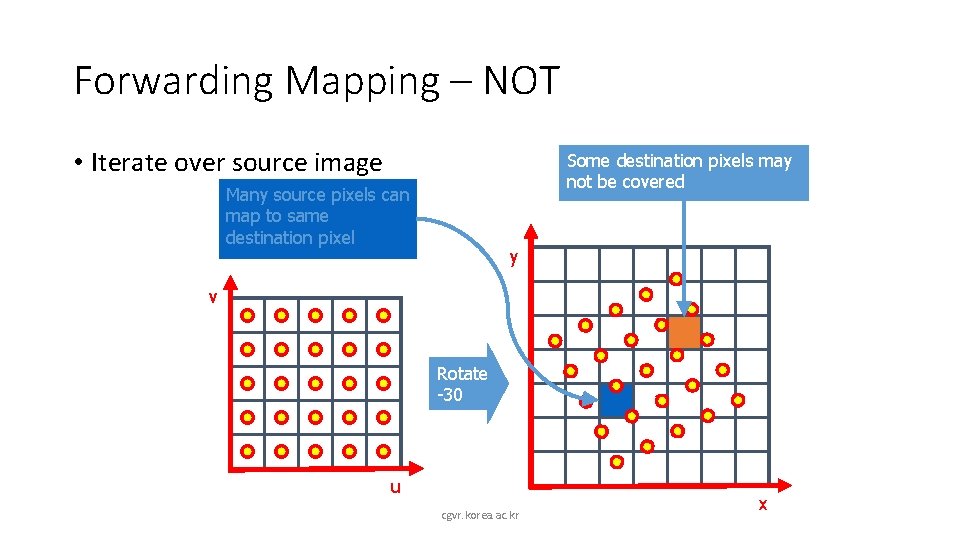
Forwarding Mapping – NOT • Iterate over source image Some destination pixels may not be covered Many source pixels can map to same destination pixel y v Rotate -30 u cgvr. korea. ac. kr x

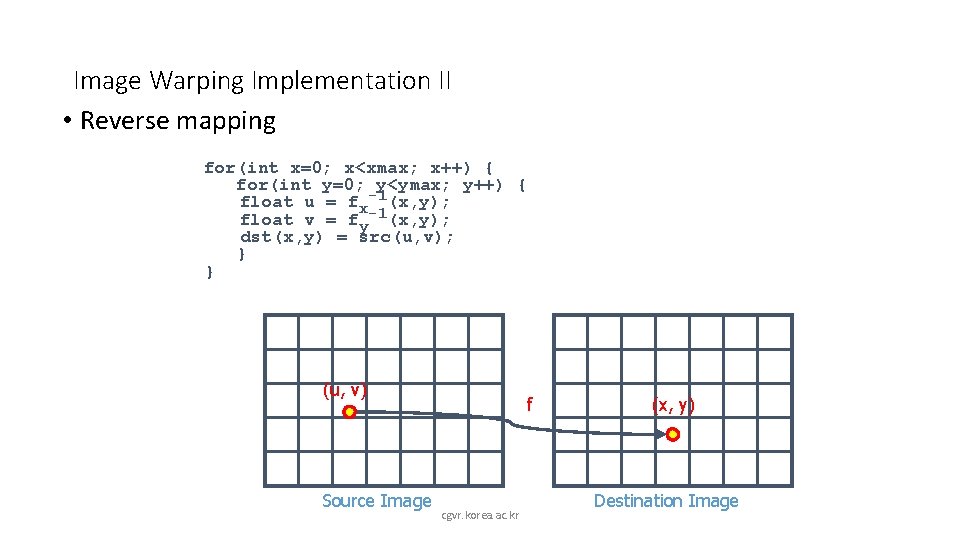
Image Warping Implementation II • Reverse mapping for(int x=0; x<xmax; x++) { for(int y=0; y<ymax; y++) { float u = fx-1(x, y); float v = fy-1(x, y); dst(x, y) = src(u, v); } } (u, v) Source Image f cgvr. korea. ac. kr (x, y) Destination Image

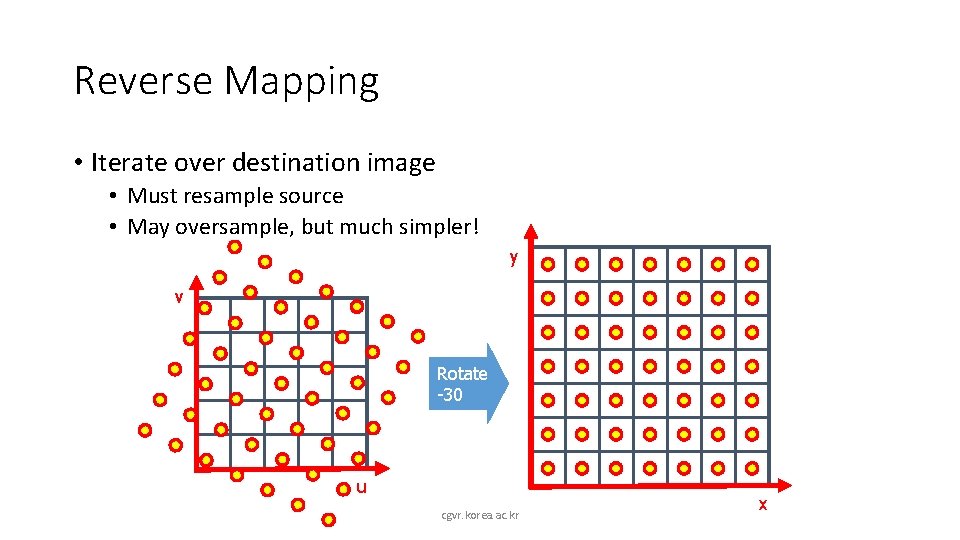
Reverse Mapping • Iterate over destination image • Must resample source • May oversample, but much simpler! y v Rotate -30 u cgvr. korea. ac. kr x

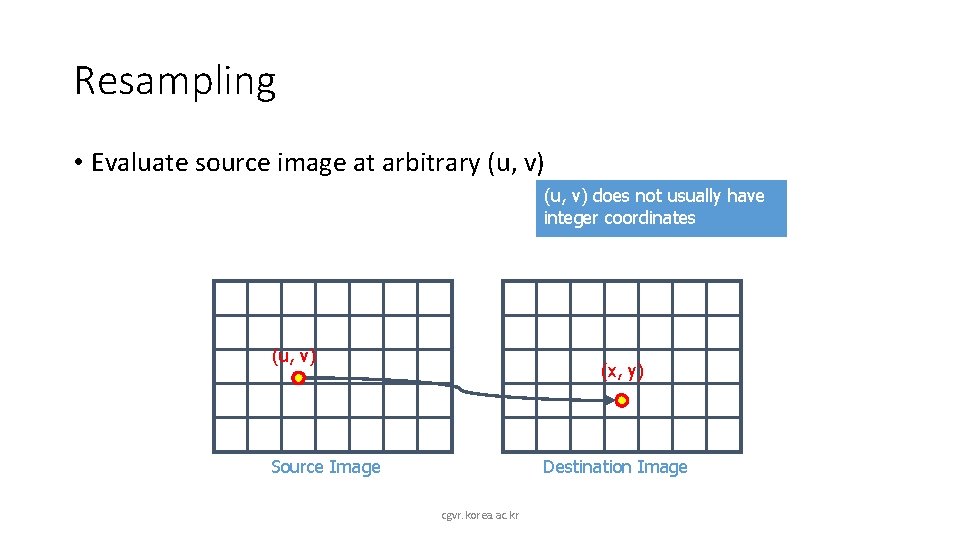
Resampling • Evaluate source image at arbitrary (u, v) does not usually have integer coordinates (u, v) (x, y) Source Image Destination Image cgvr. korea. ac. kr

Overview • Mapping • Forward • Reverse • Resampling • Point sampling • Triangle filter • Gaussian filter cgvr. korea. ac. kr

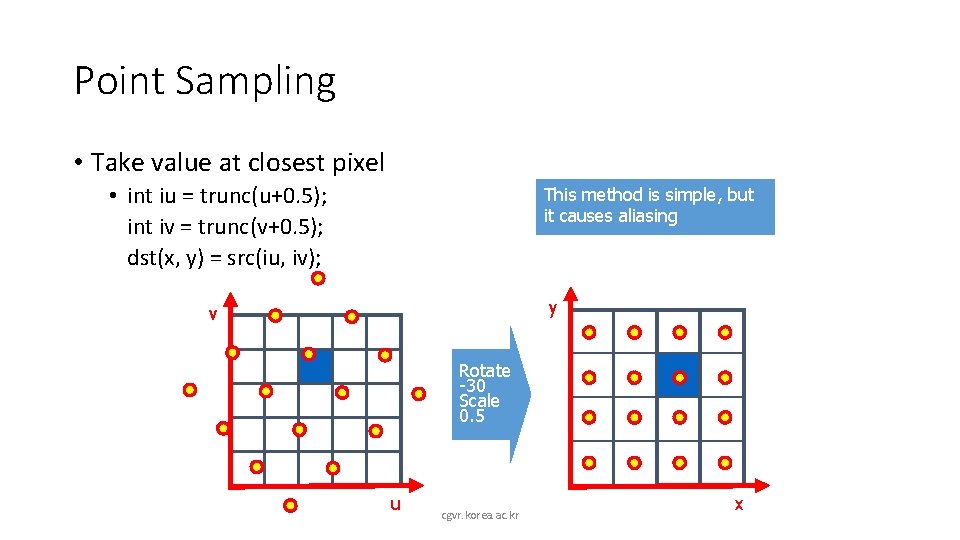
Point Sampling • Take value at closest pixel • int iu = trunc(u+0. 5); int iv = trunc(v+0. 5); dst(x, y) = src(iu, iv); This method is simple, but it causes aliasing y v Rotate -30 Scale 0. 5 u cgvr. korea. ac. kr x

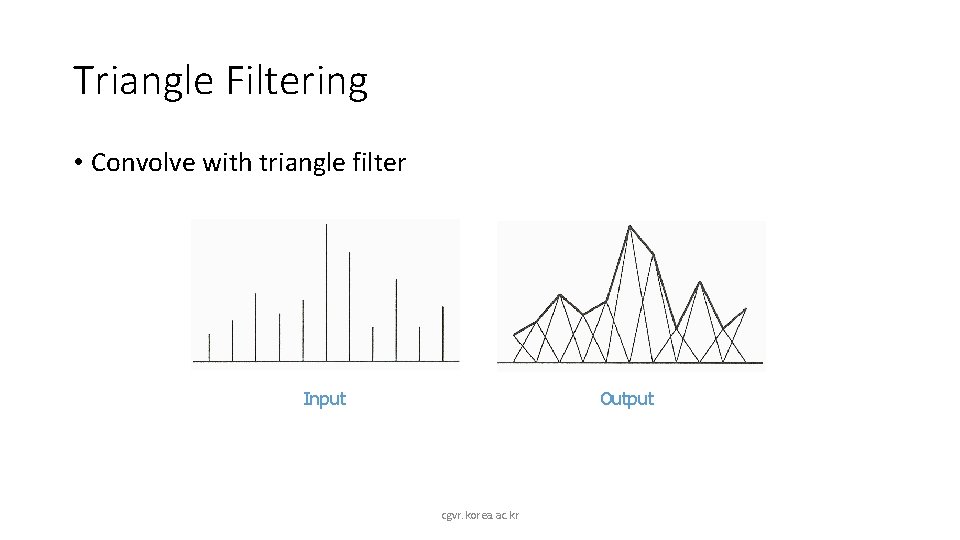
Triangle Filtering • Convolve with triangle filter Input Output cgvr. korea. ac. kr

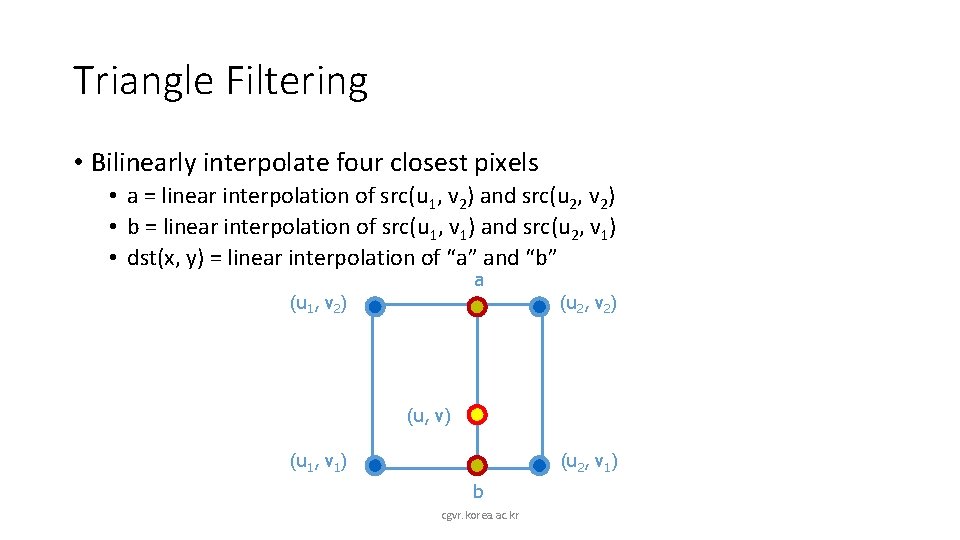
Triangle Filtering • Bilinearly interpolate four closest pixels • a = linear interpolation of src(u 1, v 2) and src(u 2, v 2) • b = linear interpolation of src(u 1, v 1) and src(u 2, v 1) • dst(x, y) = linear interpolation of “a” and “b” a (u 1, v 2) (u 2, v 2) (u, v) (u 1, v 1) (u 2, v 1) b cgvr. korea. ac. kr

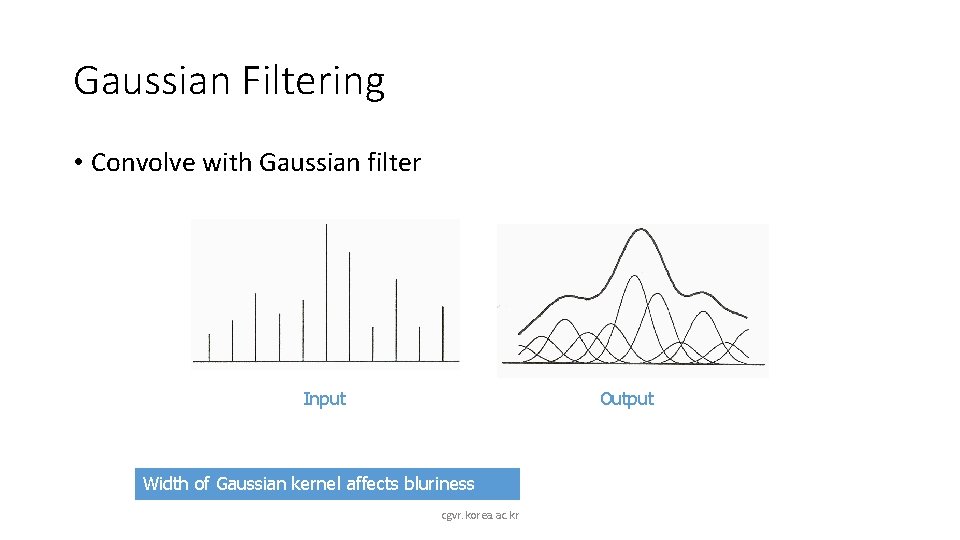
Gaussian Filtering • Convolve with Gaussian filter Input Output Width of Gaussian kernel affects bluriness cgvr. korea. ac. kr

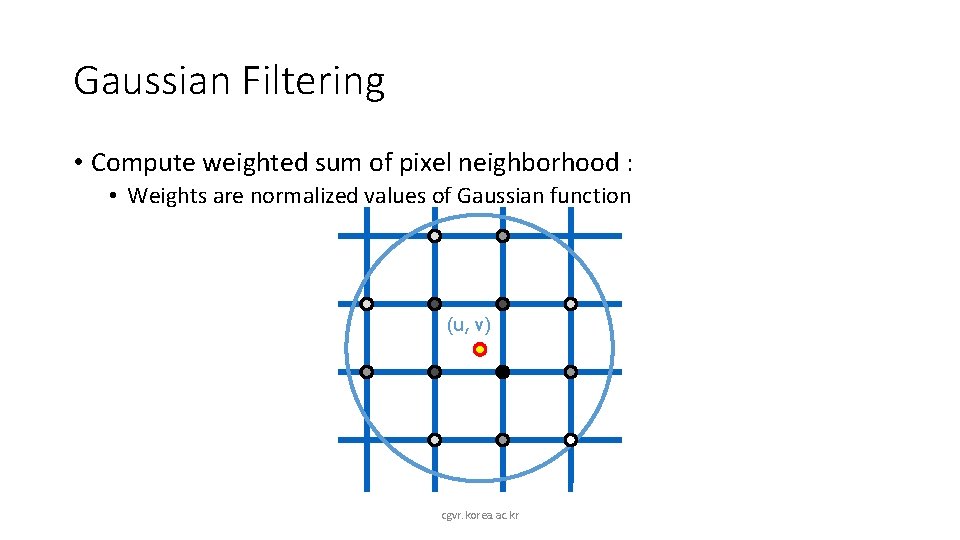
Gaussian Filtering • Compute weighted sum of pixel neighborhood : • Weights are normalized values of Gaussian function (u, v) cgvr. korea. ac. kr

Filtering Methods Comparison • Trade-offs • Aliasing versus blurring • Computation speed Point Bilinear cgvr. korea. ac. kr Gaussian

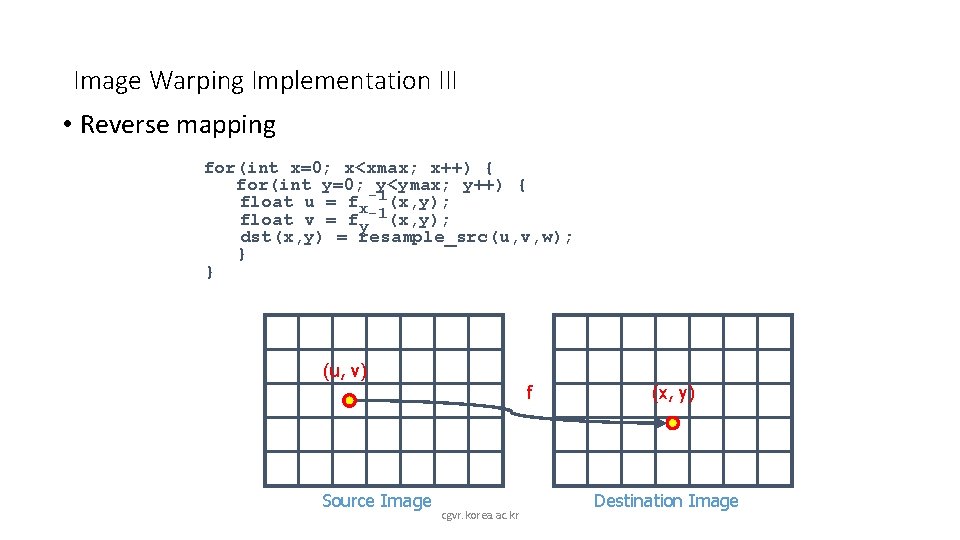
Image Warping Implementation III • Reverse mapping for(int x=0; x<xmax; x++) { for(int y=0; y<ymax; y++) { float u = fx-1(x, y); float v = fy-1(x, y); dst(x, y) = resample_src(u, v, w); } } (u, v) f Source Image cgvr. korea. ac. kr (x, y) Destination Image

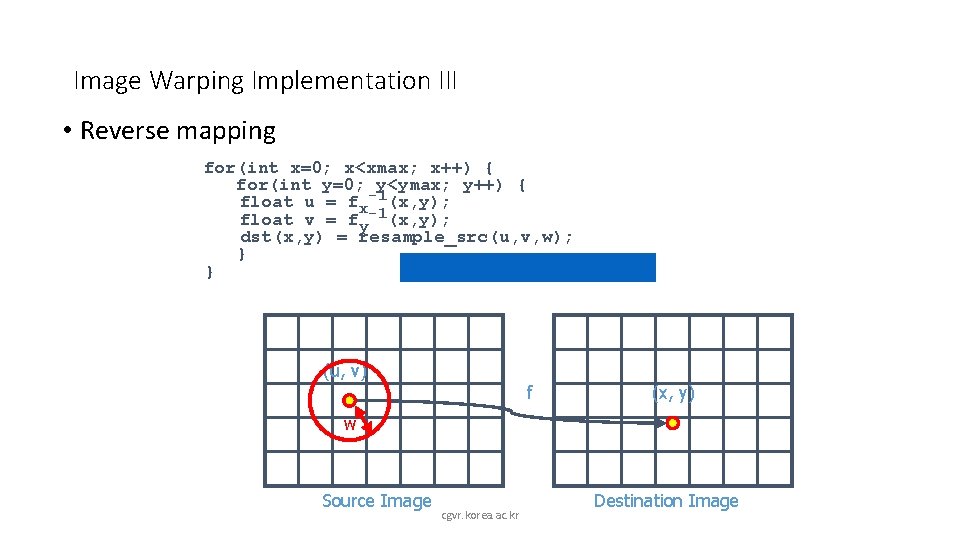
Image Warping Implementation III • Reverse mapping for(int x=0; x<xmax; x++) { for(int y=0; y<ymax; y++) { float u = fx-1(x, y); float v = fy-1(x, y); dst(x, y) = resample_src(u, v, w); } } (u, v) f (x, y) w Source Image cgvr. korea. ac. kr Destination Image

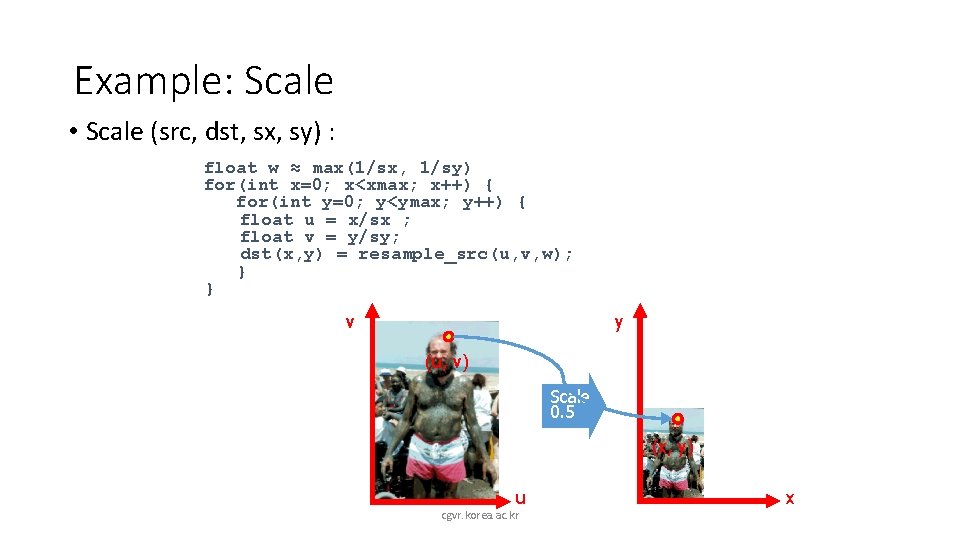
Example: Scale • Scale (src, dst, sx, sy) : float w ≈ max(1/sx, 1/sy) for(int x=0; x<xmax; x++) { for(int y=0; y<ymax; y++) { float u = x/sx ; float v = y/sy; dst(x, y) = resample_src(u, v, w); } } v y (u, v) Scale 0. 5 (x, y) u cgvr. korea. ac. kr x

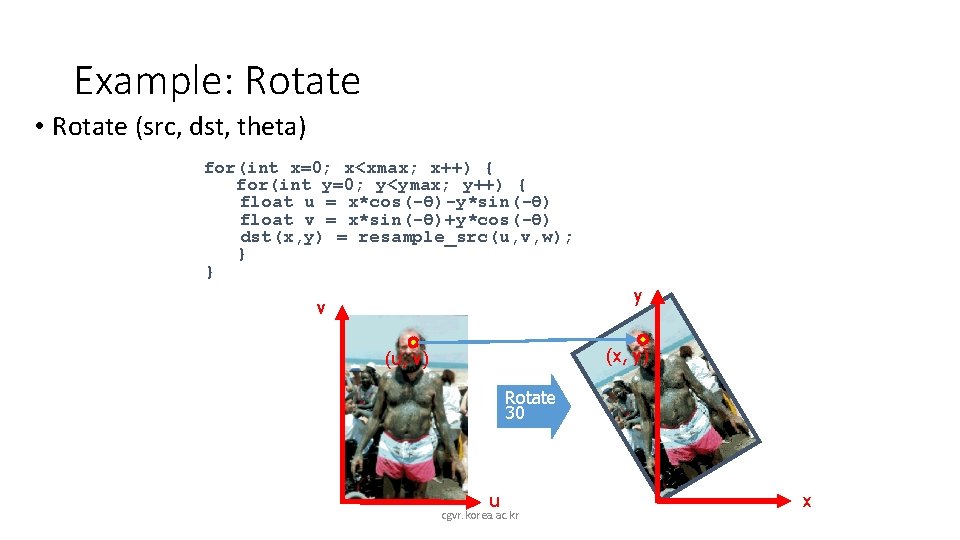
Example: Rotate • Rotate (src, dst, theta) for(int x=0; x<xmax; x++) { for(int y=0; y<ymax; y++) { float u = x*cos(-θ)-y*sin(-θ) float v = x*sin(-θ)+y*cos(-θ) dst(x, y) = resample_src(u, v, w); } } y v (x, y) (u, v) Rotate 30 u cgvr. korea. ac. kr x

Example: Fun • Swirl (src, dst, theta) for(int x=0; x<xmax; x++) { for(int y=0; y<ymax; y++) { float u = rot(dist(x, xcenter)*θ) float v = rot(dist(y, ycenter)*θ) dst(x, y) = resample_src(u, v, w); } } v (u, v) y (x, y) Swirl 45 u cgvr. korea. ac. kr x

Image Processing • Quantization • • Uniform quantization Random dither Ordered dither Floyd-Steinberg dither n Filtering n n n Warping n n n • Pixel operations • • Add random noise Add luminance Add contrast Add saturation n Blur Detect edge Scale Rotate Warps Combining n n cgvr. korea. ac. kr Morphs Composite

Image Processing • Quantization • • Uniform quantization Random dither Ordered dither Floyd-Steinberg dither n Filtering n n n Warping n n n • Pixel operations • • Add random noise Add luminance Add contrast Add saturation n Blur Detect edge Scale Rotate Warps Combining n n cgvr. korea. ac. kr Morphs Composite

Image Processing • Quantization • • Uniform quantization Random dither Ordered dither Floyd-Steinberg dither n Filtering n n n Warping n n n • Pixel operations • • Add random noise Add luminance Add contrast Add saturation n Blur Detect edge Scale Rotate Warps Combining n n cgvr. korea. ac. kr Morphs Composite

Overview • Image compositing • Blue-screen mattes • Alpha channel • Porter-Duff compositing algebra • Image morphing • Specifying correspondences • Warping • Blending cgvr. korea. ac. kr

Image Compositing • Separate an image into “elements” • Render independently • Composite together • Applications • Cel animation • Chroma-keying • Blue-screen matting Dobkin meets Elvis cgvr. korea. ac. kr

Blue-Screen Matting • Composite foreground and background images • Create background image • Create foreground image with blue background • Insert non-blue foreground pixels into background cgvr. korea. ac. kr

Alpha Channel • Encodes pixel coverage information • α = 0 : no coverage (or transparent) • α = 1 : full coverage (or opaque) • 0 < α < 1 : partial coverage (or semi-transparent) • Example : α = 0. 3 or Partial coverage Semi-Transparent cgvr. korea. ac. kr

Compositing with Alpha • Controls the linear interpolation of foreground and background pixels when elements are composited α=0 0< α < 1 α=1 cgvr. korea. ac. kr

Pixels with Alpha • Alpha channel convention : • • (r, g, b, α) represents a pixel that is α covered by the color C=(r/α, g/α, b/α) Color components are premultiplied by α Can display (r, g, b) values directly Closure in composition algebra • What is the meaning of the following? • • (0, 1, 0, 1) = (0, ½, 0, ½) = (0, ½, 0, 0) = cgvr. korea. ac. kr

Pixels with Alpha • Alpha channel convention : • • (r, g, b, α) represents a pixel that is α covered by the color C=(r/α, g/α, b/α) Color components are premultiplied by α Can display (r, g, b) values directly Closure in composition algebra • What is the meaning of the following? • • (0, 1, 0, 1) = full green, full coverage (0, ½, 0, 1) = half green, full coverage (0, ½, 0, ½) = full green, half coverage (0, ½, 0, 0) = no coverage cgvr. korea. ac. kr

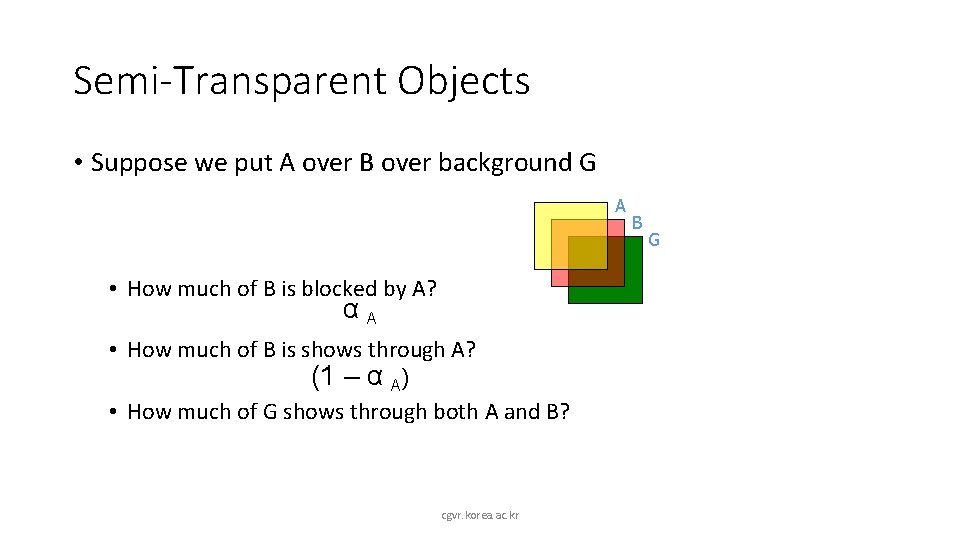
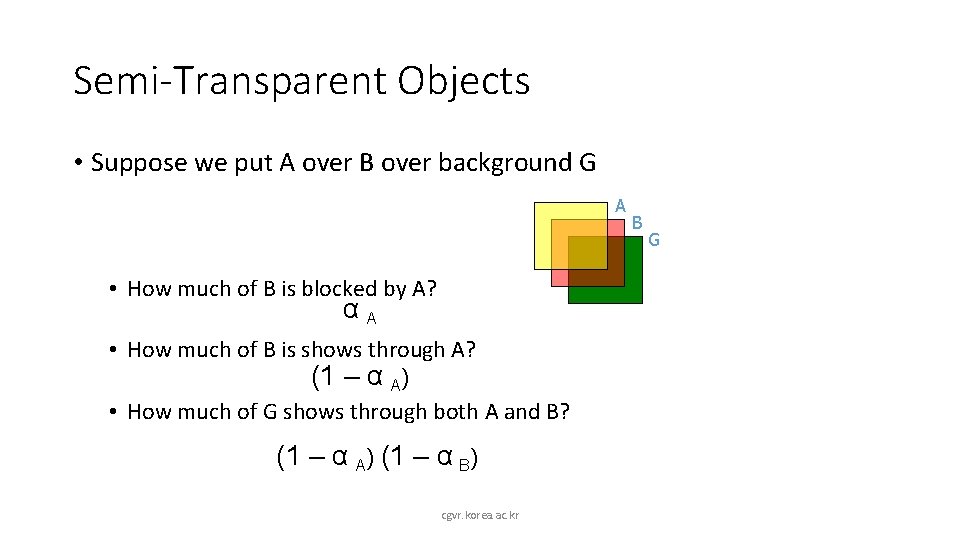
Semi-Transparent Objects • Suppose we put A over B over background G A • How much of B is blocked by A? cgvr. korea. ac. kr B G

Semi-Transparent Objects • Suppose we put A over B over background G A • How much of B is blocked by A? αA • How much of B is shows through A? cgvr. korea. ac. kr B G

Semi-Transparent Objects • Suppose we put A over B over background G A • How much of B is blocked by A? αA • How much of B is shows through A? (1 – α A) • How much of G shows through both A and B? cgvr. korea. ac. kr B G

Semi-Transparent Objects • Suppose we put A over B over background G A • How much of B is blocked by A? αA • How much of B is shows through A? (1 – α A) • How much of G shows through both A and B? (1 – α A) (1 – α B) cgvr. korea. ac. kr B G

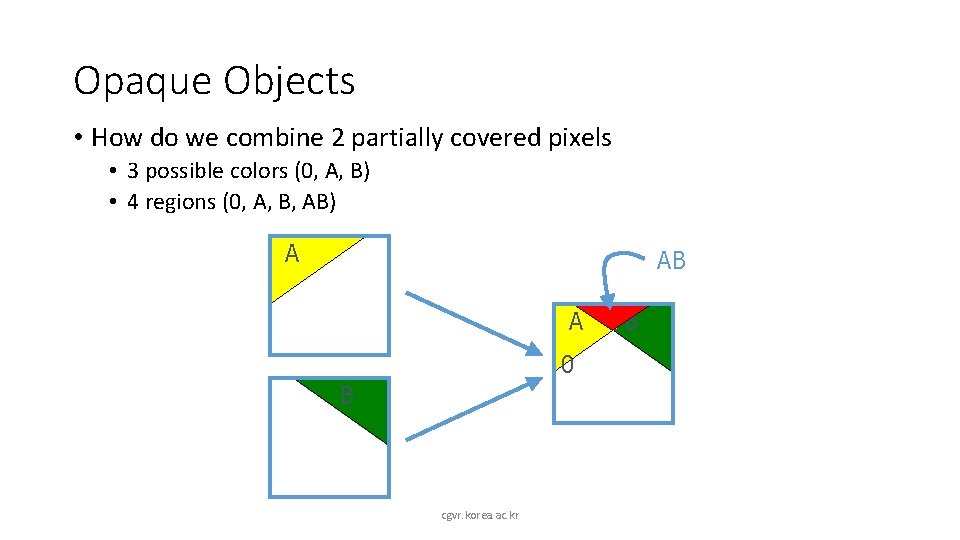
Opaque Objects • How do we combine 2 partially covered pixels • 3 possible colors (0, A, B) • 4 regions (0, A, B, AB) A AB A 0 B cgvr. korea. ac. kr B

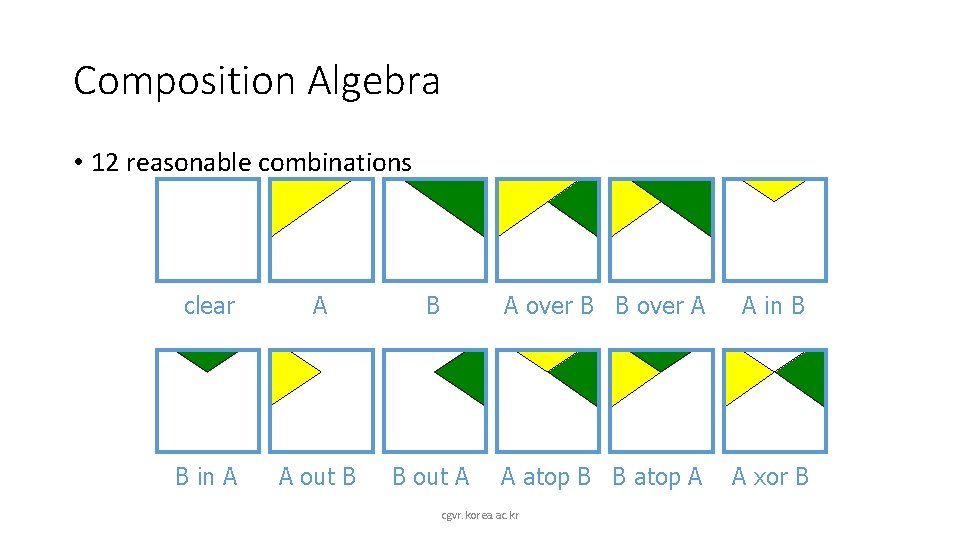
Composition Algebra • 12 reasonable combinations clear A B A over B B over A A in B B in A A out B B out A A atop B B atop A A xor B cgvr. korea. ac. kr

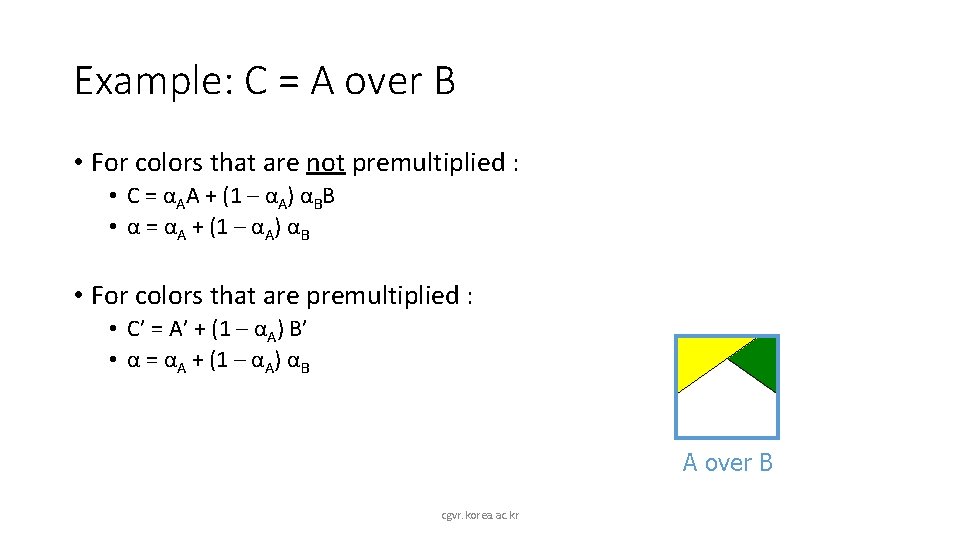
Example: C = A over B • For colors that are not premultiplied : • C = αAA + (1 – αA) αBB • α = αA + (1 – αA) αB • For colors that are premultiplied : • C’ = A’ + (1 – αA) B’ • α = αA + (1 – αA) αB A over B cgvr. korea. ac. kr

Image Composition Example Jurassic Park cgvr. korea. ac. kr

Overview • Image compositing • Blue-screen mattes • Alpha channel • Porter-Duff compositing algebra • Image morphing • Specifying correspondences • Warping • Blending cgvr. korea. ac. kr

Image Morphing • Animate transition between two images cgvr. korea. ac. kr

Cross-Dissolving • Blend image with “over” operator • Alpha of bottom image is 1. 0 • Alpha of top image varies from 0. 0 to 1. 0 cgvr. korea. ac. kr

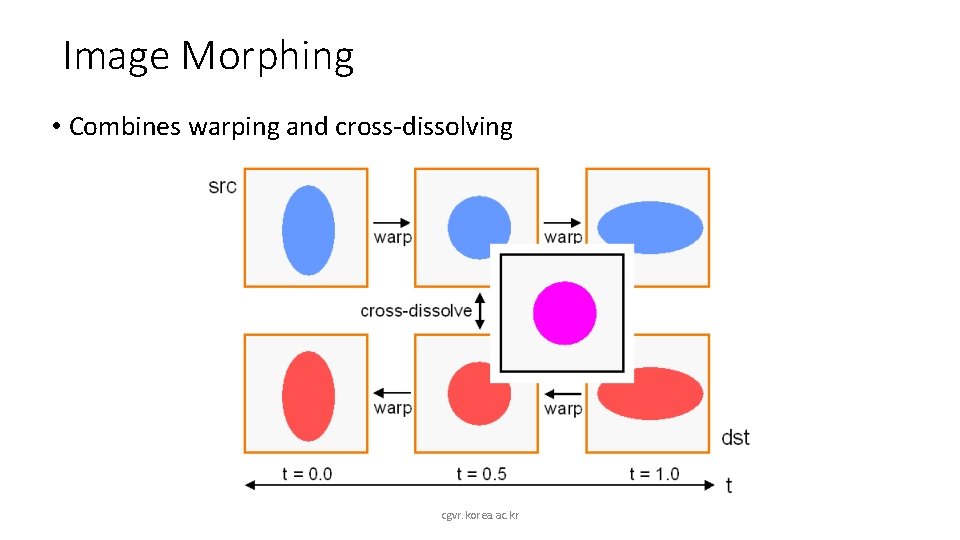
Image Morphing • Combines warping and cross-dissolving cgvr. korea. ac. kr

Image Morphing • The warping step is the hard one • Aim to align feature in images How specify mapping for the warp? cgvr. korea. ac. kr

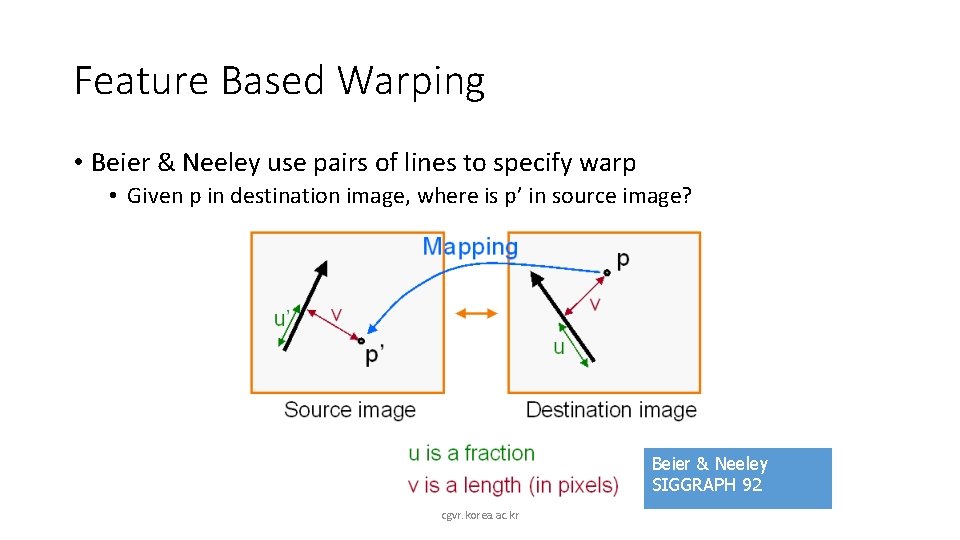
Feature Based Warping • Beier & Neeley use pairs of lines to specify warp • Given p in destination image, where is p’ in source image? Beier & Neeley SIGGRAPH 92 cgvr. korea. ac. kr

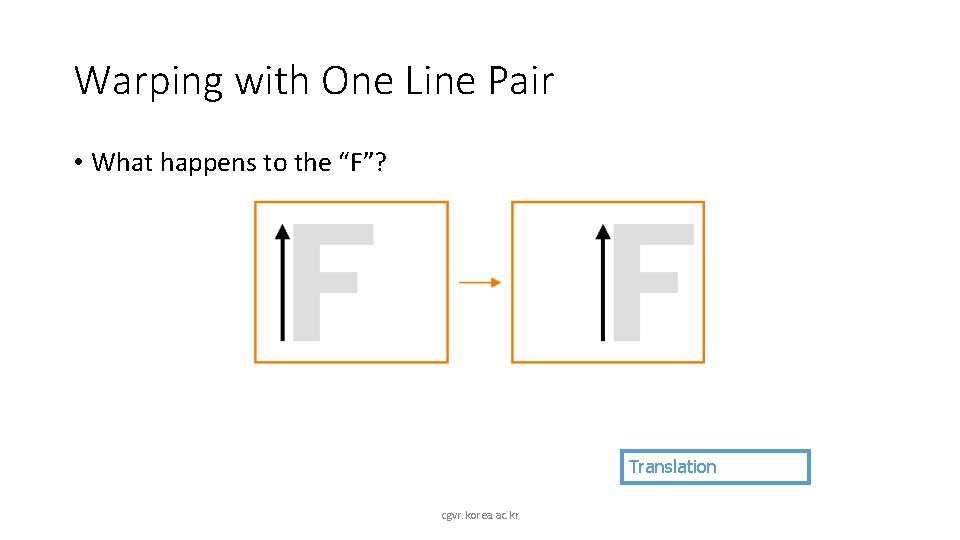
Warping with One Line Pair • What happens to the “F”? Translation cgvr. korea. ac. kr

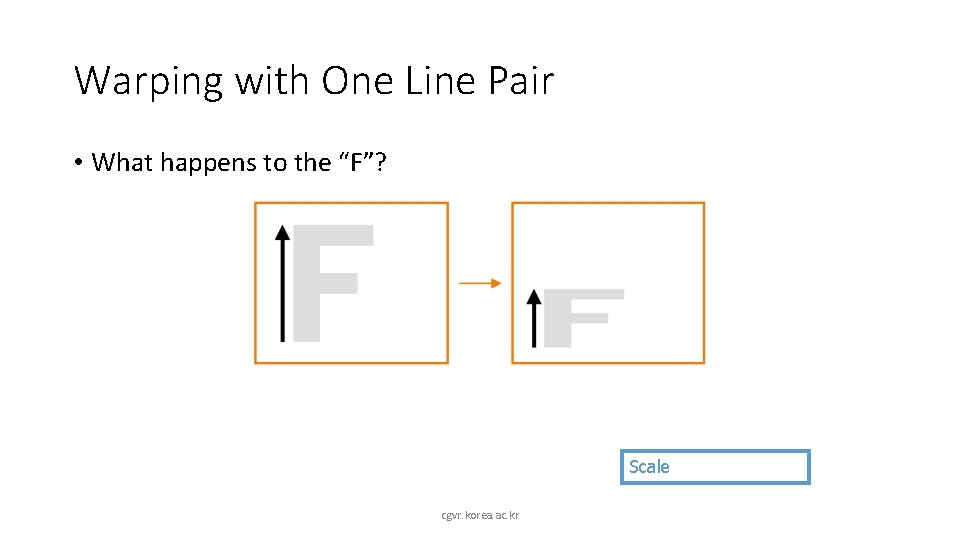
Warping with One Line Pair • What happens to the “F”? Scale cgvr. korea. ac. kr

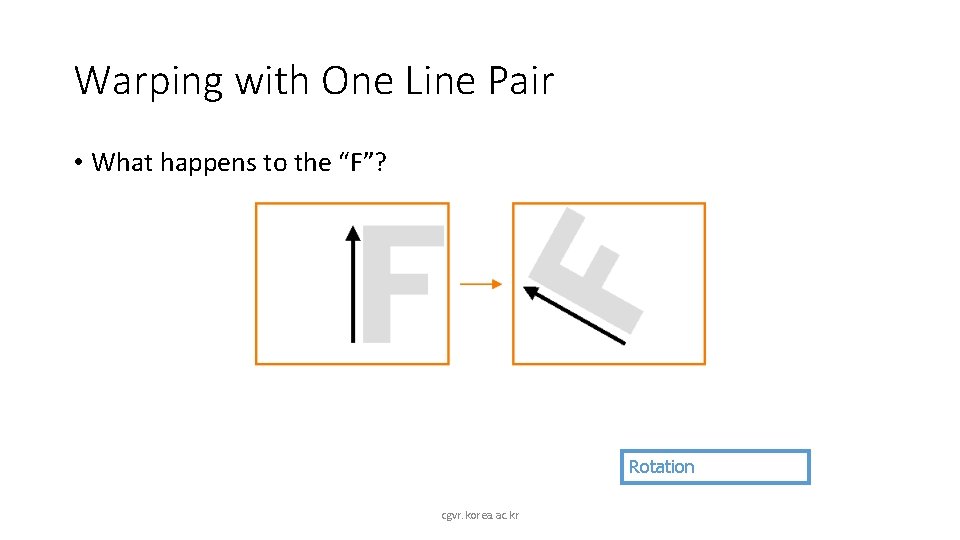
Warping with One Line Pair • What happens to the “F”? Rotation cgvr. korea. ac. kr

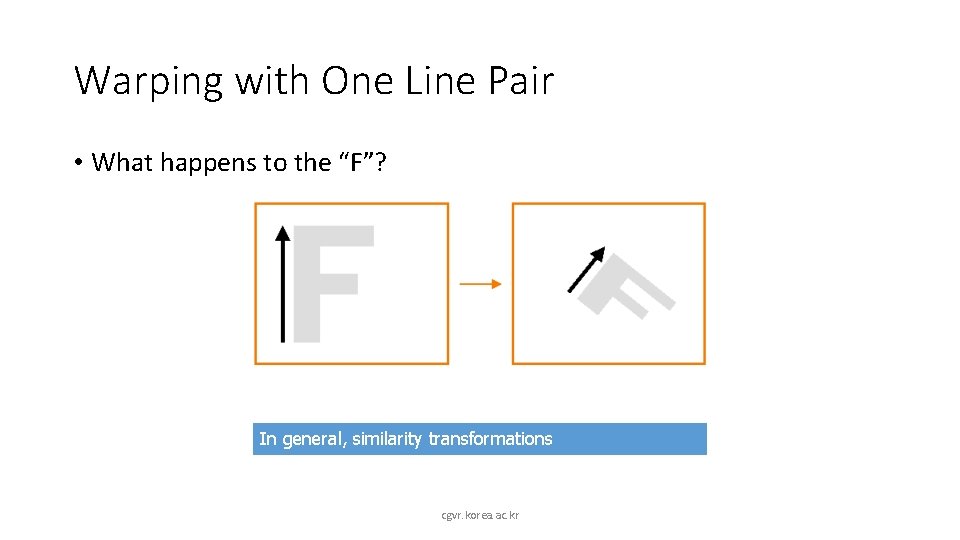
Warping with One Line Pair • What happens to the “F”? In general, similarity transformations cgvr. korea. ac. kr

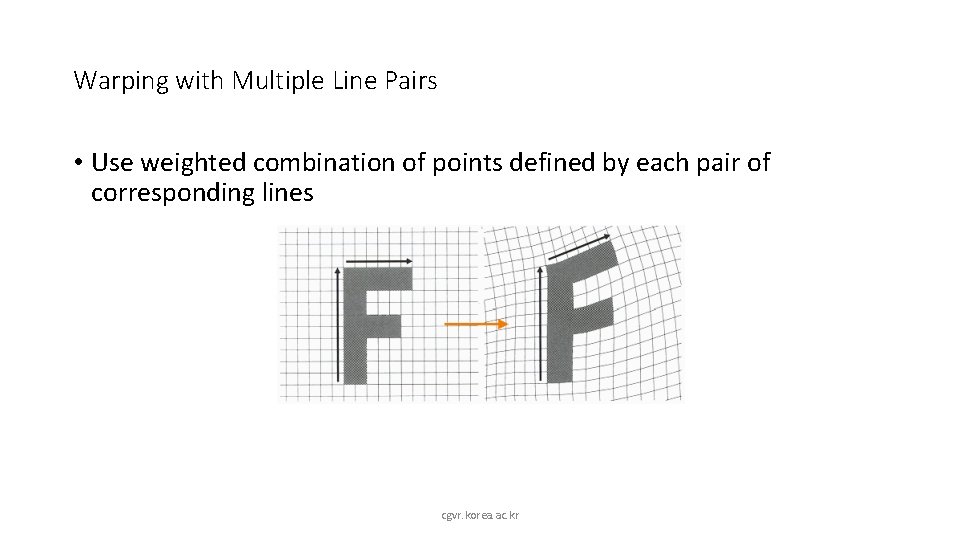
Warping with Multiple Line Pairs • Use weighted combination of points defined by each pair of corresponding lines cgvr. korea. ac. kr

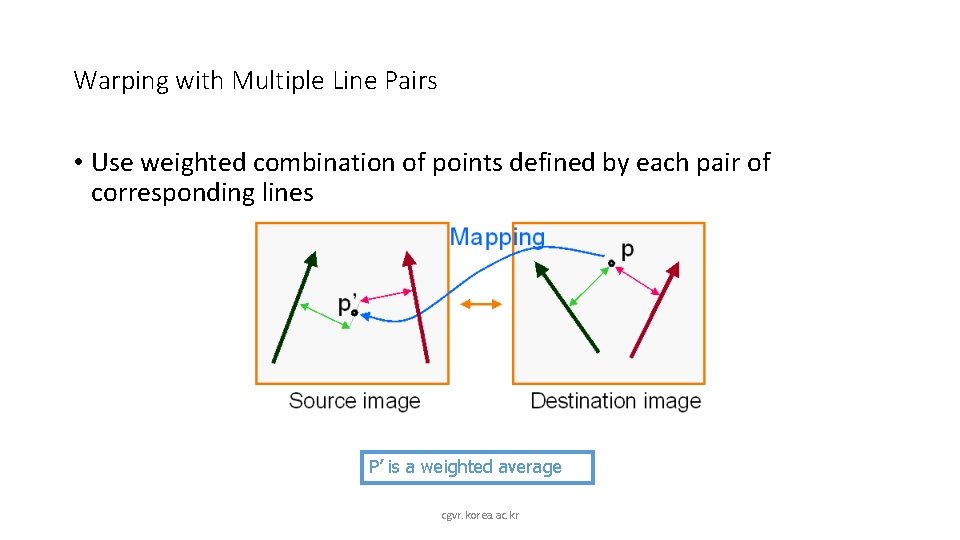
Warping with Multiple Line Pairs • Use weighted combination of points defined by each pair of corresponding lines P’ is a weighted average cgvr. korea. ac. kr

Weighting Effect of Each Line Pair • To weight the contribution of each line pair : Where • length[i] is the length of the i-th line • dist[i] is the distance from a point P to the i-th line • a, b, p are constants that control the wrap cgvr. korea. ac. kr

Warping Pseudocode Warp. Image(Image, L’[…], L[…]) Begin for each destination pixel p do psum = (0, 0) wsum = 0 for each line L[i] in destination do p’[i] = p transformed by (L[i], L’[i]) psum += p’[i] * weight[i] wsum += weight[i] end p’ = psum / wsum Result(p) = Image(p’) end cgvr. korea. ac. kr

Morphing Pseudocode Generate. Animation(Image 0, L 0[…], Image 1, L 1[…]) Begin for each intermediate frame time t do for i=1 to number of line pairs do L[i] = line t-th of the way from L 0[i] to L 1[i] end Warp 0 = Warp. Image(Image 0, L) Warp 1 = Warp. Image(Image 1, L) for each pixel p in Final. Image do Result(p) = (1 -t)*Warp 0 + t*Warp 1 end end cgvr. korea. ac. kr

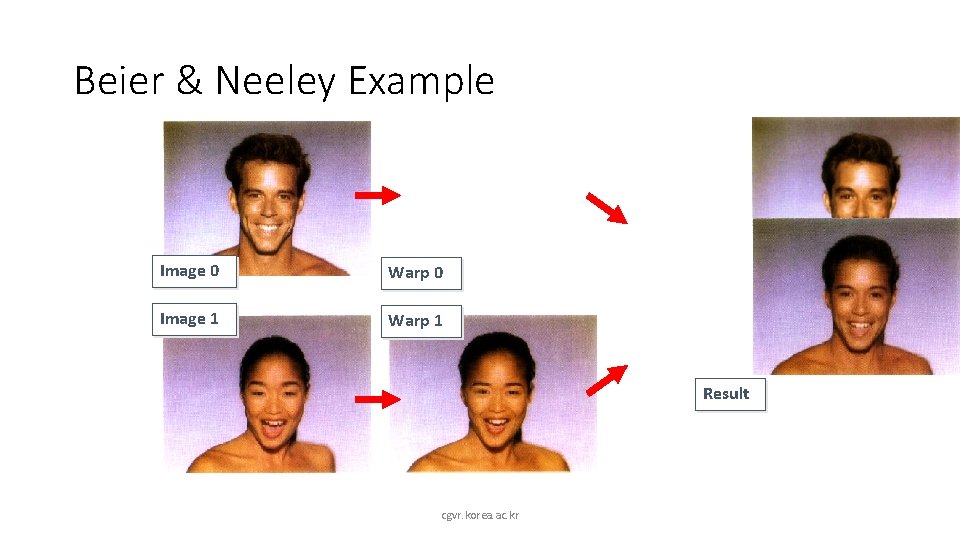
Beier & Neeley Example Image 0 Warp 0 Image 1 Warp 1 Result cgvr. korea. ac. kr

Beier & Neeley Example Image 0 Warp 0 Image 1 Warp 1 Result cgvr. korea. ac. kr

Image Processing • Quantization • • Uniform quantization Random dither Ordered dither Floyd-Steinberg dither n Filtering n n n Warping n n n • Pixel operations • • Add random noise Add luminance Add contrast Add saturation n Blur Detect edge Scale Rotate Warps Combining n n cgvr. korea. ac. kr Morphs Composite

Thanks… cgvr. korea. ac. kr