Image processing and neural networks Gregery T Buzzard

Image processing and neural networks Gregery T. Buzzard

Linear algebra • What are some of your favorite vectors of dimension at least one million?

Linear algebra • Here are some of my favorite vectors:

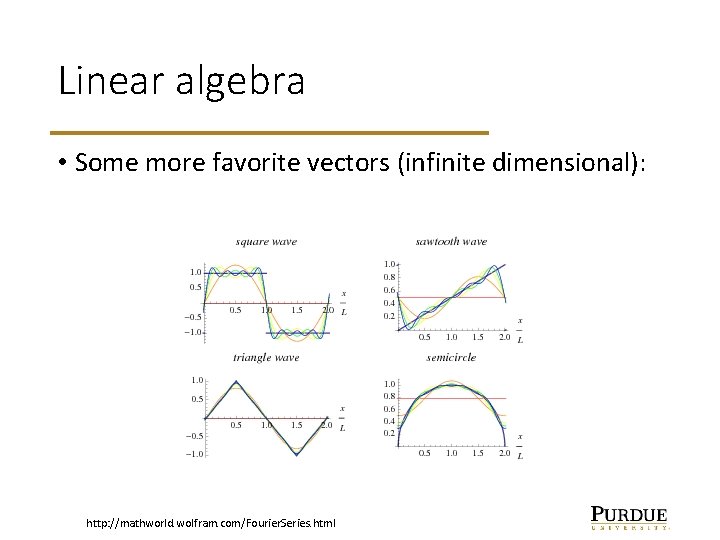
Linear algebra • Some more favorite vectors (infinite dimensional): http: //mathworld. wolfram. com/Fourier. Series. html

Linear algebra • What is a vector? • How do we represent a vector? • Basic answer: • Vector = ordered list of n real numbers • Basis = n vectors so that any vector can be written uniquely as a linear combination of these vectors http: //fourier. eng. hmc. edu/e 102/lectures/orthogonaltransform/node 3. html

High dimensional vectors • Note: images and signals are high-dimensional vectors. Can add and scale. • Q: What’s a ”good” basis for an image or signal? • Q: How can we represent an image in a given basis? • Q: Can we get by with less than a full basis – some kind of approximation?

Orthogonality • Inner product: • For vectors in Rn: • For real-valued functions: • Orthogonal (perpendicular): inner product is 0. https: //en. wikipedia. org/wiki/Dot_product

Orthogonality • Orthogonality gives a firm (and fast) foundation! • With a basis of pairwise orthogonal unit vectors, we can represent a vector in a basis using dot product: a = <a, e 1> e 1 + <a, e 2 > e 2 + … + <a, en > en • Standard basis vectors slide a single nonzero element over each coordinate. https: //www. yogawinetravel. com/how-to-get-the-most-out-of-your-visit-to-the-piazza-del-duomo-in-pisa-italy/

Orthogonality • Orthogonal expansion for images and signals: • Fourier series http: //www. bragitoff. com/2016/03/fourier-series-and-scilab/

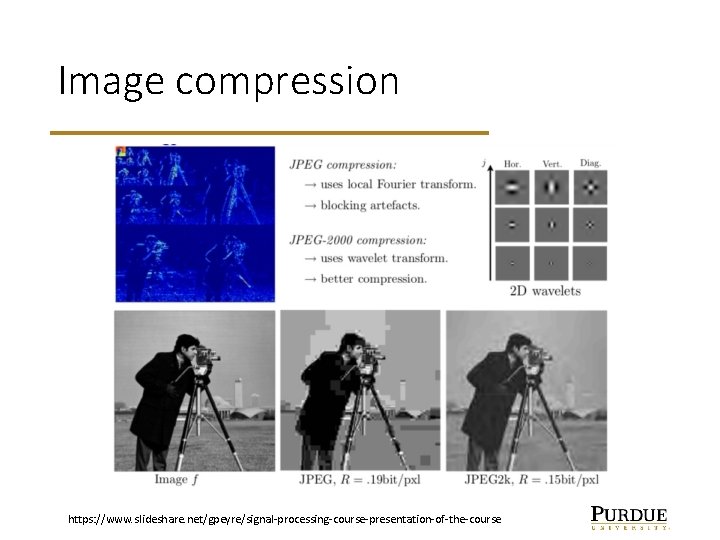
Image compression https: //www. slideshare. net/gpeyre/signal-processing-course-presentation-of-the-course

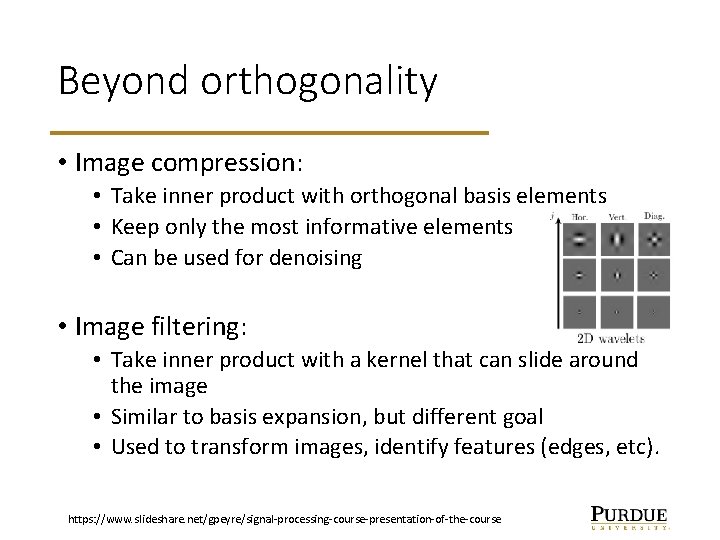
Beyond orthogonality • Image compression: • Take inner product with orthogonal basis elements • Keep only the most informative elements • Can be used for denoising • Image filtering: • Take inner product with a kernel that can slide around the image • Similar to basis expansion, but different goal • Used to transform images, identify features (edges, etc). https: //www. slideshare. net/gpeyre/signal-processing-course-presentation-of-the-course

More general maps • Limitation: Basis expansion and filtering are linear: • F(av + bu) = a. F(v) + b. F(u) • How do we map from images to a discrete classification like {cat, not cat}? https: //en. wiktionary. org/wiki/cat https: //www. kickstarter. com/projects/vat 19/the-not-a-cat-the-worlds-first-cat-that-isnt

Internal representation • Nonlinear low dimensional representation from high-dimensional data • Input: 28 x 28 grayscale digits • Compare random images: • Low-dimensional representations of digits: PCA Graph: repelling particles + springs http: //colah. github. io/posts/2014 -10 -Visualizing-MNIST/ t-SNE: stochastic neighbor embedding

Image classification • Convert image to low dimensional representation, then to classification. • Given n distinct classes, use the softmax function to give probabilities: • X = (x 1, …, xn) is a vector of real numbers • S(X) = (exp(x 1), …, exp(xn)) / (exp(x 1) + … + exp(xn)) is a vector of positive numbers that add to 1: interpret as “probability” • Map images to probabilities for each class using softmax function S(X).

First attempt at an image classifier • Input an image = X • Apply a linear map. E. g. , inner product with various kernels to identify features. X -> AX • Apply the softmax function to estimate correct classification https: //science. howstuffworks. com/transport/flight/classic/ten-bungled-flight-attempt. htm

Problems • Dimension of AX must equal number of classes. • How do we know what features to use? • Do we really want to weight the absence of a feature as much as the presence of a feature? • Do we really want to use linear maps up to the final step?

More general classifier • Use activation units: Re. LU or rectified unit or similar functions to identify the presence of features. • Stack multiple layers using • • Convolutional layer (inner product) Re. LU Max pool Fully connected https: //en. wikipedia. org/wiki/Rectifier_(neural_networks)

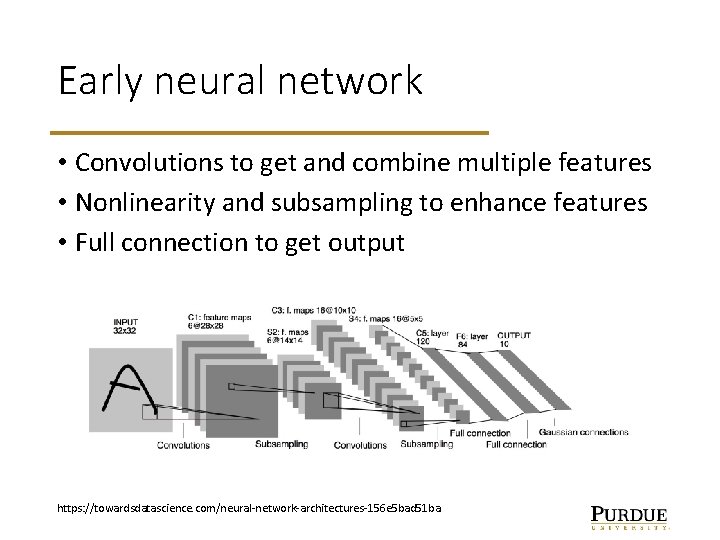
Early neural network • Convolutions to get and combine multiple features • Nonlinearity and subsampling to enhance features • Full connection to get output https: //towardsdatascience. com/neural-network-architectures-156 e 5 bad 51 ba

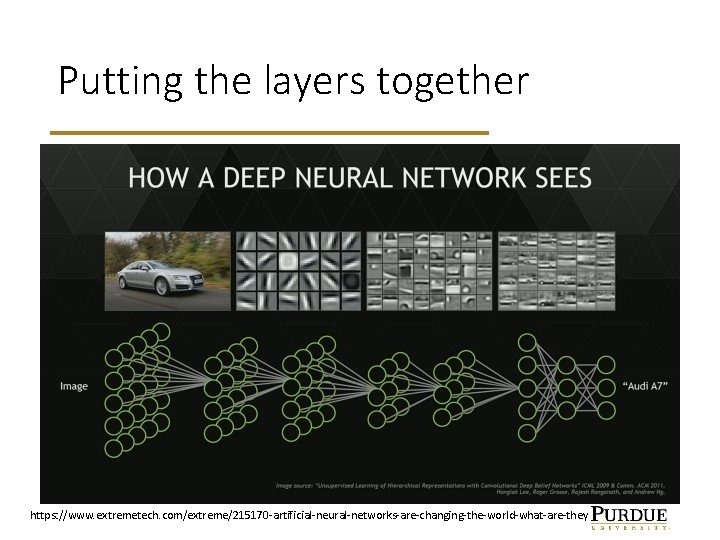
Putting the layers together https: //www. extremetech. com/extreme/215170 -artificial-neural-networks-are-changing-the-world-what-are-they

Questions • How do we choose the architecture? • (and do we need multiple layers)? • How do we choose the features? • How well does it work?

Do we need multiple layers? • Universal approximation theorem: • a feed-forward network with a single hidden layer containing a finite number of neurons (i. e. , a multilayer perceptron), can approximate continuous functions on compact subsets of Rn, under mild assumptions on the activation function. • Beautiful mathematical result, but not practical for learning and efficient representation. https: //en. wikipedia. org/wiki/Universal_approximation_theorem http: //aeronauticpictures. com/buy/download/t/early-flight_stock-footage/

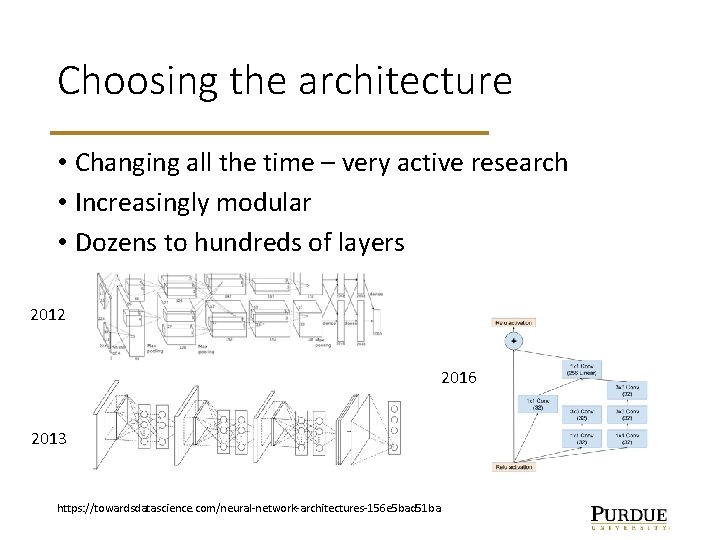
Choosing the architecture • Changing all the time – very active research • Increasingly modular • Dozens to hundreds of layers 2012 2016 2013 https: //towardsdatascience. com/neural-network-architectures-156 e 5 bad 51 ba

Choosing features: training • Instead of choosing features, we’ll learn them. • Need training data: input-output pairs • Need an error function – how good is our output? • Need an update mechanism: backpropagation

Backpropagation • Input, X, produces output, Y. Output depends on parameters, �� , (kernel/filter/weights between nodes). • Training data is set of known pairs ( Xi , Yi ) • Error function, E(X, �� ) gives the error between calculated output and desired output • Use gradient descent to change parameter values

Backpropagation • Input-output calculation flows forwards, gradient flows backwards f = qz; q = x+y Dff = 1; Dqf = z, Dzf = q Dxq = 1, Dyq = 1 Dxf = (Dqf)(Dxq) = z, Dyf = (Dqf)(Dyq) = z, Dzf = q = x+y http: //cs 231 n. github. io/optimization-2/

Generative vs. Discriminative • Discriminative models learn the boundary between classes • Take an input image and produce a classification. • Generative models model the distribution of individual classes • Take a class label and some parametrization of that class and produce an example image.

Autoencoders • Autoencoders learn a reduced dimension representation of input. • Can be paired with a decoder to recover the input. • Applying random input to the decoder generates samples from the distribution on input.

GANs: Generative Adversarial Networks • Paired networks: one discriminates real from fake, another generates examples to pass as real. • Double feedback loop: • Generator takes random input and returns an image. • Discriminator takes in both real and fake images and returns probability of real. • Both get feedback about the other. https: //deeplearning 4 j. org/generative-adversarial-network

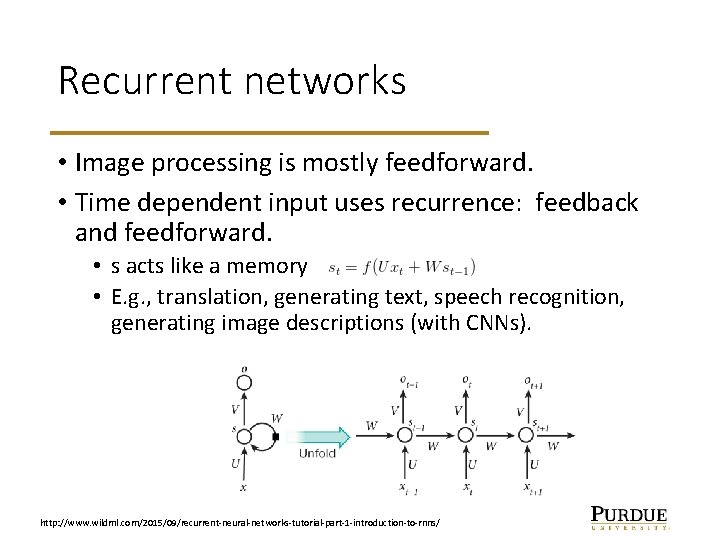
Recurrent networks • Image processing is mostly feedforward. • Time dependent input uses recurrence: feedback and feedforward. • s acts like a memory • E. g. , translation, generating text, speech recognition, generating image descriptions (with CNNs). http: //www. wildml. com/2015/09/recurrent-neural-networks-tutorial-part-1 -introduction-to-rnns/

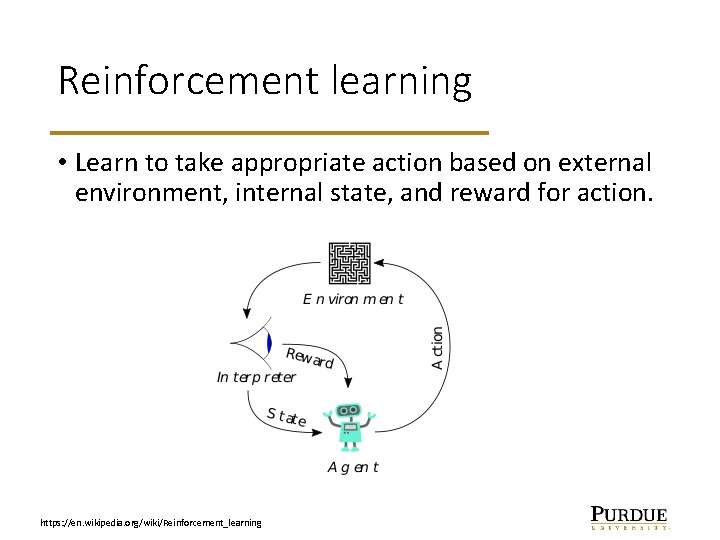
Reinforcement learning • Learn to take appropriate action based on external environment, internal state, and reward for action. https: //en. wikipedia. org/wiki/Reinforcement_learning

What can they do? • Image classification, segmentation, denoising, etc. • Facial recognition and object recognition • Speech recognition and generation • Real time spoken translation • Cancer detection and other healthcare • Robot learning by demonstration • Recommender systems • Image generation: • https: //www. geek. com/tech/nvidia-ai-generates-fake-faces-based-on-real-celebs-1721216/

How well do they work? https: //www. slideshare. net/David. Balduzzi/game-theory-for-neural-networks

How do they fail? Adversarial attacks https: //medium. com/deep-dimension/deep-learning-papers-review-universal-adversarial-patch-a 5 ad 222 a 62 d 2

Techniques for building/training • Structure • Layer components: Convolution, Re. LU, max pool, full linear, gated recurrent, etc. • Hyperparameters: Number of layers, kernel width, padding • Training: • • • Performance metric and baseline/goal Data – how much and how to use? Optimizer: SGD+Nestorov, Adam (adaptive moment estimation). Minibatches, dropout, batch normalization, regularization. Hyperparameters: learning rate, dropout rate, regularization weight • Start from a successful structure for a similar problem.

Mathematical questions • Why do they work well? • How do they approximate a function on a high-dim’l space? • How do they generalize to new examples? • Is there a mathematical explanation for how to choose architecture? • How can we train them more quickly with fewer examples? • What layers might be better than existing layers? • How can we make them more robust? • How can we combine multiple sources of expertise?