Image Processing and Computer Vision 3 Morphology Structural

Image Processing and Computer Vision: 3

Morphology Structural processing of images Image Processing and Computer Vision: 3

Morphological Transformations n Set theoretic methods of extracting quantitative descriptions of image components n n n Boundaries Skeletons Convex hull Mainly binary, sometimes greylevel Two fundamental operations n Erode, dilate Image Processing and Computer Vision: 3 3

Thresholding n n Morphological operations usually applied to bilevel images (black and white) Generated by thresholding n n Greyscale Colour Image Processing and Computer Vision: 3 4

Thresholding Greyscale Images n Previous lecture If g(x, y) > q then g(x, y) = 1 else g(x, y) = 0 Image Processing and Computer Vision: 3 5

Thresholding Colour Images n Partition colour cube: if cr(x, y) > qr AND cg(x, y) > qg AND cb(x, y) > qb then c(x, y) = 1 else c(x, y) = 0 Image Processing and Computer Vision: 3 6

Thresholding Colour Images n Colour matching Image Processing and Computer Vision: 3 7

Preliminary Notation n Translation of a region by x n Reflection of a region Image Processing and Computer Vision: 3 8

Binary Erode n Formally n Informally n n place the structuring element on a pixel of the object remove that pixel if the structuring element overlaps a non-object pixel Image Processing and Computer Vision: 3 9

Binary Dilate n Formally n Informally n All pixels covered by structuring element placed at all locations on region Image Processing and Computer Vision: 3 10

Binary Open and Close n n n Erosion shrinks an object Dilation expands it Can combine operators Open = erosion then dilation Close = dilation then erosion Image Processing and Computer Vision: 3 11

Binary Open n Opening smoothes regions n n Removes spurs Breaks narrow lines Image Processing and Computer Vision: 3 12

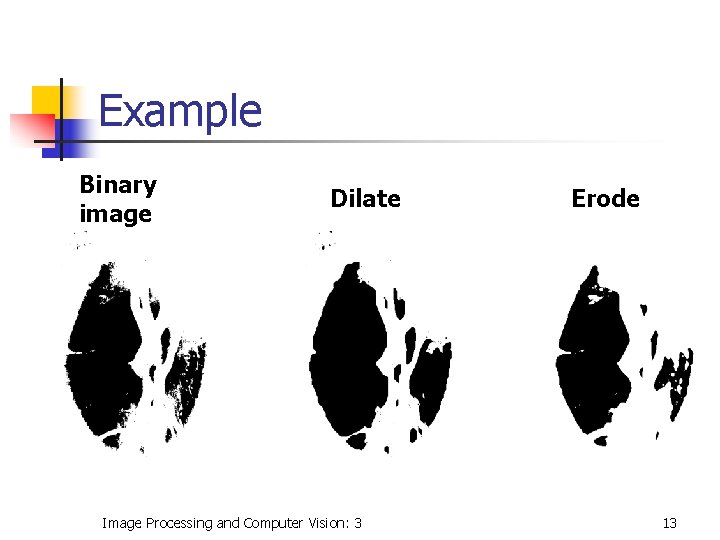
Example Binary image Dilate Image Processing and Computer Vision: 3 Erode 13

Binary Close n Closing fills gaps n n Holes in region Narrow gaps Image Processing and Computer Vision: 3 14

Processing grey scale images n n Same methods can be applied to greyscale images Slight redefinition Image Processing and Computer Vision: 3 15

Greyscale Erode n Set operation replaced by min operation n Output at a point is minimum of image pixel and structuring element pixel Image Processing and Computer Vision: 3 16

Greyscale Dilate n Set operation replaced by max operation n Output is maximum of image and structuring element Image Processing and Computer Vision: 3 17

Examples Erode Image Processing and Computer Vision: 3 Dilate 18

Distance n n Applies to binary images For each pixel in a region distance 0 0 0 1 1 1 0 0 n = minimum path to outside 0 0 0 0 1 1 1 0 0 0 1 2 1 0 0 0 1 1 1 0 0 0 0 Image Processing and Computer Vision: 3 19

Computation n Use erosion n n Label removed pixel with iteration number Use relationship operator n f(i, j) are neighbours of f(x, y) Image Processing and Computer Vision: 3 20

Skeleton n n Reduces regions of a binary image to lines one pixel thick Preserves n n n Shape Continuity How? Uses? Image Processing and Computer Vision: 3 21

Algorithms n Thinning n n n Repeatedly thin image Retain end points and connections Distance Transform n n Skeleton lies along discontinuities Sort of local maxima or ridges Image Processing and Computer Vision: 3 22

Applications n n Shape representation, maintaining topology Character recognition Image Processing and Computer Vision: 3 23

Convex Hull Convex hull follows outline of object, except for concavities. Number and shape of regions between convex hull and object are characteristic of object shape. Image Processing and Computer Vision: 3 24

Summary n Binary morphology n n Greyscale morphology n n Erode, dilate, open, close Erode, dilate Distance Skeleton Convex Hull Image Processing and Computer Vision: 3 25

Computers in the future may weigh no more than 1 ½ tons Popular Mechanics, 1949 Image Processing and Computer Vision: 3 26