Image method for the Greens functions of annulus

Image method for the Green’s functions of annulus and half-plane Laplace problems Reporter: Shiang-Chih Shieh Authors: Shiang-Chih Shieh, Ying-Te Lee and Jeng-Tzong Chen Department of Harbor and River Engineering, National Taiwan Ocean University Oct. 22, 2008 October, 22, 2008 p. 1

Outline Introduction Problem statements Analytical solution ü ü Method of Fundmental Solution (MFS) Trefftz method Equivalence of Trefftz method and MFS Semi-analytical solution Numerical examples Conclusions 2

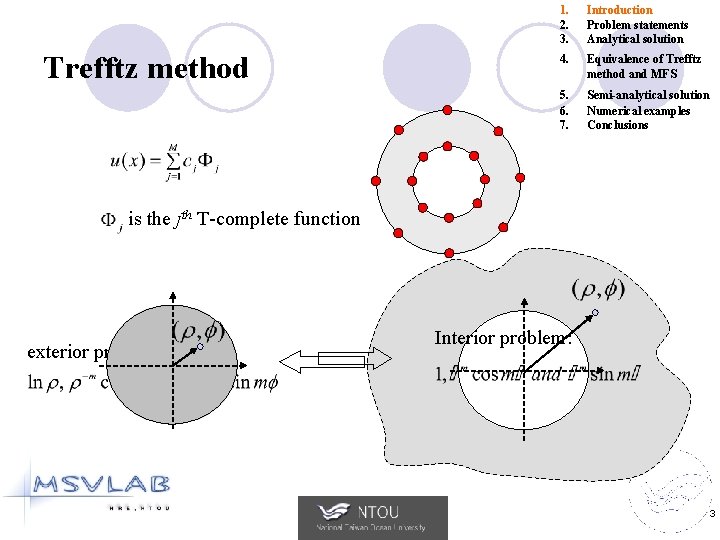
Trefftz method 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions is the jth T-complete function exterior problem: Interior problem: 3

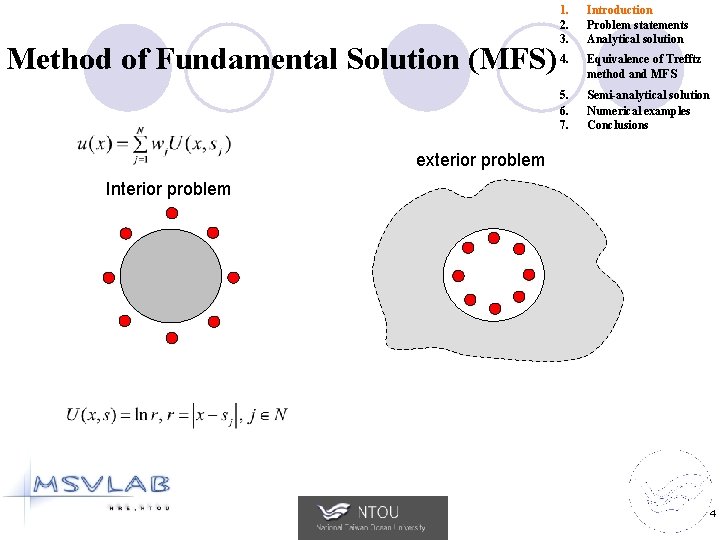
Method of Fundamental Solution (MFS) 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions exterior problem Interior problem 4

Trefftz method and MFS Method Trefftz method 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions MFS Definition Figure caption u(x) s r D D Base u(x) , (T-complete function) , r=|x-s| G. E. Match B. C. Determine cj Determine wj is the number of complete functions is the number of source points in the MFS 5

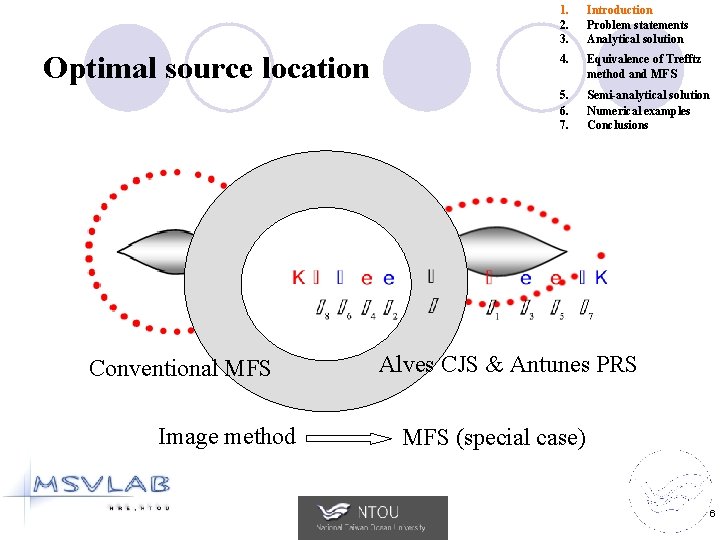
Optimal source location Conventional MFS Image method 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions Alves CJS & Antunes PRS MFS (special case) 6

Problem statements 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions Case 1 Annular Governing equation : t 1=0 u 2=0 a b Boundary condition : Fixed-Free boundary 7

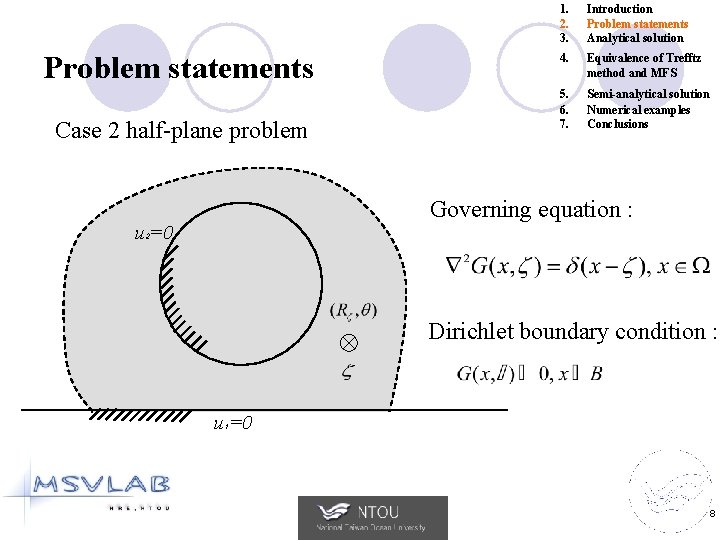
Problem statements Case 2 half-plane problem 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions Governing equation : u =0 2 Dirichlet boundary condition : u =0 1 8

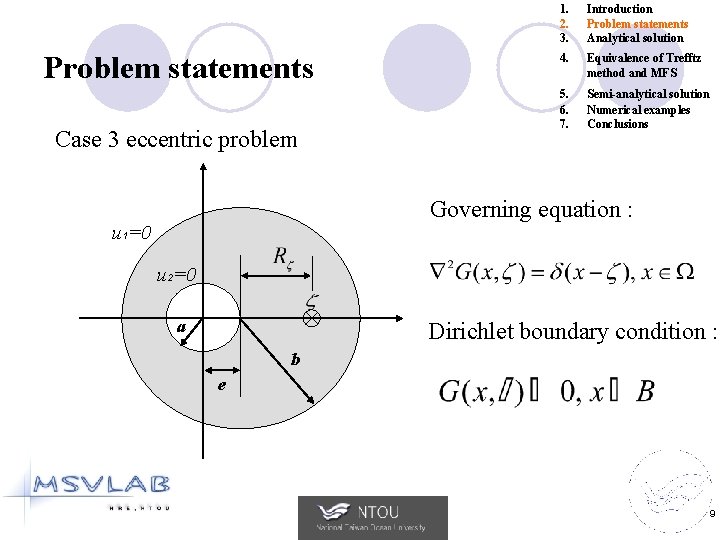
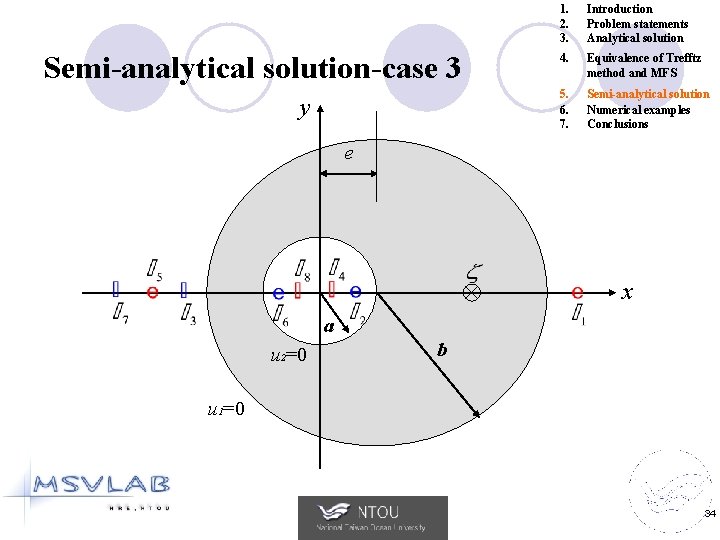
Problem statements Case 3 eccentric problem 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions Governing equation : u 1=0 u 2=0 a Dirichlet boundary condition : b e 9

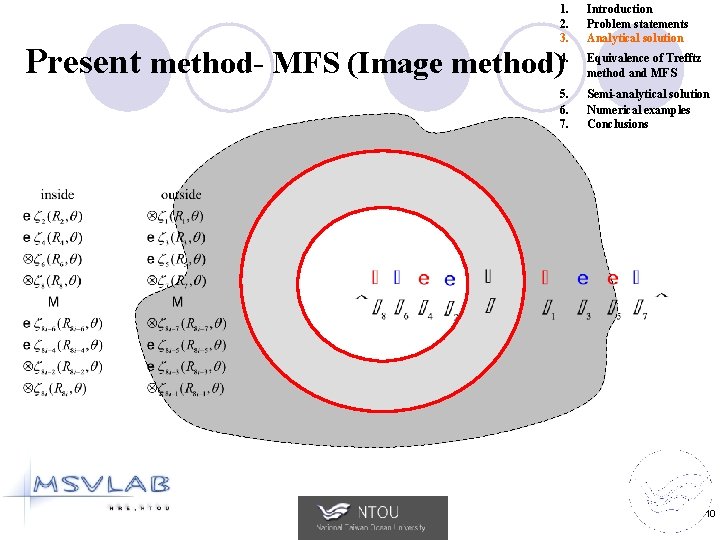
1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions Present method- MFS (Image method) 10

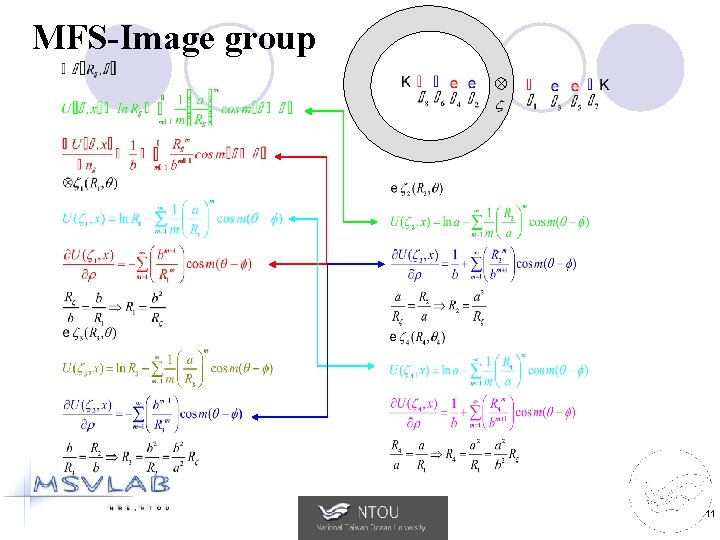
MFS-Image group 11

MFS-Image group 12

Analytical derivation 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions 13

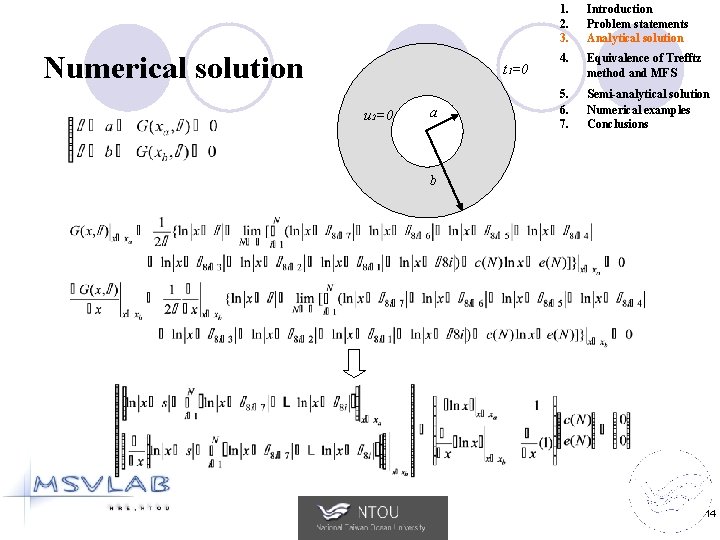
Numerical solution t 1=0 u 2=0 a 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions b 14

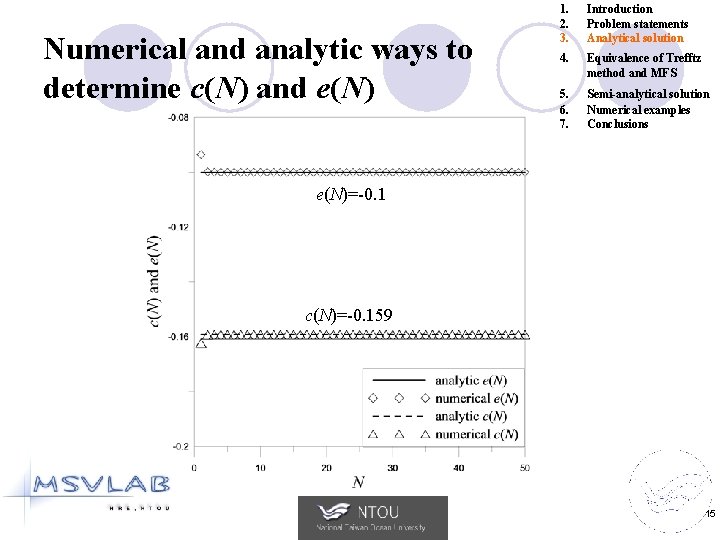
Numerical and analytic ways to determine c(N) and e(N) 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions e(N)=-0. 1 c(N)=-0. 159 15

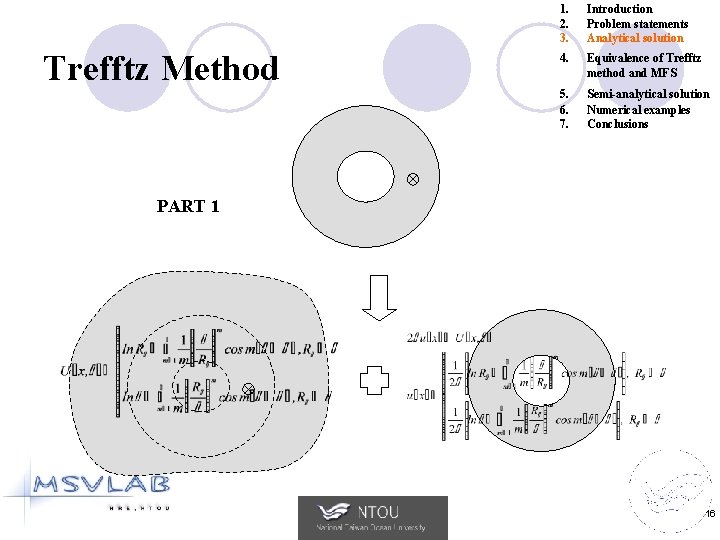
Trefftz Method 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions PART 1 16

Boundary value problem 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions PART 2 17

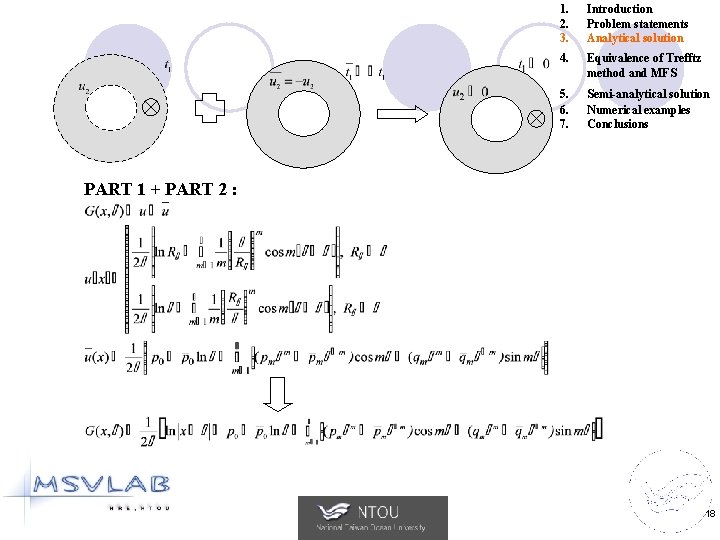
1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions PART 1 + PART 2 : 18

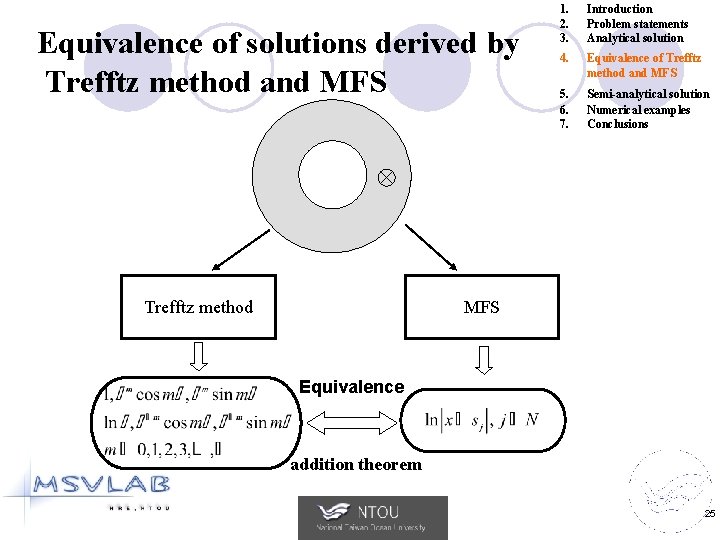
Equivalence of solutions derived by using Trefftz method and MFS for annular problem 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions MFS(Image method) The same Trefftz method 19

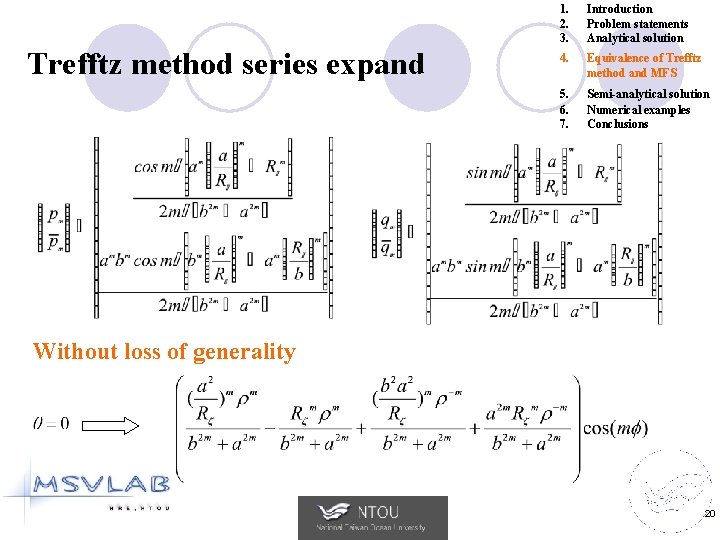
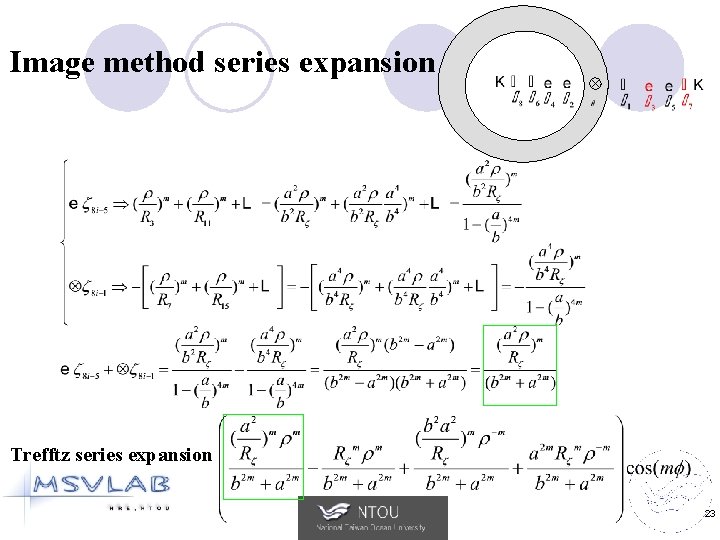
Trefftz method series expand 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions Without loss of generality 20

Image method series expansion Trefftz series expansion 21

Image method series expansion Trefftz series expansion 22

Image method series expansion Trefftz series expansion 23

Image method series expansion Trefftz series expansion 24

Equivalence of solutions derived by Trefftz method and MFS Trefftz method 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions MFS Equivalence addition theorem 25

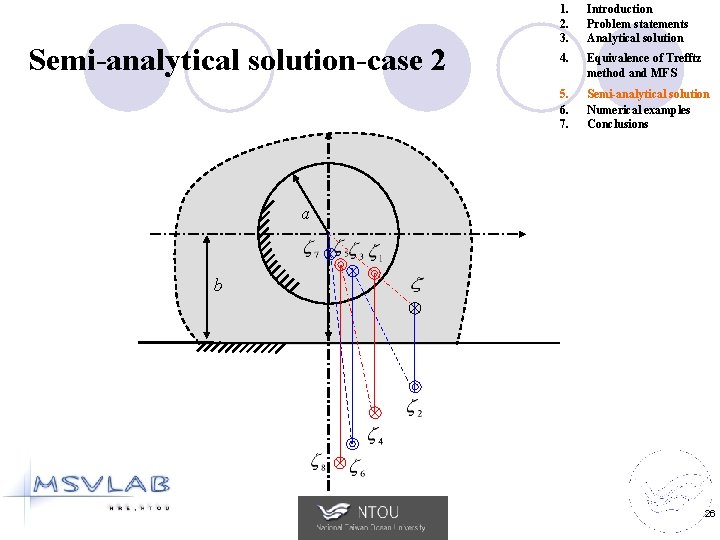
Semi-analytical solution-case 2 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions a b 26

MFS-Image group a 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions 27

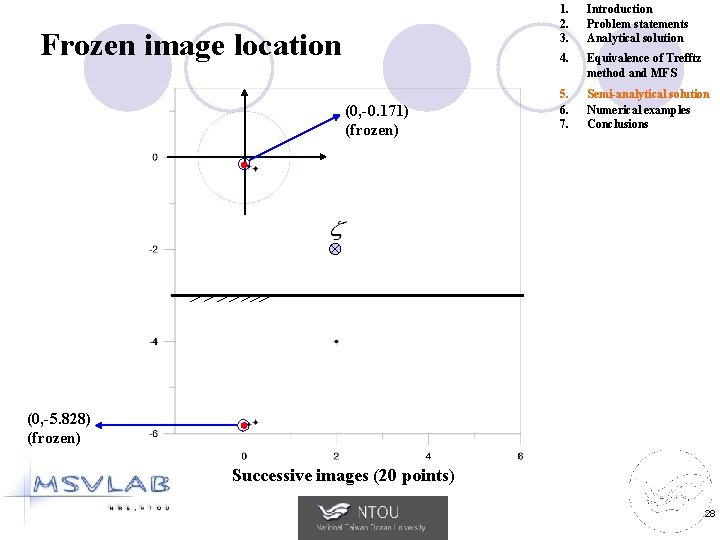
Frozen image location (0, -0. 171) (frozen) 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions (0, -5. 828) (frozen) Successive images (20 points) 28

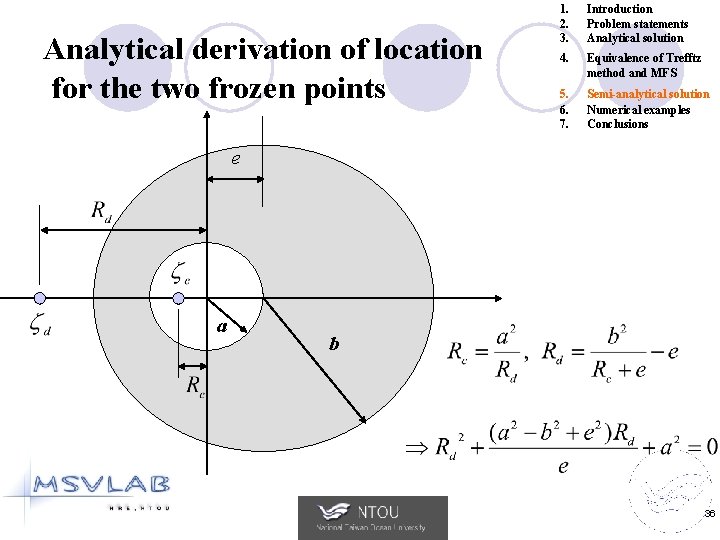
Analytical derivation of location for the two frozen points y a 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions x b (0. 171 & 5. 828) 29

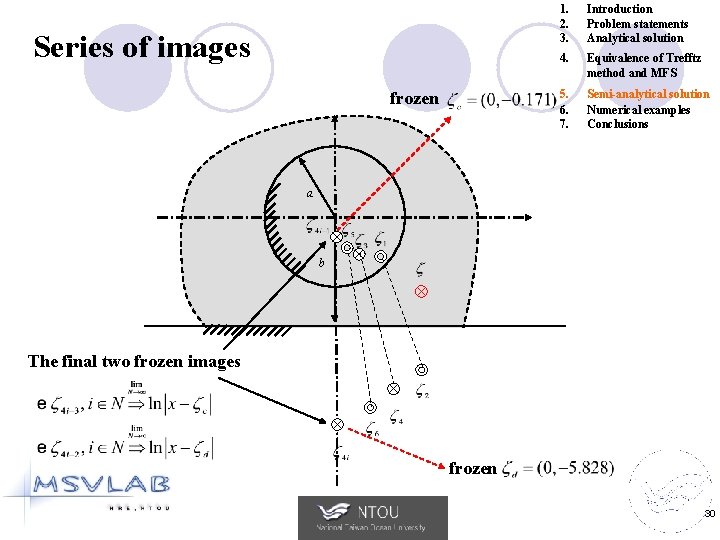
Series of images frozen 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions a b The final two frozen images frozen 30

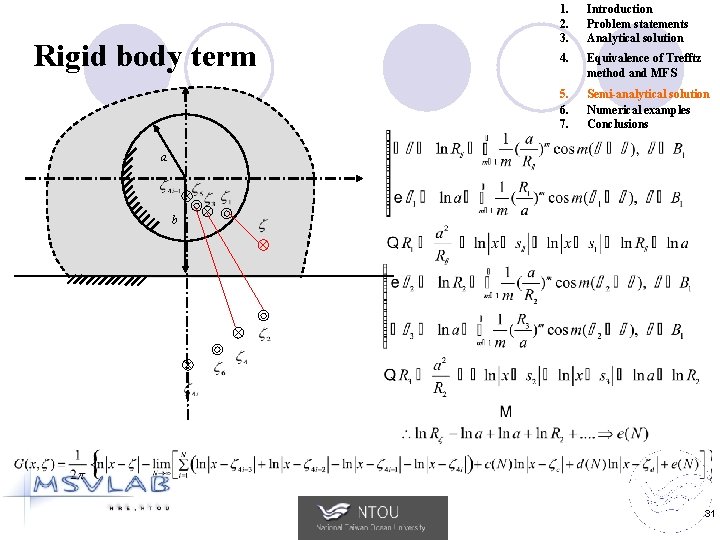
Rigid body term 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions a b 31

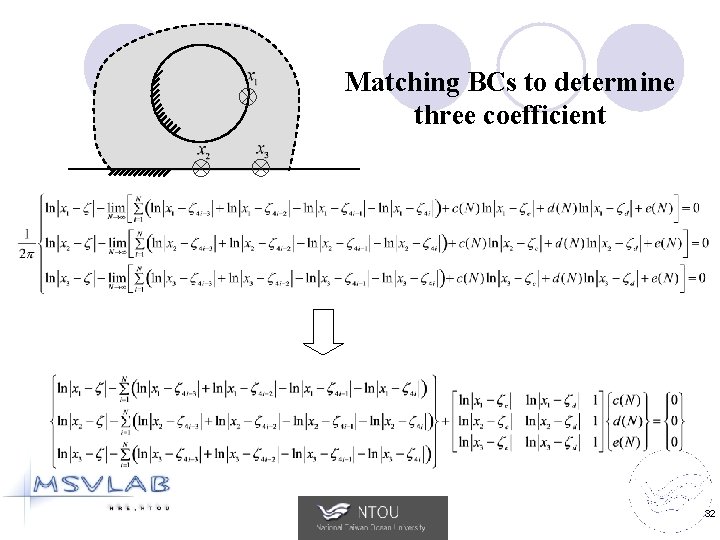
Matching BCs to determine three coefficient 32

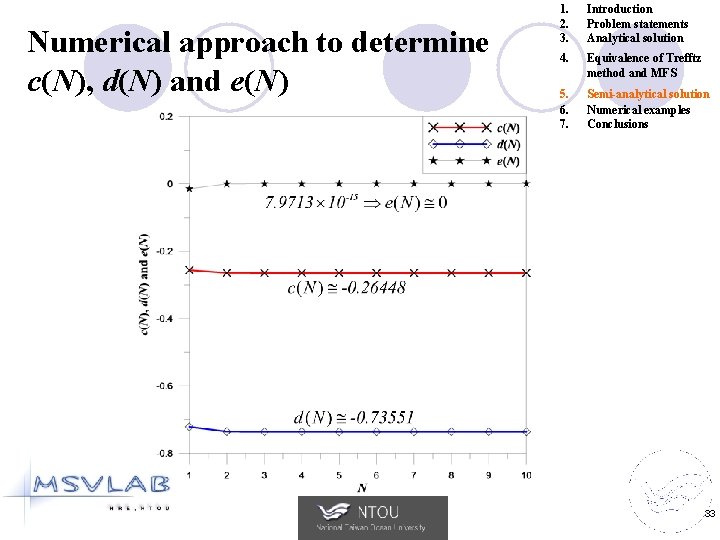
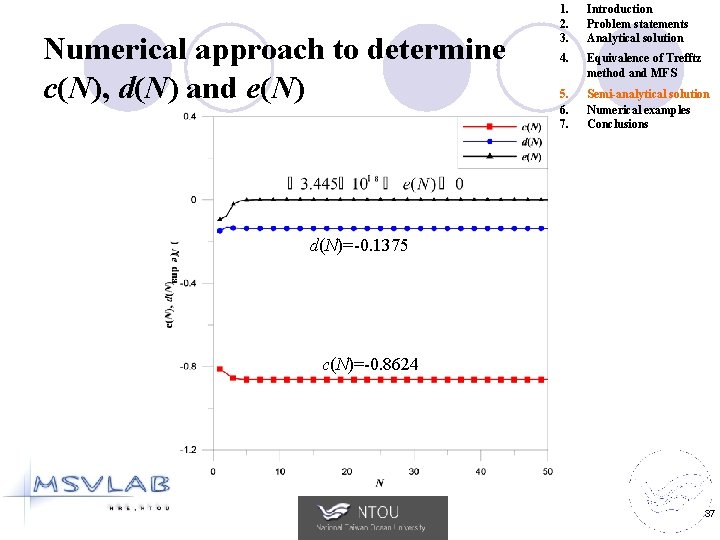
Numerical approach to determine c(N), d(N) and e(N) 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions 33

Semi-analytical solution-case 3 y 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions e x a u 2=0 b u 1=0 34

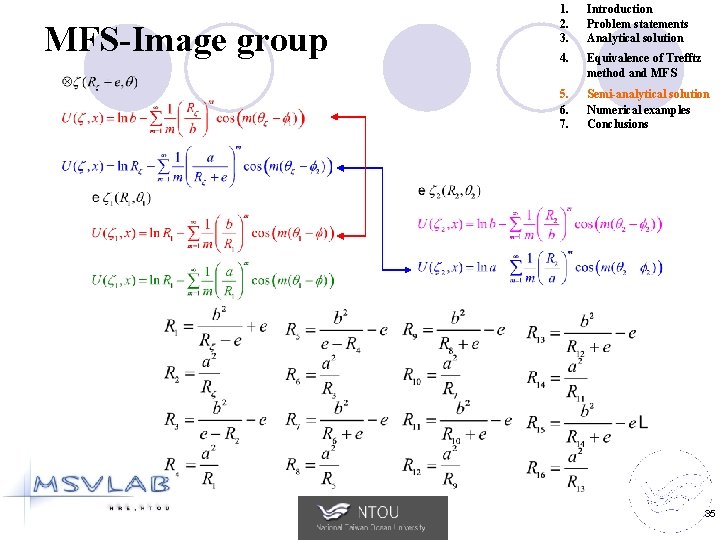
MFS-Image group 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions 35

Analytical derivation of location for the two frozen points 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions e a b 36

Numerical approach to determine c(N), d(N) and e(N) 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions d(N)=-0. 1375 c(N)=-0. 8624 37

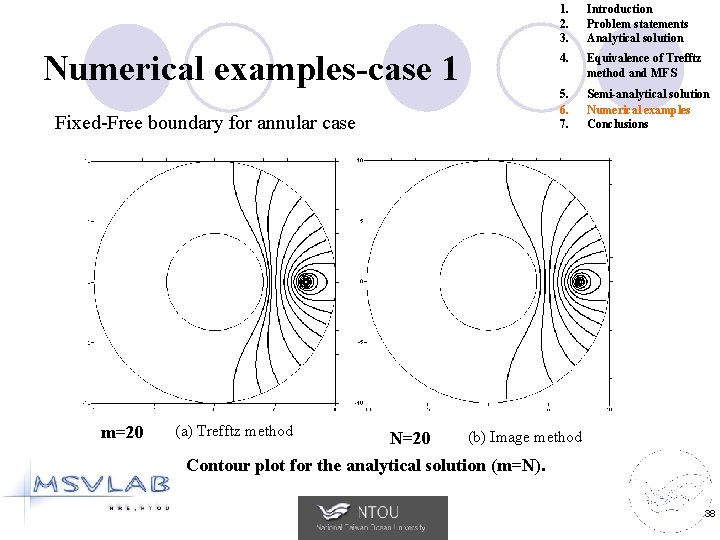
Numerical examples-case 1 Fixed-Free boundary for annular case m=20 (a) Trefftz method N=20 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions (b) Image method Contour plot for the analytical solution (m=N). 38

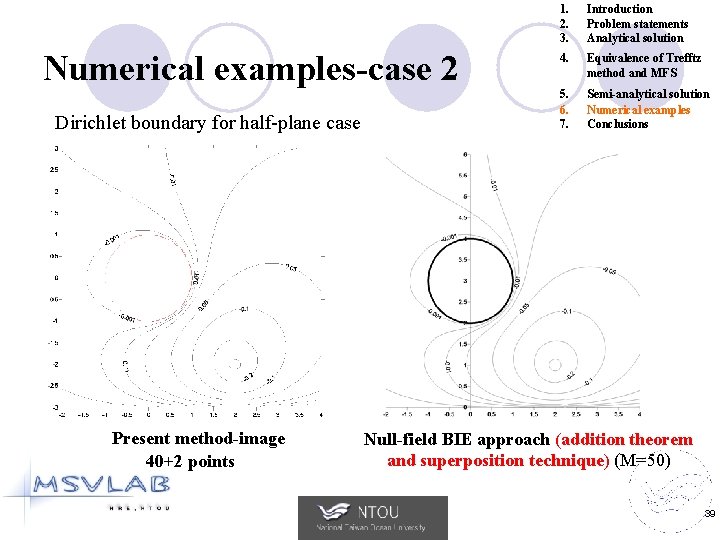
Numerical examples-case 2 Dirichlet boundary for half-plane case Present method-image 40+2 points 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions Null-field BIE approach (addition theorem and superposition technique) (M=50) 39

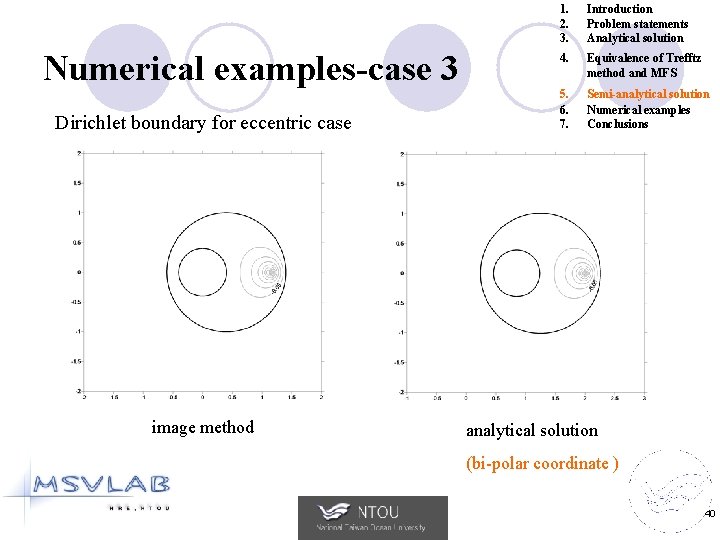
Numerical examples-case 3 Dirichlet boundary for eccentric case image method 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions analytical solution (bi-polar coordinate ) 40

Conclusions 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions The analytical solutions derived by the Trefftz method and MFS were proved to be mathematically equivalent for the annular Green’s functions. We can find final two frozen image points (one at origin and one at infinity). Their singularity strength can be determined numerically and analytically in a consistent manner. The image method can be seen as a special case for method of fundamental solution with optimal locations of sources. 41

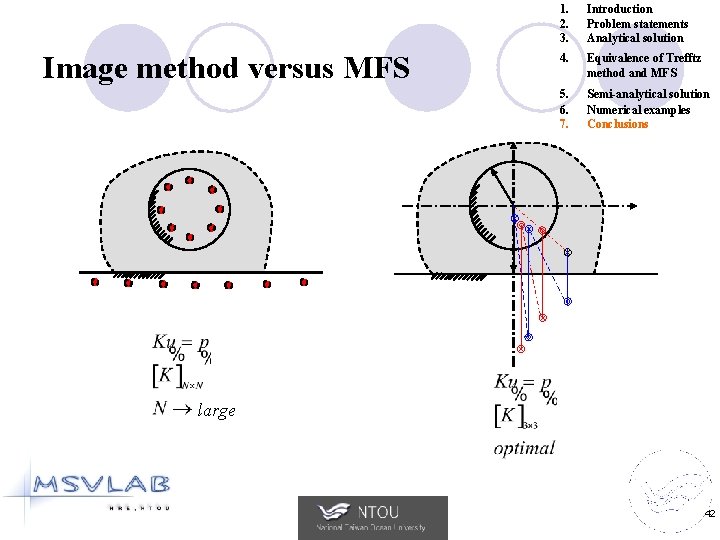
Image method versus MFS 1. 2. 3. Introduction Problem statements Analytical solution 4. Equivalence of Trefftz method and MFS 5. 6. 7. Semi-analytical solution Numerical examples Conclusions large 42

Thanks for your kind attentions You can get more information from our website http: //msvlab. hre. ntou. edu. tw/ October, 22, 2008 p. 43 垚淼 2008研討會