Image Denoising using Wavelet Thresholding Techniques Submitted by

Image Denoising using Wavelet Thresholding Techniques Submitted by Yang 9024553282

Introduction Image denoising: Removing unwanted noise in order to restore the original image. l Wavelet transform provides us with one of the methods for image denoising. l Wavelet transform, due to its excellent localization property, has rapidly become an indispensable signal and image processing tool for a variety of applications, including denoising and compression. l Wavelet denoising attempts to remove the noise present in the signal while preserving the signal characteristics, regardless of its frequency content. l

Introduction l It involves three steps: ¡a linear forward wavelet transform ¡ nonlinear thresholding step and ¡ a linear inverse wavelet transform l Methods Used ¡ Universal Thresholding ¡ Visu Shrink ¡ Sure Shrink ¡ Bayes Shrink

Wavelet Thresholding Wavelet thresholding (first proposed by Donoho) is a signal estimation technique that exploits the capabilities of wavelet transform for signal denoising. l It removes noise by killing coefficients that are insignificant relative to some threshold. l Researchers have developed various techniques for choosing denoising parameters and so far there is no “best” universal threshold determination technique. l Types l ¡ Universal or Global Thresholding l l ¡ Hard Soft Sub. Band Adaptive Thresholding

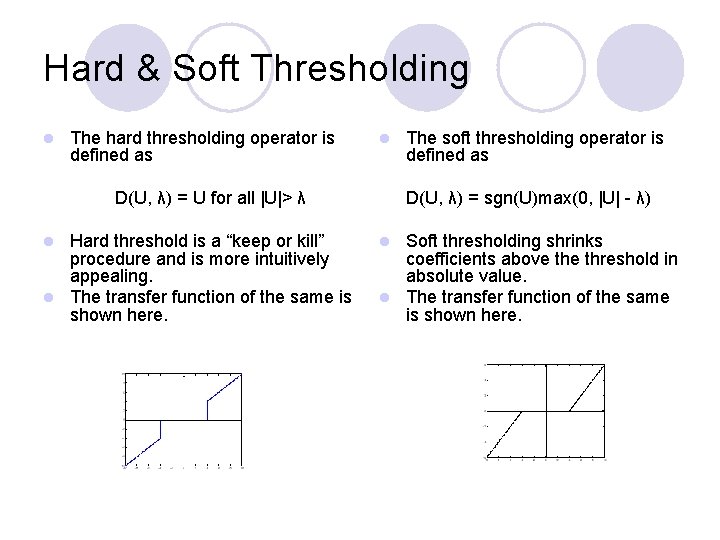
Hard & Soft Thresholding l The hard thresholding operator is defined as l D(U, λ) = U for all |U|> λ Hard threshold is a “keep or kill” procedure and is more intuitively appealing. l The transfer function of the same is shown here. l The soft thresholding operator is defined as D(U, λ) = sgn(U)max(0, |U| - λ) Soft thresholding shrinks coefficients above threshold in absolute value. l The transfer function of the same is shown here. l

Universal or Global Thresholding l The threshold (N being the signal length, σ being the noise variance) is well known in wavelet literature as the Universal threshold. l It is the optimal threshold in the asymptotic sense and minimizes the cost function of the difference between the function and the soft thresholded version of the same in the L 2 norm sense. l It is useful for obtain a starting value when nothing is known of the signal condition.

Results with Hard & Soft Thresholds (Universal thresholding)

Visu. Shrink l Visu. Shrink is thresholding by applying the Universal threshold proposed by Donoho and Johnstone. l This threshold is given by where σ is the noise variance and M is the number of pixels in the image. l For denoising images, Visu. Shrink is found to yield an overly smoothed estimate.

Results with Visu Shrink

SURE Shrink SUREShrink is a thresholding by applying subband adaptive threshold. l It is based on Stein’s Unbiased Estimator for Risk (SURE), a method for estimating the loss in an unbiased fashion. l Let wavelet coefficients in the jth subband be { Xi : i =1, …, d } l For the soft threshold estimator l we have l Select threshold t. S by

Bayes Shrink l Bayes. Shrink is an adaptive data-driven threshold for image denoising via wavelet soft-thresholding. l We assume generalized Gaussian distribution (GGD) for the wavelet coefficients in each detail subband. l We then try to find the threshold T which minimizes the Bayesian Risk.

Results with SURE & Bayes Shrink

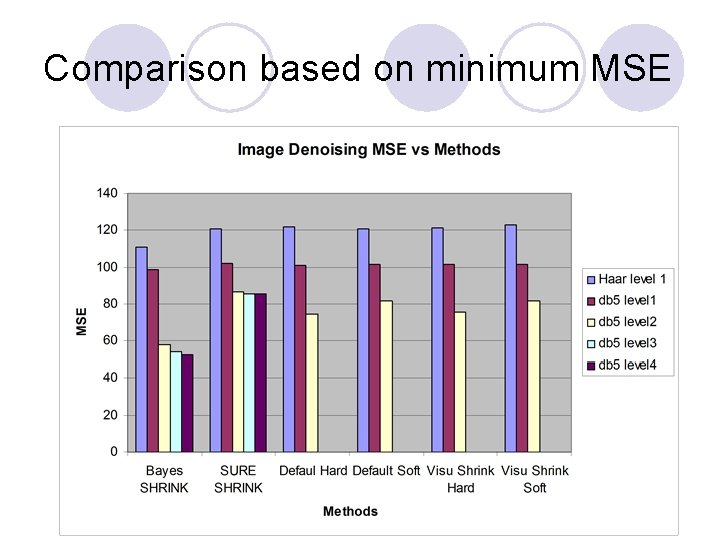
Comparison based on minimum MSE