Image classification by sparse coding Andrew Ng Feature

Image classification by sparse coding Andrew Ng

Feature learning problem • Given a 14 x 14 image patch x, can represent it using 196 real numbers. • Problem: Can we find a learn a better representation for this? Andrew Ng

Unsupervised feature learning Given a set of images, learn a better way to represent image than pixels. Andrew Ng

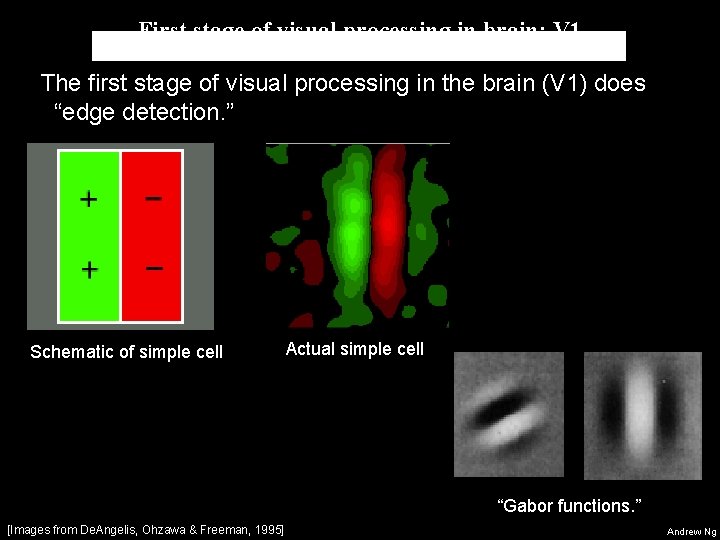
First stage of visual processing in brain: V 1 The first stage of visual processing in the brain (V 1) does “edge detection. ” Schematic of simple cell Actual simple cell “Gabor functions. ” [Images from De. Angelis, Ohzawa & Freeman, 1995] Andrew Ng

Learning an image representation Sparse coding (Olshausen & Field, 1996) Input: Images x(1), x(2), …, x(m) (each in Rn x n) Learn: Dictionary of bases 1, 2, …, k (also Rn x n), so that each input x can be approximately decomposed as: s. t. aj’s are mostly zero (“sparse”) Andrew Ng

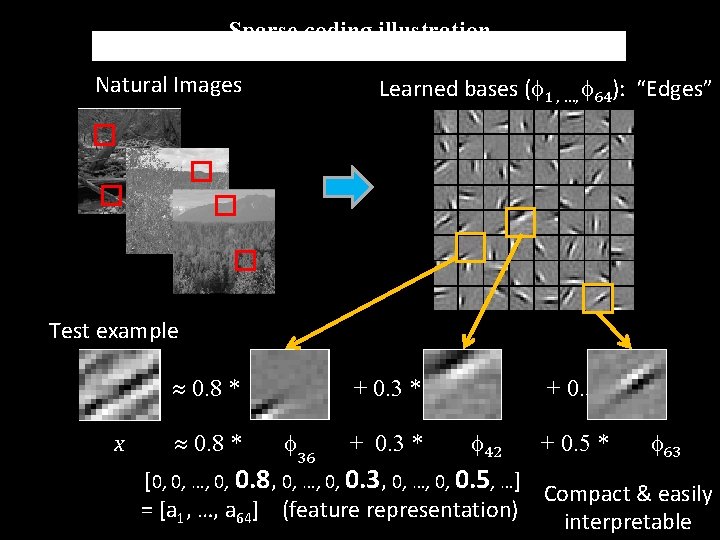
Sparse coding illustration Natural Images Learned bases ( 1 , …, 64): “Edges” Test example » 0. 8 * x » 0. 8 * + 0. 3 * 36 + 0. 3 * + 0. 5 * 42 + 0. 5 * 63 [0, 0, …, 0, 0. 8, 0, …, 0, 0. 3, 0, …, 0, 0. 5, …] Compact & easily = [a 1, …, a 64] (feature representation) interpretable Andrew Ng

More examples » 0. 6 * + 0. 8 * 15 + 0. 4 * 28 37 Represent as: [0, 0, …, 0, 0. 6, 0, …, 0, 0. 8, 0, …, 0, 0. 4, …] » 1. 3 * + 0. 9 * 5 + 0. 3 * 18 Represent as: [0, 0, …, 0, 1. 3, 0, …, 0, 0. 9, 0, …, 0, 0. 3, …] 29 • Method hypothesizes that edge-like patches are the most “basic” elements of a scene, and represents an image in terms of the edges that appear in it. • Use to obtain a more compact, higher-level representation of the scene than pixels. Andrew Ng

Digression: Sparse coding applied to audio [Evan Smith & Mike Lewicki, 2006] Andrew Ng

Sparse coding details Input: Images x(1), x(2), …, x(m) (each in Rn x n) L 1 sparsity term (causes most s to be 0) Alternating minimization: Alternately minimize with respect to i‘s (easy) and a’s (harder). Andrew Ng

Solving for bases Early versions of sparse coding were used to learn about this many bases: 32 learned bases How to scale this algorithm up? Andrew Ng

Sparse coding details Input: Images x(1), x(2), …, x(m) (each in Rn x n) L 1 sparsity term Alternating minimization: Alternately minimize with respect to i‘s (easy) and a’s (harder). Andrew Ng

Feature sign search (solve for ai’s) Goal: Minimize objective with respect to ai’s. • Simplified example: • Suppose I tell you: • Problem simplifies to: • This is a quadratic function of the ai’s. Can be solved efficiently in closed form. • Algorithm: • Repeatedly guess sign (+, - or 0) of each of the ai’s. • Solve for ai’s in closed form. Refine guess for signs. Andrew Ng

The feature-sign search algorithm: Visualization Current guess: Starting from zero (default) Andrew Ng

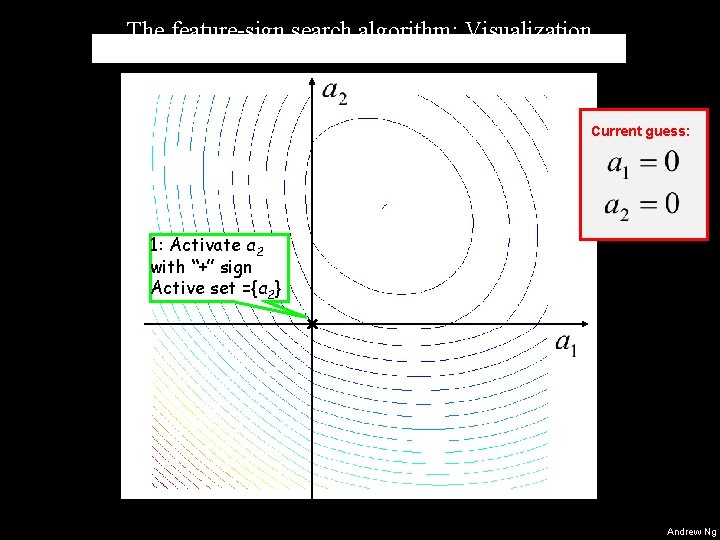
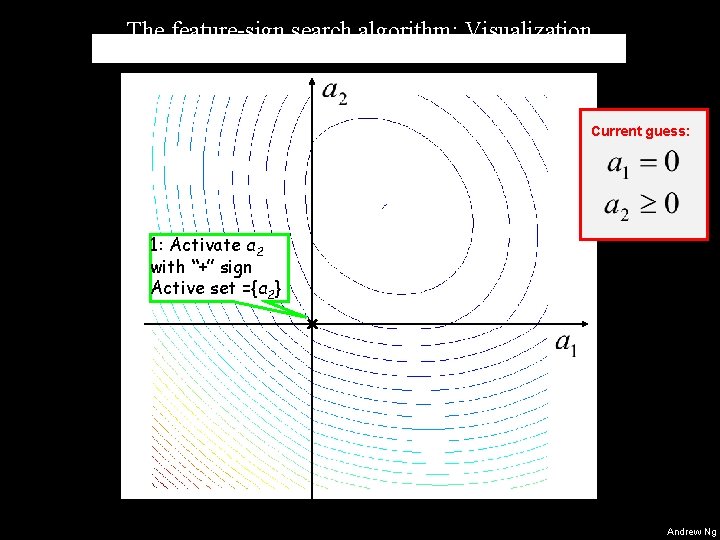
The feature-sign search algorithm: Visualization Current guess: 1: Activate a 2 with “+” sign Active set ={a 2} Starting from zero (default) Andrew Ng

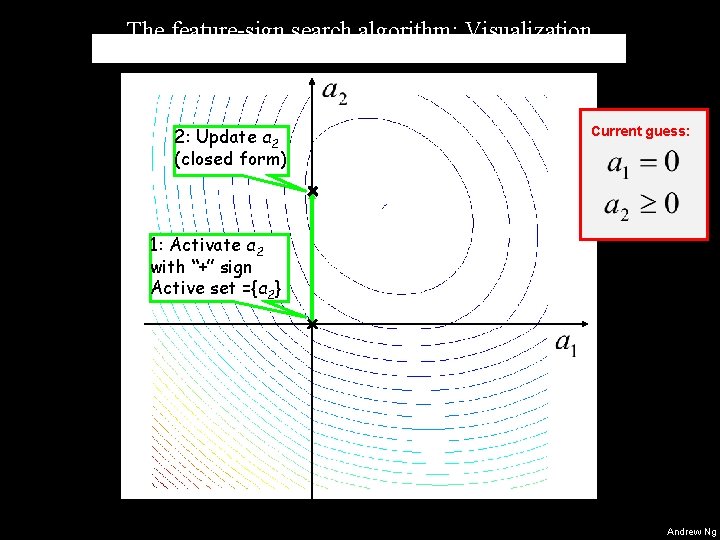
The feature-sign search algorithm: Visualization 2: Update a 2 (closed form) Current guess: 1: Activate a 2 with “+” sign Active set ={a 2} Starting from zero (default) Andrew Ng

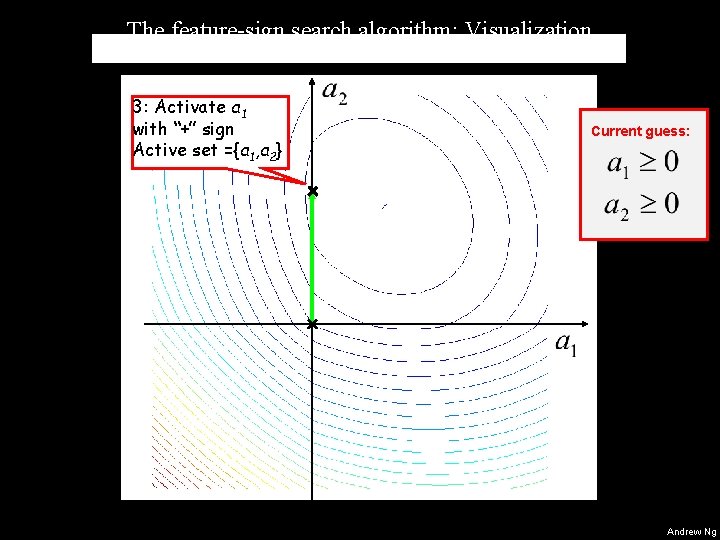
The feature-sign search algorithm: Visualization 3: Activate a 1 with “+” sign Active set ={a 1, a 2} Current guess: Starting from zero (default) Andrew Ng

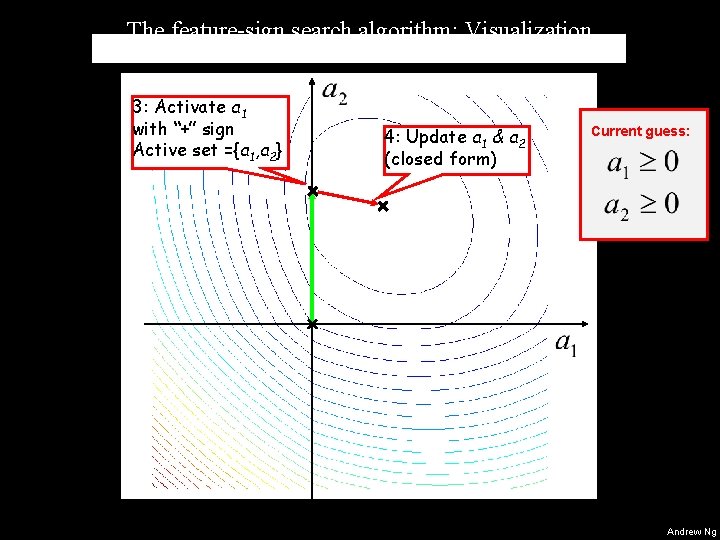
The feature-sign search algorithm: Visualization 3: Activate a 1 with “+” sign Active set ={a 1, a 2} 4: Update a 1 & a 2 (closed form) Current guess: Starting from zero (default) Andrew Ng

Before feature sign search 32 learned bases Andrew Ng

With feature signed search Andrew Ng

Training time Recap of sparse coding for feature learning Input: Images x(1), x(2), …, x(m) (each in Rn x n) Learn: Dictionary of bases 1, 2, …, k (also Rn x n). Test time Input: Novel image x (in Rn x n) and previously learned i’s. Output: Representation [a 1, a 2, …, ak] of image x. » 0. 8 * + 0. 3 * + 0. 5 * x » 0. 8 * 36 + 0. 3 * 42 + 0. 5 * Represent as: [0, 0, …, 0, 0. 8, 0, …, 0, 0. 3, 0, …, 0, 0. 5, …] 63 Andrew Ng

Sparse coding recap » 0. 8 * + 0. 3 * + 0. 5 * [0, 0, …, 0, 0. 8, 0, …, 0, 0. 3, 0, …, 0, 0. 5, …] Much better than pixel representation. But still not competitive with SIFT, etc. Three ways to make it competitive: • Combine this with SIFT. • Advanced versions of sparse coding (LCC). • Deep learning. Andrew Ng

Combining sparse coding with SIFT Input: Images x(1), x(2), …, x(m) (each in Rn x n) SIFT descriptors x(1), x(2), …, x(m) (each in R 128) Learn: Dictionary of bases 1, 2, …, k (also Rn x n). R 128. Test time: Given novel SIFT descriptor, x (in R 128), represent as Andrew Ng

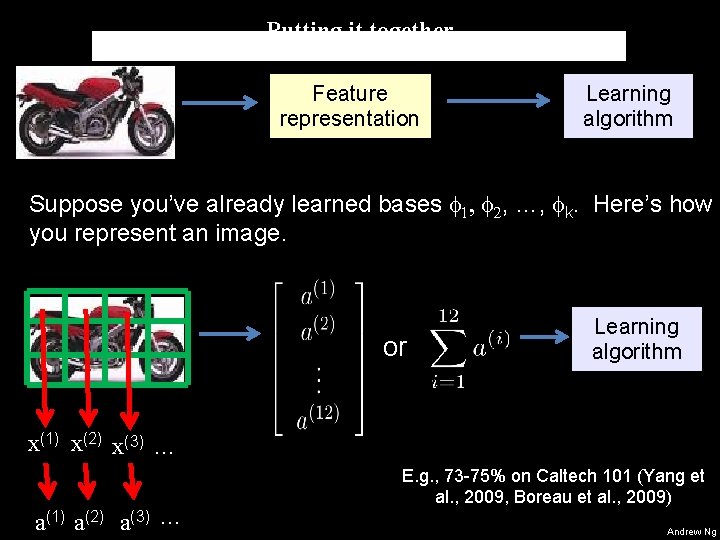
Putting it together Feature representation Learning algorithm Suppose you’ve already learned bases 1, 2, …, k. Here’s how you represent an image. or Learning algorithm x(1) x(2) x(3) … a(1) a(2) a(3) … E. g. , 73 -75% on Caltech 101 (Yang et al. , 2009, Boreau et al. , 2009) Andrew Ng

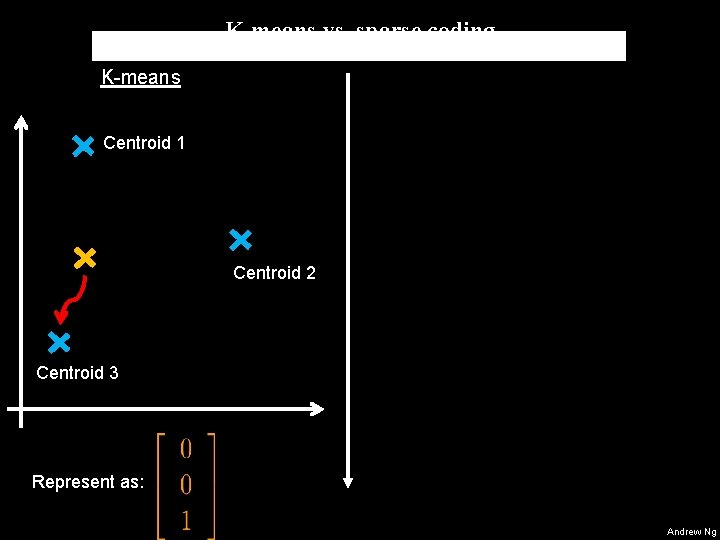
K-means vs. sparse coding K-means Centroid 1 Centroid 2 Centroid 3 Represent as: Andrew Ng

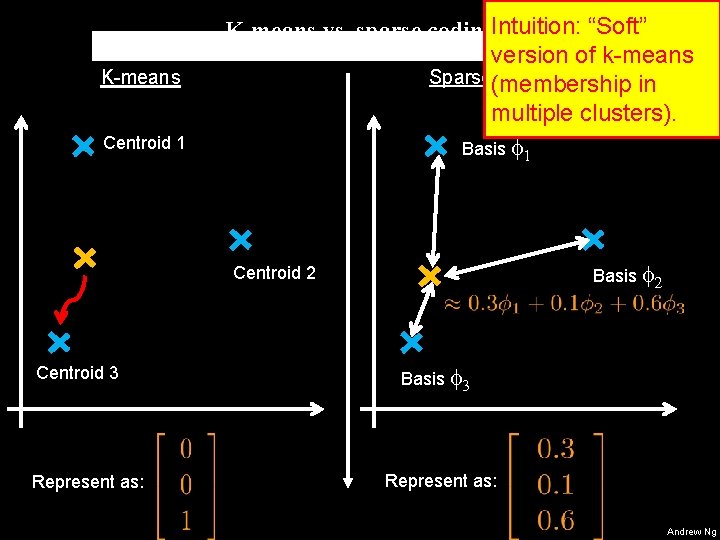
K-means Centroid 1 K-means vs. sparse coding. Intuition: “Soft” version of k-means Sparse(membership coding in multiple clusters). Basis 1 Basis 2 Centroid 3 Represent as: Basis 3 Represent as: Andrew Ng

K-means vs. sparse coding Rule of thumb: Whenever using kmeans to get a dictionary, if you replace it with sparse coding it’ll often work better. Andrew Ng