Image by M Boran Dublin The Physics of

Image by M. Boran (Dublin) The Physics of Foams Simon Cox

Outline • Foam structure – rules and description • Dynamics Prototypes for many other systems: metallic grain growth, biological organisms, crystal structure, emulsions, …

Motivation Many applications of industrial importance: • Oil recovery • Fire-fighting • Ore separation • Industrial cleaning • Vehicle manufacture • Food products

Dynamic phenomena in Foams Must first understand the foam’s structure

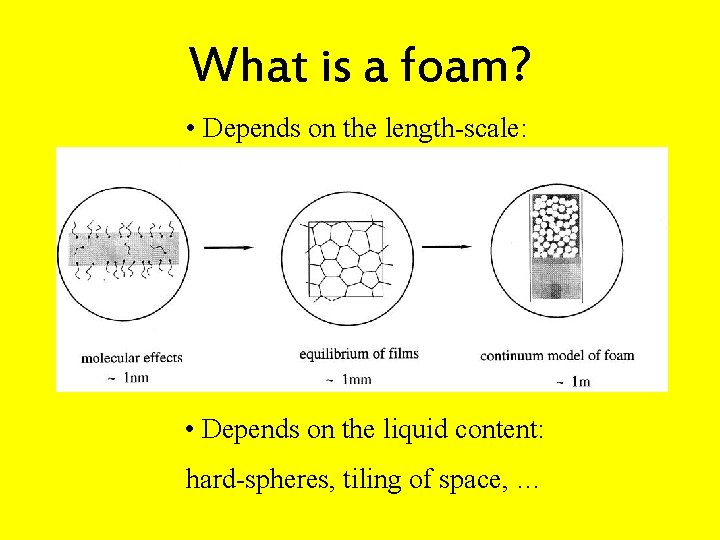
What is a foam? • Depends on the length-scale: • Depends on the liquid content: hard-spheres, tiling of space, …

How are foams made? from Weaire & Hutzler, The Physics of Foams (Oxford)

Single bubble Soap film minimizes its energy = surface area Least area way to enclose a given volume is a sphere. Isoperimetric problem (known to Greeks, proven in 19 th century)

Laplace-Young Law (200 years old) Mean curvature C of each film is balanced by the pressure difference across it: Coefficient of proportionality is the surface tension Soap films have constant mean curvature

Plateau’s Rules Minimization of area gives geometrical constraints (“observation” = Plateau, proof = Taylor): • Three (and only three) films meet, at 120°, in a Plateau border • Plateau borders always meet symmetrically in fours (Maraldi angle).

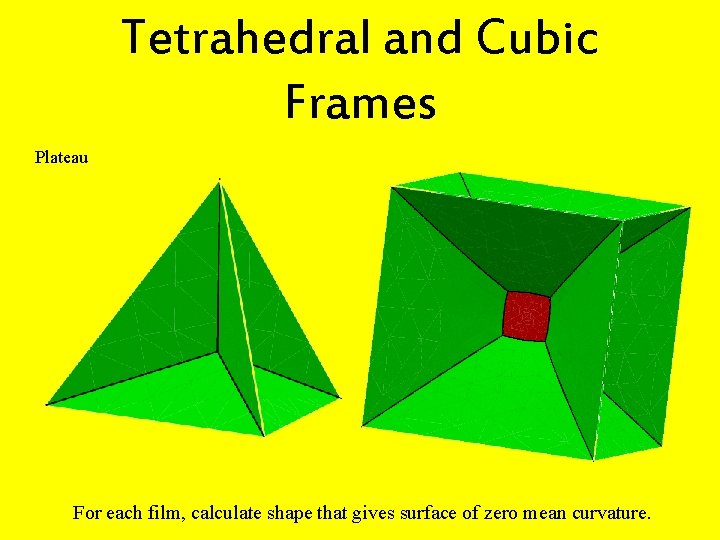
Tetrahedral and Cubic Frames Plateau For each film, calculate shape that gives surface of zero mean curvature.

Bubbles in wire frames D’Arcy Thompson

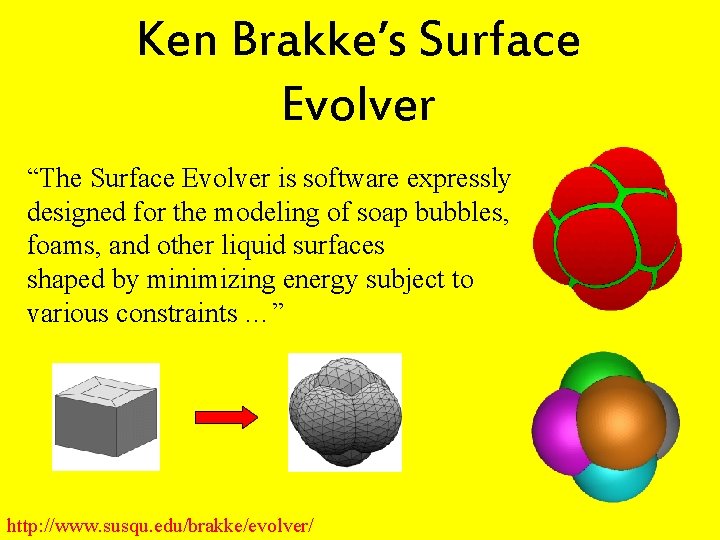
Ken Brakke’s Surface Evolver “The Surface Evolver is software expressly designed for the modeling of soap bubbles, foams, and other liquid surfaces shaped by minimizing energy subject to various constraints …” http: //www. susqu. edu/brakke/evolver/

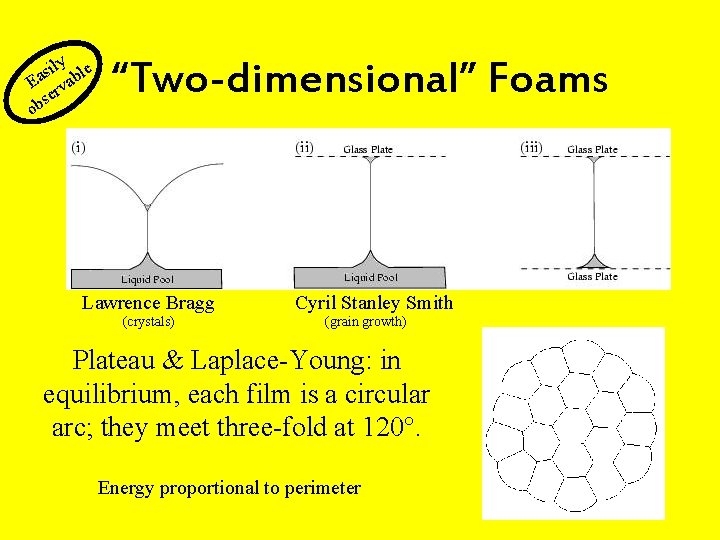
ly le i s Ea rvab se b o “Two-dimensional” Foams Lawrence Bragg (crystals) Cyril Stanley Smith (grain growth) Plateau & Laplace-Young: in equilibrium, each film is a circular arc; they meet three-fold at 120°. Energy proportional to perimeter

Topological changes • T 1: neighbour swapping (reduces perimeter) • T 2: bubble disappearance

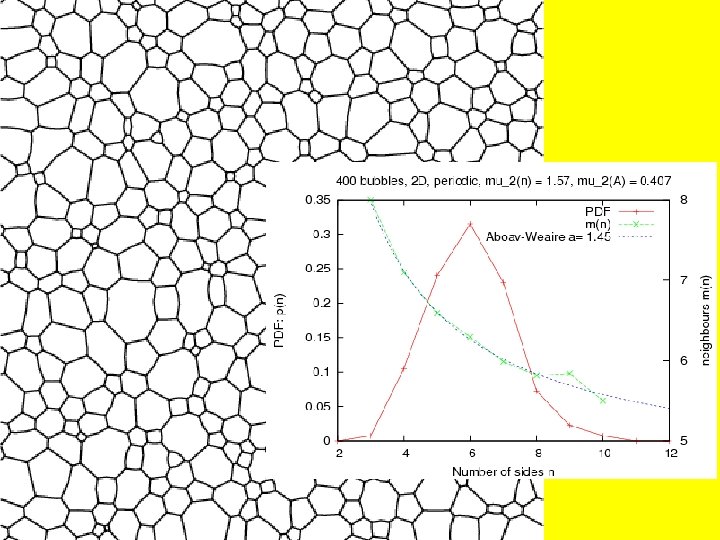
Describing 2 D foam structure • Euler’s Law: • Second moment of number of edges per bubble:

Describing foam structure Aboav-Weaire Law: where m(n) is the average number of sides of cells with n-sided neighbours. Applied (successfully) to many natural and artificial cellular structures. What is a?

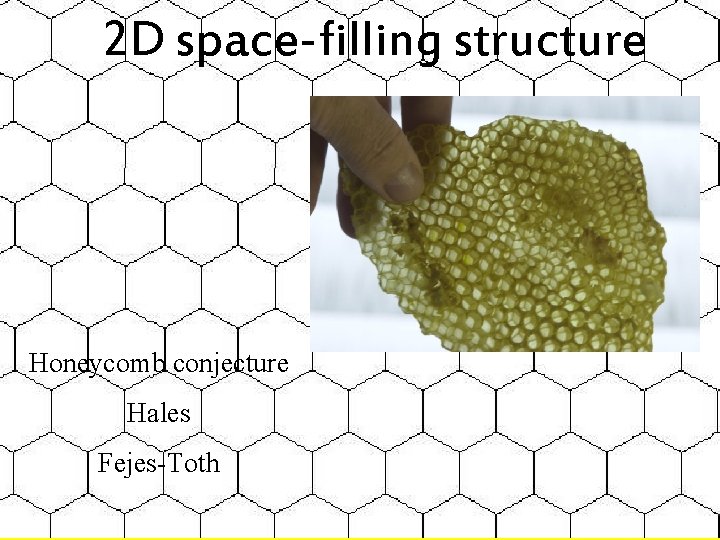
2 D space-filling structure Honeycomb conjecture Hales Fejes-Toth

Finite 2 D clusters Find minimal energy cluster for N bubbles. Proofs for N=2 and 3. Morgan et al. Wichiramala How many possibilities are there for each N?

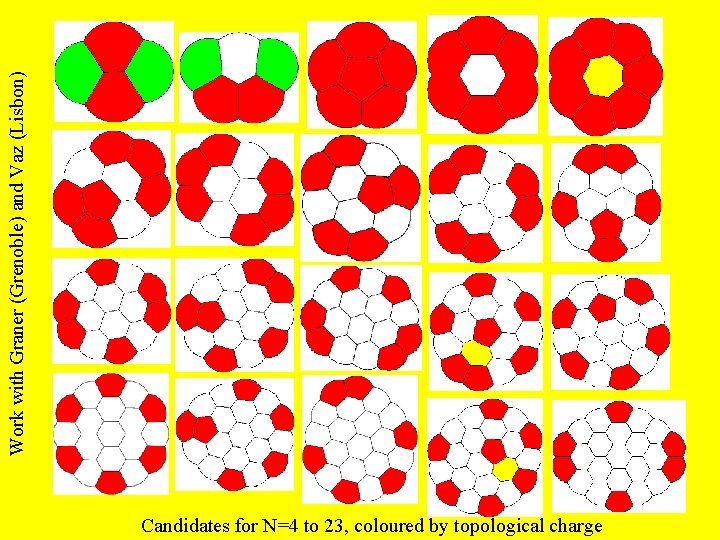
Work with Graner (Grenoble) and Vaz (Lisbon) Candidates for N=4 to 23, coloured by topological charge

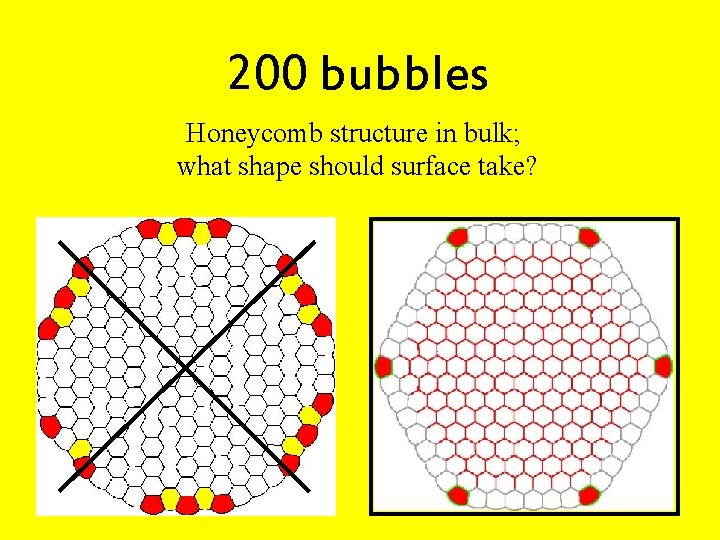
200 bubbles Honeycomb structure in bulk; what shape should surface take?

Tarnai (Budapest) Lotus flowers Seed heads represented by perimeter minima for bubbles inside a circular constraint? Also work on fly eyes (Carthew) and sea urchins (Raup, D’Arcy Thompson)

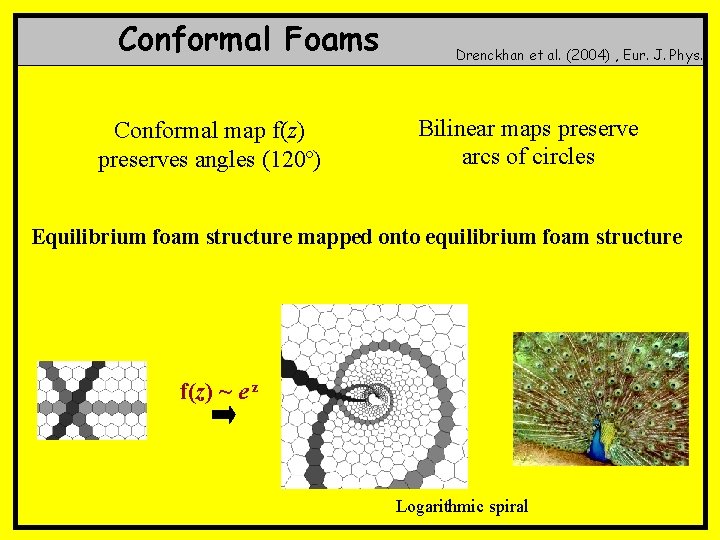
Conformal Foams Conformal map f(z) preserves angles (120º) Drenckhan et al. (2004) , Eur. J. Phys. Bilinear maps preserve arcs of circles Equilibrium foam structure mapped onto equilibrium foam structure f(z) ~ e z Logarithmic spiral

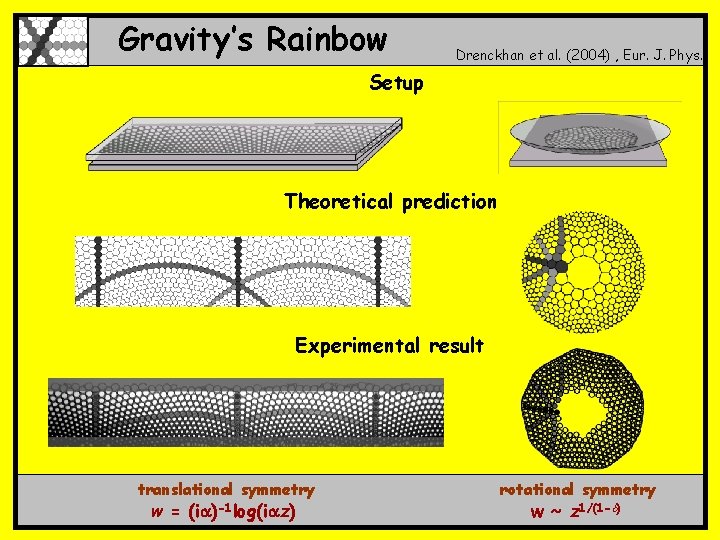
Gravity’s Rainbow Drenckhan et al. (2004) , Eur. J. Phys. Setup Theoretical prediction Experimental result translational symmetry w = (ia)-1 log(iaz) rotational symmetry w ~ z 1/(1 - )

Ordered Foams in 3 D ratio: bubble diameter / tube diameter gas - pressure; nozzle diameter (Elias, Hutzler, Drenckhan)

Description of 3 D bulk structure • Topological changes similar, but more possibilities. • (Euler, Coxeter, Kusner) restricts possible regular structures. • Second moment: • Sauter mean radius: • Aboav-Weaire Law (polydisperse)

3 D space-filling structure Polyhedral cells with curved faces packed together to fill space. What’s the best arrangement? (Kelvin problem) Euler & Plateau: need structure with average of 13. 39 faces and 5. 1 edges per face 14 “delicately curved” faces (6 squares, 8 hexagons) <E>=5. 14 See Weaire (ed), The Kelvin Problem (1994) Kelvin’s Bedspring (tetrakaidecahedron)

Weaire-Phelan structure Kelvin’s candidate structure reigned for 100 years WP is based on A 15 TCP structure/ β-tungsten clathrate <F>=13. 5, <E>=5. 111 0. 3% lower in surface area 2 pentagonal dodecahedra 6 Goldberg 14 -hedra Swimming pool for 2008 Beijing Olympics (ARUP) Surface Evolver

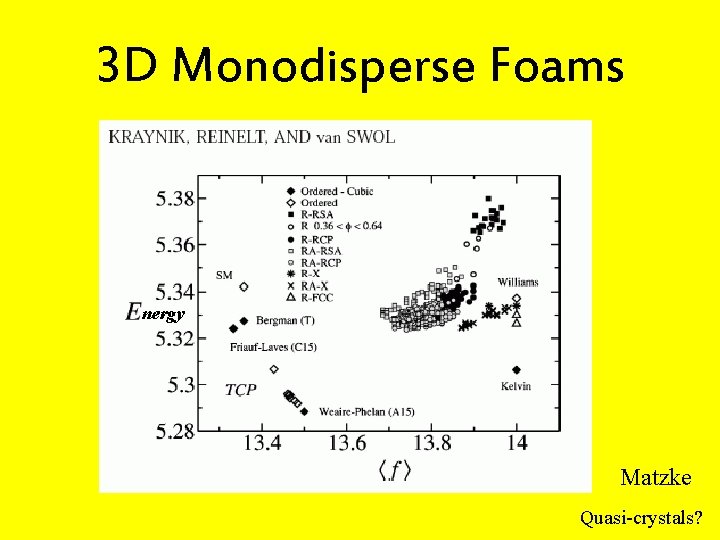
3 D Monodisperse Foams nergy Matzke Quasi-crystals?

Finite 3 D clusters J. M. Sullivan (Berlin) Find minimal energy cluster for N bubbles. Must eliminate strange possibilities: Proof that “obvious” answer is the right one for N=2 bubbles in 3 D, but for no greater N.

27 bubbles surround one other Finite 3 D clusters DWT Central bubble from 123 bubble cluster

Coarsening Drainage Rheology Graner, Cloetens (Grenoble) Dynamics

Coarsening Gas diffuses across soap films due to pressure differences between bubbles. Von Neumann’s Law - rate of change of area due to gas diffusion depends only upon number of sides: Only in 2 D. Also applies to grain growth. T 1 s and T 2 s

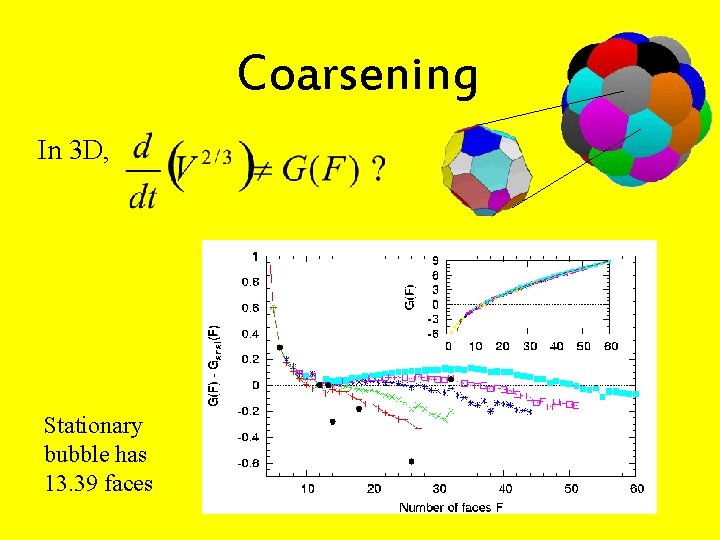
Coarsening In 3 D, Stationary bubble has 13. 39 faces

Foam Rheology • Elastic solids at low strain • Behave as plastic solids as strain increases • Liquid-like at very high strain Exploit bubble-scale structure (Plateau’s laws) to predict and model the rheological response of foams. Energy dissipated through topological changes (even in limit of zero shear-rate). Properties scale with average bubble area.

J. A. Glazier (Indiana) 2 D contraction flow

Experiment by G. Debregeas (Paris), PRL ‘ 01 Couette Shear (Experiment) Shear banding? Localization? Much faster than real-time. cf Lauridsen et al. PRL 2002

Couette Shear Simulations Quasistatic: Include viscous drag on bounding plates:

Outlook This apparently complex two-phase material has a well-defined local structure. This structure allows progress in predicting the dynamic properties of foams The Voronoi construction provides a useful starting condition (e. g. for simulations and special cases) but neglects the all-important curvature.