Illustrative Basic Examples demonstrating the importance of models

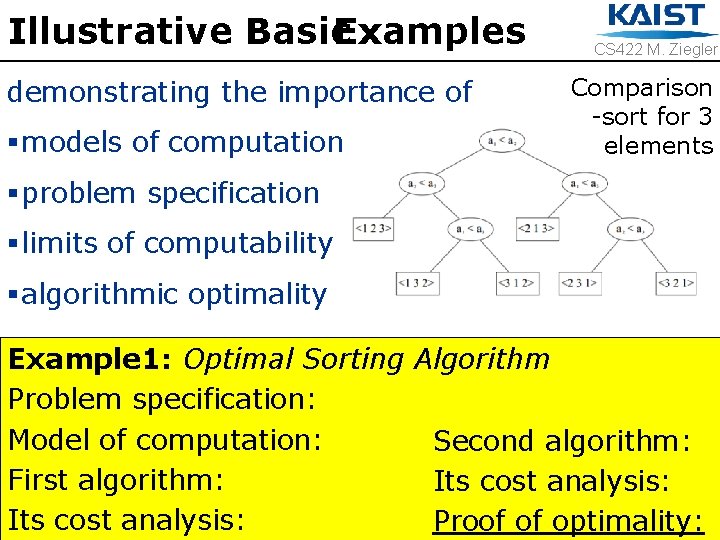
Illustrative Basic Examples demonstrating the importance of § models of computation CS 422 M. Ziegler Comparison -sort for 3 elements § problem specification § limits of computability § algorithmic optimality Example 1: Optimal Sorting Algorithm Problem specification: Model of computation: Second algorithm: First algorithm: Its cost analysis: Proof of optimality:

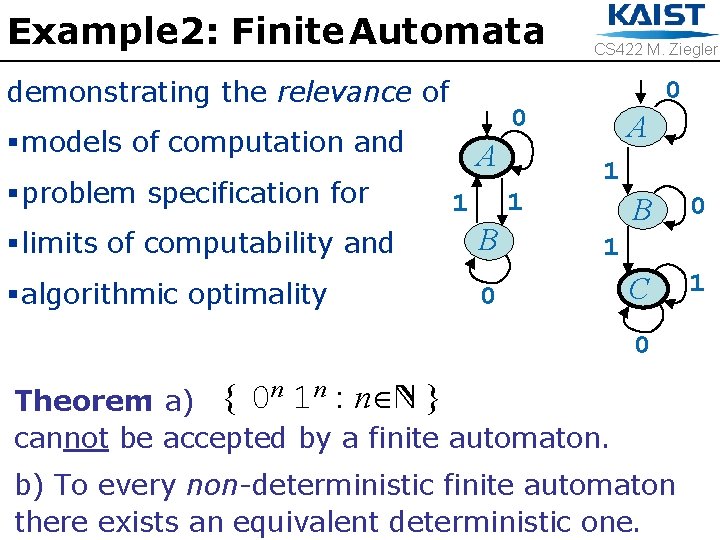
Example 2: Finite Automata demonstrating the relevance of 0 0 § models of computation and § problem specification for CS 422 M. Ziegler A 1 1 § limits of computability and B § algorithmic optimality 0 A 1 B 0 C 1 1 0 Theorem: a) { 0 n 1 n : n N } cannot be accepted by a finite automaton. b) To every non-deterministic finite automaton there exists an equivalent deterministic one.

Example 3: Algebraic. Complexity CS 422 M. Ziegler n log 2 n · 10 s n·log n sec n² msec n³ μsec 2 n nsec 10 33 sec 0. 1 sec 1 msec 100 1 min 10 sec 1 sec 40 Mrd. Y 1000 1. 5 min 3 h 17 min 10 000 2 min 1. 5 days 1 day 11 days 100 000 2. 5 min 19 days 4 months 32 years Warmup. Problem: Fix n N. Given x, calculate xn. • Naïve algorithm: n-1 multiplications k 2 4 8 2 • Improve: Calculate x , x , …, x for k: = log 2 n j 2 Then multiply powers x with bj=1, where n=b 0+2 b 1+4 b 2+…+2 kbk is the binary expansion. • Asymptot. optimality: Each multiplication at most doubles the degree of the intermediate results; so computing xn requires at least log 2 n of them.

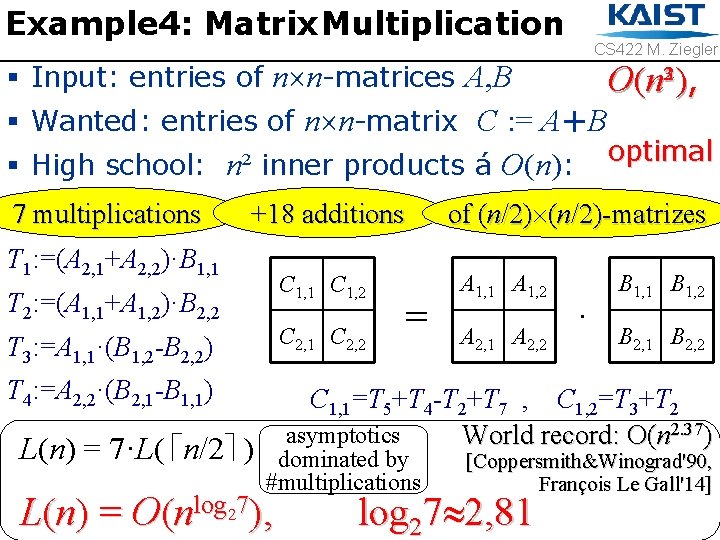
Example Matrix. Addition Multiplication Example 4: Matrix CS 422 M. Ziegler § Input: entries of n n-matrices A, B § Wanted: entries of n n-matrix C : = A+ ·B § High school: n² inner products á O(n): 7 multiplications T 1: =(A 2, 1+A 2, 2)·B 1, 1 T 2: =(A 1, 1+A 1, 2)·B 2, 2 T 3: =A 1, 1·(B 1, 2 -B 2, 2) +18 additions C 1, 1 C 1, 2 C 2, 1 C 2, 2 = O(n²) ³), optimal of (n/2)-matrizes A 1, 1 A 1, 2 A 2, 1 A 2, 2 T 4: =A 2, 2·(B 2, 1 -B 1, 1) · B 1, 1 B 1, 2 B 2, 1 B 2, 2 C 1, 1=T 5+T 4 -T 2+T 7 , C 1, 2=T 3+T 2 T 5: =(A 1, 1+A 2, 2)·(B 1, 1+B 2, 2)asymptotics World record: O(n 2. 37) C 2, 1=T C 2, 2=T 5 -T 1+T 3+T 6 L(n) = 7·L( n/2 ) +dominated 18·(n/2)² by 1+T 4, [Coppersmith&Winograd'90, T 6: =(A 2, 1 -A 1, 1)·(B 1, 1+B 1, 2#multiplications ) François Le Gall'14] log 27), L ( n ) = O ( n T 7: =(A 1, 2 -A 2, 2)·(B 2, 1+B 2, 2) log 27 2, 81

Alan M. Turing 1941 1936 CS 422 M. Ziegler • first scientific calculations on digital computers • What are its fundamental limitations? decision + • Uncountably many P N A B' problem B x B' A • but countably many B' 'algorithms' • Undecidable Halting Problem H : No algorithm B can always correctly answer the following question simulator /interpreter B? Given A, x , does algorithm A terminate on input x? contradiction: B' that, Proof by contradiction : Consider • Logicians Tarski, Alonzo Churchalgorithm (Ph. D advisor) upon a positive on input A, executes on A, A and, • Kurt Gödel (1931): BThere exist arithmetical answer , loops infinitely. How B' behave on B' statements which are true butdoes cannot be proven so. ?

Summaryof § 1 CS 422 M. Ziegler Theory of Computation § considers mathematical models of computers, § explores their capabilities and limitations § as well as optimal asymptotic algorithmic cost § for fully-specified computational problems. We have seen basic examples: § comparison-based branching trees § finite automata § algebraic unit-cost model (power, matrix mult) § some (unspecific/generic) programming system