IL PERIODO DELLE FUNZIONI GONIOMETRICHE Il grafico della

IL PERIODO DELLE FUNZIONI GONIOMETRICHE

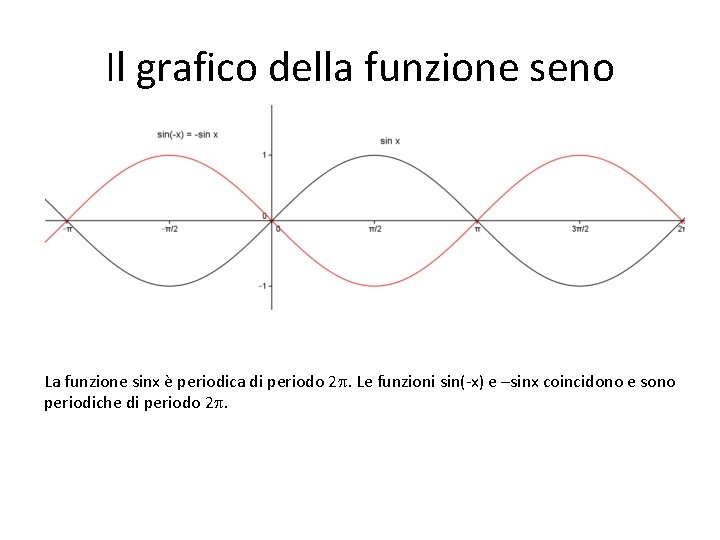
Il grafico della funzione seno La funzione sinx è periodica di periodo 2. Le funzioni sin(-x) e –sinx coincidono e sono periodiche di periodo 2.

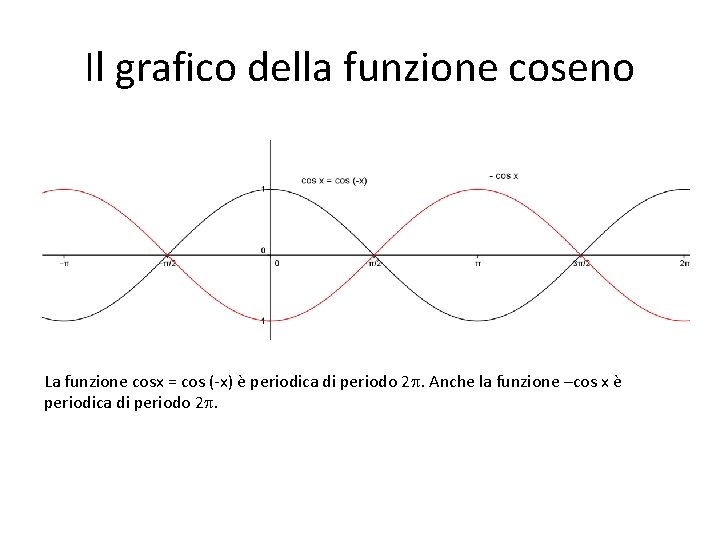
Il grafico della funzione coseno La funzione cosx = cos (-x) è periodica di periodo 2. Anche la funzione –cos x è periodica di periodo 2.

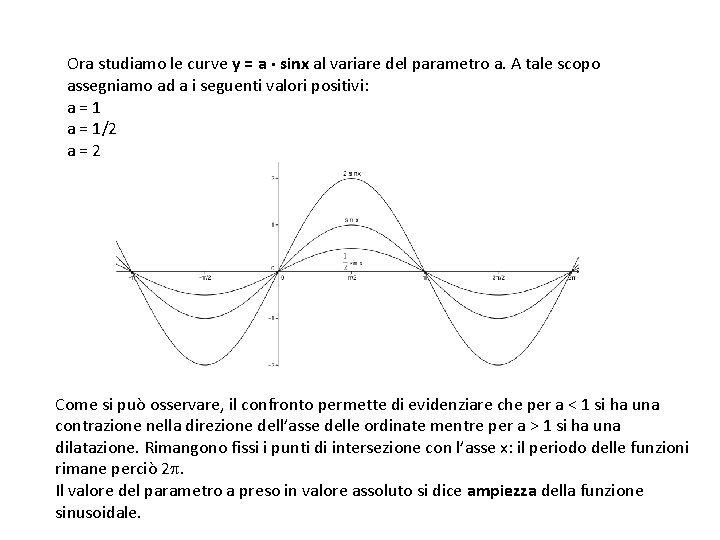
Ora studiamo le curve y = a ⋅ sinx al variare del parametro a. A tale scopo assegniamo ad a i seguenti valori positivi: a = 1/2 a = 2 Come si può osservare, il confronto permette di evidenziare che per a < 1 si ha una contrazione nella direzione dell’asse delle ordinate mentre per a > 1 si ha una dilatazione. Rimangono fissi i punti di intersezione con l’asse x: il periodo delle funzioni rimane perciò 2. Il valore del parametro a preso in valore assoluto si dice ampiezza della funzione sinusoidale.

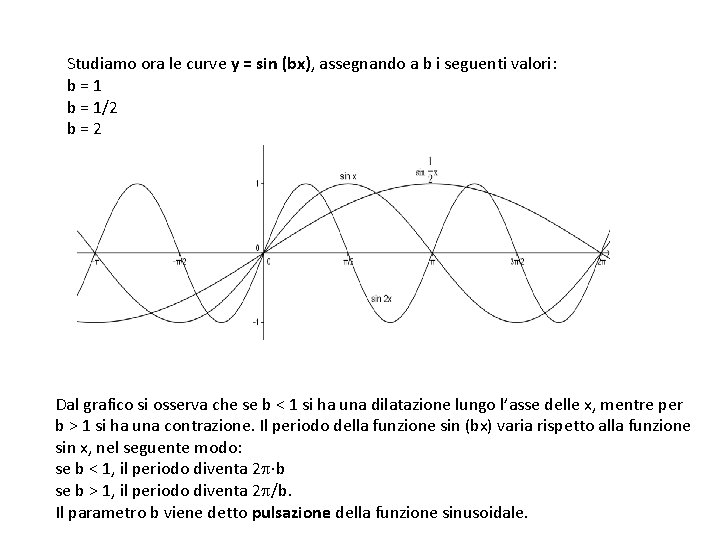
Studiamo ora le curve y = sin (bx), assegnando a b i seguenti valori: b = 1/2 b = 2 Dal grafico si osserva che se b < 1 si ha una dilatazione lungo l’asse delle x, mentre per b > 1 si ha una contrazione. Il periodo della funzione sin (bx) varia rispetto alla funzione sin x, nel seguente modo: se b < 1, il periodo diventa 2 b se b > 1, il periodo diventa 2 /b. Il parametro b viene detto pulsazione della funzione sinusoidale.

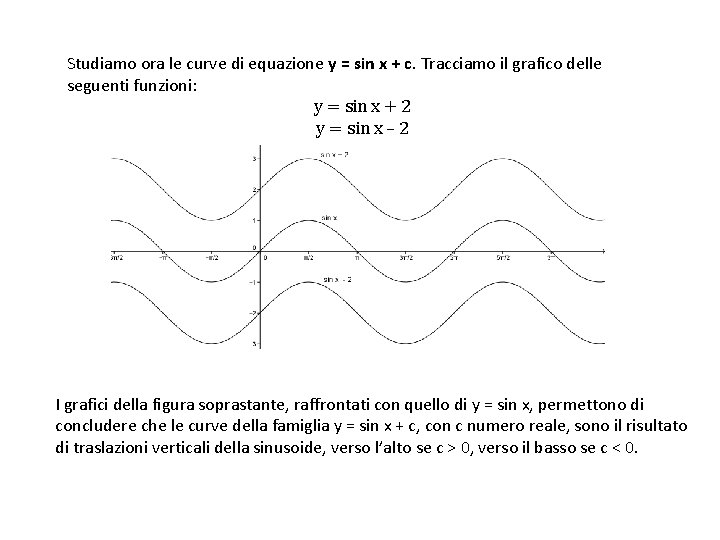
Studiamo ora le curve di equazione y = sin x + c. Tracciamo il grafico delle seguenti funzioni: y = sin x + 2 y = sin x – 2 I grafici della figura soprastante, raffrontati con quello di y = sin x, permettono di concludere che le curve della famiglia y = sin x + c, con c numero reale, sono il risultato di traslazioni verticali della sinusoide, verso l’alto se c > 0, verso il basso se c < 0.

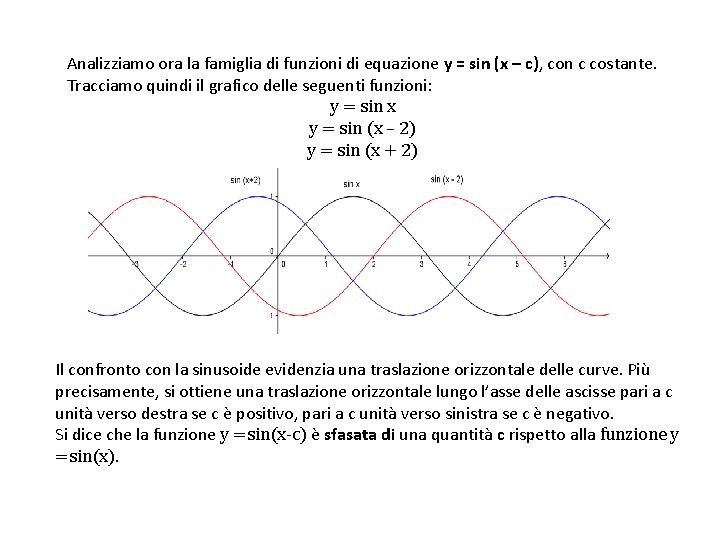
Analizziamo ora la famiglia di funzioni di equazione y = sin (x – c), con c costante. Tracciamo quindi il grafico delle seguenti funzioni: y = sin x y = sin (x – 2) y = sin (x + 2) Il confronto con la sinusoide evidenzia una traslazione orizzontale delle curve. Più precisamente, si ottiene una traslazione orizzontale lungo l’asse delle ascisse pari a c unità verso destra se c è positivo, pari a c unità verso sinistra se c è negativo. Si dice che la funzione y =sin(x-c) è sfasata di una quantità c rispetto alla funzione y =sin(x).

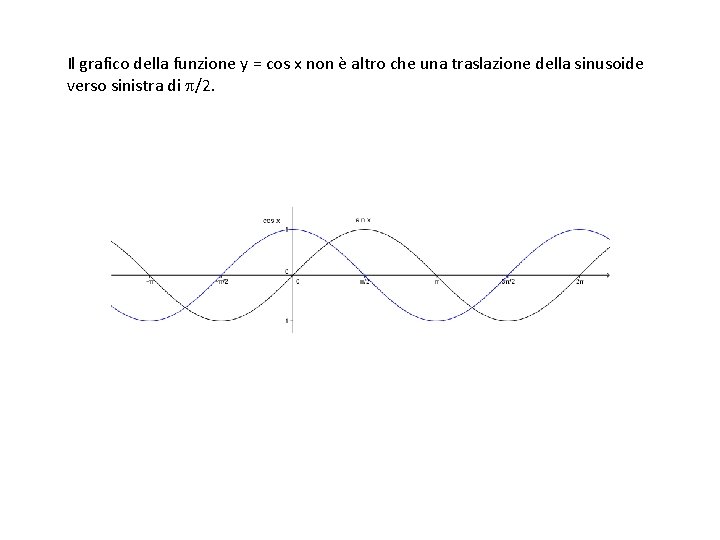
Il grafico della funzione y = cos x non è altro che una traslazione della sinusoide verso sinistra di /2.

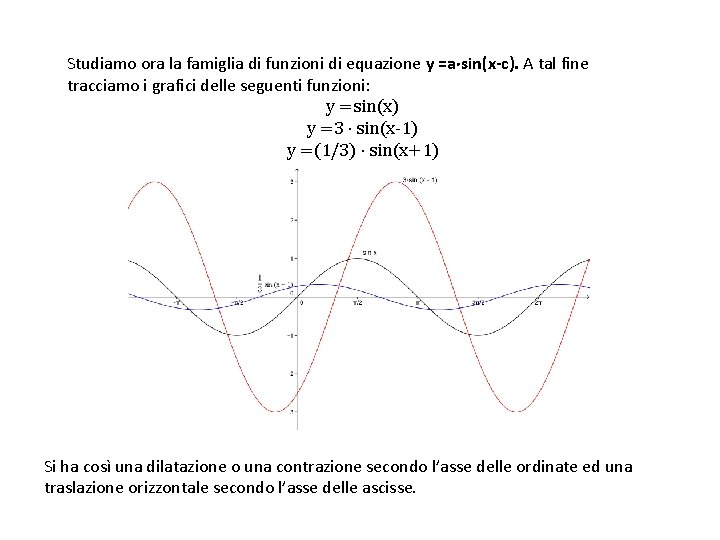
Studiamo ora la famiglia di funzioni di equazione y =a sin(x-c). A tal fine tracciamo i grafici delle seguenti funzioni: y =sin(x) y =3 sin(x-1) y =(1/3) sin(x+1) Si ha così una dilatazione o una contrazione secondo l’asse delle ordinate ed una traslazione orizzontale secondo l’asse delle ascisse.

Consideriamo ora il caso in cui una funzione sia data dalla somma algebrica di due o più funzioni. In tal caso il grafico relativo a tale funzione somma algebrica di due o più funzioni si ottiene sommando algebricamente i valori delle ordinate dei punti delle funzioni addendo in corrispondenza dello stesso valore di ascissa. Facciamo alcuni esempi.

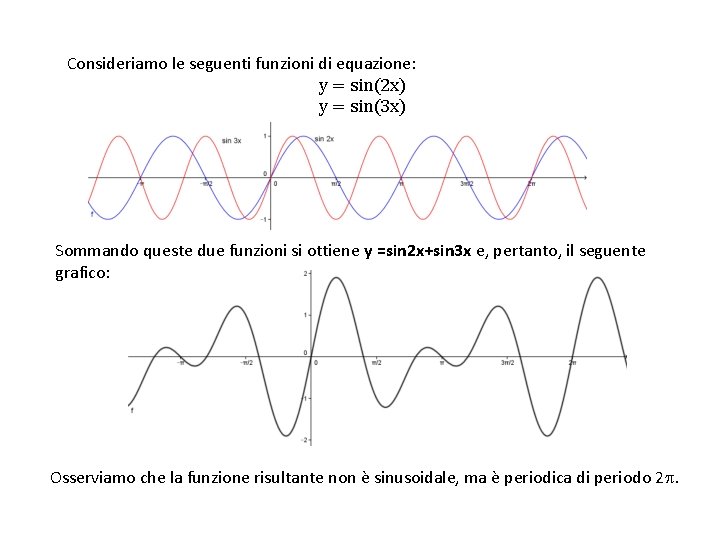
Consideriamo le seguenti funzioni di equazione: y = sin(2 x) y = sin(3 x) Sommando queste due funzioni si ottiene y =sin 2 x+sin 3 x e, pertanto, il seguente grafico: Osserviamo che la funzione risultante non è sinusoidale, ma è periodica di periodo 2.

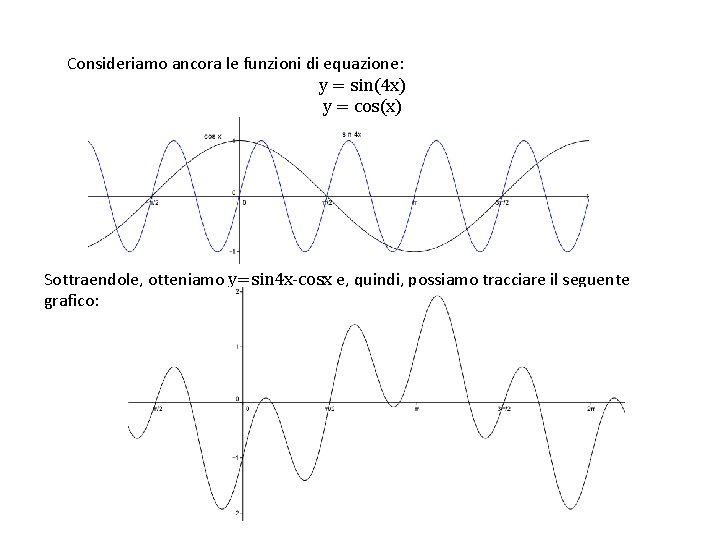
Consideriamo ancora le funzioni di equazione: y = sin(4 x) y = cos(x) Sottraendole, otteniamo y=sin 4 x-cosx e, quindi, possiamo tracciare il seguente grafico:

Quando si sommano due o più funzioni, dunque, la funzione risultante generalmente non è più una funzione sinusoidale come si può notare nei precedenti esempi. Tuttavia, la funzione risultante può ancora essere una funzione periodica. Si può dimostrare che la sovrapposizione di due funzioni sinusoidali di diverso periodo è una funzione periodica se solo se il rapporto fra i due periodi T 1 e T 2 è un numero razionale. Quindi, deve essere T 1/T 2 = m/n. Se la frazione m/n è ridotta ai minimi termini, il periodo della funzione risultante è T=n. T 1=m. T 2. La somma o sovrapposizione di due funzioni sinusoidali di uguale periodo, invece, è comunque ancora una funzione sinusoidale di uguale periodo a quello delle funzioni addendo.

In generale, una funzione y = f (x) è periodica di periodo T ( con T > 0 ) se si ha: (*) f ( x + k T ) = f (x) ovvero, se sostituendo ( x + k T ) al posto di x, il valore della funzione non cambia. Il più piccolo valore positivo di T viene detto minimo periodo principale. Le funzioni goniometriche, come sappiamo, sono periodiche e precisamente sen x e cos x hanno minimo periodo T = 360° oppure T = 2 , mentre tg x e ctg x hanno minimo periodo T = 180° oppure T = . Vediamo adesso, direttamente con alcuni esempi come si determina il periodo delle funzioni goniometriche.

Esercizi svolti 1. Determinare il periodo della funzione y = cos 2 x Sappiamo che la funzione coseno di un angolo è periodica quindi per la (*) si ha: cos [ 2(x + k T )] = cos 2 x → cos ( 2 x + 2 k T ) = cos 2 x essendo 360° il periodo del coseno di un angolo, si ha che il 2° membro dell’ultima eguaglianza si può scrivere come: cos 2 x = cos ( 2 x + k 360° ) quindi per transitività segue che 2. Determinare il periodo della funzione y = sin ( 3 x + a) Per la periodicità del seno di un angolo deve verificarsi la (*) e tenendo in considerazione il periodo di 2 del seno di un angolo si ha: sin [ 3 (x + k. T ) + a] = sin ( 3 x + a) = sin [( 3 x + a) + 2 k π] quindi segue che: sin [ 3 (x + k. T ) + a] = sin [( 3 x + a) + 2 k π ] → 3 (x + k. T ) + a = 3 x + a + 2 k π

Esercizi svolti 3. Determinare il periodo della funzione: Dobbiamo determinare T > 0 di modo che: Abbiamo un’equazione con la tangente ed essa è soddisfatta se e solo se:

Regola generale per la determinazione del periodo Dai due esercizi precedentemente svolti possiamo dedurre la regola generale per la determinazione del periodo di funzioni goniometriche. Infatti se dobbiamo determinare il periodo della funzione di equazione generale: y = a sin (ω x + ) procediamo al solito nel seguente modo: a sin [ ω (x + k T ) + β ] = a sin [(ω x + β ) +2 k π ] da cui ω (x + k T ) + = ω x + +2 k π Quindi il periodo generale del seno e del coseno di un angolo è Analogamente si procede per la determinazione del periodo minimo della tangente o della cotangente di un angolo, basta solo sostituire il loro periodo π nella regola precedente al posto di 2 , cioè:

Esercizi Determinare il periodo delle seguenti funzioni: 1) 2) 3) 4) 5) y = sin (5 x) y = 2 ⋅ cos(4 x) y = 3 ⋅ tg(4 x+ /2) y = sin(3 x) + cos(2 x) y = 2 ⋅ sin(4 x) + cos (5 x) + 3 ⋅ tg (3 x - )