Il metodo topografico 1 2 3 4 5

Il metodo topografico 1. 2. 3. 4. 5. 6. 7. 8. La topografia classica Il punto referente e i punti cartografici Misura degli angoli di direzione Angoli e distanze: la stazione totale Metodi mensori Morfologia delle reti Simulazione dell’incertezza livellazioni

OGGETTO TOPOGRAFICO TOPOGRAFIA è la tecnica di costruzione di un modello geometrico di una porzione di superficie terrestre compresa entro una regione topografica (introno di 15 km) ovvero un campo nel quale si può considerare trascurabile l'errore di sfericità del geoide terrestre.

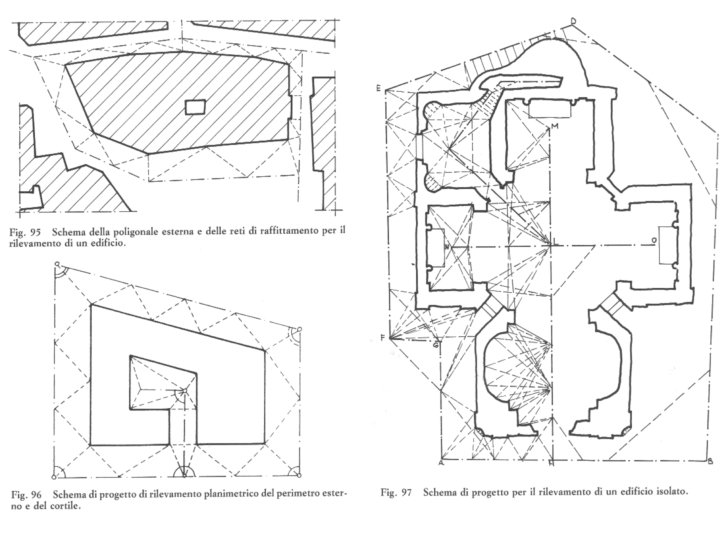
RILEVAMENTO TOPOGRAFICO Individuazione delle posizioni relative di un certo numero di punti della regione topografica disposti secondo un’ossatura fondamentale – detta rete d'appoggio – e, successivamente individuati in luoghi via più particolari, e loro rappresentazione in un modello geometrico, generalmente in proiezione planimetrica, e altimetrica.

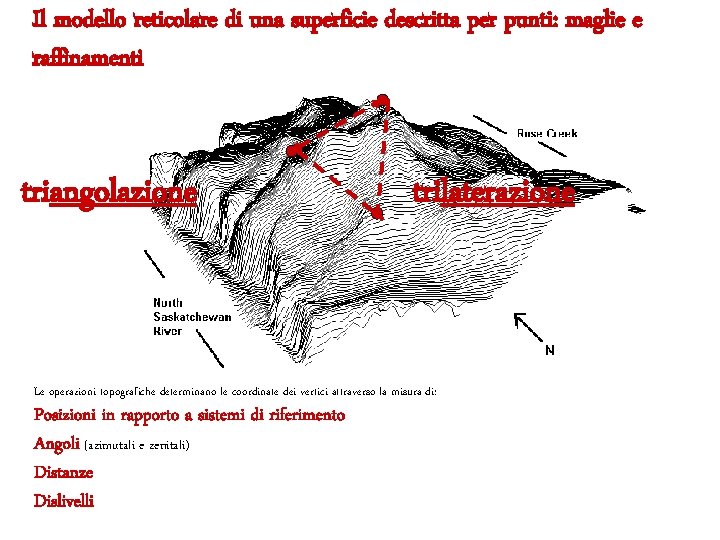
Il modello reticolare di una superficie descritta per punti: maglie e raffinamenti triangolazione trilaterazione Le operazioni topografiche determinano le coordinate dei vertici attraverso la misura di: Posizioni in rapporto a sistemi di riferimento Angoli (azimutali e zenitali) Distanze Dislivelli

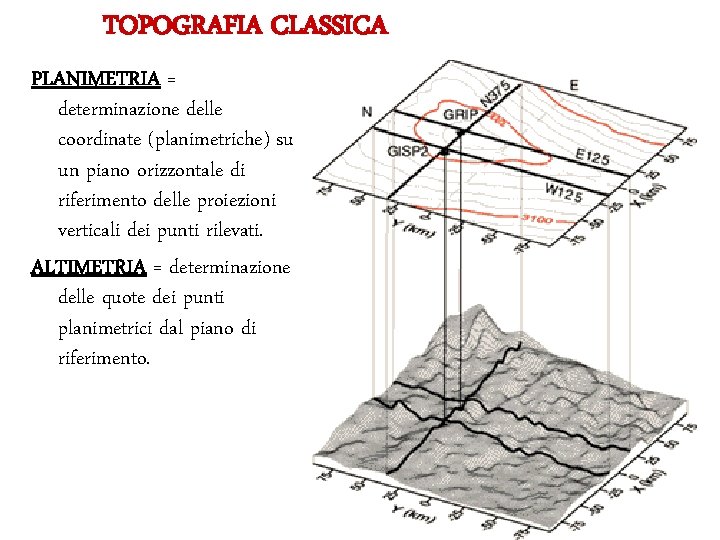
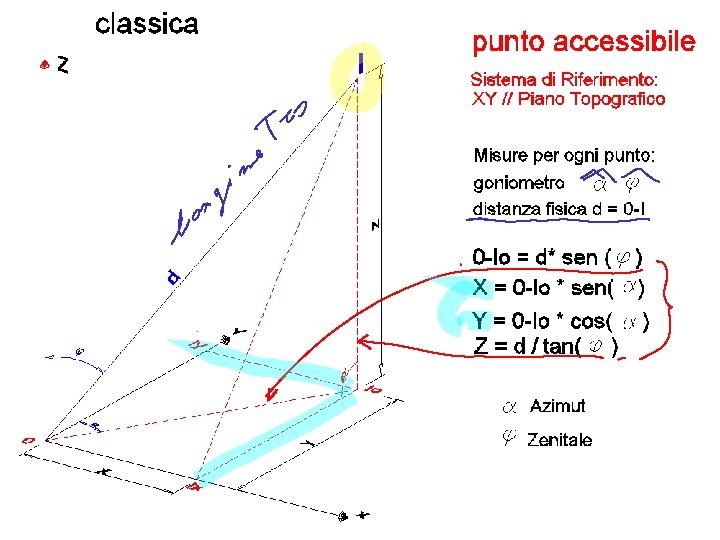
TOPOGRAFIA CLASSICA PLANIMETRIA = determinazione delle coordinate (planimetriche) su un piano orizzontale di riferimento delle proiezioni verticali dei punti rilevati. ALTIMETRIA = determinazione delle quote dei punti planimetrici dal piano di riferimento.

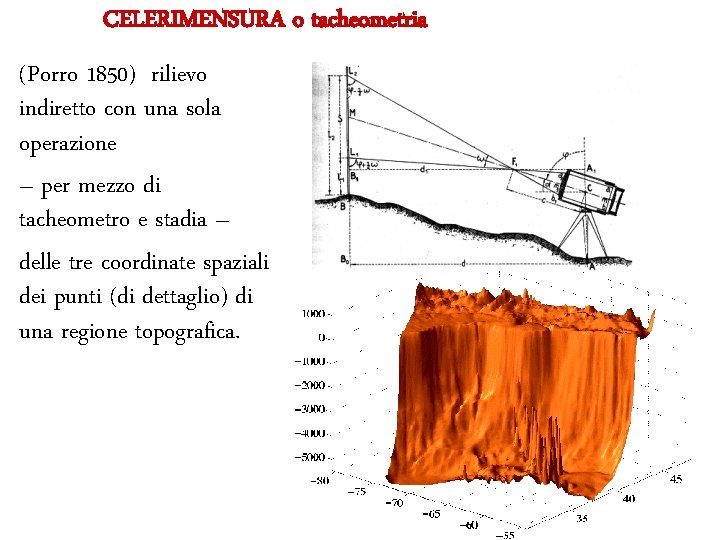
CELERIMENSURA o tacheometria (Porro 1850) rilievo indiretto con una sola operazione – per mezzo di tacheometro e stadia – delle tre coordinate spaziali dei punti (di dettaglio) di una regione topografica.

Il metodo topografico 1. 2. 3. 4. 5. 6. 7. 8. La topografia classica Il punto referente e i punti cartografici Misura degli angoli di direzione Angoli e distanze: la stazione totale Metodi mensori Morfologia delle reti Simulazione dell’incertezza livellazioni

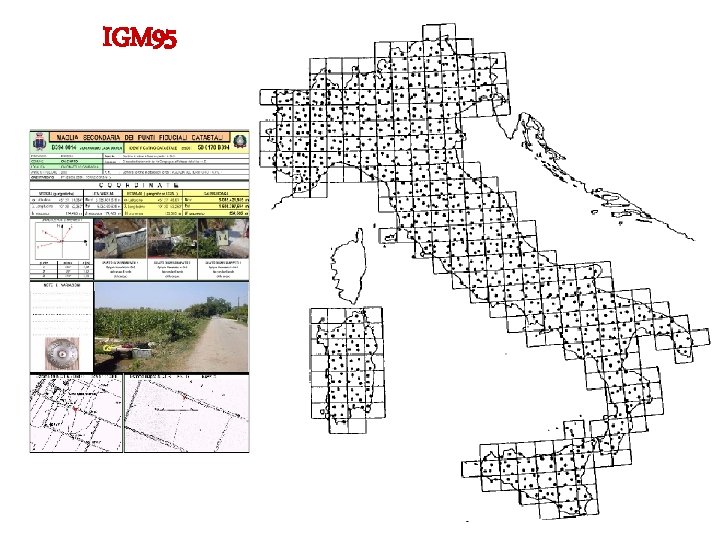
Dove si trova un punto? - ITRS (International Terrestrial Riferiment System) - Successive realizzazioni … ITRF (…Frame), ETRF (Europe …), - IGM 95 Rete geodetica fondamentale italiana dell’Istituto Geografico Militare - 1200 caposaldi monografati in ETRF 89

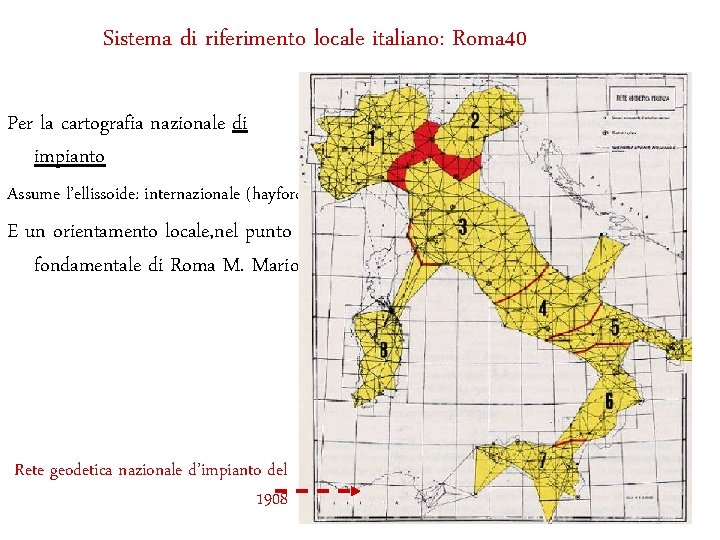
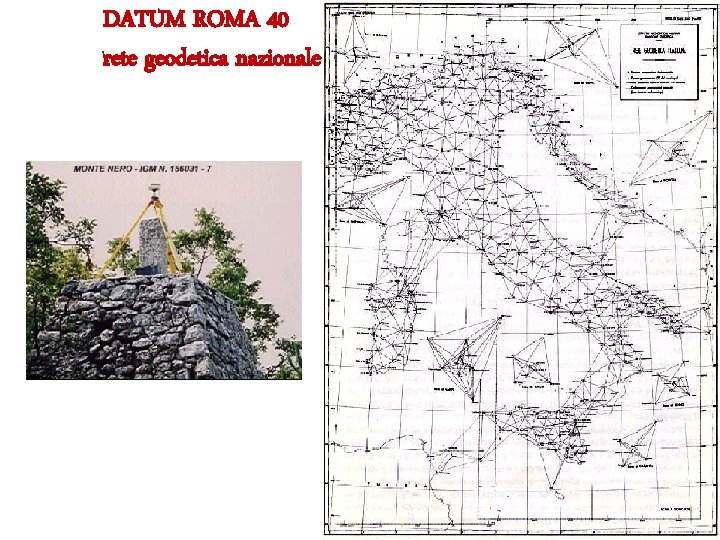
Sistema di riferimento locale italiano: Roma 40 Per la cartografia nazionale di impianto Assume l’ellissoide: internazionale (hayford) E un orientamento locale, nel punto fondamentale di Roma M. Mario Rete geodetica nazionale d’impianto del 1908

DATUM ROMA 40 rete geodetica nazionale

IGM 95

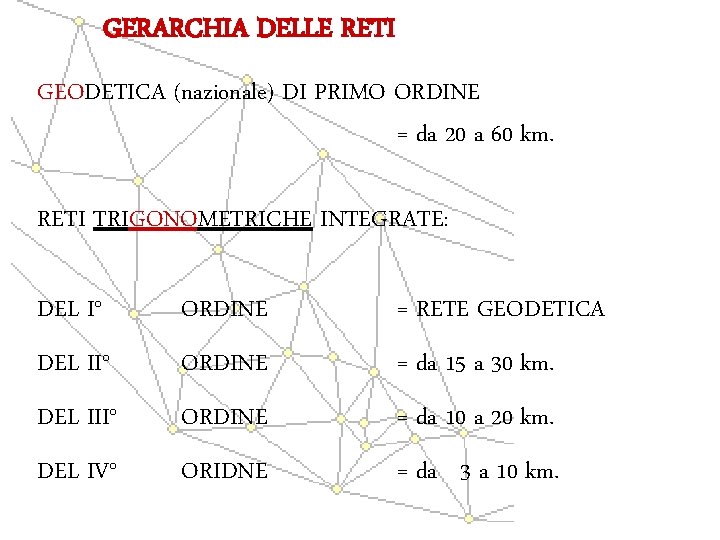
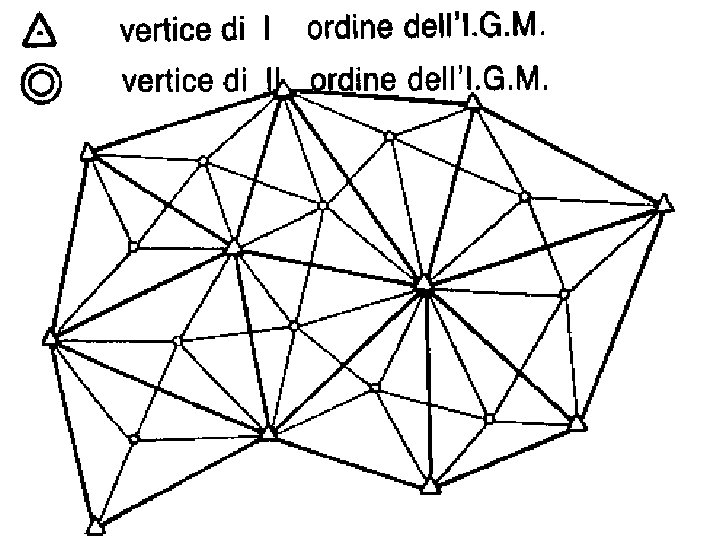
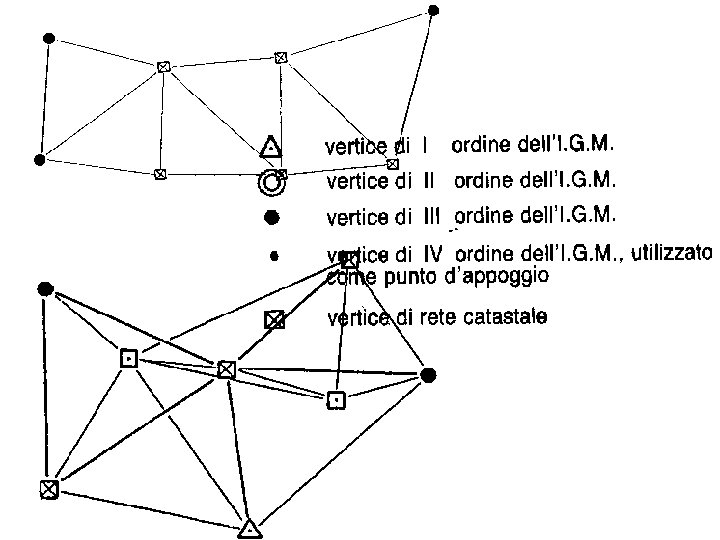
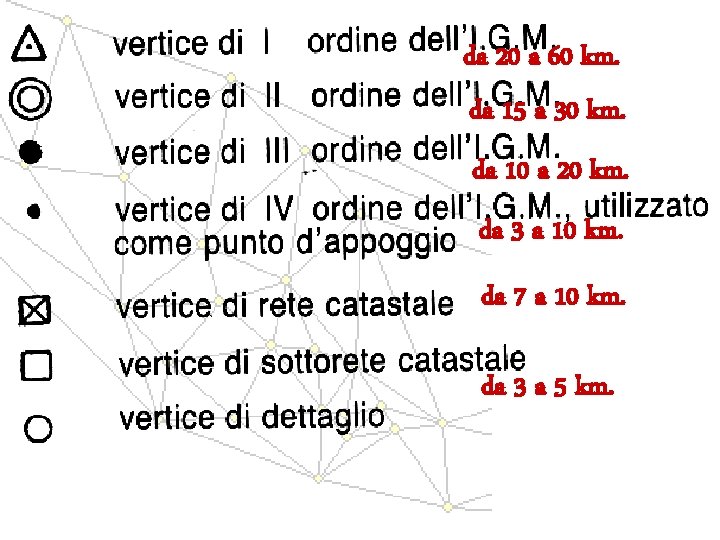
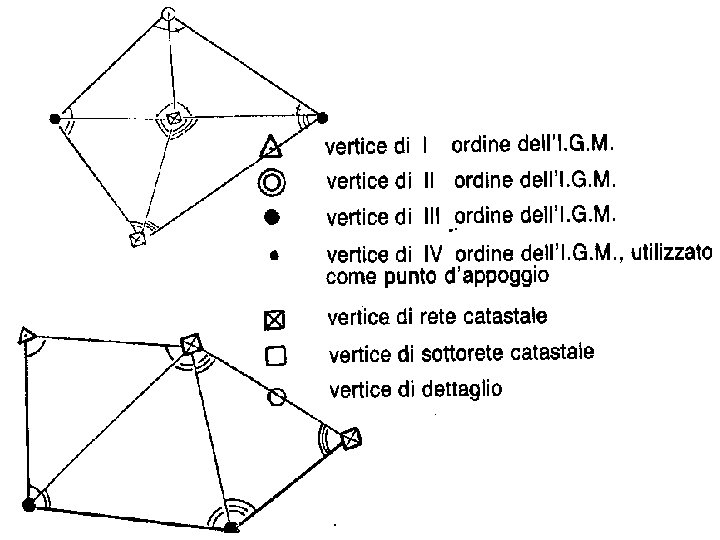
GERARCHIA DELLE RETI GEODETICA (nazionale) DI PRIMO ORDINE = da 20 a 60 km. RETI TRIGONOMETRICHE INTEGRATE: DEL I° ORDINE = RETE GEODETICA DEL II° ORDINE = da 15 a 30 km. DEL III° ORDINE = da 10 a 20 km. DEL IV° ORIDNE = da 3 a 10 km.

da 20 a 60 km. da 15 a 30 km. da 10 a 20 km. da 3 a 10 km. da 7 a 10 km. da 3 a 5 km.

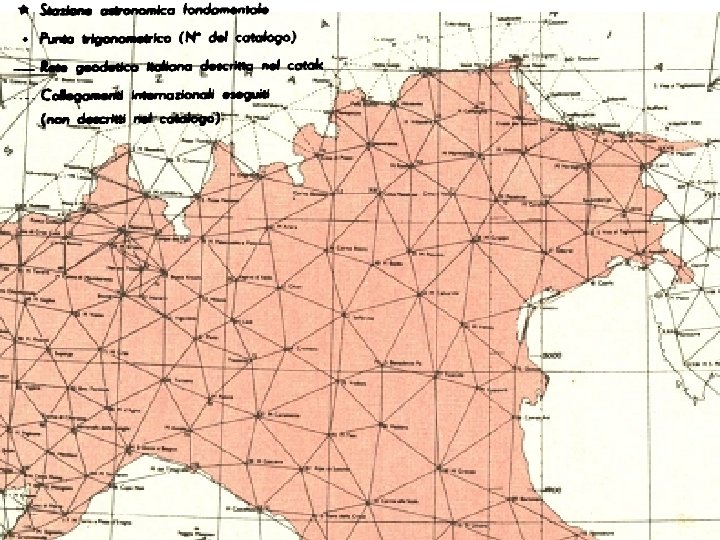
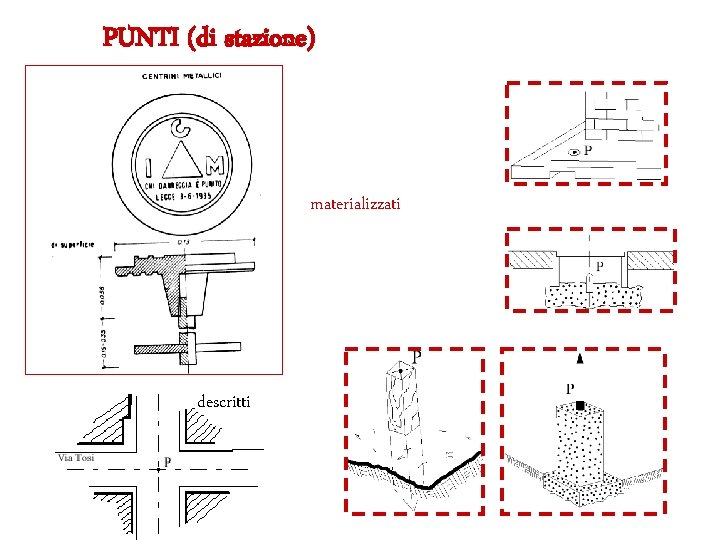
PUNTI (di stazione) materializzati descritti

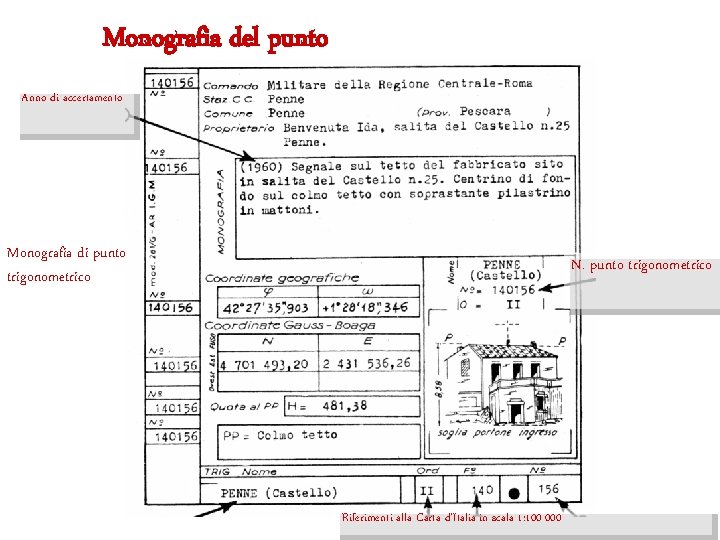
Monografia del punto Anno di accertamento Monografia di punto trigonometrico N. punto trigonometrico Riferimenti alla Carta d’Italia in scala 1: 100 000

PUNTI (collimati)

Il metodo topografico 1. 2. 3. 4. 5. 6. 7. 8. La topografia classica Il punto referente e i punti cartografici Misura degli angoli di direzione Angoli e distanze: la stazione totale Metodi mensori Morfologia delle reti Simulazione dell’incertezza livellazioni

OPERAZONI DI RILEVAMENTO TRACCIAMENTO DEI PIANI DEGLI ALLINEAMENTI E DEI PUNTI Tipo di strumenti Livelli Segnali di punti e di piani Traguardi, scopi MISURA DIRETTA DEGLI ANGOLI Goniometri azimutali MISURA DIRETTA DELLE DISTANZE Longimetri diretti MISURA INDIRETTA DELLE DISTANZE MISURA DEI LIVELLI azimutali e zenitali Goniografi Distanziometri Telemetri Stadimetri Clisimetri

Angoli: letture fino ai cc Grado centesimale la 400 ma parte dell’angolo giro primo centesimale, la 100 ma parte del grado secondo centesimale, la 100 ma parte del primo 60 g , 40 c , 37 cc = 60, 4037

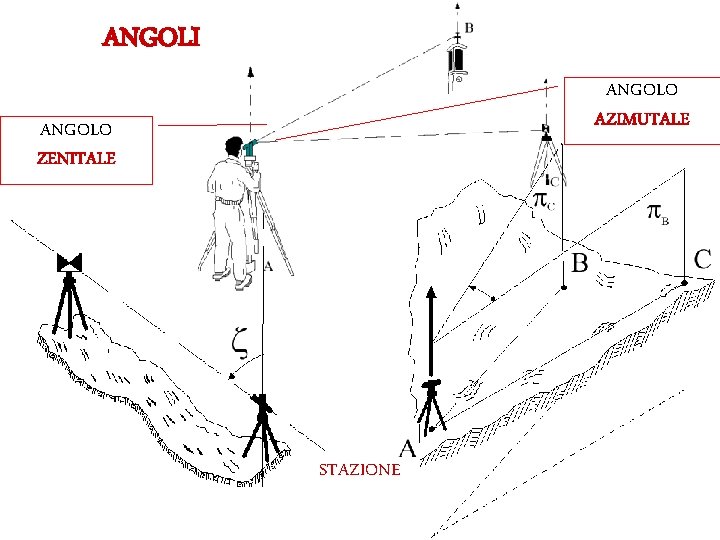
ANGOLI ANGOLO AZIMUTALE ANGOLO ZENITALE STAZIONE

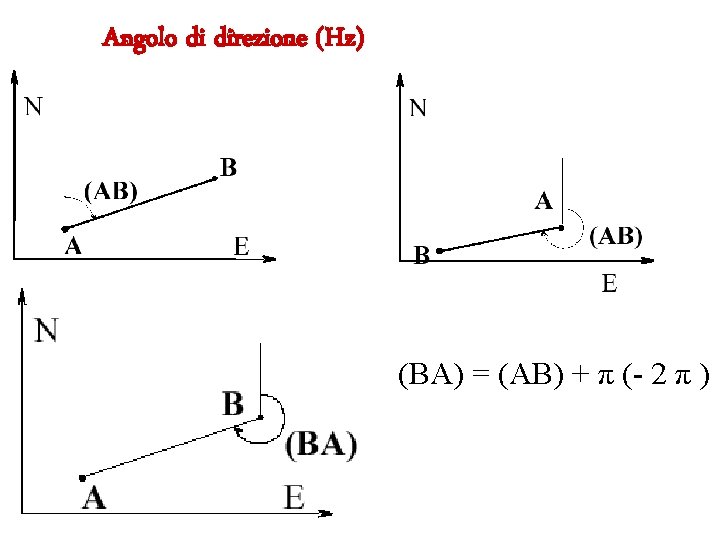
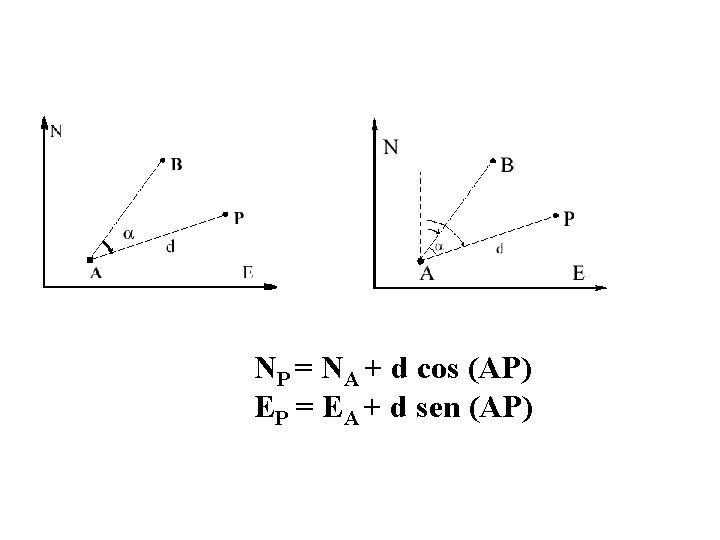
Angolo di direzione (Hz) (BA) = (AB) + π (- 2 π )

NP = NA + d cos (AP) EP = EA + d sen (AP)

GONIOMETRI A traguardo azimutali Squadro graduato Bussola a traguardi A prisma rifrengente (squadro graduato a prima) Azimutale a cannocchiale A cannocchiale - Bussola a cannocchiale Squadro graduato a cannocchiale A traguardo azimutali e zenitali A cannocchiale Goniografi Tavoletta pretoriana Tacheometro Teodolite

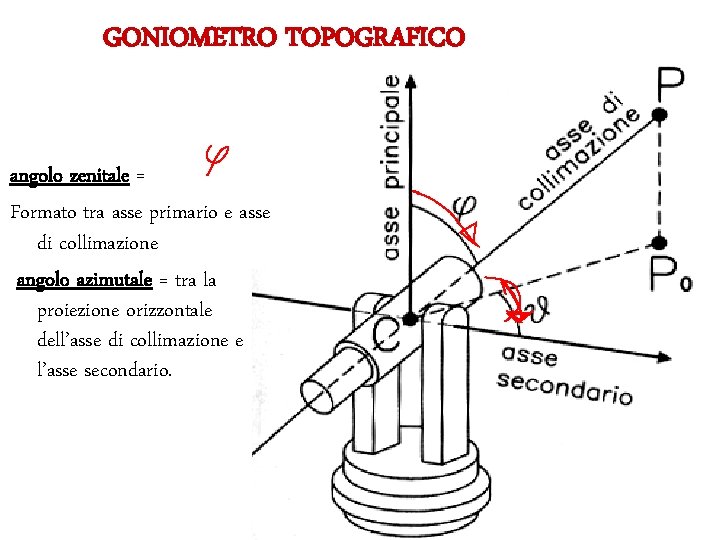
GONIOMETRO TOPOGRAFICO angolo zenitale = Formato tra asse primario e asse di collimazione angolo azimutale = tra la proiezione orizzontale dell’asse di collimazione e l’asse secondario.

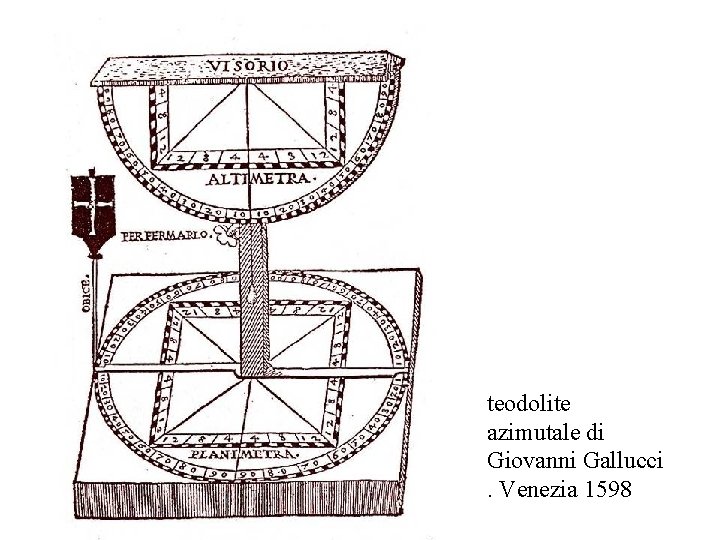
teodolite azimutale di Giovanni Gallucci . Venezia 1598

cannocchiale alidada piatto basamento

MESSA IN STAZIONE: 1 il tripode

2 la basetta Agendo su dispositivi di regolazione del basetta e degli strumenti che vi verranno innestati 1) si materializza la verticale che collim il punto di stazione segnato a terra 2) Si assicura l’orizzontalità dell’appog

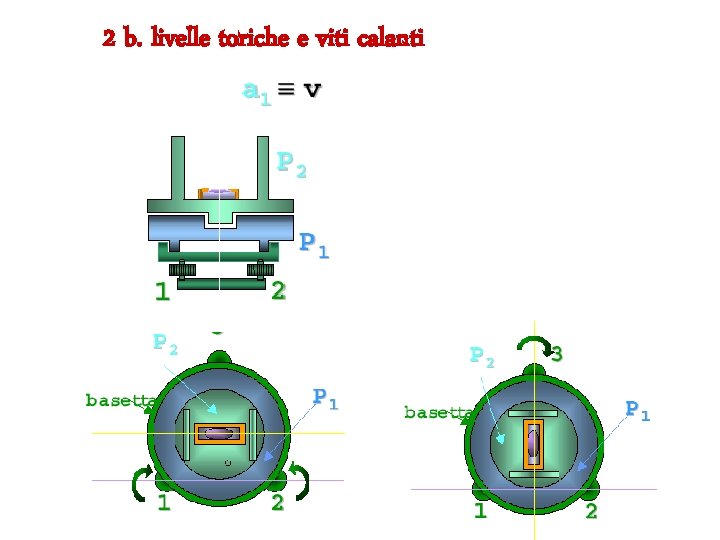
2 b. livelle toriche e viti calanti

Il metodo topografico 1. 2. 3. 4. 5. 6. 7. 8. La topografia classica Il punto referente e i punti cartografici Misura degli angoli di direzione Angoli e distanze: la stazione totale Metodi mensori Morfologia delle reti Simulazione dell’incertezza livellazioni

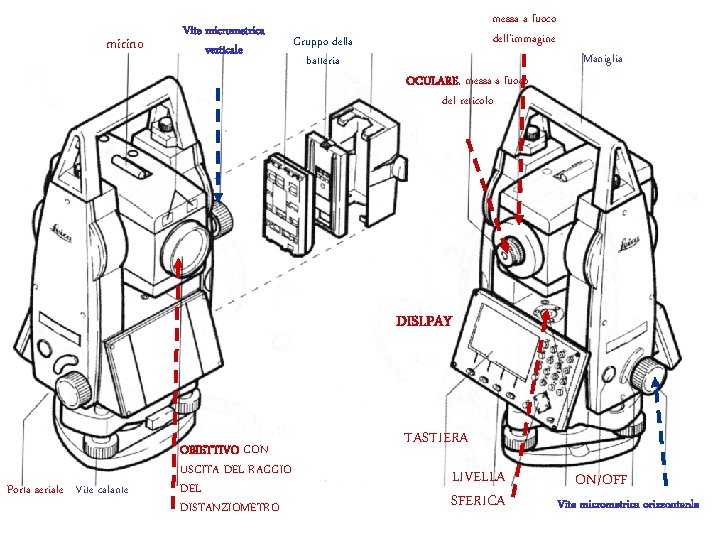
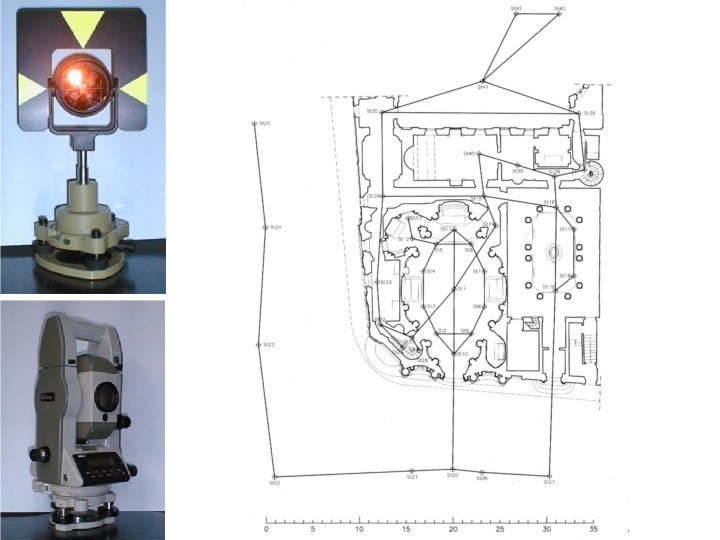
mirino Vite micrometrica verticale Gruppo della batteria messa a fuoco dell’immagine Maniglia OCULARE, messa a fuoco del reticolo DISLPAY Porta seriale Vite calante OBIETTIVO CON USCITA DEL RAGGIO DEL DISTANZIOMETRO TASTIERA LIVELLA SFERICA ON/OFF Vite micrometrica orizzontanle

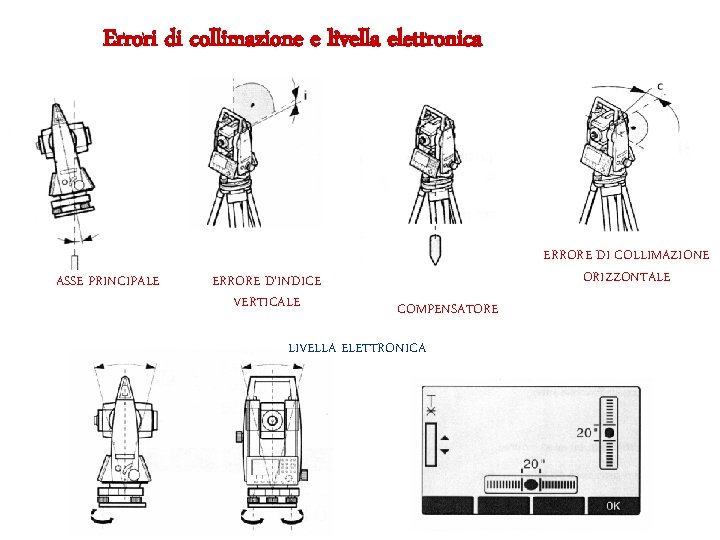
Errori di collimazione e livella elettronica ASSE PRINCIPALE ERRORE D’INDICE VERTICALE ERRORE DI COLLIMAZIONE ORIZZONTALE COMPENSATORE LIVELLA ELETTRONICA

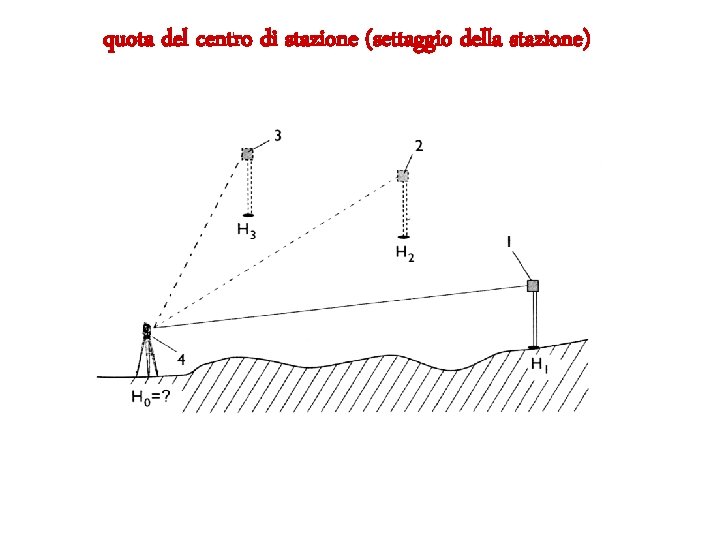
quota del centro di stazione (settaggio della stazione)

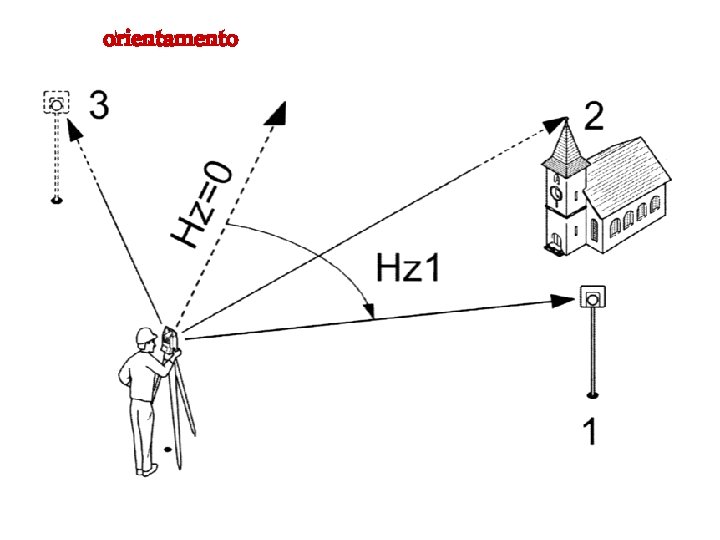
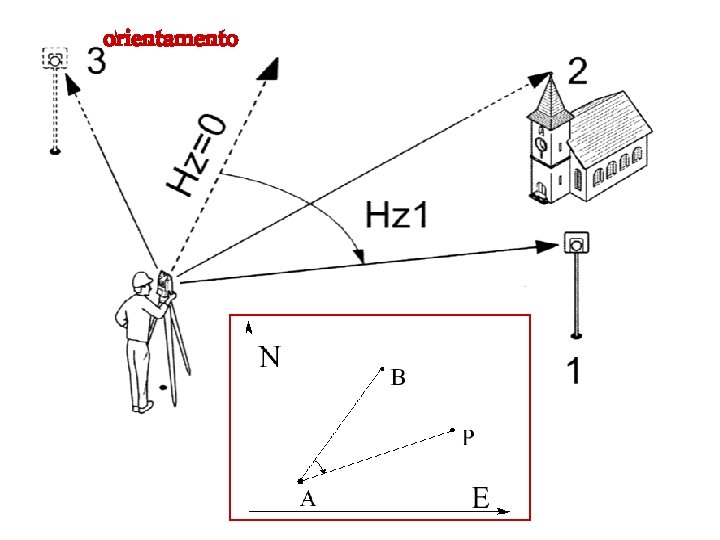
orientamento

orientamento

Note le coordinate di un primo punto E l’azimut di un primo lato Misura delle basi (distanze tra punti di stazione)

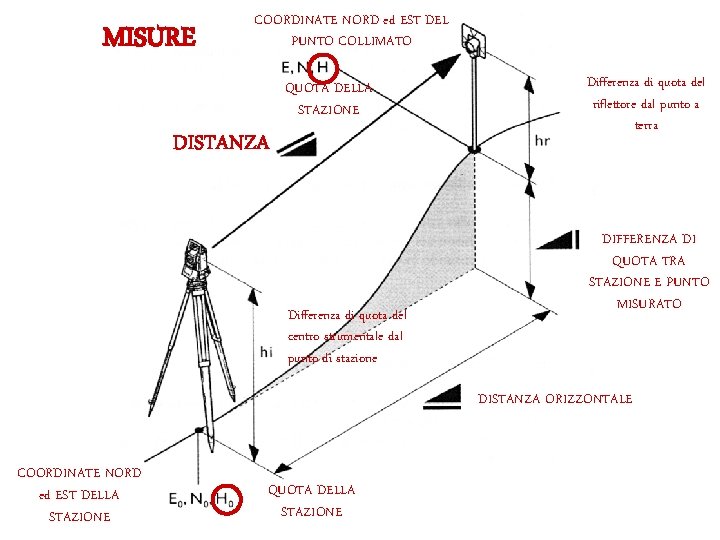
MISURE COORDINATE NORD ed EST DEL PUNTO COLLIMATO QUOTA DELLA STAZIONE DISTANZA Differenza di quota del centro strumentale dal punto di stazione Differenza di quota del riflettore dal punto a terra DIFFERENZA DI QUOTA TRA STAZIONE E PUNTO MISURATO DISTANZA ORIZZONTALE COORDINATE NORD ed EST DELLA STAZIONE QUOTA DELLA STAZIONE

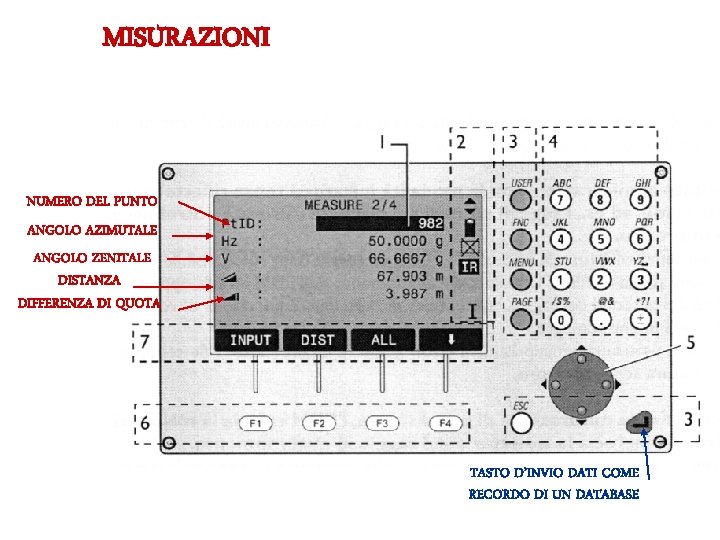
MISURAZIONI NUMERO DEL PUNTO ANGOLO AZIMUTALE ANGOLO ZENITALE DISTANZA DIFFERENZA DI QUOTA TASTO D’INVIO DATI COME RECORDO DI UN DATABASE

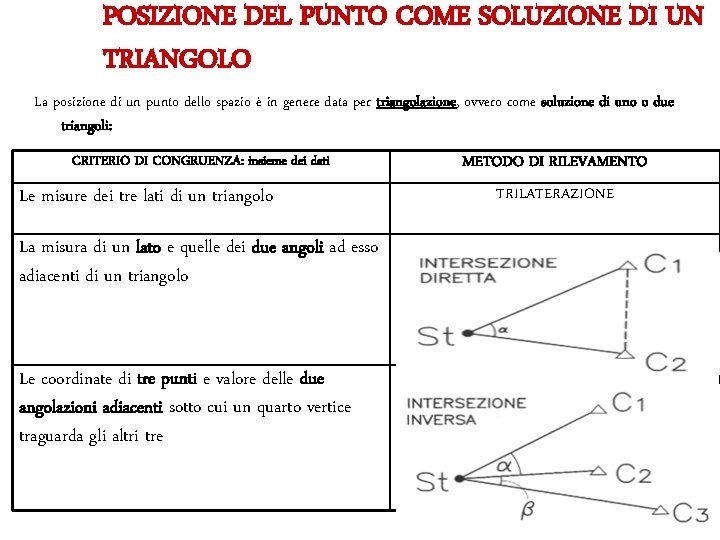
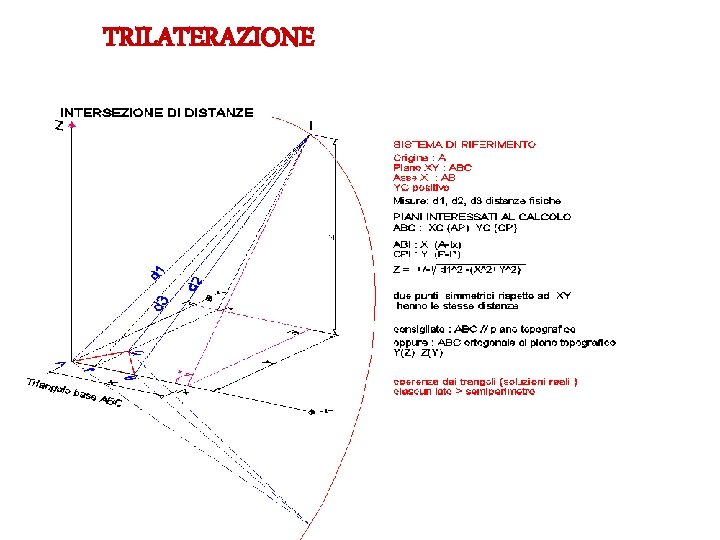
POSIZIONE DEL PUNTO COME SOLUZIONE DI UN TRIANGOLO La posizione di un punto dello spazio è in genere data per triangolazione, ovvero come soluzione di uno o due triangoli: CRITERIO DI CONGRUENZA: insieme dei dati Le misure dei tre lati di un triangolo La misura di un lato e quelle dei due angoli ad esso adiacenti di un triangolo Le coordinate di tre punti e valore delle due angolazioni adiacenti sotto cui un quarto vertice traguarda gli altri tre METODO DI RILEVAMENTO TRILATERAZIONE

TRILATERAZIONE

Il metodo topografico 1. 2. 3. 4. 5. 6. 7. 8. La topografia classica Il punto referente e i punti cartografici Misura degli angoli di direzione Angoli e distanze: la stazione totale Metodi mensori Morfologia delle reti Simulazione dell’incertezza livellazioni

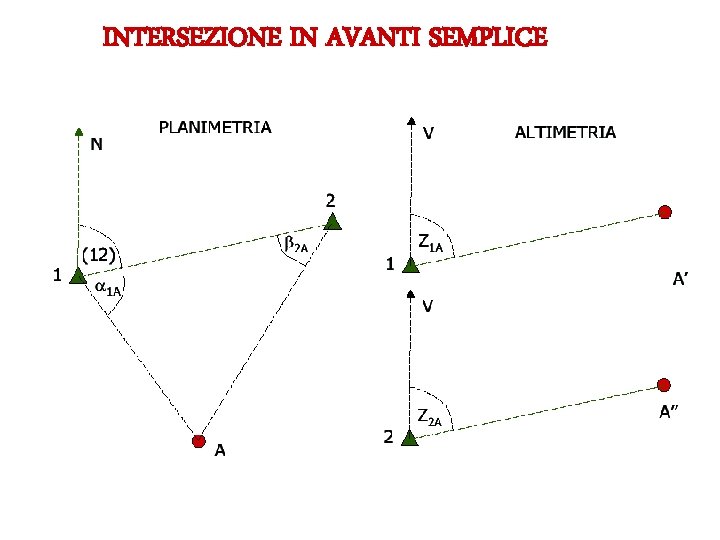
INTERSEZIONE IN AVANTI SEMPLICE

INTERSEZIONE IN AVANTI SEMPLICE 1) 2) 3) Calcolo della distanza tra i due punti di stazione 1 -2 Calcolo dell’angolo di direzione 1 -2 Misurati 1 A e 2 A si calcolano le coordinate di A 4) Dati strettamente necessari ma non sufficienti al controllo delle operazione di misura (gli errori di misura dei due angoli non sarebbero evidenziabili)

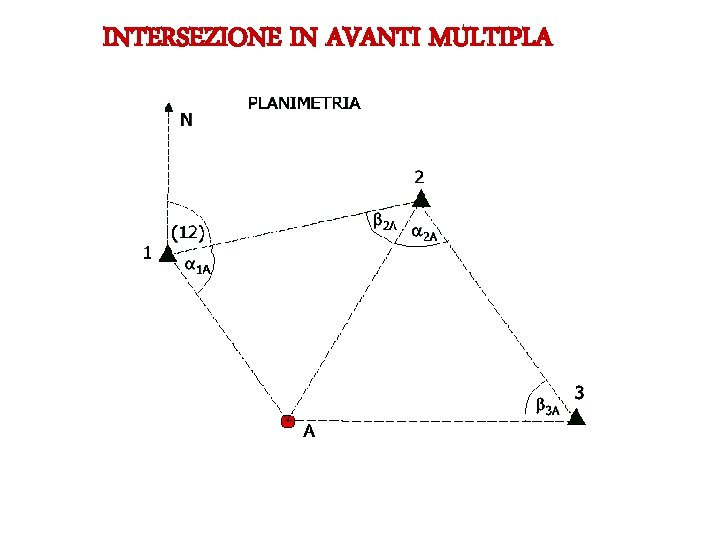
INTERSEZIONE IN AVANTI MULTIPLA

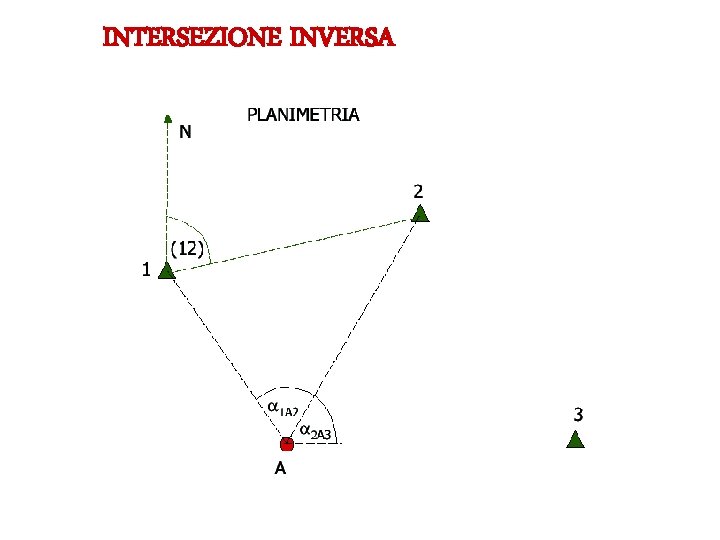
INTERSEZIONE INVERSA

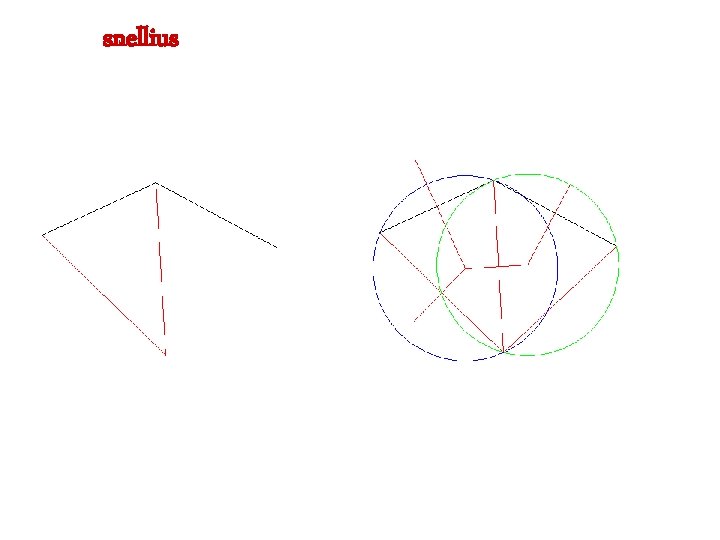
snellius

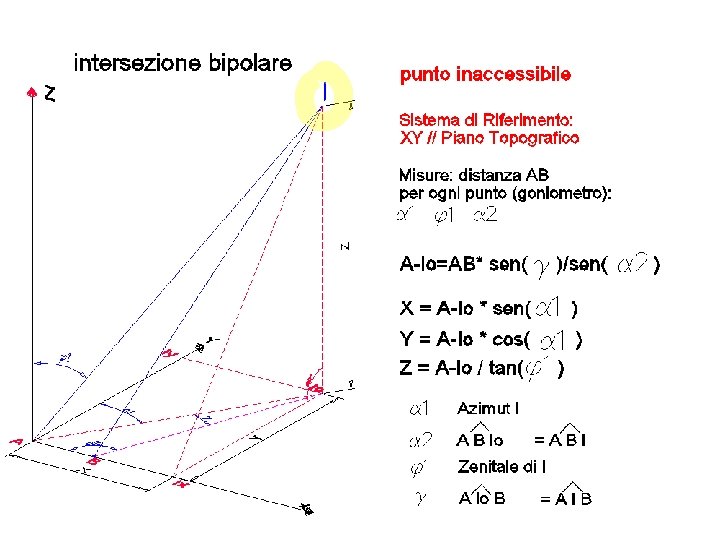
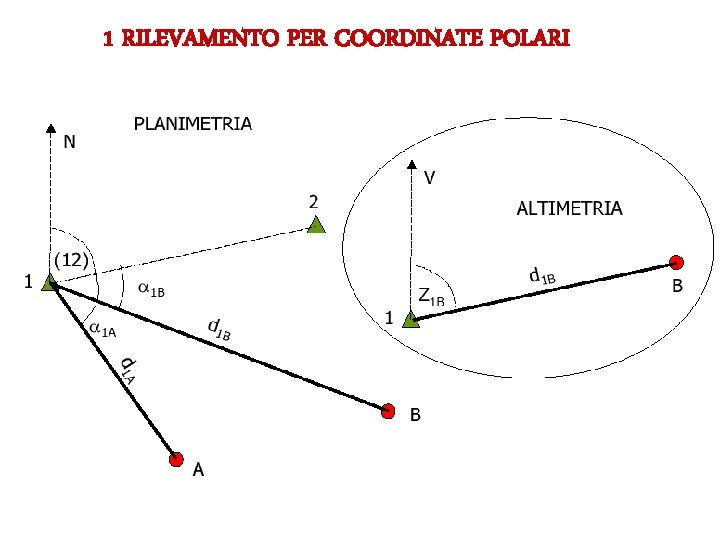
PRINCIPALI SISTEMI DI RILEVAMENTO metodo PER CCORDINATE POLARI (IRRAGGIAMENTO) PER COORDINATE BIPOLARI (INTERSEZIONE IN AVANTI) determinazione delle coordinate di un punto tramite: i due angoli dell’asse di collimazione e distanza del punto dal centro strumentale i due angoli dell’asse di collimazione dello stesso punto da ciascuna di una coppia di stazioni a distanza reciproca nota

1 RILEVAMENTO PER COORDINATE POLARI

Il metodo topografico 1. 2. 3. 4. 5. 6. 7. 8. La topografia classica Il punto referente e i punti cartografici Misura degli angoli di direzione Angoli e distanze: la stazione totale Metodi mensori Morfologia delle reti Simulazione dell’incertezza livellazioni

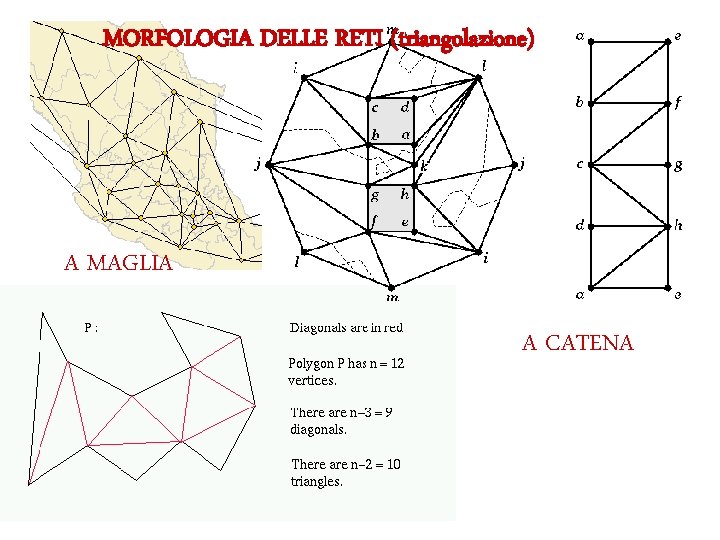
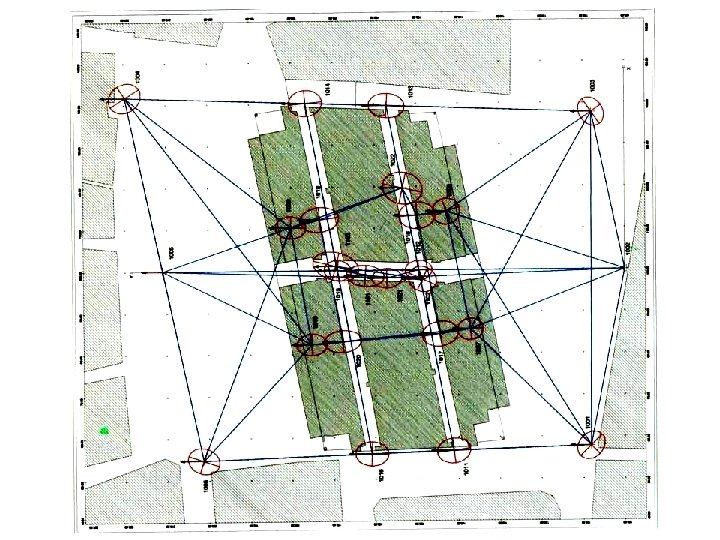
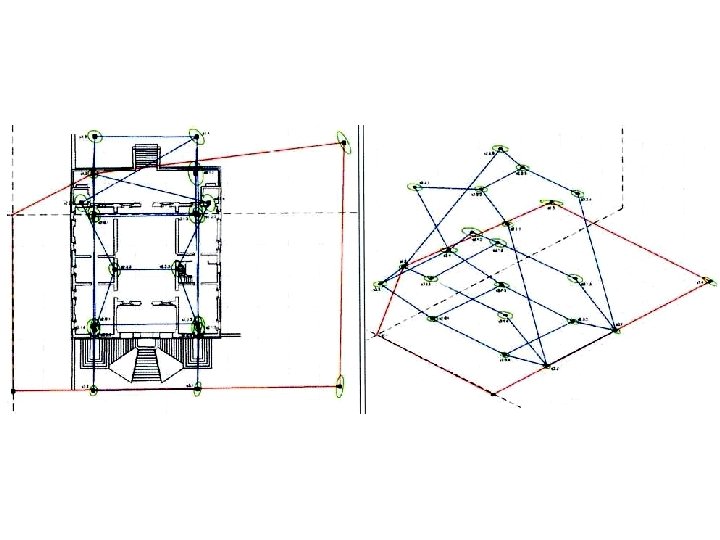
MORFOLOGIA DELLE RETI (triangolazione) A MAGLIA A CATENA

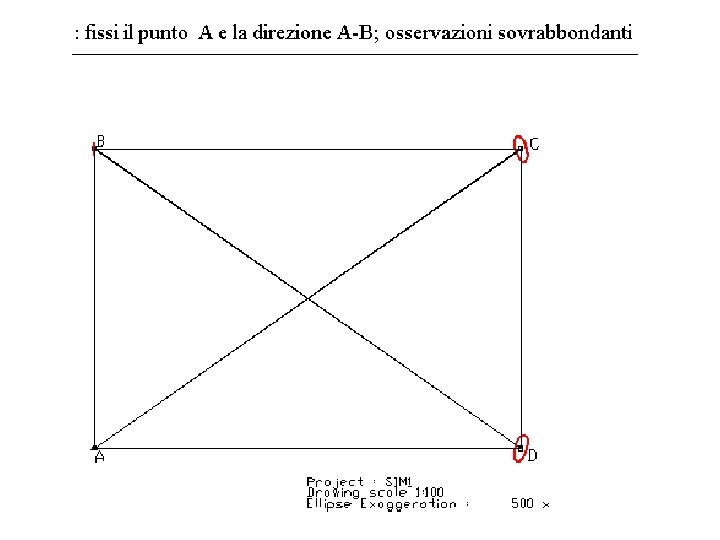
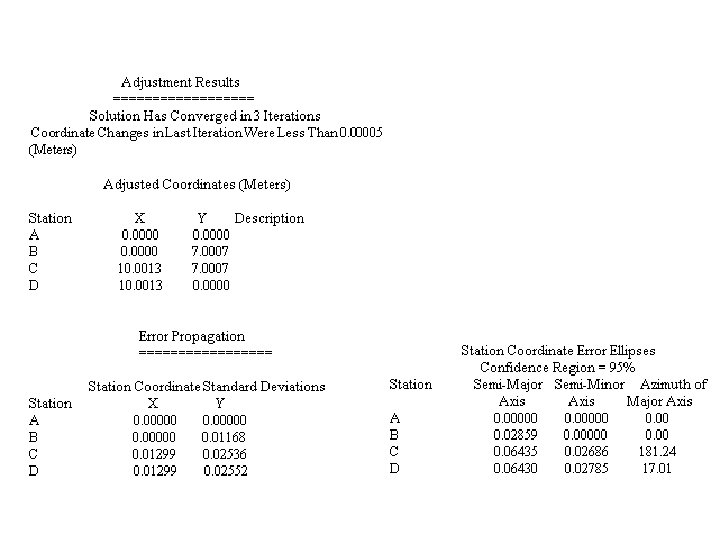
TRALATERI E MISURE SOVRABBONDANDANTI

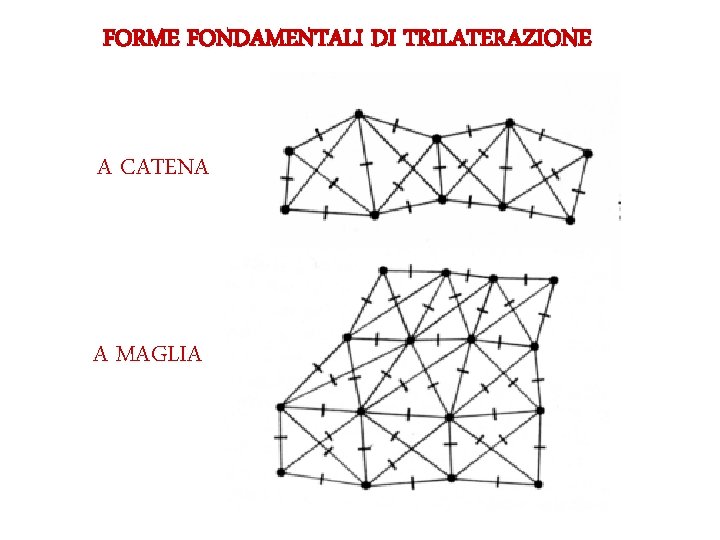
FORME FONDAMENTALI DI TRILATERAZIONE A CATENA A MAGLIA

Il metodo topografico 1. 2. 3. 4. 5. 6. 7. 8. La topografia classica Il punto referente e i punti cartografici Misura degli angoli di direzione Angoli e distanze: la stazione totale Metodi mensori Morfologia delle reti Simulazione dell’incertezza livellazioni

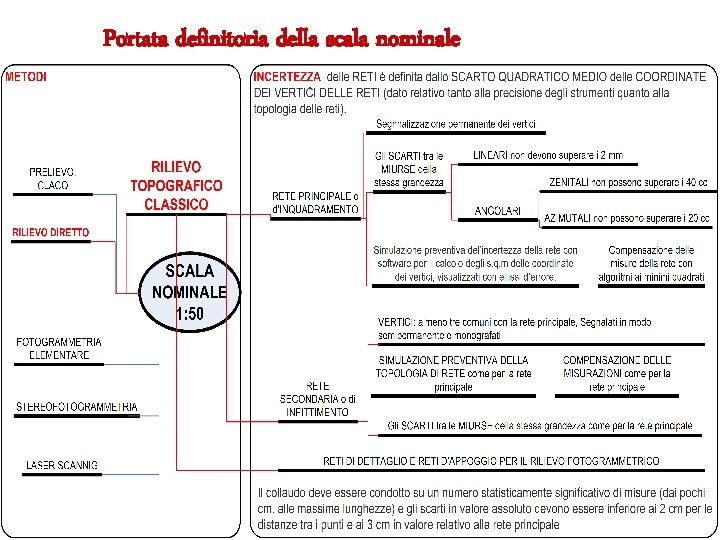
Portata definitoria della scala nominale

misure angolari azimutali a) 1) Angoli azimutali: devono essere misurati almeno una volta nelle due posizioni coniugate dello strumento. Le osservazioni angolari devono essere ripetute qualora la differenza fra le due letture coniugate risulti essere diversa dall'angolo piatto di una quantità superiore a: 60 cc nel caso in cui il goniometro impiegato per le osservazioni azimutali consenta la lettura diretta di 20 cc; 2 c nel caso in cui il goniometro impiegato per le osservazioni azimutali consenta la lettura diretta di 1 c. Le osservazioni degli angoli azimutali si fanno possibilmente al piede delle paline poste verticalmente sui vertici della poligonale. Il vertice collimato deve essere segnalato con opportuni accorgimenti ( filo a piombo, centramento forzato, ecc. ) che evitino nella collimazione apprezzamenti a stima da parte dell'operatore, quando il vertice dello stesso è collocato a distanza inferiore a: 200 m per le poligonali rilevate con goniometro che consente la lettura diretta di 20 cc; 50 m per le poligonali rilevate con goniometro che consente la letture diretta di 1 c.

misure angolari zenitali devono essere misurati almeno una volta nelle due posizioni coniugate dello strumento. Le osservazioni angolari devono essere ripetute qualora la somma delle due letture coniugate risulta essere diversa dall'angolo giro di una quantità superiore a: 60 cc nel caso in cui il goniometro impiegato per le osservazioni zenitali consenta una lettura diretta di 20 cc; 2 c nel caso in cui il goniometro impiegato per le osservazioni zenitali consenta la lettura diretta di 1 c. Per quanto possibile le visuali dovranno avere angoli zenitali compresi tra 80 e 120 gradi centesimali.

Misura delle distanze con longimetro t=0. 008 sqrt(D)+0. 0002 D in terreno piano t=0. 010 sqrt(D)+0. 0002 D in terreno ondulato t=0. 015 sqrt(D)+0. 0002 D in terreno sfavorevole.

Misura della distanza con distanziometro elettro -ottico la misura della distanza inclinata relativa a ciascun lato della poligonale deve essere ripetuta almeno due volte in ciascun vertice; se tra le due misure effettuate dallo stesso vertice la differenza, considerata in valore assoluto, è superiore a 3 cm si dovrà eseguire una terza misura e scartare tra le osservazioni effettuate quella che risulta errata; la differenza tra le misure di uno stesso lato della poligonale effettuate da due estremi e ridotte all'orizzonte, considerata al valore assoluto, deve essere inferiore a 4 cm. Come valore delle grandezze osservate, sia lineari che angolari, si assumono i valori opportunamente mediati delle misure, qualora queste ultime rientrino nei limiti di tolleranza precedentemente indicati.

COMPENSAZIONE DELLE RETI

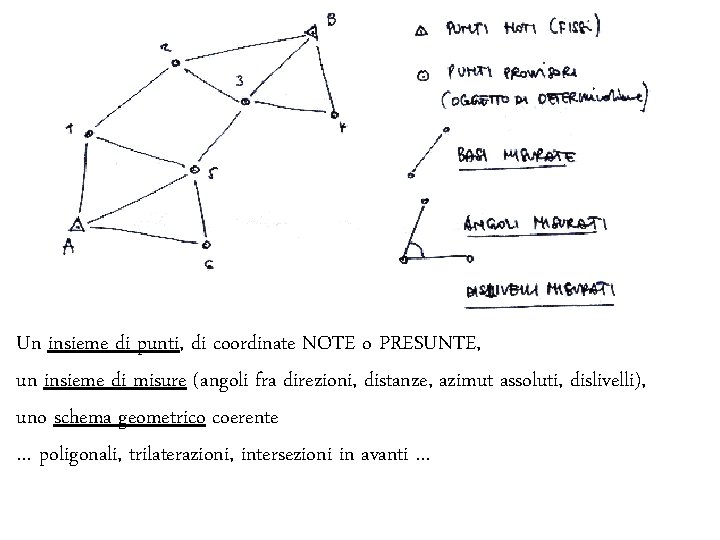
Un insieme di punti, di coordinate NOTE o PRESUNTE, un insieme di misure (angoli fra direzioni, distanze, azimut assoluti, dislivelli), uno schema geometrico coerente … poligonali, trilaterazioni, intersezioni in avanti …

Ripetizione - Compensazione Dopo la ripetizione delle misure principali si pone un calcolo che considera tutte le misurazioni insieme per definire le correzioni da apportare ai valori presunti x, y, z delle coordinate dei punti rilevati. La garanzia del risultato è tanto maggiore quanto cresce la ridondanza delle misure, cioè la differenza tra il numero delle grandezze osservate e il numero delle incognite.

Algoritmo di compensazione ai minimi quadrati LEGGE DEI MINIMI QUADRATI "In un sistema di osservazioni dello steso ordine di precisione, il valore più probabile Xo è quello che rende minima la somma dei quadrati degli scartidelle singole osservazioni Xi da Xo = Minimi

METODO DI COMPENSAZIONE 1. 2. 3. 4. 5. In un sistema di riferimento assegnato si calcolano dei valori provvisori per le coordinate x, y, z dei punti da determinare. Tali misure possono riguardare punti FISSI e/o PUNTI PROVVISORI 6. Ogni misura costituisce una EQUAZIONE

3. 4. 5. Ogni misura (EQUAZIONI) ha una sua precisione intrinseca espressa mediante il suo s. q. m. , precisione che costituisce il PESO statistico dell'equazione nel sistema complessivo. Ogni equazione del sistema esprime le relazioni tra la MISURA ESEGUITA di un elemento ed il valore di questa misura CALCOLATO dai valori provvisori di coordinate del punto: i due termini differiscono tra loro di una quantità, via decrescente detta: TERMINE NOTO DELLE EQUAZIONI GENERATE.

Organizzando i dati (misure, incognite) in forma matriciale, un sistema di equazioni di osservazione può essere scritto in forma compatta V = AX + L Dove V : Vettore dei residui di ogni equazione. A : Motrice dei coefficienti delle equazioni di osservazione. X : Vettore delle correzioni incognite (Xi, Ji, Xj, Jj) da applicare alle coordinate. L : Vettore dei termini noti di ogni equazione. Rappresenta la differenza tra il valore approssimato ed il valore misurato delle grandezze in gioco.

Matrice dei pesi Se le osservazioni non hanno la stessa precisione si deve introdurre il vettore (o matrice diagonale) dei pesi statitistici (s. q. m. ):

Vettore delle soluzioni La soluzione ai "minimi quadrati" per la ricerca del vettore delle soluzioni X si ottiene applicando le condizioni di minimo VTPV = MINIMO all'equazione V = AX + L.

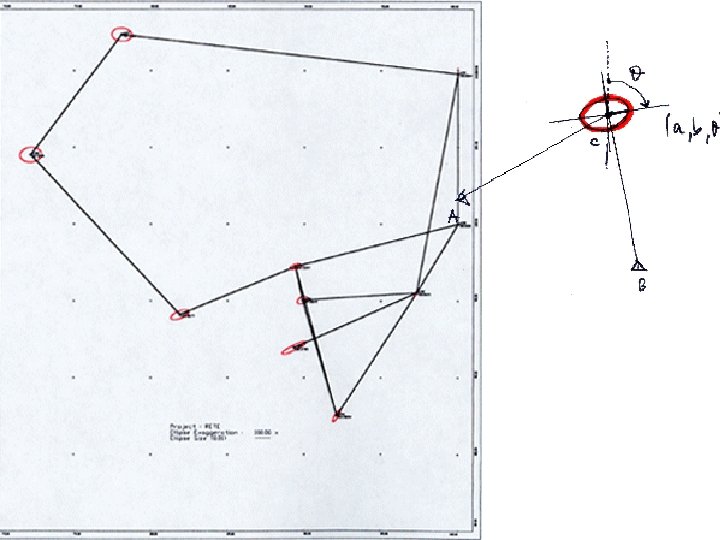
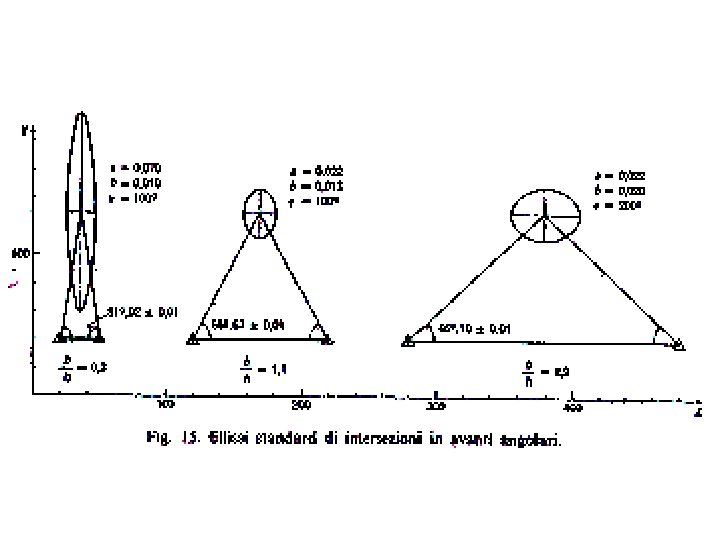
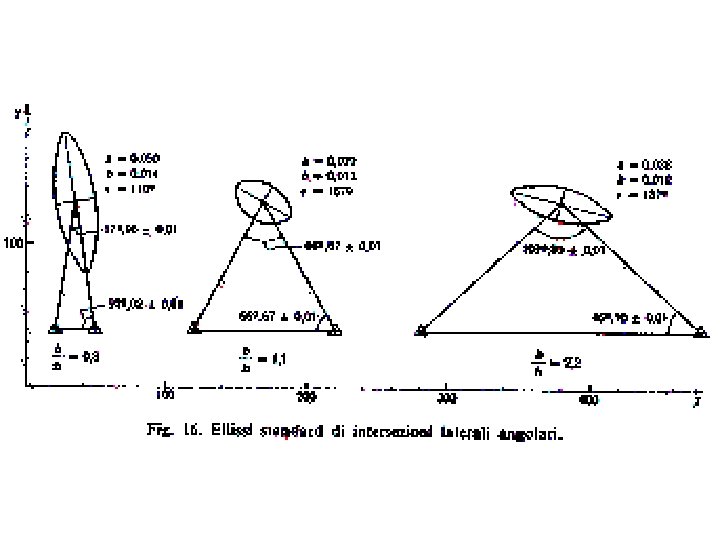
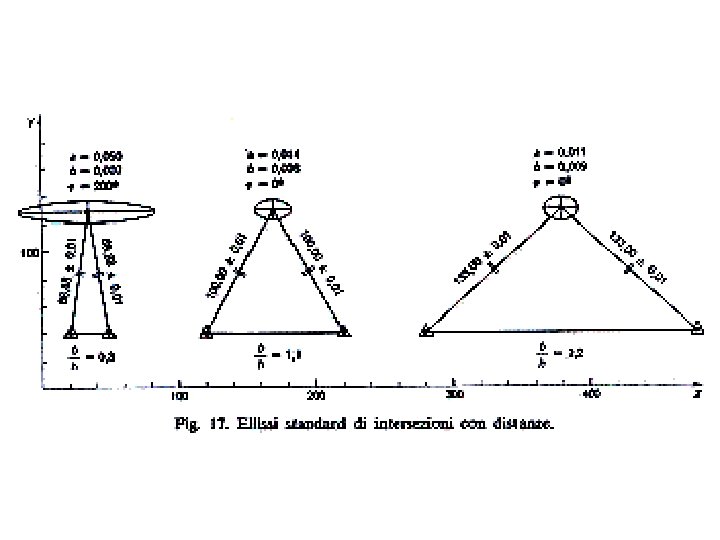
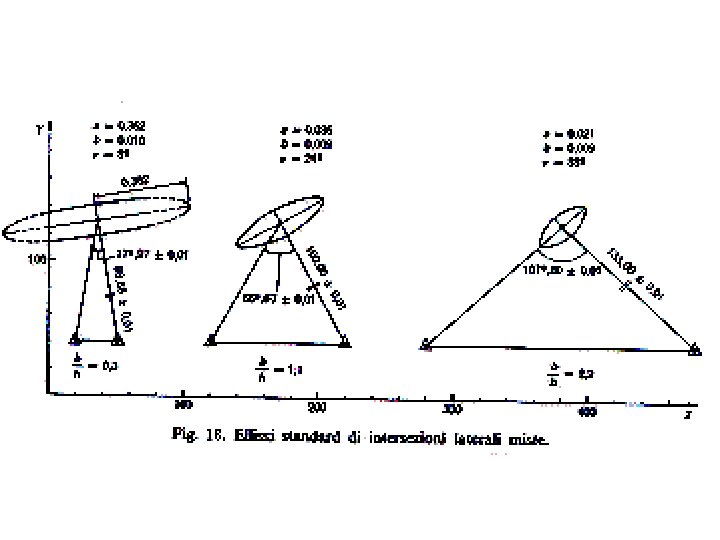
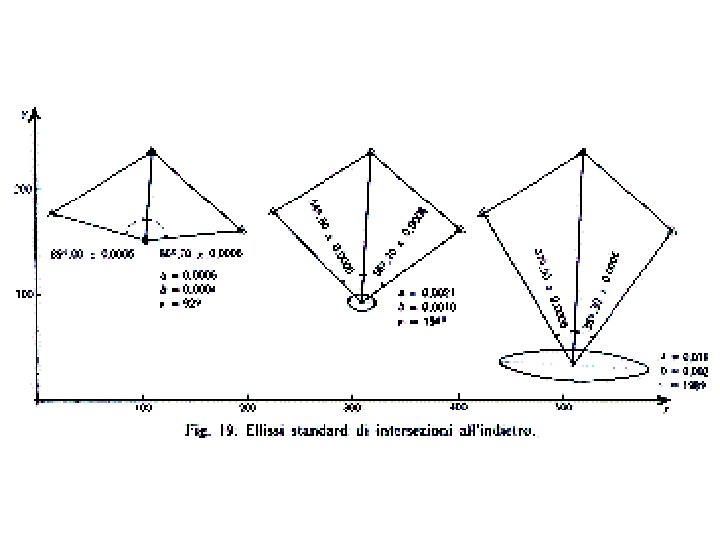
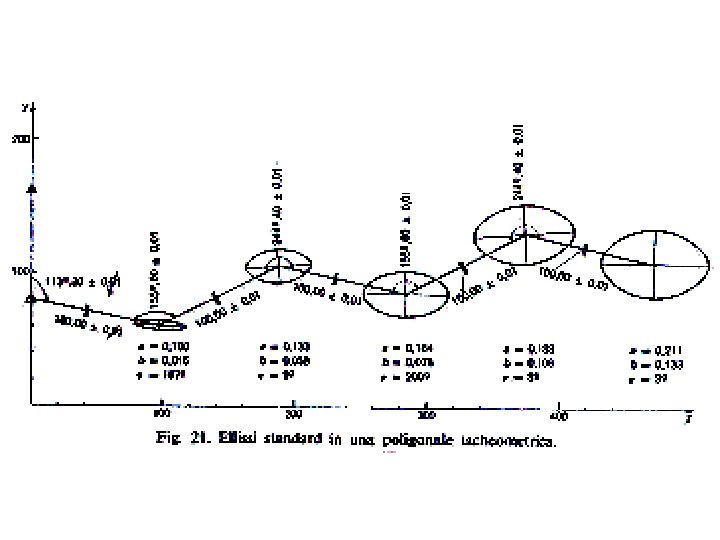
ELLISSE D’ERRORE La dispersione specifica dell’errore è espressivamente rappresentata dall'ellisse d'errore associata a un punto; è un diagramma che indica: • posizione del punto • incertezza del punto • direzioni privilegiate di propagazione dell'errore

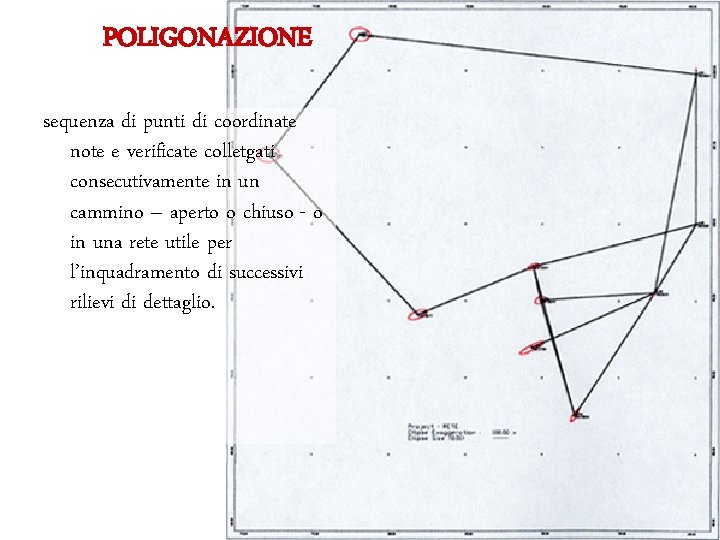
POLIGONAZIONE sequenza di punti di coordinate note e verificate colletgati consecutivamente in un cammino – aperto o chiuso - o in una rete utile per l’inquadramento di successivi rilievi di dettaglio.

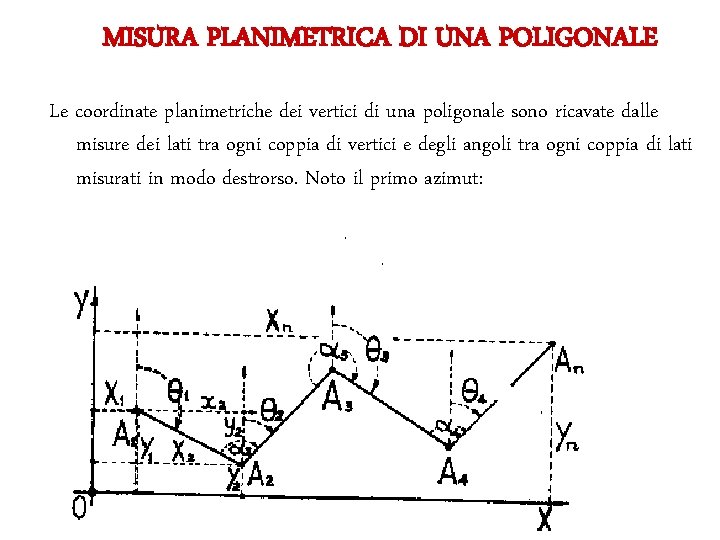
MISURA PLANIMETRICA DI UNA POLIGONALE Le coordinate planimetriche dei vertici di una poligonale sono ricavate dalle misure dei lati tra ogni coppia di vertici e degli angoli tra ogni coppia di lati misurati in modo destrorso. Noto il primo azimut:

COMPENSAZIONE ANGOLARE EMPIRICA Per la verifica angolare deve risultare la sommatoria degli n angoli interni di una poligonale chiusa: Qualora la differenza (errore di chiusura angolare) non superi il valore della tolleranza ammissibile, viene compensato distribuendo la sua aliquota per somma algebrica su tutti gli angoli. In caso contrario si devono rifare le misure.

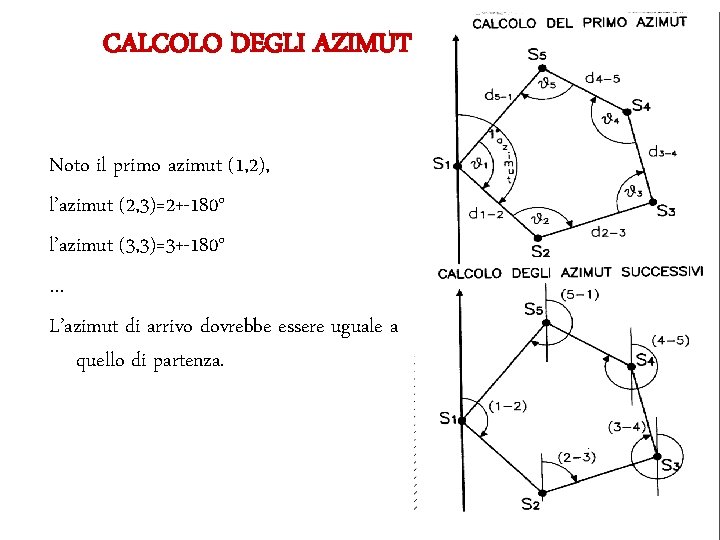
CALCOLO DEGLI AZIMUT Noto il primo azimut (1, 2), l’azimut (2, 3)=2+-180° l’azimut (3, 3)=3+-180° … L’azimut di arrivo dovrebbe essere uguale a quello di partenza.

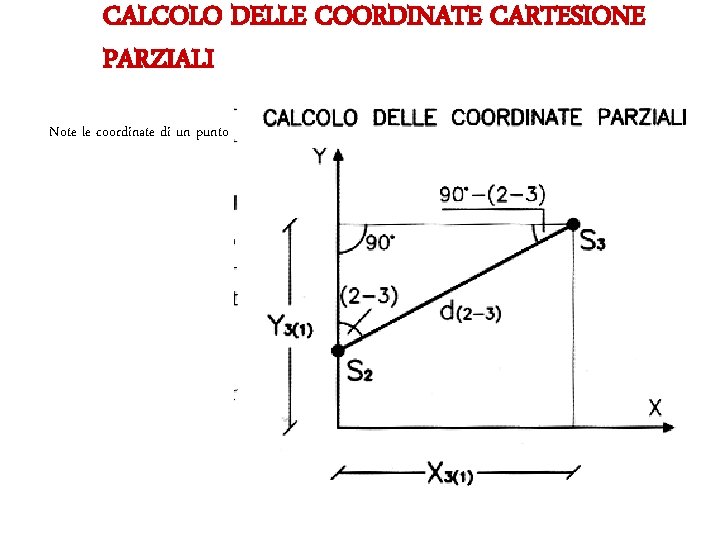
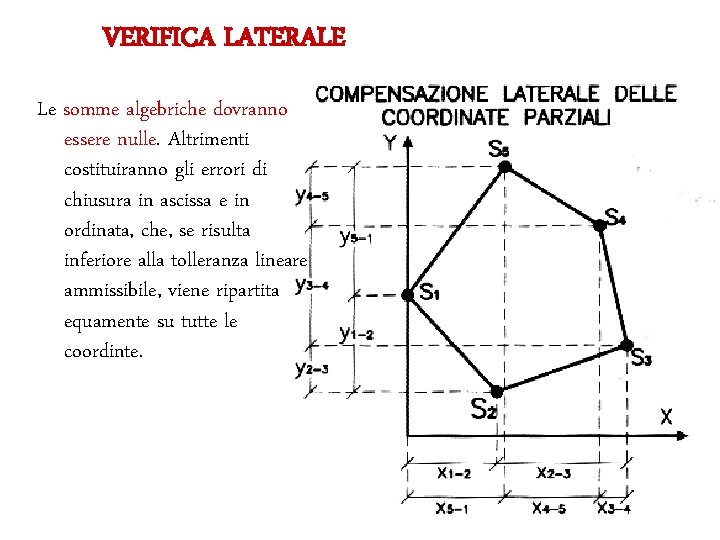
CALCOLO DELLE COORDINATE CARTESIONE PARZIALI Note le coordinate di un punto

VERIFICA LATERALE Le somme algebriche dovranno essere nulle. Altrimenti costituiranno gli errori di chiusura in ascissa e in ordinata, che, se risulta inferiore alla tolleranza lineare ammissibile, viene ripartita equamente su tutte le coordinte.

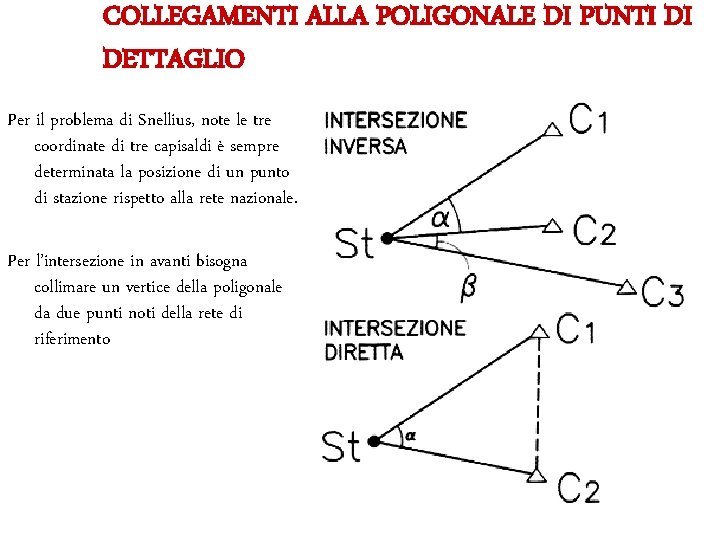
COLLEGAMENTI ALLA POLIGONALE DI PUNTI DI DETTAGLIO Per il problema di Snellius, note le tre coordinate di tre capisaldi è sempre determinata la posizione di un punto di stazione rispetto alla rete nazionale. Per l’intersezione in avanti bisogna collimare un vertice della poligonale da due punti noti della rete di riferimento

Il metodo topografico 1. 2. 3. 4. 5. 6. 7. 8. La topografia classica Il punto referente e i punti cartografici Misura degli angoli di direzione Angoli e distanze: la stazione totale Metodi mensori Morfologia delle reti Simulazione dell’incertezza livellazioni

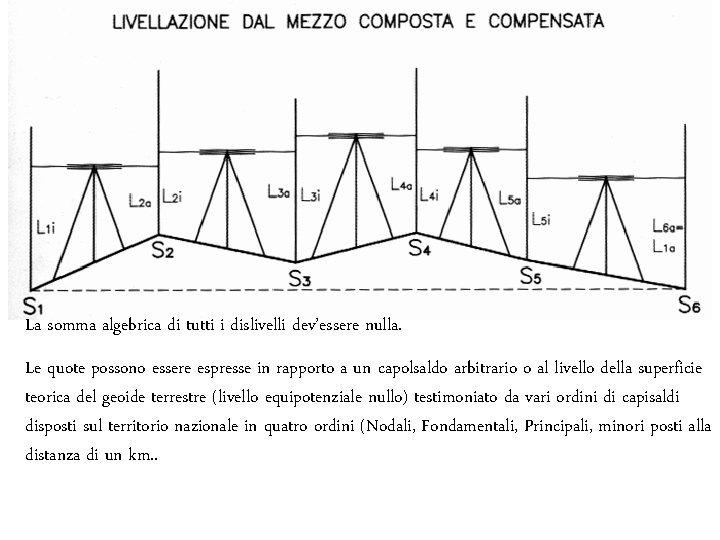
LIVELLAZIONI DI UNA POLIGONALE CHIUSA Individuazione dei dislivelli tra i vertici. • Con visuale orizzontale o livellazione geometrica • Da un estremo • Dal mezzo • Con visuale inclinata o livellazione trigonometrica. § Da un estremo § Reciproca • Senza visuale (ad es. barometrica)

La somma algebrica di tutti i dislivelli dev’essere nulla. Le quote possono essere espresse in rapporto a un capolsaldo arbitrario o al livello della superficie teorica del geoide terrestre (livello equipotenziale nullo) testimoniato da vari ordini di capisaldi disposti sul territorio nazionale in quatro ordini (Nodali, Fondamentali, Principali, minori posti alla distanza di un km. .