IKTi SUprosjektet Matlab som verkty i prosesstenkikk IKTi

IKTi. SU-prosjektet: Matlab som verktøy i prosesstenkikk IKTi. SU seminar NTNU 15/10 2014 Øyvind Gregersen

TKP 4120 Prosessteknikk • Ca 170 studenter, hvorav – 115 fra Industriell kjemi og bioteknologi 1. årskurs, – 20 fra Petroleumsteknologi 3. årkurs – 5 fra Kybernetikk 3. årskurs • Resten tar emnet som gjentak eller frivillig gjentak • Dette er første møte med kjemiteknikk for MTKJ 2

Bakgrunn • IKTi. SU, Hva er det? • http: //www. ntnu. no/studier/iktisu • Et prosjekt ved NTNU som bevilger midler til prosjekter som har: • Utviklet læremateriell for IKT i undervisning. • Tilpasset emner for faglig bruk av IKT. – Prosjekt som omfatter pedagogisk utvikling prioriteres fremfor utstyr- og programvareinnkjøp. Vi prioriterer prosjekt som etablerer "IKT-strenger" i emner, slik at studentene kan bygge videre på grunnlaget fra IT-grunnkurs. 3

Faglig innhold og læringsmål 4 • • Faglig innhold Tilstandsfunksjoner, ideell gass og reell gass. Termodynamikkens 1. og 2. lov, termokjemi, entropi, indre energi, entalpi, Gibbs fri energi, likevekt. Eksempler på industrielle prosesser og hvilke beregninger som trengs i disse. Åpne og lukkede systemer. Likevekt. Grunnleggende massebalanser. Massebalanser med reaksjon, enkle reaksjoner, komplekse reaksjonsskjemaer, reaksjonsomfang. Energibalanser, bidrag til energiligningen fra mekanisk energi og varme. Bruk av regneverktøy. • • Læringsmål Etter endt emne skal studentene kunne: - Gjøre rede for hvordan masse og energibalanseres i et stasjonært system. - Bruke termodynamikkens 1. og 2. lov sammen med massebalanser og likevektberegninger til å finne likevektsammensetning ut av en reaktor. - Sette opp og løse et ligningssystem av masse og energibalanser for en stasjonær prosess med reaksjon, separasjon og resirkulasjon. - Kunne gjøre kvantitative beregninger av masse og energibalanser av stasjonere kjemiske prosesser. - Kunne gjøre enkle simuleringer av masse og energibalanser av stasjonere kjemiske prosesser. - Dimensjonere arealet til en varmeveksler. - Beregne varme/kjøleeffekt og energiforbruk i en varmepumpe eller kjølemaskin. - Bruke energi og massebalanser til å gjøre stasjonære beregninger av turbiner, pumper, ventiler, flash, varmeveksler, splitt, blanding, varmepumpe, kjølemaskin og reaktor. - Ha detaljert kunnskap om minst en industriell prosess fra Norsk prosessindustri.

Prosjektet for Prosessteknikk • Total prosjektramme på 244 kkr • Av dette er 150 kkr midler fra IKTi. SU • 94 kkr er egeninnsats (arbeid) fra IKP • Innsats i prosjektet – – 5 2 månedsverk ekstra fra vit. ass. (Camilla Berge Vik ) 2 ekstra studentassistenter (Kasper Linnestad og Kjetil Sonerud ) Matlab og programeringshjelp fra Brian Grimes Prosjektledelse og faglig ledelse fra Øyvind

Hva er gjort? • Vi forsøker å bygge på matlabferdigheter fra IKT grunnkurs • Lagt inn ca 50% oppgaver som må løses i matlab i øving 2 -10 (dvs 9 av 11 øvinger) • Omarbeidet prosjektoppgavene (metanol og CO 2 -absorbsjon) slik at Matlab brukes som regneverktøy. • Evaluering av matlabøvinger med stud. ass. og vit. ass. • Evaluering i referansegruppemøter • Evaluering i spørreundersøkelse • Justering av opplegget basert på evaluering er under arbeid 6

Øvinger Planlagt øvingsopplegg: • • • • 7 Uke nr. 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Øving nr. 1 2 3 4 5 6 7 8 9 10 11 Emne Massebalanser og Ideell gass P, V, T og Tilstandsligninger 1. lov, Tilstandsligning og Massebalanse Likevekt, resirkulasjon Energibalanse, resirkulasjon med avtapp Masse- og energibalanse metanol, Cp(T) Varmebalanse, simulering av varmeveksler Reell gass kompresjon, kjølesyklus ammoniakk Metanolreaktor, reaktor med to koblede likevekter Kjølesyklus Prosjektarbeid ++ Prosjektarbeid++ Påske

Konkret innhold i øvingene • M 1: Ideell gasslov – Lag en funksjon som returnerer trykk som skalar gitt input T, R, V og n som skalarer. – Modifiser funksjonen til å returnere en vektor gitt at V er en vektor og R, T og n er skalarer – Lag et plot der p er en funksjon av V, sett navn på aksene • M 2: Ideell gasslov II – Importer et datasett med P, V, n og T vha «importdata» – Strukturer datasettet som matrise – Plott reelle trykkdata mot ideelt trykk (beregnet med funksjonen fra M 1) – Regn ut R for hvert enkelt sett av P, V, n, T og plot beregnet R som funksjon av P 8

Innhold i øvingene, forts. • M 3 van der Waals tilstandsligning – – Lag en funksjon som returnerer P Lag en funksjon som returnerer parameteren a Importer et datasett av P og T, beregn a. Plot a som funksjon av T Importer et nytt datasett, beregn ideelt trykk, vd. W-trykk. Plott reelt trykk, ideelt trykk og vd. W-trykk som funksjon av volum • M 4 Massebalanser for dehydrogenering av propan – Massebalanse over en reaktor og separator på vektorform • M 5 Massebalanser II – Systemet fra M 4 utvides med en resirkulasjonsstrøm. Alle massebalanser formuleres på vektorform. Løses som lineær matrise x=A/b (inv(A)*b) 9

Innhold i øvingene, forts. 10 • M 6 – Ammoniakkproduksjon med reaktor, separator og resirk. – Formuler massebalanser og løs med ulike splittfaktorer. Plot mengde inert (metan) inn i reaktor som funksjon av splittfaktor. • M 7 – Varmekapasitet som funksjon av temperatur – Lag en funksjon som returnerer en vektor av varmekapasiteter for 5 ulike komponenter ved en gitt inputtemperatur. – Plot Cp(T) for hver av komponentene i intervallet 300 -600 K – Lag en funksjon som returnerer midlere varmekapasitet for en blanding av komponenter (xi er input) i et temperaturintervall (T 1 og T 2 er input) • M 8 – Simulering av varmeveksler – Formuler ligningene når U*A, Tinn og m er kjent. Finn Q og Tut ved å løse koblede ikke-lineære ligninger med «fsolve» . – Varier mc, inn og plott Th, ut, Tc, ut og Q som funksjon av mc, inn

Innhold i øvingene, forts. • M 9 – Isoterm og adiabatisk kompresjon – Lag en funksjon som returnerer virkelig arbeid ved isoterm kompresjon og en som returnerer virkelig arbeid ved adiabatisk kompresjon. Begge skal ha molstrøm og alle nødvendige parametere som input. – Funksjonene brukes til å løse noen konkrete oppgaver. • M 10 – Metanolreaksjon med to likevekter – For å løse massebalansene over reaktoren må to ikke-lineære ligninger løses. «fsolve» brukes til dette 11

Statoil Tjeldbergodden (Nordmøre) 12

Sintef • CO 2 -fangst • Flerfasestrømning • Lab 13

Prosjektoppgavene • 3 uker med prosjektarbeid – Masse og energibalanser for henholdsvis metanolprosessen og CO 2 -absorbsjon - Matlab er obligatorisk regneverktøy som brukes til: - Massebalanser for hele prosessen - Entalpiberegninger - Kompressorberegninger 14

Sammendrag • Studentene bruker: – Lærer god programeringsskikk (variabelnavn, bruk av kommentarer etc) – Plotting – Import av data – Lærer å bruke funksjoner – Løser lineære ligninger med matriseregning – Løser ikkelineære ligninger med f-solve eller iterasjon (metanolprosjektet) 15
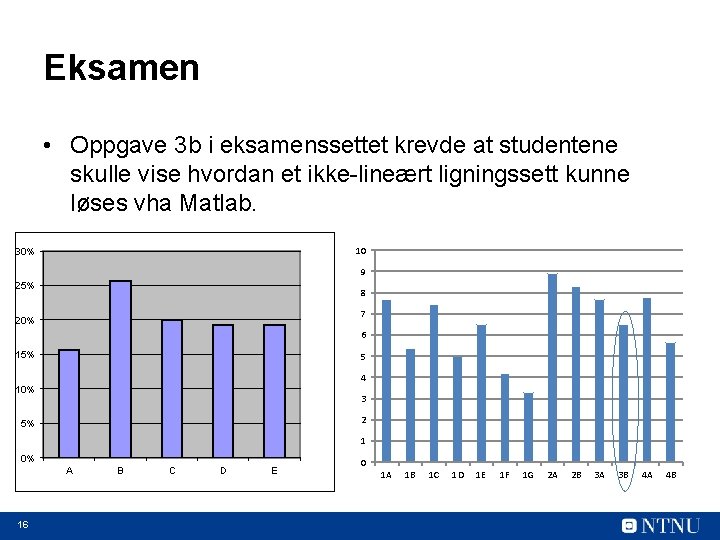
Eksamen • Oppgave 3 b i eksamenssettet krevde at studentene skulle vise hvordan et ikke-lineært ligningssett kunne løses vha Matlab. 10 30% 9 25% 8 7 20% 6 15% 5 4 10% 3 2 5% 1 0% A 16 B C D E 0 1 A 1 B 1 C 1 D 1 E 1 F 1 G 2 A 2 B 3 A 3 B 4 A 4 B

Videre arbeid • Revisjon av øvingsopplegget fra 2014 – omfanget må noe ned. • Øke fra 3 til 4 timer med dedikert matlabforelesning • Løsningsforslag matlab – to versjoner – «Denne løsningen er skikkelig god» og «dette er den enkleste måten som fungerer» • Undervisningsrom – Bør absolutt ha undervisningsrom med mye stikkontakter til øvingsunervisning • Veiledning – Veiledning i programmering er mer arbeidskrevende enn veiledning i ordinære regneøvinger. => Emnet trenger 1 -2 ekstra studentassistenter 17

Videre arbeid II • Emnet TKP 4120 Strømning og Varmetransport (2. årskur for MTKJ) revideres nå slik at bruk av regneverktøy i dette emnet bygger på det som har blitt gjort i Prosessteknikk. 18
- Slides: 18