IIR Infinite Impulse Response is the angular frequency

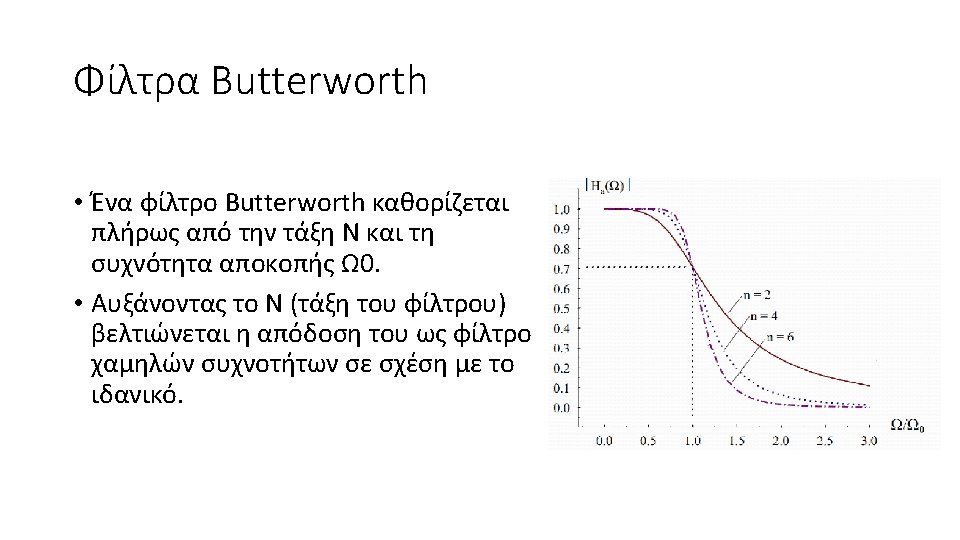
φίλτρα IIR (Infinite Impulse Response) ω is the angular frequency in radians per second and n is the number of poles in the filter The frequency response plot from Butterworth's 1930 paper

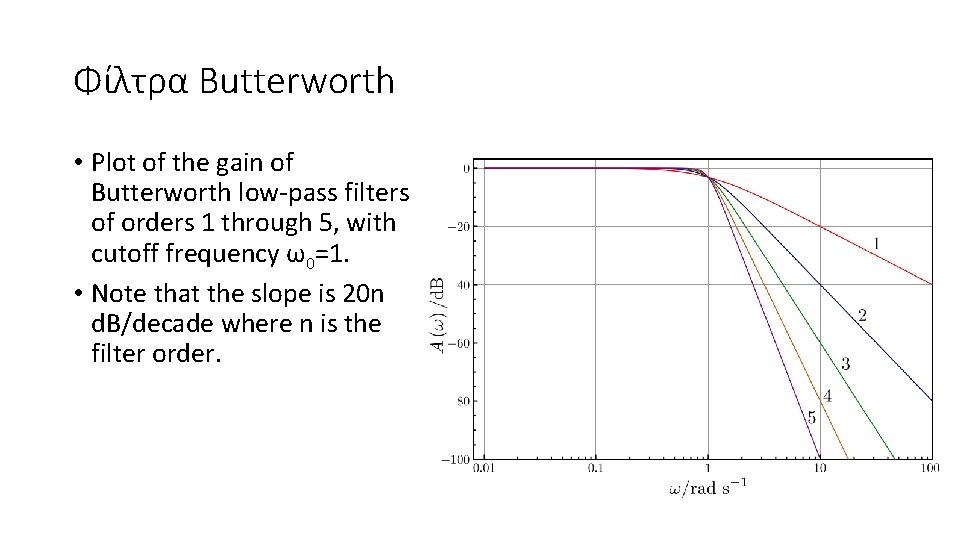
Φίλτρα Butterworth • Plot of the gain of Butterworth low-pass filters of orders 1 through 5, with cutoff frequency ω0=1. • Note that the slope is 20 n d. B/decade where n is the filter order.

Κατασκευή φίλτρων Butterworth • [b, a] = butter(n, Wn) returns the transfer function coefficients of an nth-order lowpass digital Butterworth filter with normalized cutoff frequency Wn. • example • [b, a] = butter(n, Wn, ftype) designs a lowpass, highpass, bandpass, or bandstop Butterworth filter, depending on the value of ftype and the number of elements of Wn. The resulting bandpass and bandstop designs are of order 2 n. • Filter type, specified as one of the following: • 'low' specifies a lowpass filter with cutoff frequency Wn. 'low' is the default for scalar Wn. • 'high' specifies a highpass filter with cutoff frequency Wn. • 'bandpass' specifies a bandpass filter of order 2 n if Wn is a two-element vector. 'bandpass' is the default when Wn has two elements. • 'stop' specifies a bandstop filter of order 2 n if Wn is a two-element vector.

Κατασκευή φίλτρων Butterworth • Design a 6 th-order Butterworth bandstop filter with normalized edge frequencies of 0. 2π and 0. 6π rad/sample. Plot its magnitude and phase responses. Use it to filter random data. • • • [b, a] = butter(3, [0. 2 0. 6], 'stop'); freqz(b, a) data. In = randn(1000, 1); data. Out = filter(b, a, data. In); https: //www. mathworks. com/help/signal/ref/butter. html https: //en. wikipedia. org/wiki/Butterworth_filter

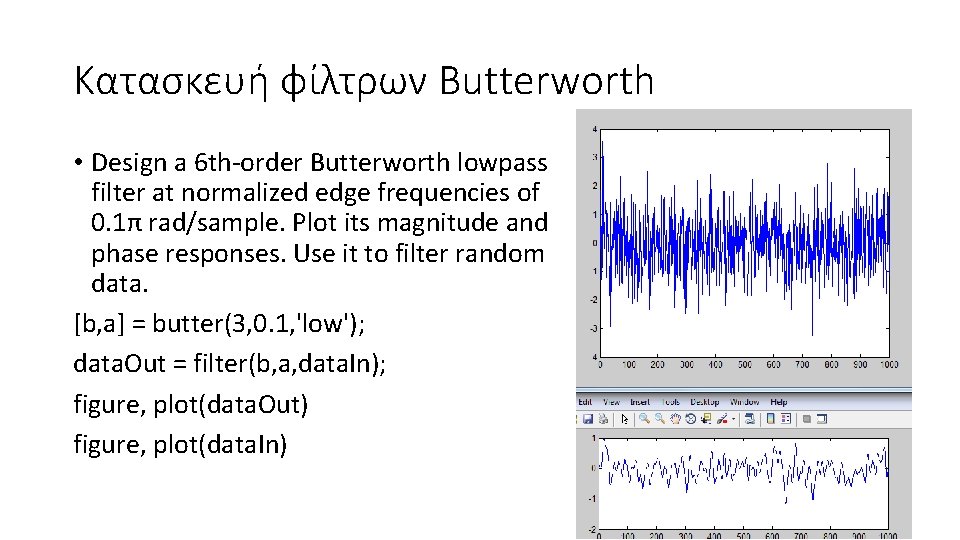
Κατασκευή φίλτρων Butterworth • Design a 6 th-order Butterworth lowpass filter at normalized edge frequencies of 0. 1π rad/sample. Plot its magnitude and phase responses. Use it to filter random data. [b, a] = butter(3, 0. 1, 'low'); data. Out = filter(b, a, data. In); figure, plot(data. Out) figure, plot(data. In)

• Design a 6 th-order lowpass Butterworth filter with a cutoff frequency of 300 Hz, which, for data sampled at 1000 Hz, corresponds to 0. 6 rad/sample. Plot its magnitude and phase responses. Use it to filter a 1000 -sample random signal. • fc = 300; • fs = 1000; • [b, a] = butter(6, fc/(fs/2)); • freqz(b, a)