III Turbo Codes Applications of Turbo Codes Worldwide

III. Turbo Codes

Applications of Turbo Codes Worldwide Applications & Standards l Data Storage Systems l DSL Modem / Optical Communications l 3 G (Third Generation) Mobile Communications l Digital Video Broadcast (DVB) l Satellite Communications l IEEE 802. 16 Wi. MAX l … © Tallal Elshabrawy

Basic Concept of Turbo Codes Invented in 1993 by Alian Glavieux, Claude Berrou and Punya Thitimajshima Basic Structure: a) Recursive Systematic Convolutional (RSC) Codes b) Parallel concatenation and Interleaving c) Iterative decoding © Tallal Elshabrawy
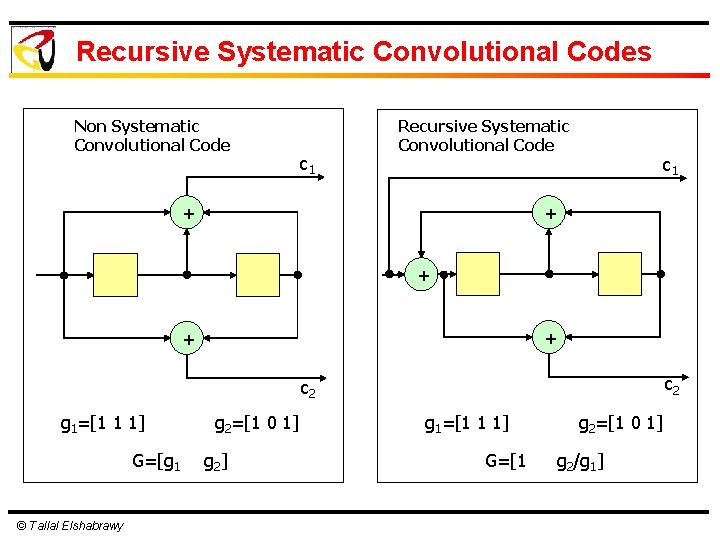
Recursive Systematic Convolutional Codes Non Systematic Convolutional Code c 1 Recursive Systematic Convolutional Code + c 1 + + c 2 g 1=[1 1 1] G=[g 1 © Tallal Elshabrawy g 2=[1 0 1] g 2 ] g 1=[1 1 1] G=[1 g 2=[1 0 1] g 2/g 1]
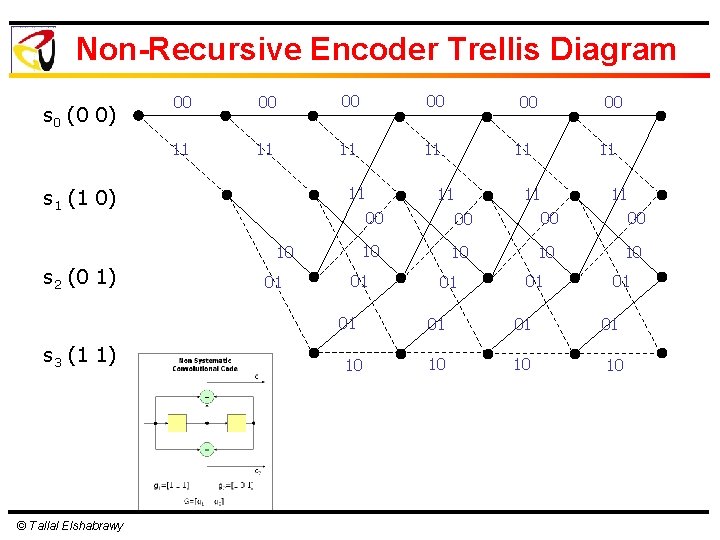
Non-Recursive Encoder Trellis Diagram s 0 (0 0) 00 00 11 11 11 s 1 (1 0) 10 s 2 (0 1) 01 © Tallal Elshabrawy 00 11 11 11 00 00 10 10 01 01 s 3 (1 1) 00 10 01 01 01 10 10 10
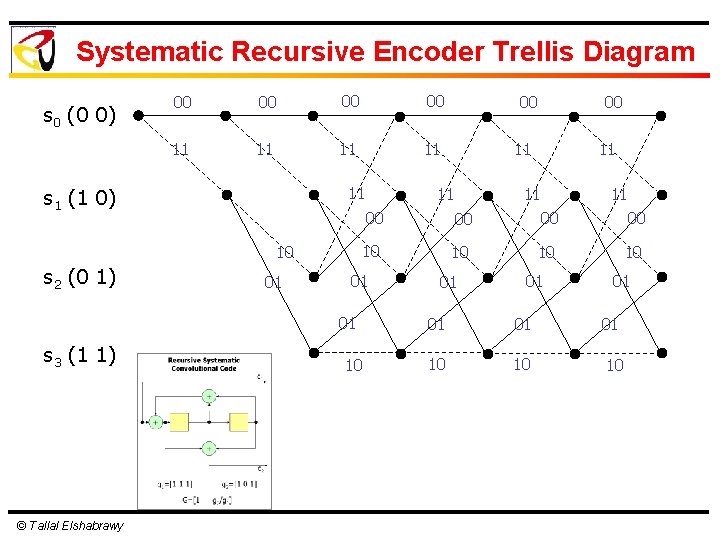
Systematic Recursive Encoder Trellis Diagram s 0 (0 0) 00 00 11 11 11 s 1 (1 0) 10 s 2 (0 1) 01 © Tallal Elshabrawy 00 11 11 11 00 00 10 10 01 01 s 3 (1 1) 00 10 01 01 01 10 10 10
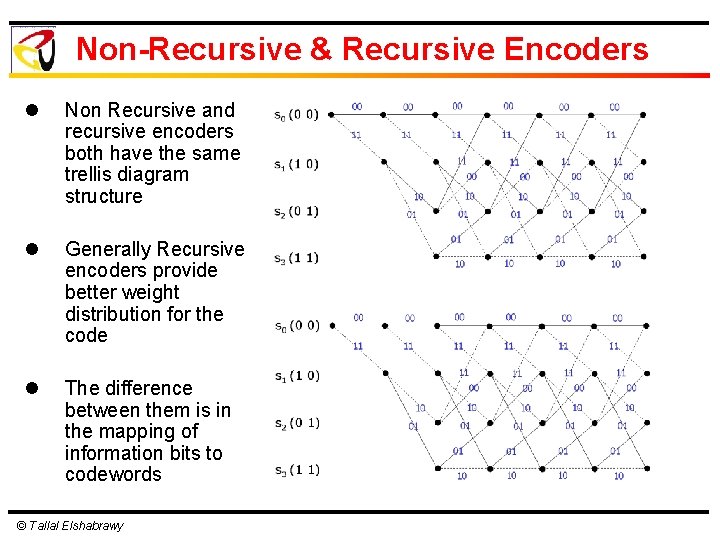
Non-Recursive & Recursive Encoders l Non Recursive and recursive encoders both have the same trellis diagram structure l Generally Recursive encoders provide better weight distribution for the code l The difference between them is in the mapping of information bits to codewords © Tallal Elshabrawy
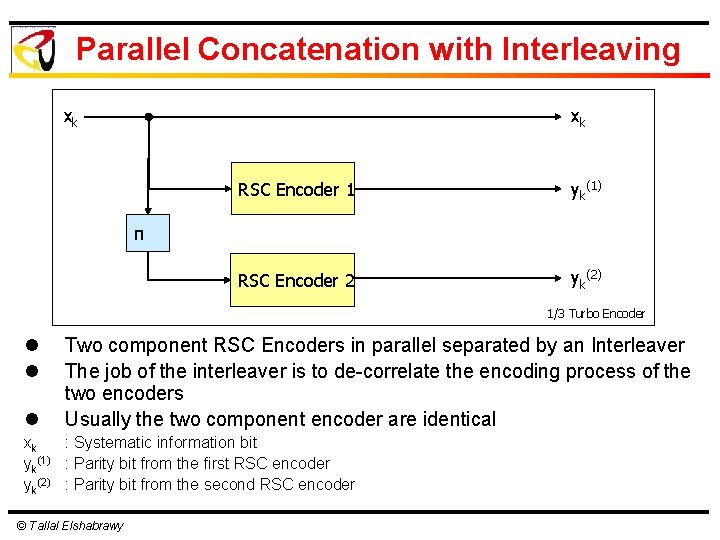
Parallel Concatenation with Interleaving xk xk RSC Encoder 1 yk(1) RSC Encoder 2 yk(2) π 1/3 Turbo Encoder l l l Two component RSC Encoders in parallel separated by an Interleaver The job of the interleaver is to de-correlate the encoding process of the two encoders Usually the two component encoder are identical xk : Systematic information bit yk(1) : Parity bit from the first RSC encoder yk(2) : Parity bit from the second RSC encoder © Tallal Elshabrawy

Interleaving Permutation of data to de-correlate encoding process of both encoders If encoder 1 generates a low weight codeword then hopefully the interleaved input information would generate a higher weight codeword By avoiding low weight codewords the BER performance of the turbo codes could improve significantly © Tallal Elshabrawy
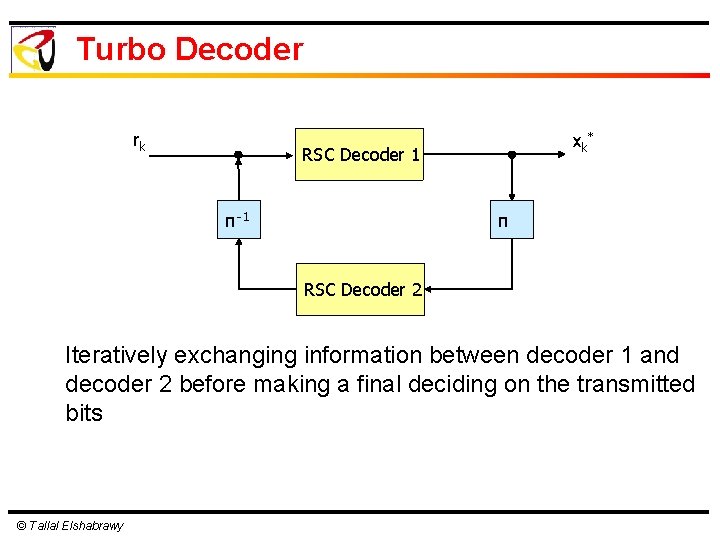
Turbo Decoder rk xk* RSC Decoder 1 π-1 π RSC Decoder 2 Iteratively exchanging information between decoder 1 and decoder 2 before making a final deciding on the transmitted bits © Tallal Elshabrawy
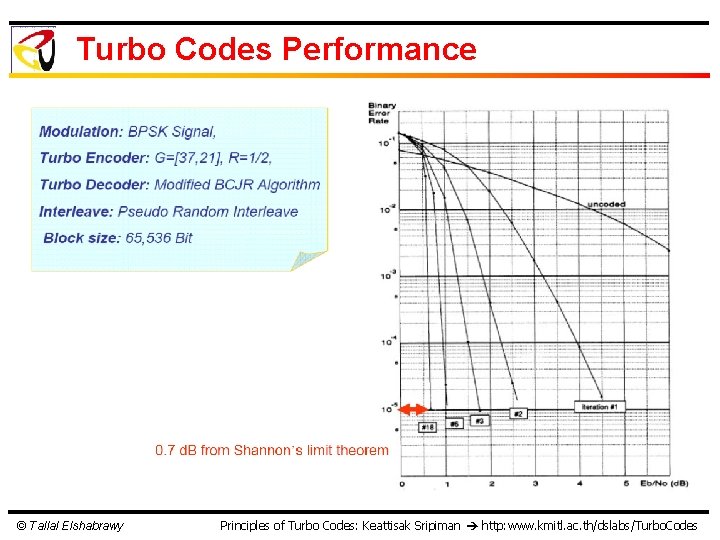
Turbo Codes Performance © Tallal Elshabrawy Principles of Turbo Codes: Keattisak Sripiman http: www. kmitl. ac. th/dslabs/Turbo. Codes

Turbo Decoding l Turbo decoders rely on probabilistic decoding of component RSC decoders l Iteratively exchanging soft-output information between decoder 1 and decoder 2 before making a final deciding on the transmitted bits l As the number of iteration grows, the decoding performance improves © Tallal Elshabrawy 12
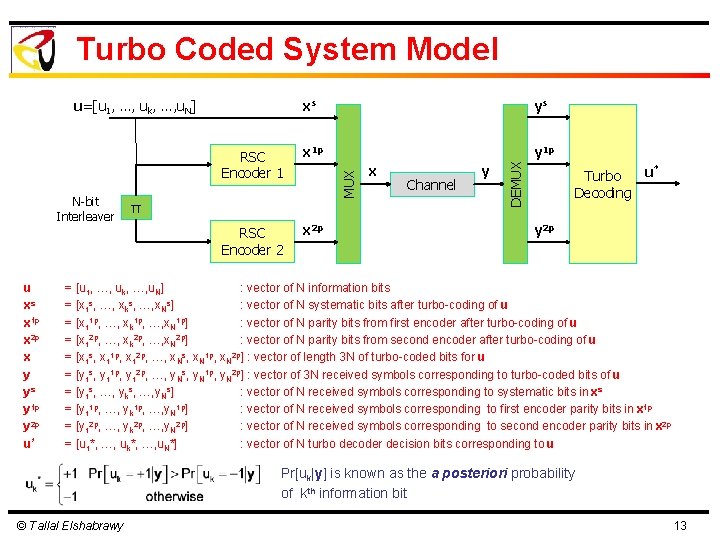
Turbo Coded System Model RSC Encoder 1 x 1 p y 1 p N-bit Interleaver RSC Encoder 2 x 2 p u xs x 1 p x 2 p x y ys y 1 p y 2 p u* π x Channel y DEMUX ys MUX xs u=[u 1, …, uk, …, u. N] u* Turbo Decoding y 2 p = [u 1, …, uk, …, u. N] : vector of N information bits s = [x 1 , …, xk , …, x. N ] : vector of N systematic bits after turbo-coding of u 1 p 1 p 1 p = [x 1 , …, xk , …, x. N ] : vector of N parity bits from first encoder after turbo-coding of u = [x 12 p, …, xk 2 p, …, x. N 2 p] : vector of N parity bits from second encoder after turbo-coding of u = [x 1 s, x 11 p, x 12 p, …, x. Ns, x. N 1 p, x. N 2 p] : vector of length 3 N of turbo-coded bits for u = [y 1 s, y 11 p, y 12 p, …, y. Ns, y. N 1 p, y. N 2 p] : vector of 3 N received symbols corresponding to turbo-coded bits of u = [y 1 s, …, yks, …, y. Ns] : vector of N received symbols corresponding to systematic bits in xs = [y 11 p, …, yk 1 p, …, y. N 1 p] : vector of N received symbols corresponding to first encoder parity bits in x 1 p = [y 12 p, …, yk 2 p, …, y. N 2 p] : vector of N received symbols corresponding to second encoder parity bits in x 2 p = [u 1*, …, uk*, …, u. N*] : vector of N turbo decoder decision bits corresponding to u Pr[uk|y] is known as the a posteriori probability of kth information bit © Tallal Elshabrawy 13

Log-Likelihood Ratio (LLR) The LLR of an information bit uk is given by: Given that Pr[uk=+1]+Pr[uk=-1]=1 © Tallal Elshabrawy 14
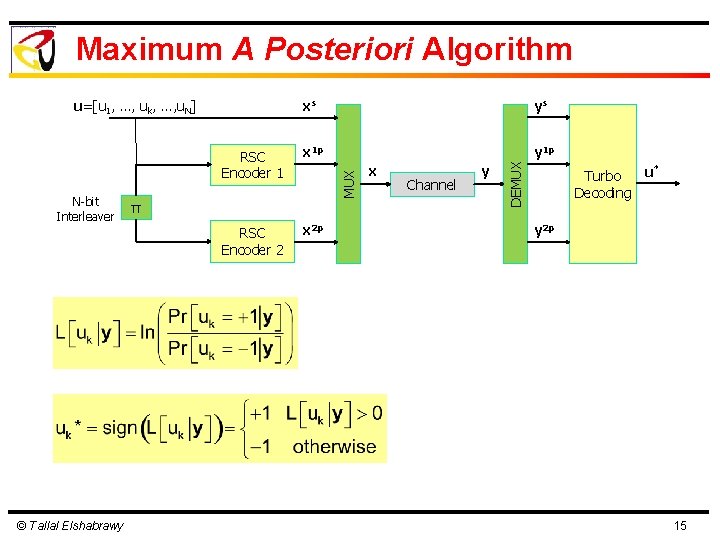
Maximum A Posteriori Algorithm RSC Encoder 1 x 1 p y 1 p N-bit Interleaver RSC Encoder 2 x 2 p © Tallal Elshabrawy π x Channel y DEMUX ys MUX xs u=[u 1, …, uk, …, u. N] u* Turbo Decoding y 2 p 15
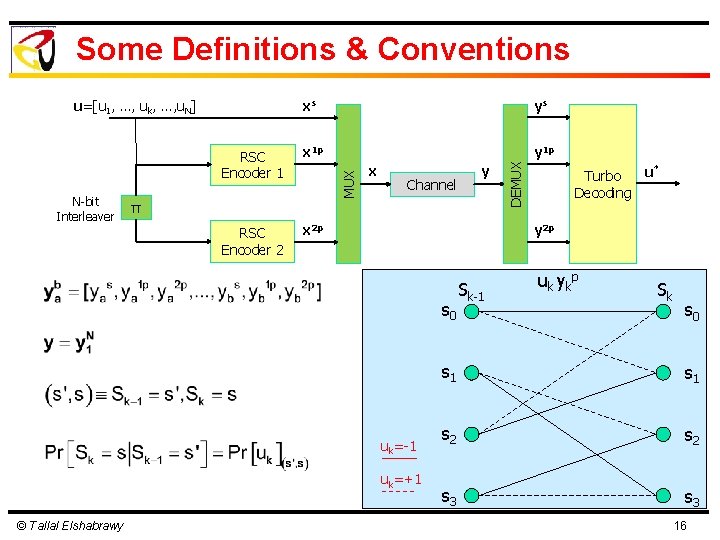
Some Definitions & Conventions RSC Encoder 1 x 1 p y 1 p N-bit Interleaver RSC Encoder 2 x 2 p x Channel π u* Turbo Decoding y 2 p s 0 uk=-1 uk=+1 © Tallal Elshabrawy y DEMUX ys MUX xs u=[u 1, …, uk, …, u. N] Sk-1 uk ykp Sk s 0 s 1 s 2 s 3 16
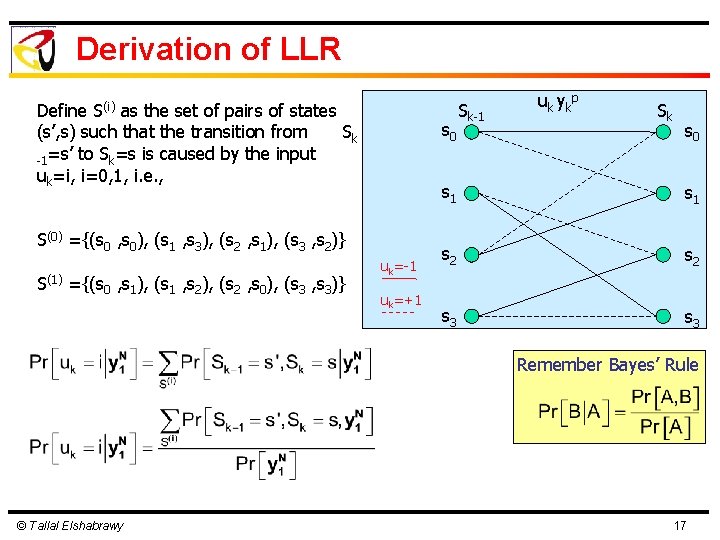
Derivation of LLR S(i) Define as the set of pairs of states (s’, s) such that the transition from Sk -1=s’ to Sk=s is caused by the input uk=i, i=0, 1, i. e. , s 0 S(0) ={(s 0 , s 0), (s 1 , s 3), (s 2 , s 1), (s 3 , s 2)} S(1) ={(s 0 , s 1), (s 1 , s 2), (s 2 , s 0), (s 3 , s 3)} uk=-1 uk=+1 Sk-1 uk ykp Sk s 0 s 1 s 2 s 3 Remember Bayes’ Rule © Tallal Elshabrawy 17
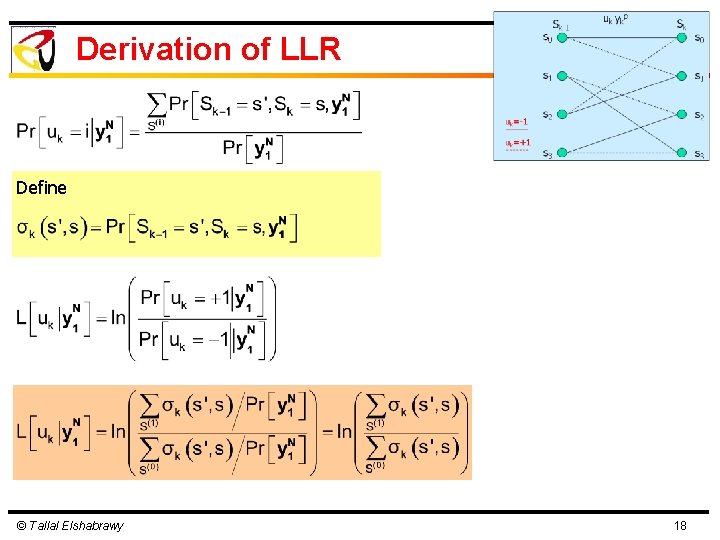
Derivation of LLR Define © Tallal Elshabrawy 18
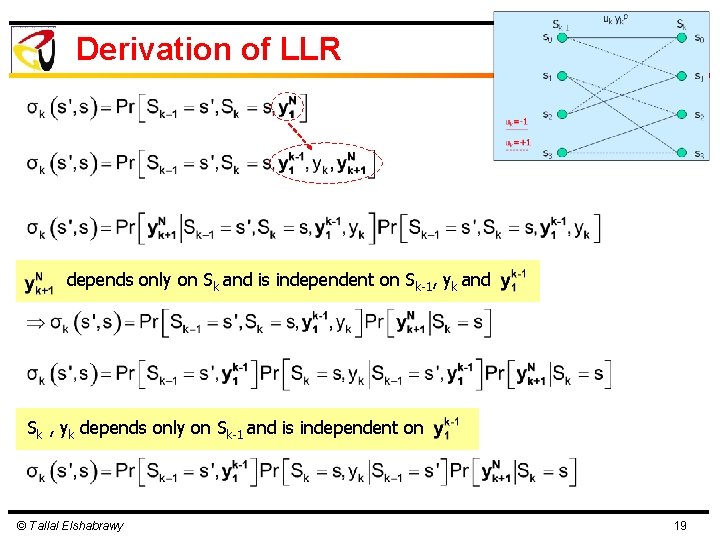
Derivation of LLR depends only on Sk and is independent on Sk-1, yk and Sk , yk depends only on Sk-1 and is independent on © Tallal Elshabrawy 19

Derivation of LLR © Tallal Elshabrawy 20
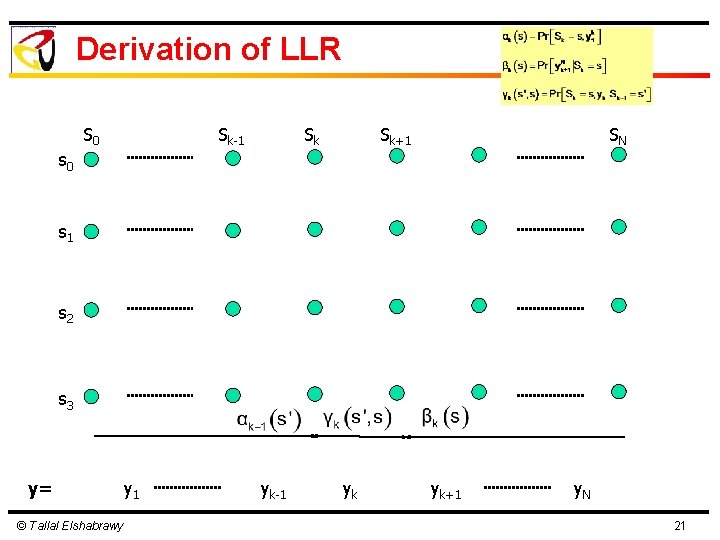
Derivation of LLR S 0 Sk-1 Sk Sk+1 SN s 0 s 1 s 2 s 3 y= © Tallal Elshabrawy y 1 yk-1 yk yk+1 y. N 21
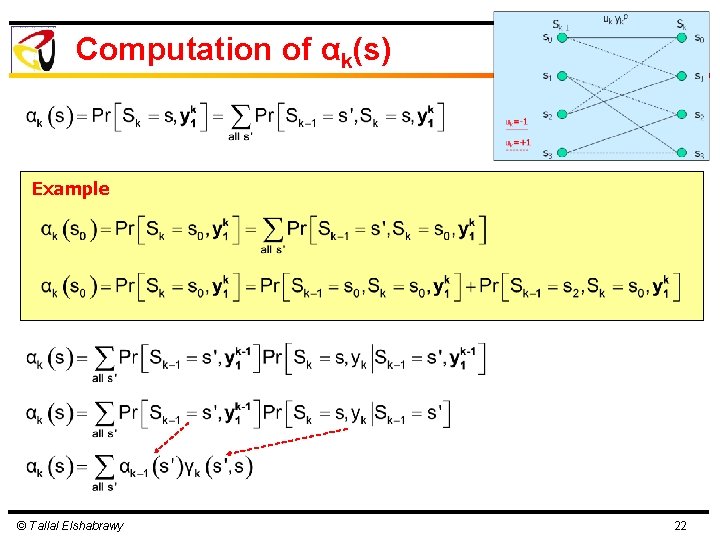
Computation of αk(s) Example © Tallal Elshabrawy 22

Computation of αk(s) Forward Recursive Equation Given the values of γk(s’, s) for all index k, the probability αk(s) can be forward recursively computed. The initial condition α 0(s) depends on the initial state of the convolutional encoder The encoder usually starts at state 0 © Tallal Elshabrawy 23

Computation of βk(s) Backward Recursive Equation Given the values of γk(s’, s) for all index k, the probability βk(s) can be backward recursively computed. The initial condition βN(s) depends on the final state of the trellis First encoder usually finishes at state s 0 Second encoder usually has open trellis © Tallal Elshabrawy 24

Computation of γk(s’, s) Note that © Tallal Elshabrawy 25
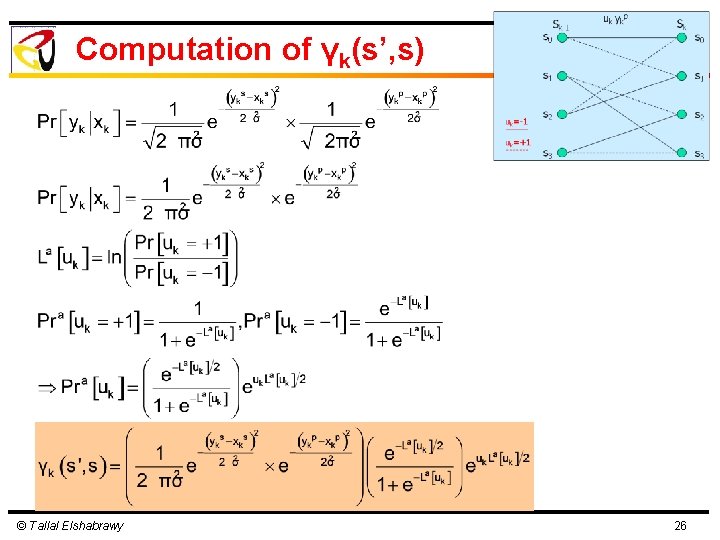
Computation of γk(s’, s) © Tallal Elshabrawy 26
- Slides: 26