III Strain and Stress Basics of continuum mechanics

III. Strain and Stress • Basics of continuum mechanics, Strain • Basics of continuum mechanics, Stress Reading Suppe, Chapter 3 Twiss&Moores, chapter 15 Additional References : Jean Salençon, Handbook of continuum mechanics: general concepts, thermoelasticity, Springer, 2001 Chandrasekharaiah D. S. , Debnath L. (1994) Continuum Mechanics Publisher: Academic press, Inc.

• Deformation of a deformable body can be discontinuous (localized on faults) or continuous. • Strain: change of size and shape of a body

Basics of continuum mechanics, Strain A. Displacements, trajectories, streamlines, emission lines 1 - Lagrangian parametrisation 2 -Eulerian parametrisation B Homogeneous and tangent Homogeneous transformation 1 - Definition of an homogeneous transformation 2 - Convective transport equation during homogeneous transformation 3 -Tangent homogeneous transformation C Strain during homogeneous transformation 1 -The Green strain tensor and the Green deformation tensor Infinitesimal vs finite deformation 2 - Polar factorisation D Properties of homogeneous transformations 1 - Deformation of line 2 - Deformation of spheres 3 - The strain ellipse 4 - The Mohr circle E Infinitesimal deformation 1 - Definition 2 - The infinitesimal strain tensor 3 -Polar factorisation 4 - The Mohr circle F Progressive, finite, and infinitesimal deformation : 1 - Rotational/non rotational deformation 2 - Coaxial Deformation G Case examples 1 - Uniaxial strain 2 - Pure shear, 3 - Simple shear 4 - Uniform dilatational strain

A. Describing the transformation of a body • Reference frame (coordinate system): R • Reference state of the medium (initial configuration): • State of the medium at time t: – Position (at t), particle path – displacement (t 0 and t), – Velocity (at time t) – Strain (changes in length of lines, angles between lines, volume) k 0 kt

A. 1 Lagrangian parametrisation • Displacements • Trajectories • Streamlines

A. 1 Lagrangian parametrisation • Volume Change

A. 2 Eulerian parametrisation • Trajectories: • Streamlines: (at time t)

A. 3 Stationary Velocity Field • Velocity is independent of time NB: If the motion is stationary in the chosen reference frame then trajectories=streamlines

B. Homogeneous Tansformation • definition

Homogeneous Transformation • Changing reference frame

Homogeneous Transformation • Convective transport of a vector Implication: Straight lines remain straight during deformation

Homogeneous transformation • Convective transport of a volume

Homogeneous transformation • Convective transport of a surface

Tangent Homogeneous Deformation • Any transformation can be approximated locally by its tangent homogeneous transformation

Tangent Homogeneous Deformation • Any transformation can be approximated locally by its tangent homogeneous transformation

Tangent Homogeneous Deformation • Displacement field

D. Strain during homogeneous Deformation • The Cauchy strain tensor (or expansion tensor)

Strain during homogeneous Deformation • Stretch (or elongation) in the direction of a vector

Strain during homogeneous Deformation • Stretch (or elongation) in the direction of a vector • Extension (or extension ratio), relative length change

Strain during homogeneous Deformation • Change of angle between 2 initially orthogonal vectors • Shear angle

Strain during homogeneous Deformation • Signification of the strain tensor components

Strain during homogeneous Deformation An orthometric reference frame can be found in which the strain tensor is diagonal. This define the 3 principal axes of the strain tensor.

Strain during homogeneous Deformation • The Green-Lagrange strain tensor (strain tensor)

Strain during homogeneous Deformation • The Green-Lagrange strain tensor

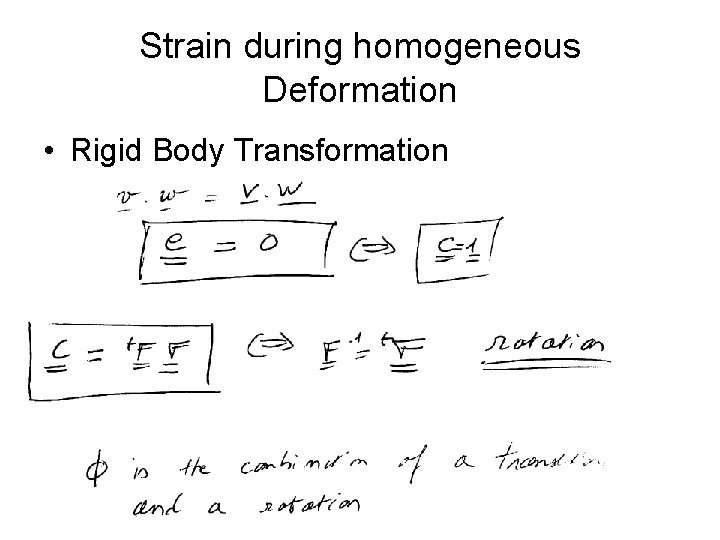
Strain during homogeneous Deformation • Rigid Body Transformation

Strain during homogeneous Deformation • Rigid Body Transformation

Strain during homogeneous Deformation • Polar factorisation

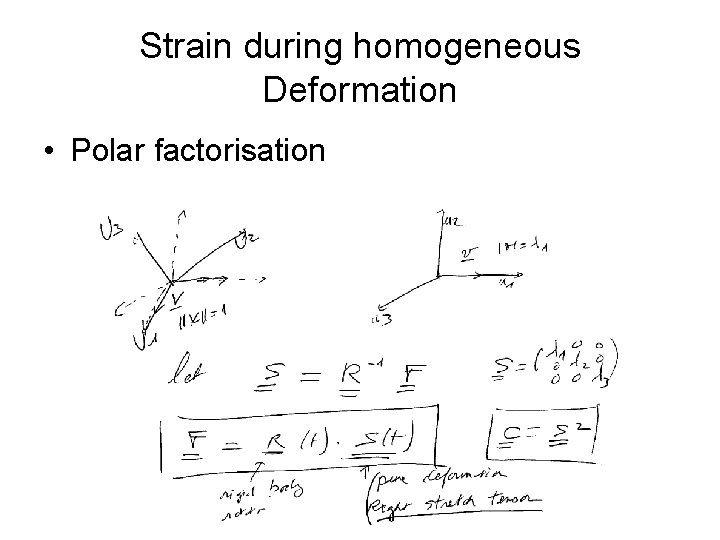
Strain during homogeneous Deformation • Polar factorisation

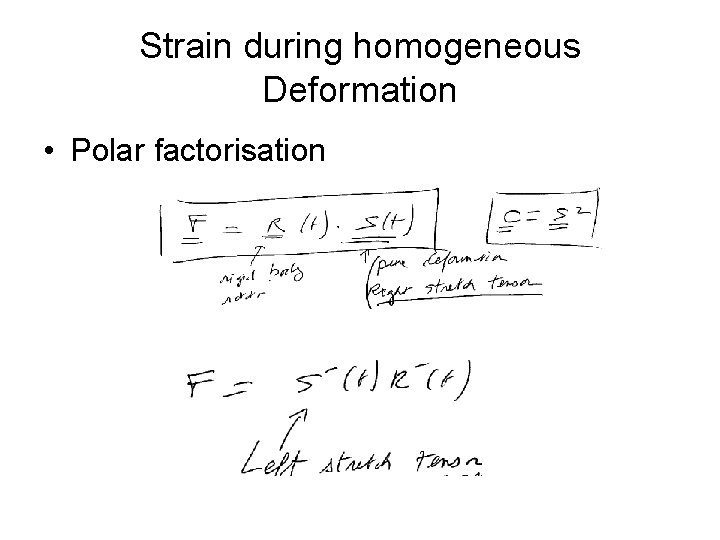
Strain during homogeneous Deformation • Polar factorisation

Strain during homogeneous Deformation • Pure deformation: The principal strain axes remain parallel to themselves during deformation

D. Some properties of homogeneous Deformation

Some properties of homogeneous Deformation • The strain tensor is uniquely characterized by the strain ellipsoid (a sphere with unit radius in the initial configuration)

Some properties of homogeneous Deformation • The strain tensor is uniquely characterized by the strain ellipsoid (a sphere with unit radius in the initial configuration)

Some properties of homogeneous Deformation • The Mohr Circle for finite strain

Some properties of homogeneous Deformation • The Mohr Circle for finite strain

Some properties of homogeneous Deformation • Note that knowing the strain tensor associated to an homogeneous transformation does not define the uniquely the transformation (the translation and the rotation terms remain undetermined)

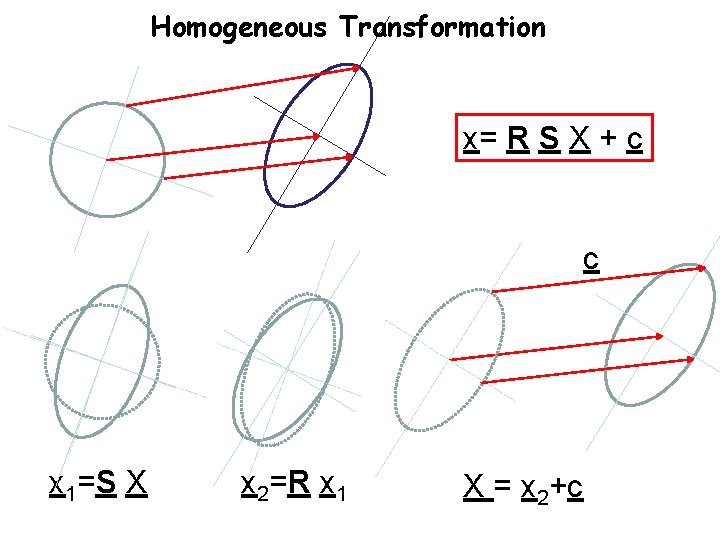
Homogeneous Transformation x= R S X + c c x 1=S X x 2=R x 1 X = x 2+c

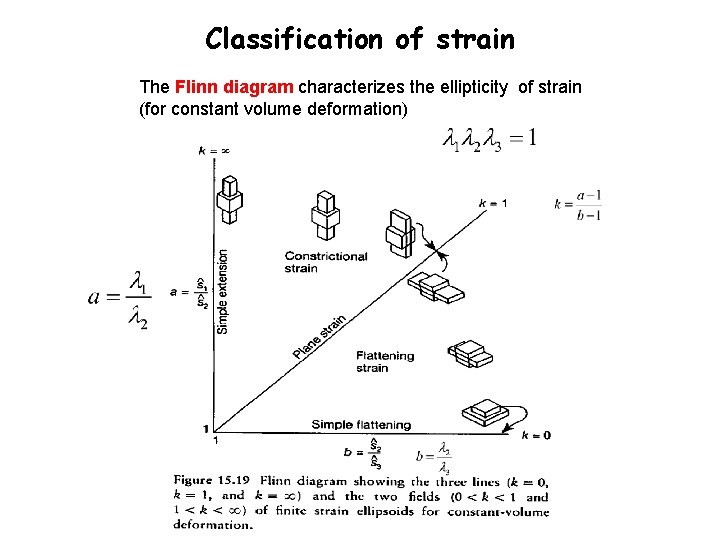
Classification of strain The Flinn diagram characterizes the ellipticity of strain (for constant volume deformation)

E. Infinitesimal transformation Infinitesimal strain tensor

Infinitesimal transformation Infinitesimal strain tensor

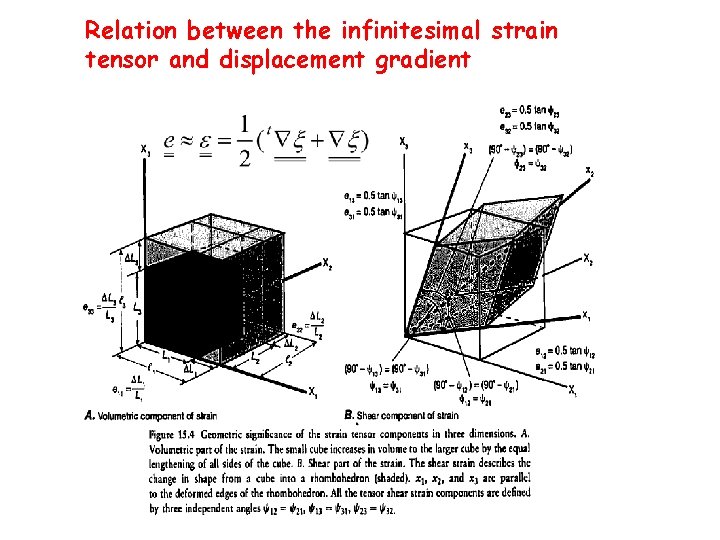
Relation between the infinitesimal strain tensor and displacement gradient

The strain ellipse NB: The representation of principal extensions on this diagram is correct only for infinitesimal strain only

Rk: For an infinitesimal deformation the principal extensions are small (typically less than 1%). The strain ellipse are close to a circle. For visualisation the strain ellipse is represented with some exaggeration

F. Progressive, finite and infinitesimal deformation – Finite deformation is said to be non-rotational if the principle strain axis in the initial and final configurations are parallel. This characterizes only how the final state relates to the initial state – Finite deformation of a body is the result of a deformation path (progressive deformation). – There is an infinity of possible deformation paths to reach a particular finite strain. – Generally infinitesimal strain (or equivalently the strain rate tensor) is used to describe incremental deformation of a body that has experienced some finite strain – A progressive deformation is said to be coaxial if the principal axis of the infinitesimal strain tensor remain parallel to the principal axis of the finite strain tensor. This characterizes the deformation path.

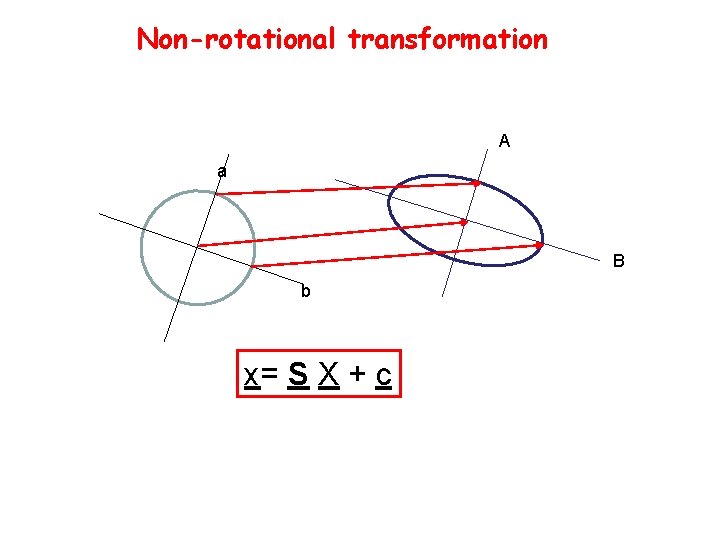
Non-rotational transformation A a B b x= S X + c

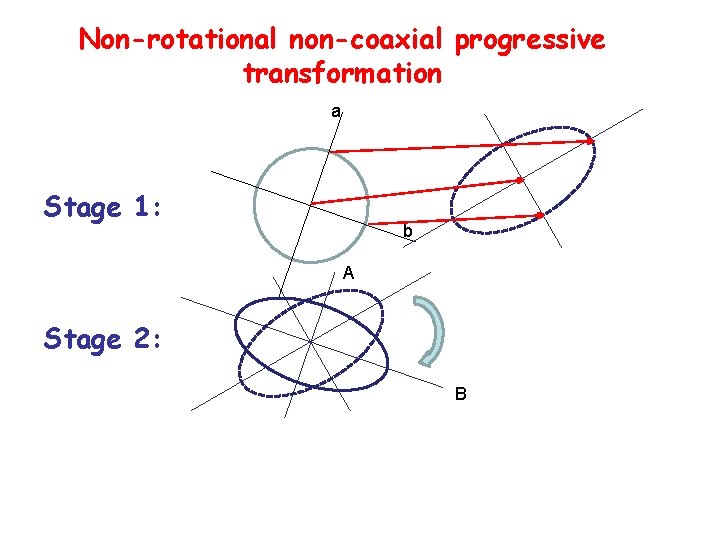
Non-rotational non-coaxial progressive transformation a Stage 1: b A Stage 2: B

Rotational vs non-rotational deformation If A and B are parallel to a and b respectively the deformation is said to be non-rotational (This means R= 1)

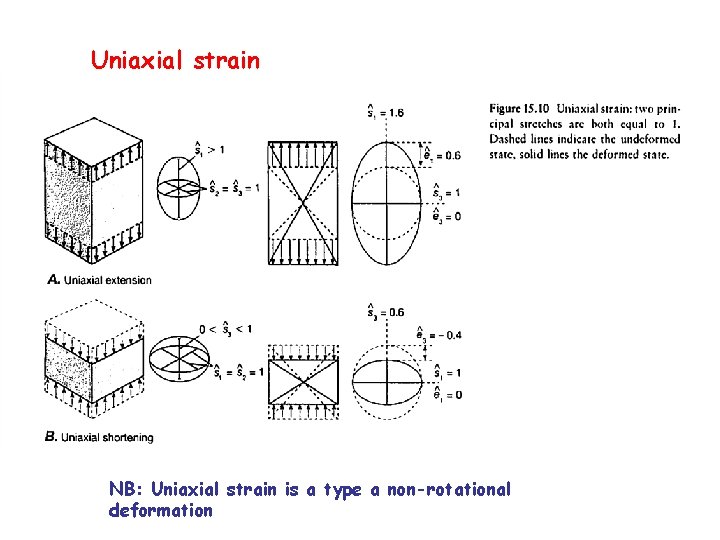
Uniaxial strain NB: Uniaxial strain is a type a non-rotational deformation

Pure Shear NB: Pure shear in is a type a non-rotational deformation

Simple Shear NB: Simple shear is rotational

Progressive pure shear is a type of coaxial strain

Progressive simple Shear Progressive simple shear is non coaxial