II Linear Block Codes Digital Communication Systems Source
II. Linear Block Codes
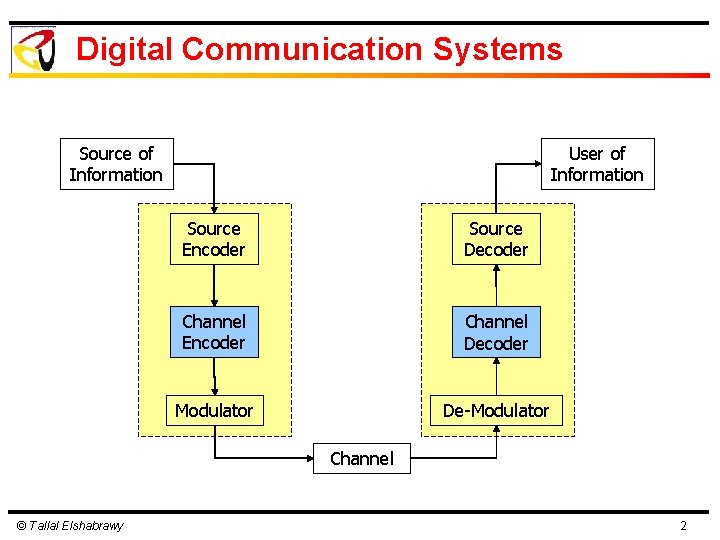
Digital Communication Systems Source of Information User of Information Source Encoder Source Decoder Channel Encoder Channel Decoder Modulator De-Modulator Channel © Tallal Elshabrawy 2
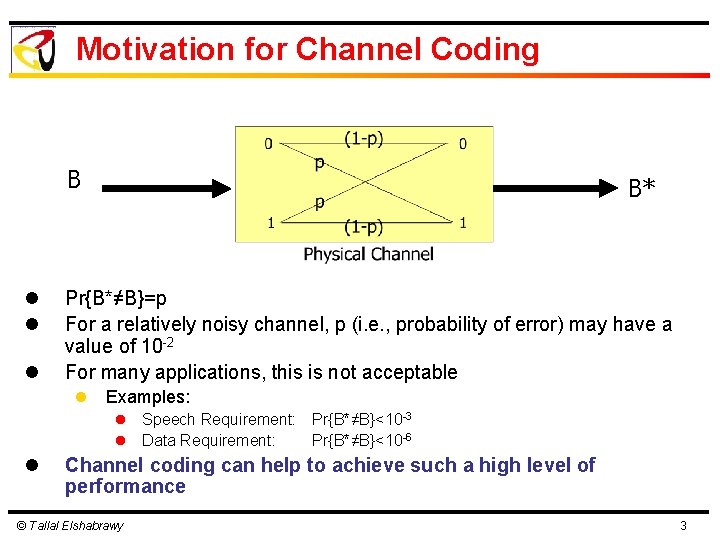
Motivation for Channel Coding B l l l B* Pr{B*≠B}=p For a relatively noisy channel, p (i. e. , probability of error) may have a value of 10 -2 For many applications, this is not acceptable l Examples: l Speech Requirement: Pr{B*≠B}<10 -3 l Data Requirement: Pr{B*≠B}<10 -6 l Channel coding can help to achieve such a high level of performance © Tallal Elshabrawy 3
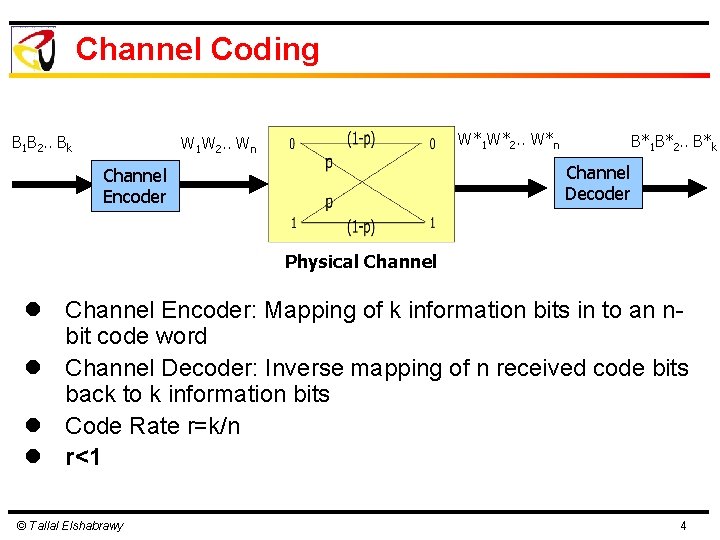
Channel Coding B 1 B 2. . Bk W*1 W*2. . W*n W 1 W 2. . Wn B*1 B*2. . B*k Channel Decoder Channel Encoder Physical Channel Encoder: Mapping of k information bits in to an nbit code word l Channel Decoder: Inverse mapping of n received code bits back to k information bits l Code Rate r=k/n l r<1 © Tallal Elshabrawy 4
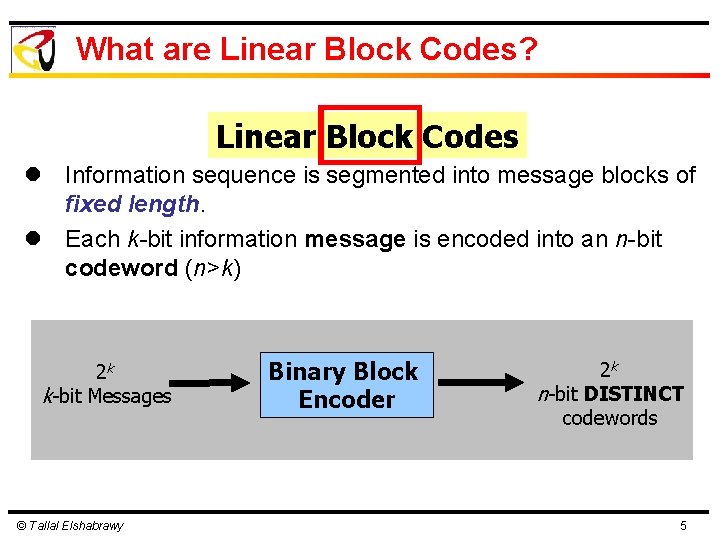
What are Linear Block Codes? Linear Block Codes l Information sequence is segmented into message blocks of fixed length. l Each k-bit information message is encoded into an n-bit codeword (n>k) 2 k k-bit Messages © Tallal Elshabrawy Binary Block Encoder 2 k n-bit DISTINCT codewords 5

What are Linear Block Codes? Linear Block Codes l Modulo-2 sum of any two codewords is ……… also a codeword l Each codeword v that belongs to a block code C is a linear combination of k linearly independent codewords in C, i. e. , © Tallal Elshabrawy 6

Linear Independence l A set of vectors g 0, g 1, …, gk-1 are linearly independent if there exists no scalars u 0, u 1, …, uk-1 that satisfy Unless u 0=u 1=…= uk-1=0 l Examples l [0 1 0 ], [1 0 1], [1 1 1] are ……… l Linearly Dependent l [0 1 0 ], [1 0 1], [0 0 1] are ……… l Linearly Independent © Tallal Elshabrawy 7

Why Linear? l Encoding Process l Store and Index 2 k codewords of length n l Complexity l Huge storage requirements for large k l Extensive search processing for large k l Linear Block Codes l Stores k linearly independent codewords l Encoding process through linear combination of codewords g 0, g 1, …, gk-1 based on input message u=[u 0, u 1, …, uk-1] Generator Matrix © Tallal Elshabrawy 8
![Example u= [0 1 1 0] Linear Block Encoder (v=u. G) v= g 1+g Example u= [0 1 1 0] Linear Block Encoder (v=u. G) v= g 1+g](http://slidetodoc.com/presentation_image_h/ab18a30b7de43ae17bc8fecb20e1f8ee/image-9.jpg)
Example u= [0 1 1 0] Linear Block Encoder (v=u. G) v= g 1+g 2 v= [1 0 0 0 1 1 0] © Tallal Elshabrawy Message Codeword 0000000 0001 1010001 g 3 0010 1110010 g 2 0011 0100 0110100 0101 1100101 0110 1000110 0111 0010111 1000 1101000 1001 0111001 1010 0011010 1011 1001011 1100 1011100 1101 0001101 1110 0101110 1111111 g 0 9
![Example Linearly Dependent u= [0 1 1 1] u= [1 0 0 1] Block Example Linearly Dependent u= [0 1 1 1] u= [1 0 0 1] Block](http://slidetodoc.com/presentation_image_h/ab18a30b7de43ae17bc8fecb20e1f8ee/image-10.jpg)
Example Linearly Dependent u= [0 1 1 1] u= [1 0 0 1] Block Encoder (v=u. G) v= g 1+g 2+g 3 v= [0 1 1 1 0 0 1] © Tallal Elshabrawy NOT DISTINCT v= g 0+g 3 v= [0 1 1 1 0 0 1] 10
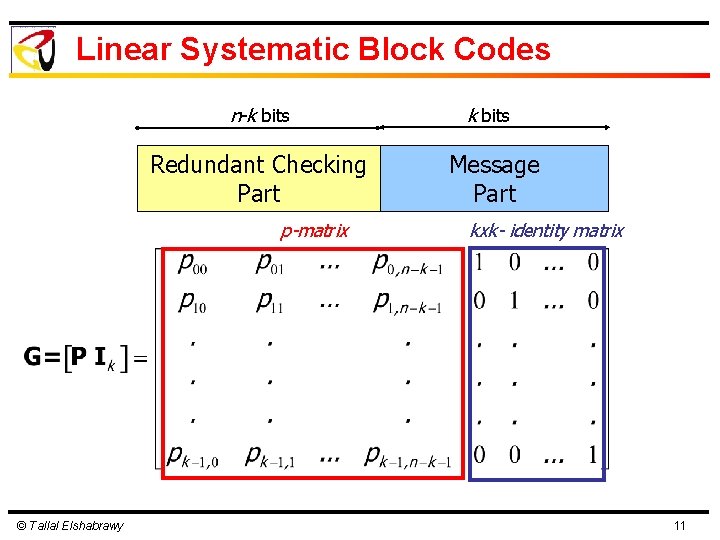
Linear Systematic Block Codes n-k bits Redundant Checking Part Message Part p-matrix © Tallal Elshabrawy kxk- identity matrix 11

The Parity Check Matrix l For any k x n matrix G with k linearly independent rows, there exists an (n-k) x n matrix H (Parity Check Matrix), such that l G. HT=0 © Tallal Elshabrawy 12
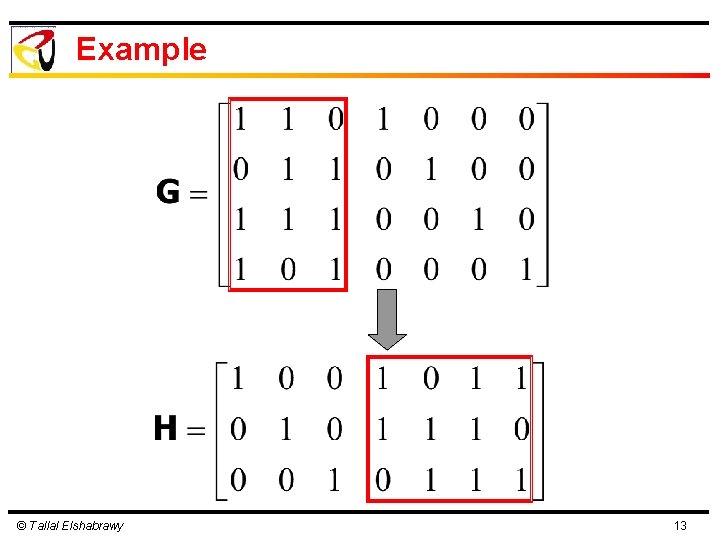
Example © Tallal Elshabrawy 13
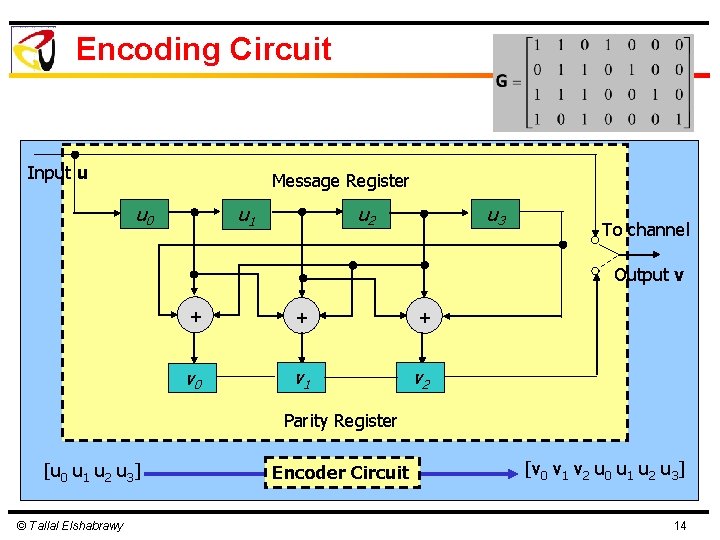
Encoding Circuit Input u Message Register u 0 u 3 u 2 u 1 To channel Output v + + + v 0 v 1 v 2 Parity Register [u 0 u 1 u 2 u 3] © Tallal Elshabrawy Encoder Circuit [v 0 v 1 v 2 u 0 u 1 u 2 u 3] 14
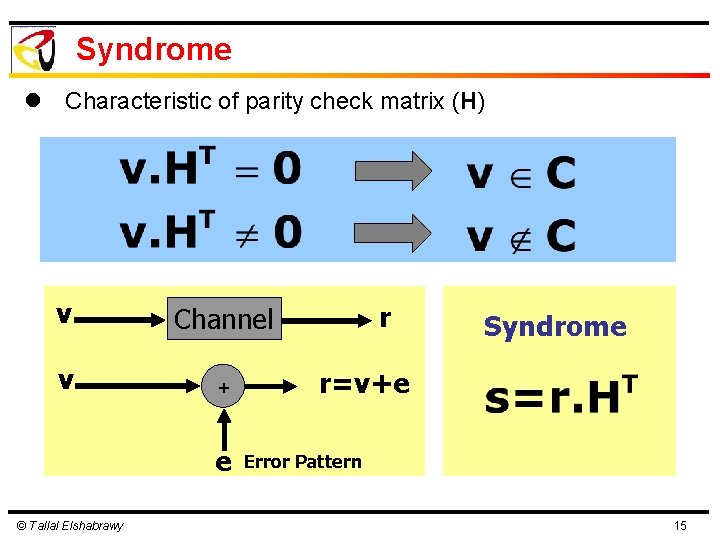
Syndrome l Characteristic of parity check matrix (H) v Channel v + e © Tallal Elshabrawy r Syndrome r=v+e Error Pattern 15

Error Detection r is NOT a codeword An Error is Detected: What Options do we have? l Ask for Retransmission of Block l Automatic Repeat Request (ARQ) l Attempt the Correction of Block l Forward Error Correction © Tallal Elshabrawy 16
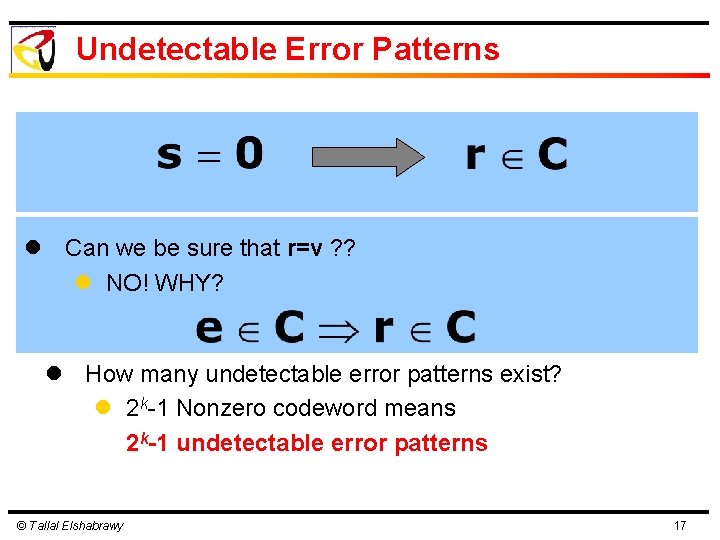
Undetectable Error Patterns l Can we be sure that r=v ? ? l NO! WHY? l How many undetectable error patterns exist? l 2 k-1 Nonzero codeword means 2 k-1 undetectable error patterns © Tallal Elshabrawy 17
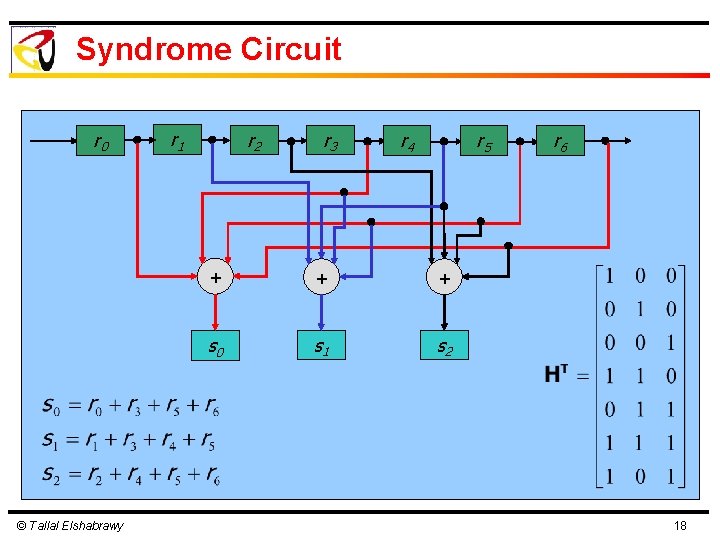
Syndrome Circuit r 0 © Tallal Elshabrawy r 1 r 2 r 3 r 4 r 5 + + + s 0 s 1 s 2 r 6 18
- Slides: 18