II 6 Introduction on unbounded linear operators Theorem

II. 6 Introduction on unbounded linear operators

Theorem 3. 3 Riesz Representation Theorem Let X be a Hilbert space and then there is Furthermore the map is conjugate linear and such that


Unbounded linear operator p. 1 E, F: Banach spaces Any linear operator A defined on with range in F is called unbounded linear operator from E to F

Unbounded linear operator p. 2 D(A): domain of A A is called bounded if there is such that
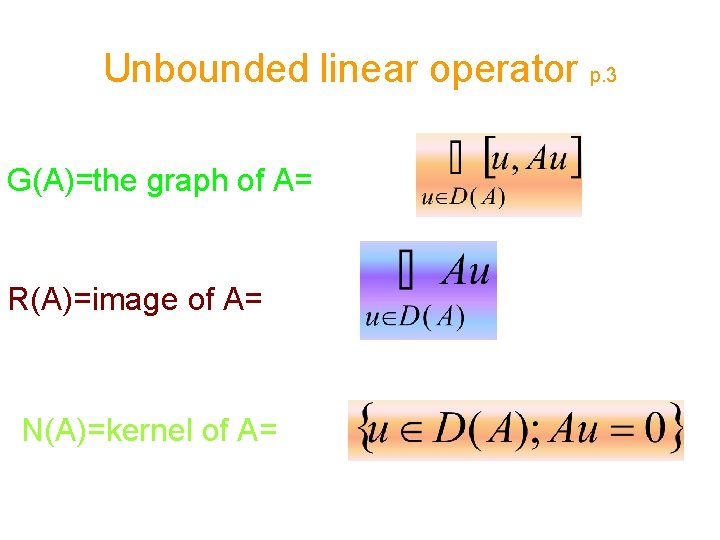
Unbounded linear operator p. 3 G(A)=the graph of A= R(A)=image of A= N(A)=kernel of A=

Unbounded linear operator p. 4 A is called closed if G(A) is closed in i. e. if then

Remark If A is closed, then N(A) is closed in E. In most application, D(A)is dense in E.

Definition of Adjoint A* of A Suppose A is an unbounded linear operator from a Banach space E to a Banach space F with D(A) dense in E Define the adjoint A* of A from F´ to E´ as follows: p. 1

Definition of Adjoint A* of A p. 2 For let By Hahn-Banach Thm, g can be extended to an element of E´. Since D(A) is dense in E, the extension is unique and is denoted by A*v

Definition of Adjoint A* of A p. 3 Obviously, A* is characterized by is linear

Remark If E = F=H is a Hilbert space Identify H´and H by Riesz Representation as a fun. of u is bounded linear on D(A)

Example In If then

Proposition II. 16 Let A: D(A) → F be an unbounded linear operator with dense domain. Then A* is closed i. e. G(A*) is closed in

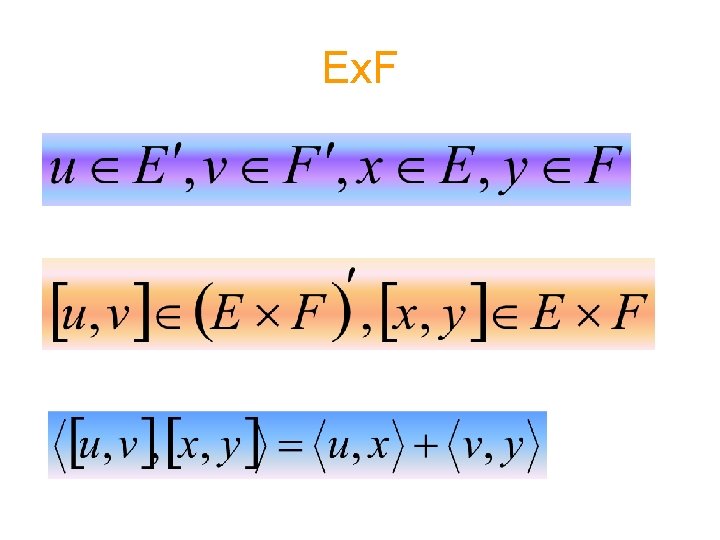
Ex. F
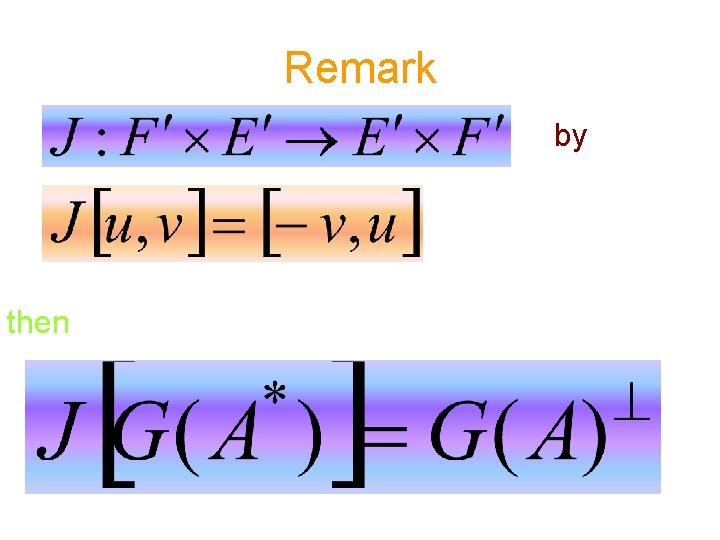
Remark by then


Remark (26) (27) (28) (29)
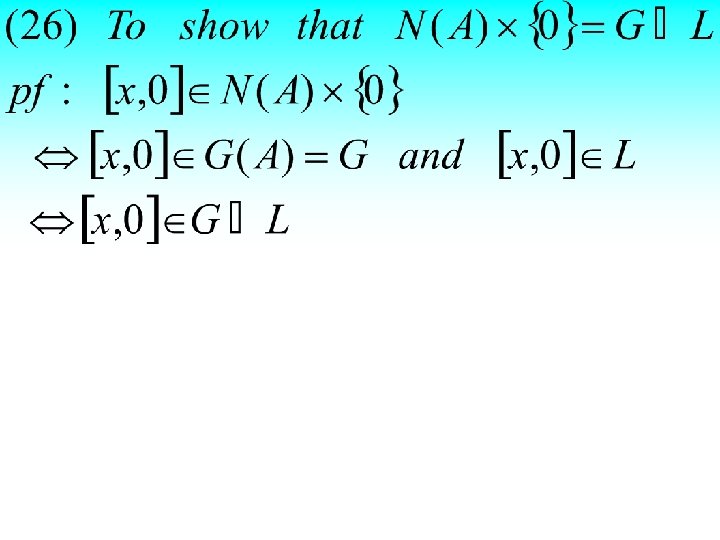




Corollary II. 17 be an unbounded Let closed linear operator with then (i) (iii) (iv)




II. 7 Characterization of operators with closed range Surjective operators Bounded operators

Theorem II. 18 be an unbounded Let closed linear operator with then the following properties are equivalent (i) R(A) is closed (ii) R(A*) is closed (iii) (iv)


Theorem II. 19 Let be an unbounded closed linear operator with then the following properties are equivalent (a) A is surjective i. e. R(A)=F (b ) (c)




Theorem II. 19 be an unbounded Let closed linear operator with then (i) (iii) (iv)

Theorem I. 11 Suppose and are convex and suppose that there is such that and is continuous at

- Slides: 37