IGCSE Further MathsC 1 Differentiation Dr J Frost

IGCSE Further Maths/C 1 Differentiation Dr J Frost (jfrost@tiffin. kingston. sch. uk) www. drfrostmaths. com Objectives: Last modified: 3 rd January 2016

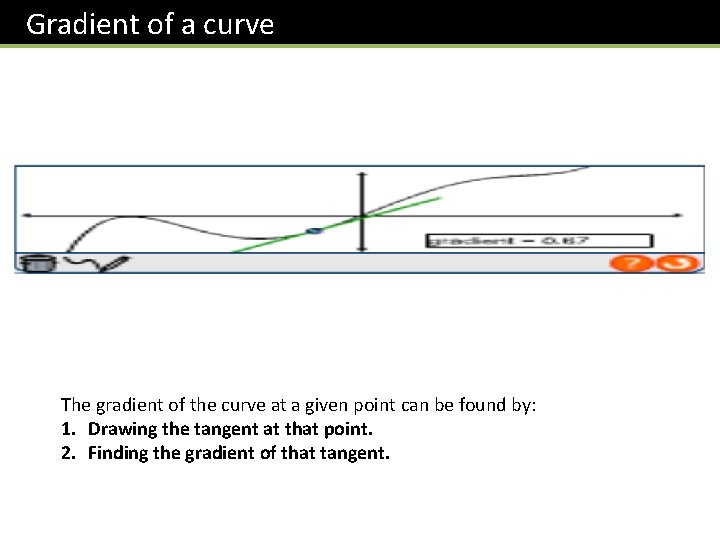
Gradient of a curve The gradient of the curve at a given point can be found by: 1. Drawing the tangent at that point. 2. Finding the gradient of that tangent.

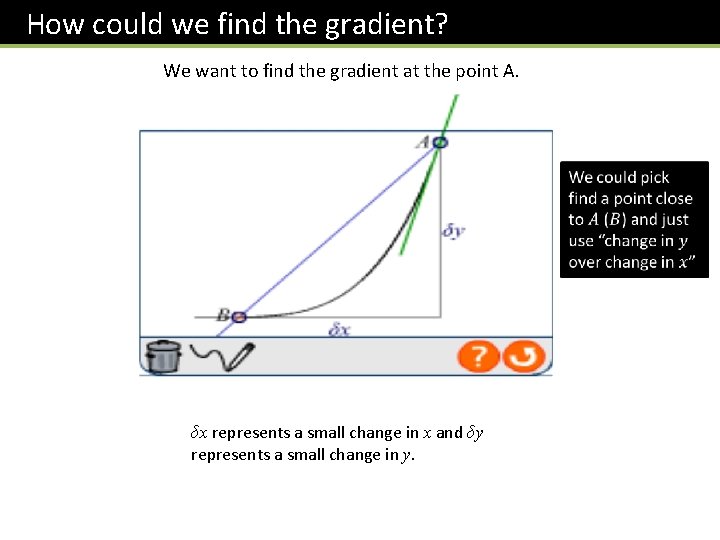
How could we find the gradient? We want to find the gradient at the point A. δx represents a small change in x and δy represents a small change in y.

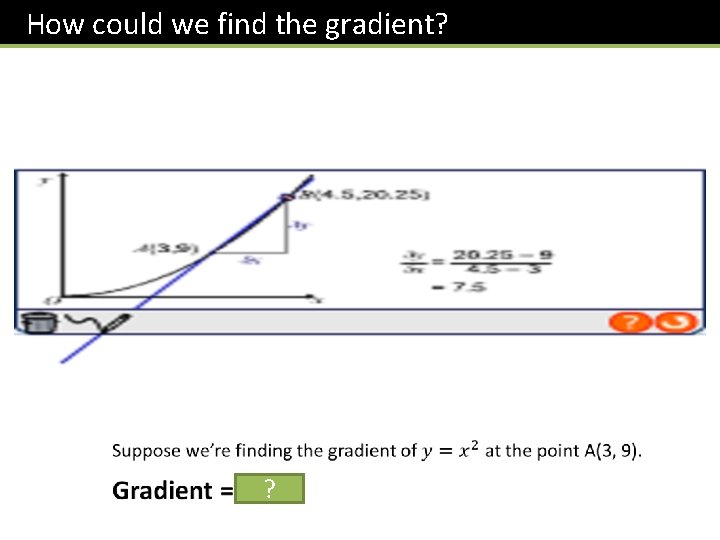
How could we find the gradient? ?

How could we find the gradient? Point (1, 1) (4, 16) (2. 5, 6. 25) (10, 100) Gradient 2 8 5 20 ? Let’s prove it. . .

Proof that ‘gradient function’ of y = x 2 is 2 x Suppose we add some tiny value, h, to x. Then: The “lim” bit means “what this expression approaches as h tends towards 0” (x + h, (x+h) ? 2) (x, x? 2) δy δx ? The h disappears as h tends towards 0. Note: This proof will not be examined.

Terminology Original function Gradient function

Can you spot the pattern? ? ?

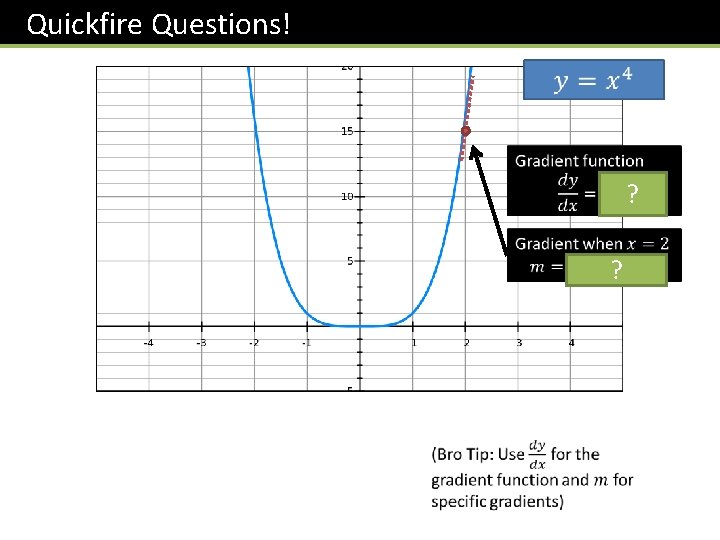
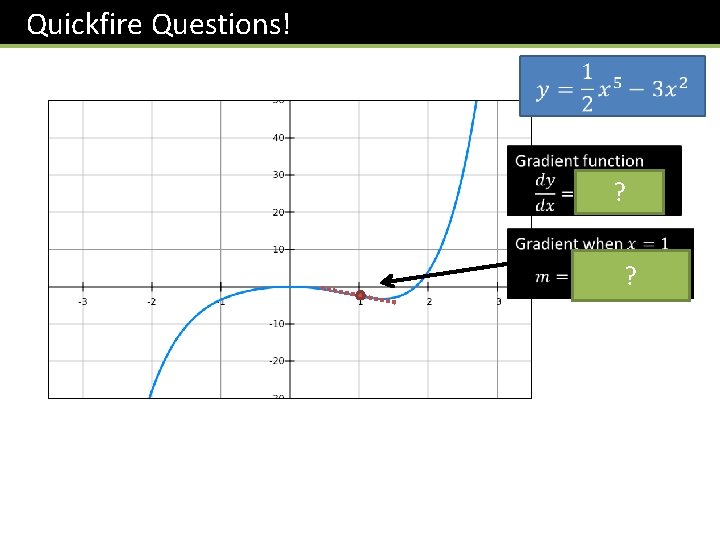
Quickfire Questions! ? ?

Quickfire Questions! ? ?

Quickfire Questions! ? ?

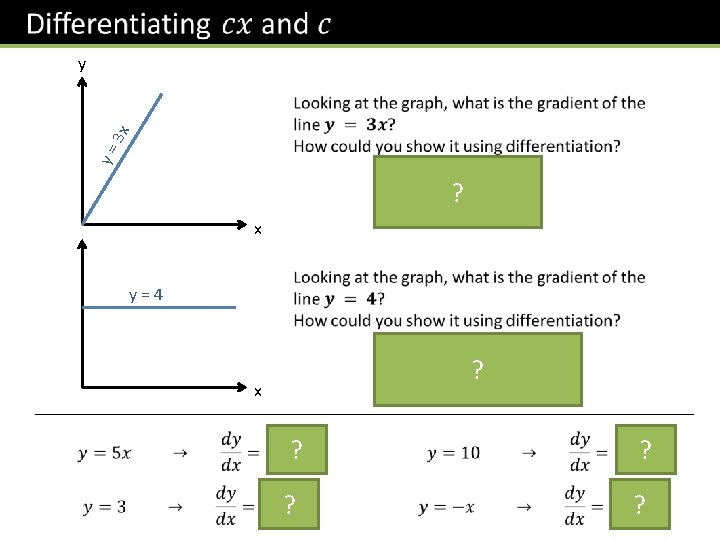
y= 3 x y ? x y=4 ? x ? ?

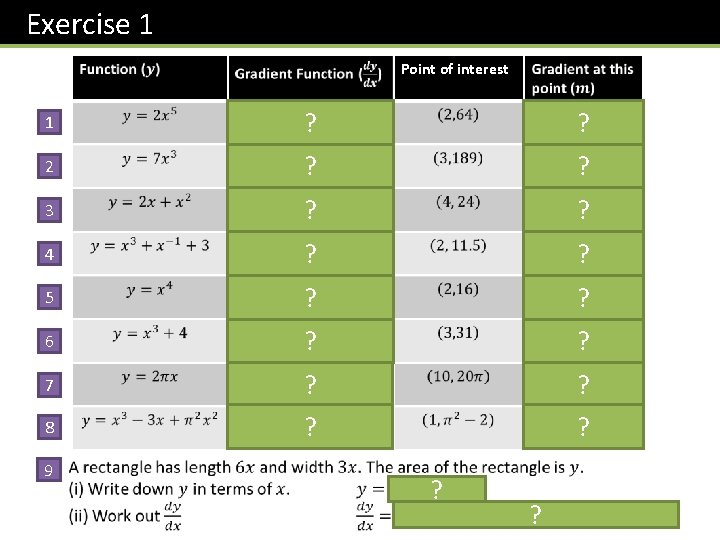
Exercise 1 Point of interest 1 ? ? 2 ? ? 3 ? ? 4 ? ? 5 ? ? 6 ? ? 7 ? ? 8 9 ? ?

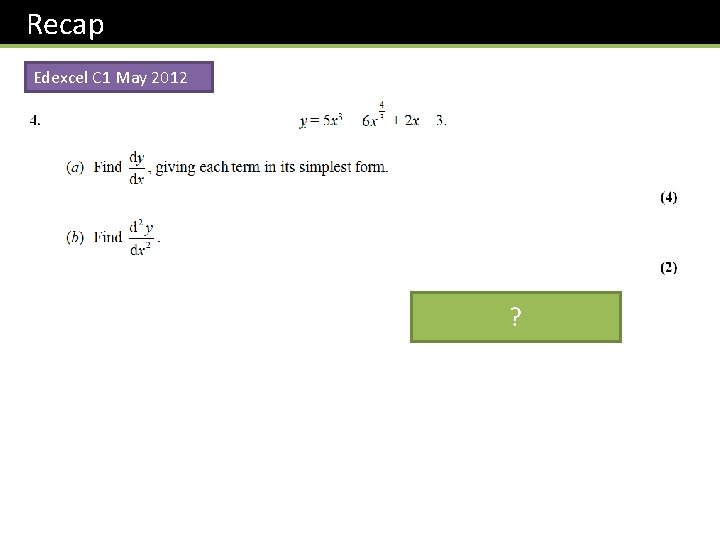
Recap Edexcel C 1 May 2012 ?

Turning more complex expressions into polynomials ? ? ?

C 1 Exercise 7 E (Page 115) 1 ? ? ? ? ? 2 ? ?

Further Practice 5 1 ? 2 ? ? 3 ? ? ? 4 6 ? ?

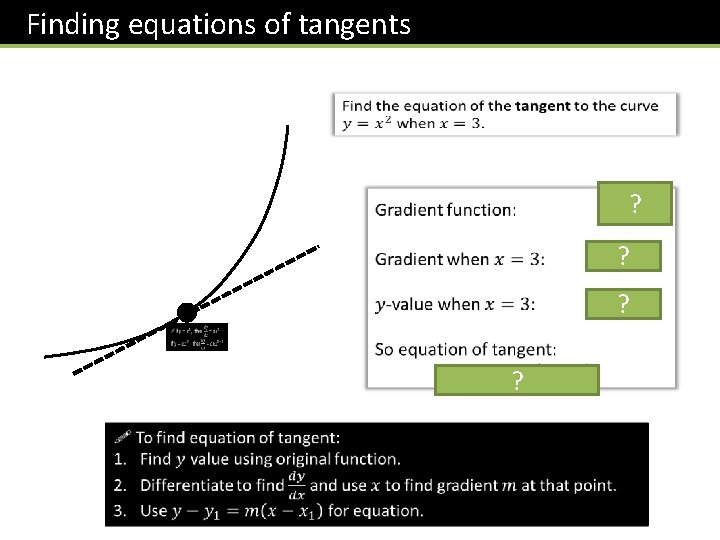
Finding equations of tangents ? ?

Finding equations of tangents ?

Test Your Understanding June 2012 Paper 1 (Q 1 on provided sheet) ? ?

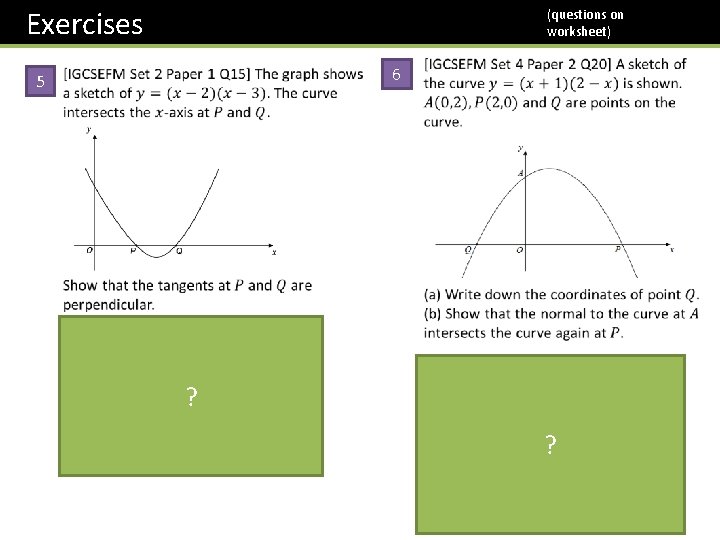
Exercises (questions on worksheet) 3 1 ? ? 4 ? 2 ? ? ?

Exercises (questions on worksheet) 6 5 ? ?

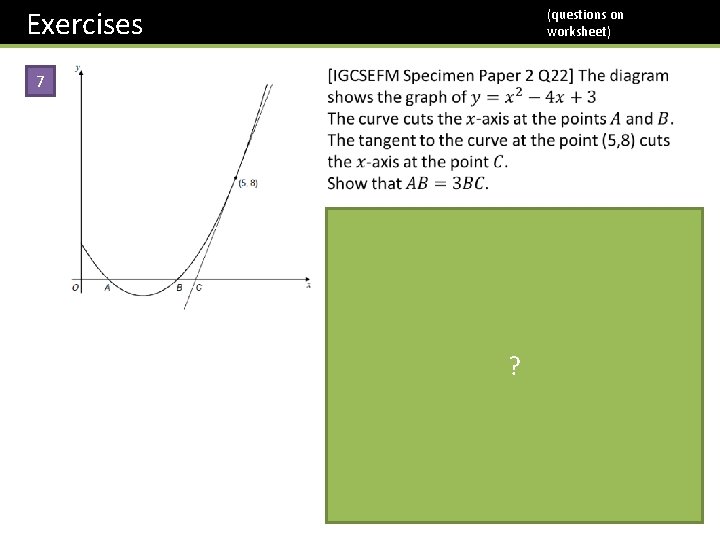
Exercises (questions on worksheet) 7 ?

Exercises (questions on worksheet) Edexcel C 1 Jan 2013 ? ? (9, -1) ?

Exercises ? ? ?

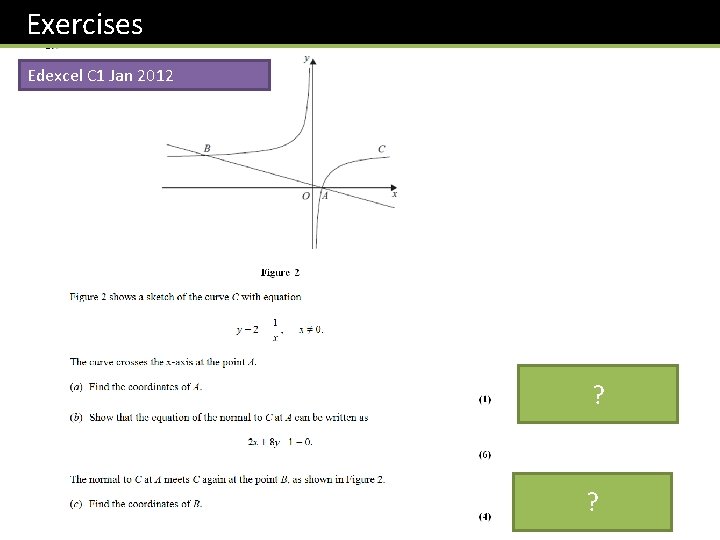
Exercises Edexcel C 1 Jan 2012 ? ?

Exercises Edexcel C 1 Jan 2011 ? ? ?

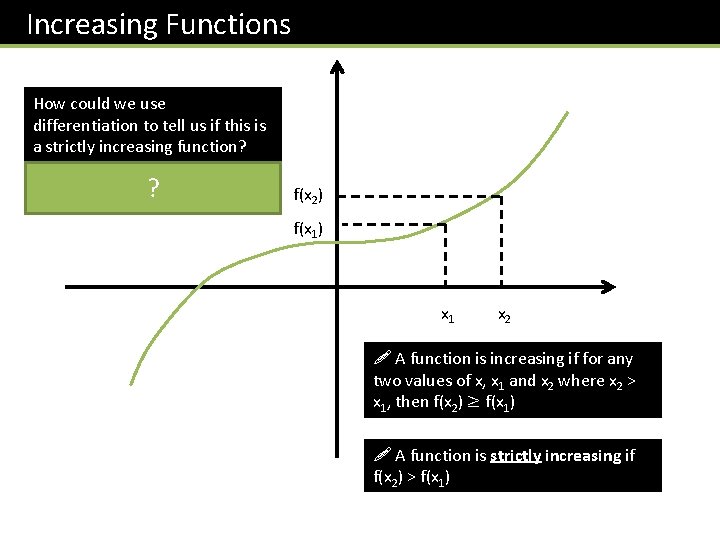
Increasing Functions How could we use differentiation to tell us if this is a strictly increasing function? . . . if the gradient is always positive, i. e. f’(x)? > 0 for all x. f(x 2) f(x 1) x 1 x 2 ! A function is increasing if for any two values of x, x 1 and x 2 where x 2 > x 1, then f(x 2) ≥ f(x 1) ! A function is strictly increasing if f(x 2) > f(x 1)

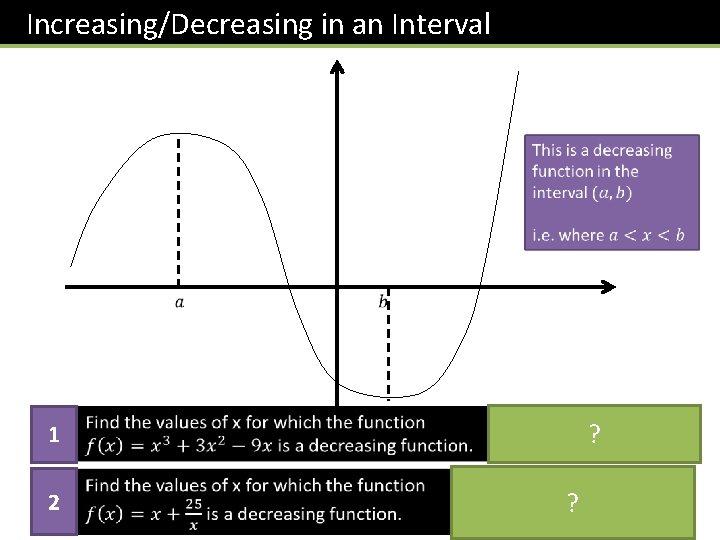
Increasing/Decreasing in an Interval 1 2 3 x 2 + 6 x – 9 < 0 Thus -3 < x ? <1 ?

Example Questions a? b? ! To show that a function is ALWAYS increasing, complete the square to show the minimum value of expression is positive.

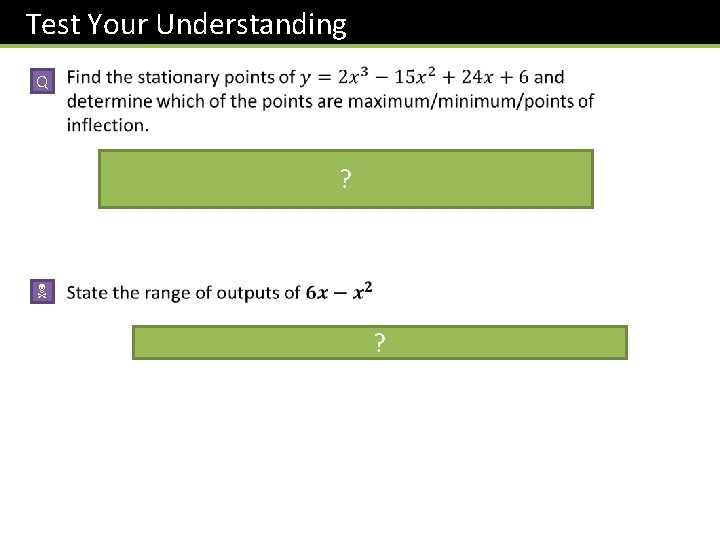
Test Your Understanding ? ?

Exercises 1 3 ? ? ? ? 4 2 ? ? ? ? 5

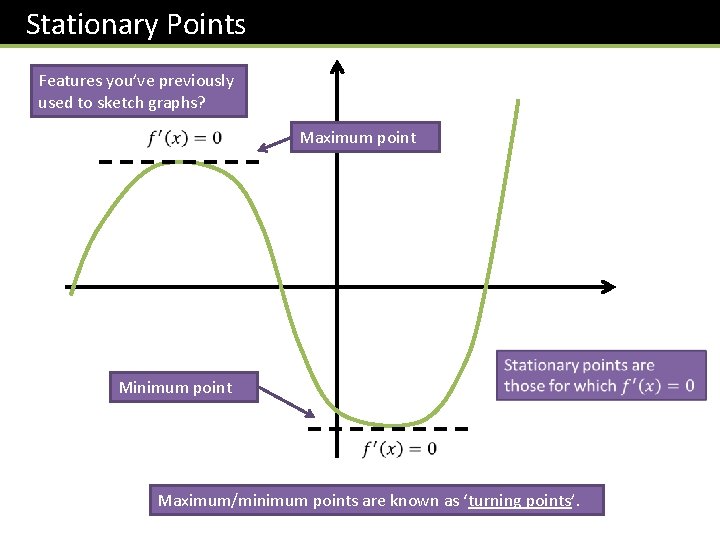
Stationary Points Features you’ve previously used to sketch graphs? Maximum point Minimum point Maximum/minimum points are known as ‘turning points’.

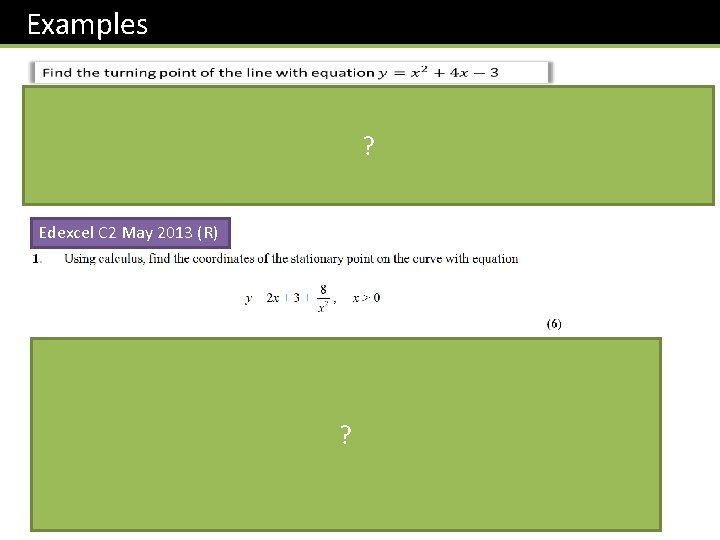
Examples ? Edexcel C 2 May 2013 (R) ?

Test Your Understanding ? ?

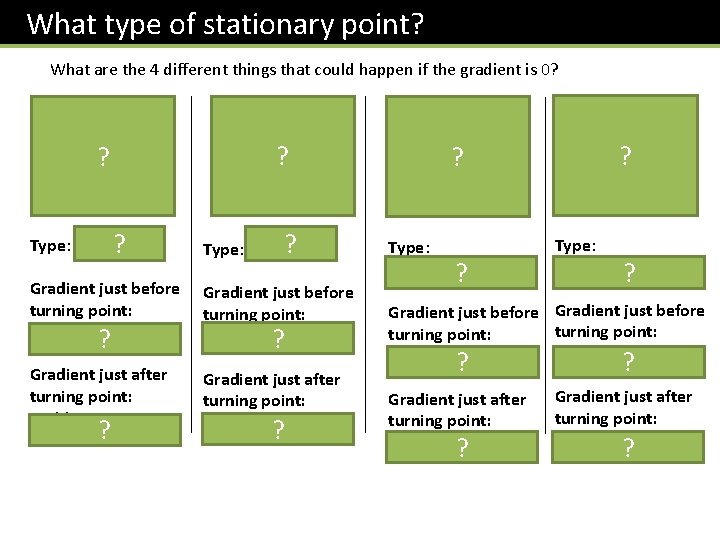
What type of stationary point? What are the 4 different things that could happen if the gradient is 0? ? ? Type: minimum ? ? Type: maximum Gradient just before turning point: Negative Gradient just before turning point: Positive ? ? Gradient just after turning point: Positive ? Gradient just after turning point: Negative ? ? ? Type: ‘point of inflection’ ? Gradient just before turning point: Negative Positive ? ? Gradient just after turning point: Positive ? Gradient just after turning point: Negative ?

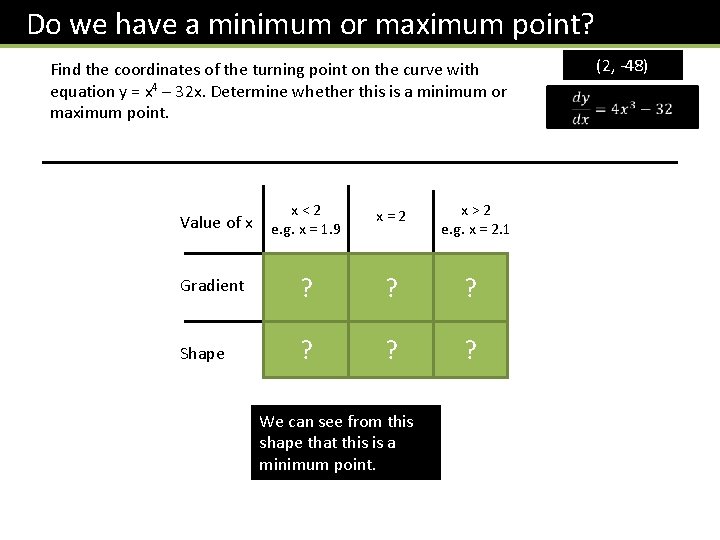
Do we have a minimum or maximum point? Find the coordinates of the turning point on the curve with equation y = x 4 – 32 x. Determine whether this is a minimum or maximum point. Value of x x<2 e. g. x = 1. 9 x=2 x>2 e. g. x = 2. 1 Gradient e. g. -4. 56 ? ? 0 e. g. 5. 04 ? ? Shape We can see from this shape that this is a minimum point. ? ? (2, -48)

Another example Set 3 Paper 1 Q 16 ? Hence find stationary point ? Determine type of point Grad before At stationary point Grad after

Test Your Understanding Q (1, 17) is a maximum point. (4, -10) is a maximum point. ? N ?

Exercises 1 ? ? ? 2 ?