IFT 615 Intelligence Artificielle JeanFranois Landry Dpartement dinformatique




























- Slides: 52

IFT 615 Intelligence Artificielle Jean-François Landry Département d’informatique Université de Sherbrooke Réseaux bayésiens http: //planiart. usherbrooke. ca/~jflandry/ift 615/

Sujets couverts l C’est quoi un réseau bayésien (RB) ? u Structure d’un RB u Signification l Indépendance conditionnelle dans un RB. l Inférence dans un réseau bayésien u Inférence exacte u Inférence approximative l Diagrammes d’influence IFT 615 2

Réseaux bayésiens l Les RB sont un mariage entre la théorie des graphes et la théorie des probabilités. l Un RB représente les connaissances probabilistes à partir d’une situation donnée : u Par exemple, les connaissances cliniques d’un médecin sur des liens de causalité entre maladies et symptômes. l Les RB sont utiles pour modéliser des connaissances d’un système expert ou d’un système de support à la décision, dans une situation pour laquelle : u La causalité joue un rôle important : des événements causent d’autres. u Notre compréhension de la causalité des événements est incomplète : on doit recourir aux probabilités. IFT 615 3

Syntaxe l Un RB est un graphe u orienté, u acyclique, u dont les nœuds sont des variables (le plus souvent aléatoires) et u les arcs représentent » des dépendances (causalités) probabilistes entre les variables et » des distributions de probabilités conditionnelles (locales) pour chaque variable étant donné ses parents. IFT 615 4

Exemple l Considérons la situation suivante : u Je suis au travail. Mes voisins Marie et Jean m’ont promis de m’appeler chaque fois que mon alarme sonne. u Mon voisin Jean m’appelle pour me dire que mon alarme sonne. » Parfois il confond l’alarme avec la sonnerie du téléphone. u Par contre ma voisine Marie ne m’appelle pas. » Parfois elle met la musique trop fort. u Parfois mon alarme se met à sonner lorsqu’il y a de légers séismes. u Comment conclure qu’il y a un cambriolage chez moi ? l On peut représenter cette situation par un RB. IFT 615 5

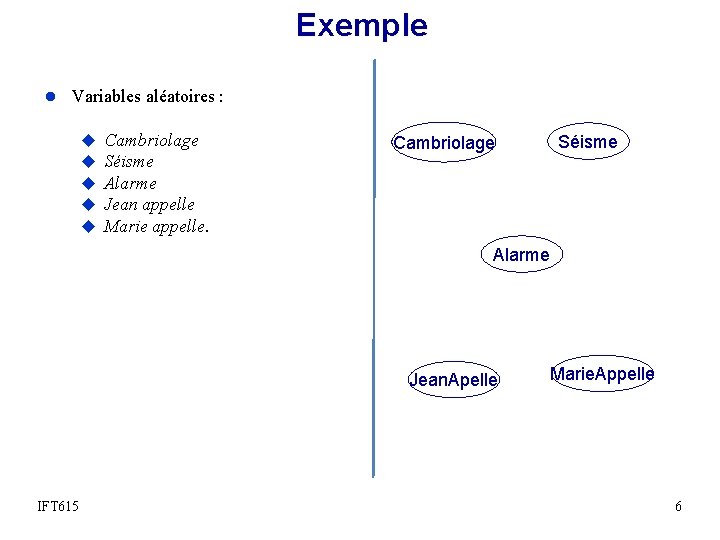
Exemple l Variables aléatoires : u u u Cambriolage Séisme Alarme Jean appelle Marie appelle. Séisme Cambriolage Alarme Jean. Apelle IFT 615 Marie. Appelle 6

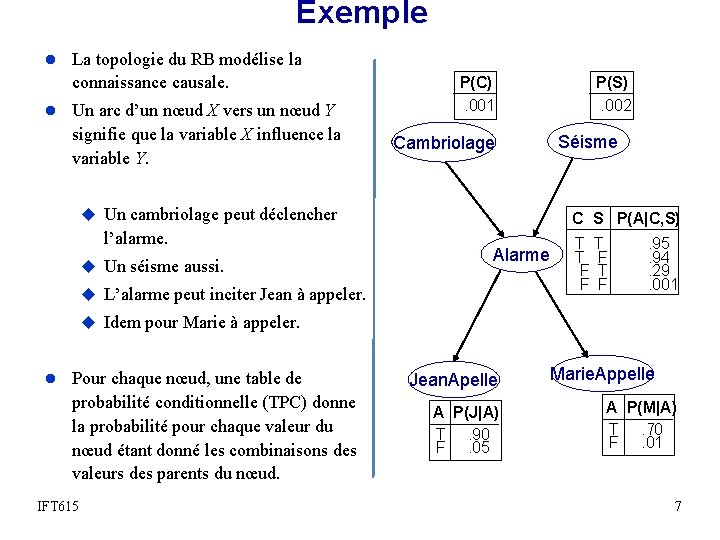
Exemple l La topologie du RB modélise la connaissance causale. l Un arc d’un nœud X vers un nœud Y signifie que la variable X influence la variable Y. P(C). 001 P(S). 002 Séisme Cambriolage u Un cambriolage peut déclencher l’alarme. u Un séisme aussi. C S P(A|C, S) Alarme u L’alarme peut inciter Jean à appeler. T T T F F . 95. 94. 29. 001 u Idem pour Marie à appeler. l Pour chaque nœud, une table de probabilité conditionnelle (TPC) donne la probabilité pour chaque valeur du nœud étant donné les combinaisons des valeurs des parents du nœud. IFT 615 Jean. Apelle A P(J|A) T. 90 F. 05 Marie. Appelle A P(M|A) T. 70 F. 01 7

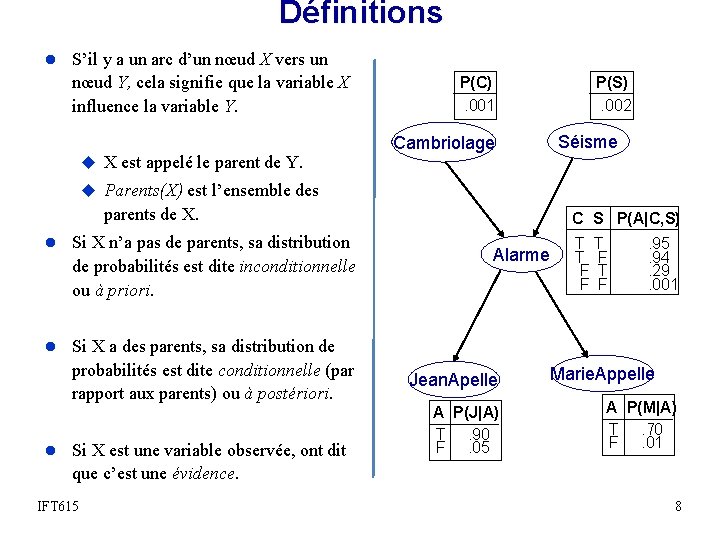
Définitions l S’il y a un arc d’un nœud X vers un nœud Y, cela signifie que la variable X influence la variable Y. u X est appelé le parent de Y. P(C). 001 P(S). 002 Séisme Cambriolage u Parents(X) est l’ensemble des parents de X. l Si X n’a pas de parents, sa distribution de probabilités est dite inconditionnelle ou à priori. C S P(A|C, S) Alarme T T T F F . 95. 94. 29. 001 l Si X a des parents, sa distribution de probabilités est dite conditionnelle (par rapport aux parents) ou à postériori. l Si X est une variable observée, ont dit Jean. Apelle A P(J|A) T. 90 F. 05 Marie. Appelle A P(M|A) T. 70 F. 01 que c’est une évidence. IFT 615 8

Sémantique l Un RB est une façon compacte de représenter des probabilités conjointes. l Par définition, la probabilité conjointe de X 1 et X 2 est la probabilité d’avoir X 1 et X 2 : P(X 1, X 2). l La probabilité conditionnelle de X 1 sachant X 2 est notée P(X 1| X 2). u P(X 1, X 2) = P(X 1 | X 2)P(X 2) l Soit X = {X 1, …, Xn}, l’ensemble des variables d’un RB : P(X , …, X ) = n P (X | Parents(X )) 1 n i=1 i i l En d’autres mots, la distribution conjointe des variables d’un RB est définie comme étant le produit des distributions conditionnelles (locales). u Seules comptent les probabilités de chaque variable connaissant ses parents, pour calculer la distribution conjointe. IFT 615 9

Sémantique l En fait, quelque soit un ensemble de variables X = {X 1, …, Xn}, par définition : P(X 1, …, Xn) = P(Xn | Xn-1, …, X 1)P(Xn-1, …, X 1) = P(Xn | Xn-1, …, X 1) P(Xn-1 | Xn-2, …, X 1) … P(X 2|X 1)P(X 1) = ni = 1 P (Xi | Xi-1, …, X 1) l Pour un RB : P(X 1, …, Xn) =Π in= 1 P (Xi | Parents(Xi)) l Ceci est cohérent avec l’assertion précédente pour autant que Parents(Xi) soit un sous-ensemble de {Xi-1, …, X 1}. l Cette condition est satisfaite en étiquetant les nœuds du RB dans un ordre cohérent avec la relation d’ordre partielle implicite dans la topologie du RB. IFT 615 10

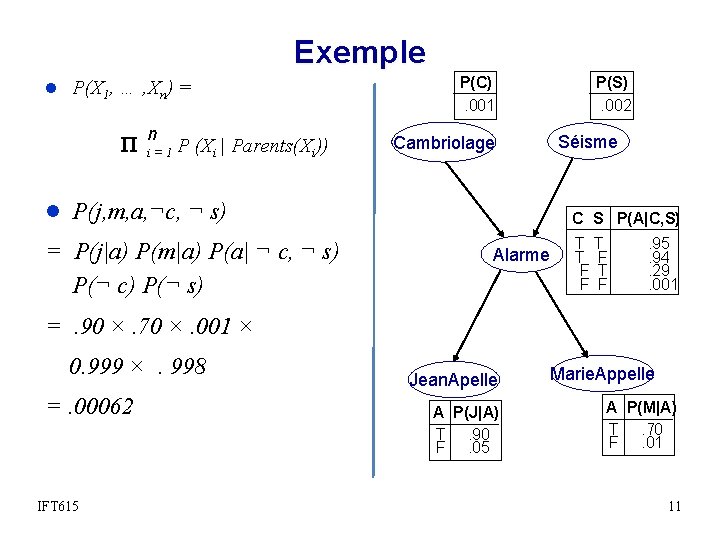
Exemple l P(X 1, … , Xn) = n i=1 P (Xi | Parents(Xi)) P(C). 001 P(S). 002 Séisme Cambriolage l P(j, m, a, ¬c, ¬ s) = P(j|a) P(m|a) P(a| ¬ c, ¬ s) P(¬ c) P(¬ s) C S P(A|C, S) Alarme T T T F F . 95. 94. 29. 001 =. 90 ×. 70 ×. 001 × 0. 999 ×. 998 =. 00062 IFT 615 Jean. Apelle A P(J|A) T. 90 F. 05 Marie. Appelle A P(M|A) T. 70 F. 01 11

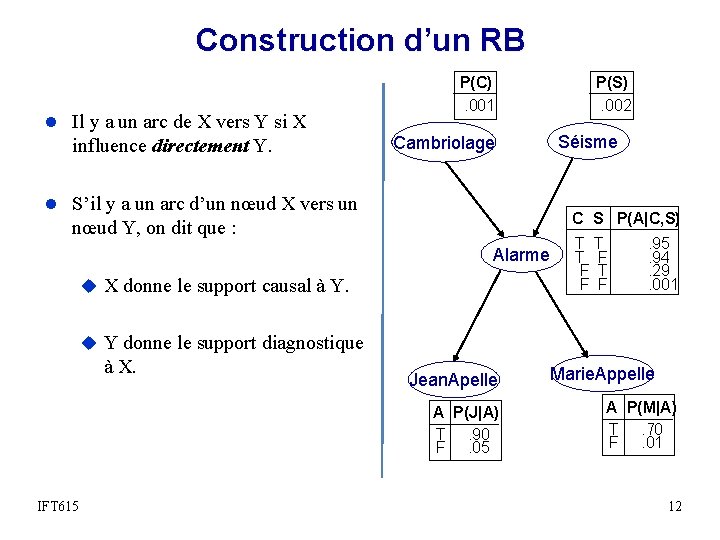
Construction d’un RB l Il y a un arc de X vers Y si X influence directement Y. P(C). 001 P(S). 002 Séisme Cambriolage l S’il y a un arc d’un nœud X vers un C S P(A|C, S) nœud Y, on dit que : Alarme u X donne le support causal à Y. T T T F F . 95. 94. 29. 001 u Y donne le support diagnostique à X. Jean. Apelle A P(J|A) T. 90 F. 05 IFT 615 Marie. Appelle A P(M|A) T. 70 F. 01 12

Construction d’un RB l Pour construire un RB correcte, on s’assure que chaque nœud est indépendant de tous ses prédécesseurs, étant donné ses parents. u En d’autres mots, les parents du nœud Xi devraient être tous les nœuds dans {X 1, …, Xi-1} qui influencent/cause directement Xi l Dans quel ordre ajouter les nœuds au réseau? u Mettre les « causes racines » d’abord, ensuite les nœuds qu’ils influencent directement. IFT 615 13

Construction d’un RB l 1. Choisir un ordre des variables X 1, … , Xn l 2. Pour i = 1 to n: u ajouter Xi au réseau u choisir les parents X 1, … , Xi-1 tel que P (Xi | Parents(Xi)) = P (Xi | X 1, . . . Xi-1) » Ce choix garantit que: • P (X 1, … , Xn) = i n=1 P (Xi | X 1, … , Xi-1) (chain rule) n = i =1 P (Xi | Parents(Xi)) (par construction) IFT 615 14

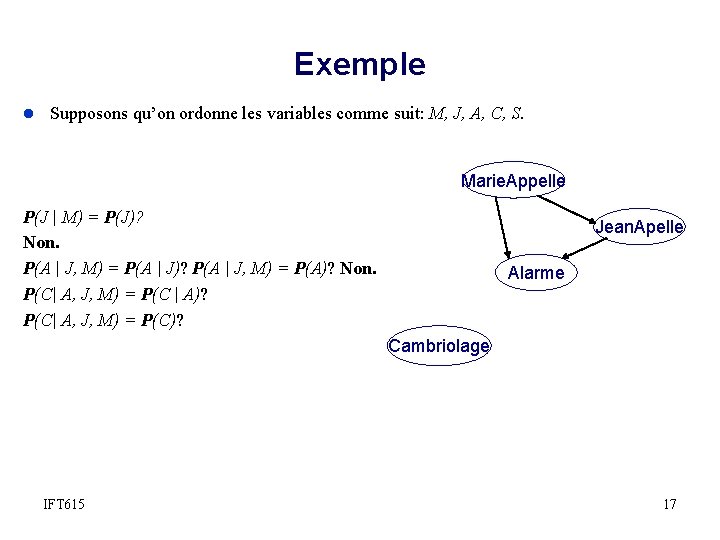
Exemple l Supposons qu’on ordonne les variables comme suit: M, J, A, C, S. Marie. Appelle P(J | M) = P(J)? IFT 615 Jean. Apelle 15

Exemple l Supposons qu’on ordonne les variables comme suit: M, J, A, C, S Marie. Appelle P(J | M) = P(J)? Non. P(A | J, M) = P(A | J)? P(A | J, M) = P(A)? IFT 615 Jean. Apelle Alarme 16

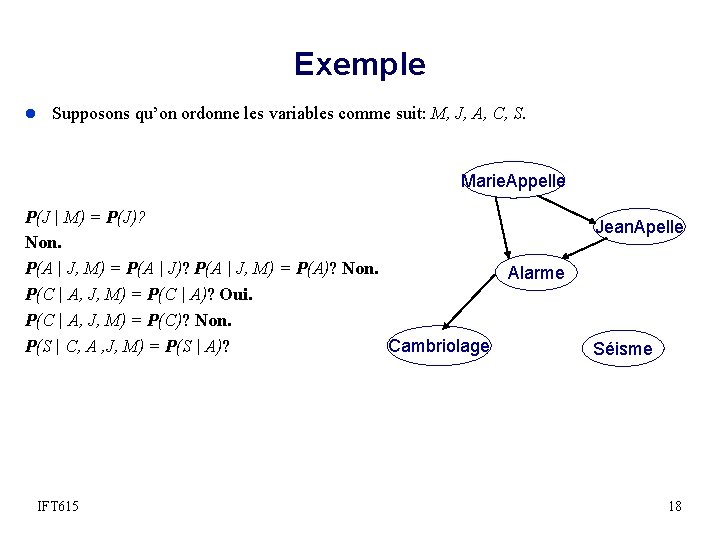
Exemple l Supposons qu’on ordonne les variables comme suit: M, J, A, C, S. Marie. Appelle P(J | M) = P(J)? Non. P(A | J, M) = P(A | J)? P(A | J, M) = P(A)? Non. P(C| A, J, M) = P(C | A)? P(C| A, J, M) = P(C)? Jean. Apelle Alarme Cambriolage IFT 615 17

Exemple l Supposons qu’on ordonne les variables comme suit: M, J, A, C, S. Marie. Appelle P(J | M) = P(J)? Non. P(A | J, M) = P(A | J)? P(A | J, M) = P(A)? Non. Alarme P(C | A, J, M) = P(C | A)? Oui. P(C | A, J, M) = P(C)? Non. P(S | C, A , J, M) = P(S | A)? Cambriolage IFT 615 Jean. Apelle Séisme 18

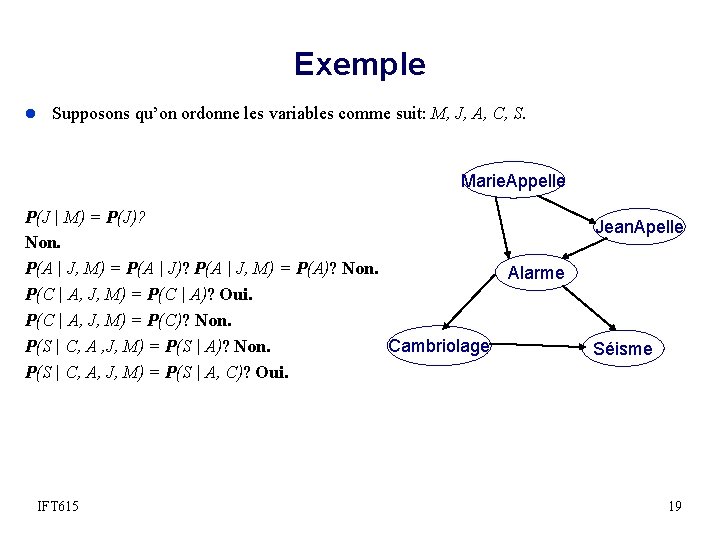
Exemple l Supposons qu’on ordonne les variables comme suit: M, J, A, C, S. Marie. Appelle P(J | M) = P(J)? Non. P(A | J, M) = P(A | J)? P(A | J, M) = P(A)? Non. Alarme P(C | A, J, M) = P(C | A)? Oui. P(C | A, J, M) = P(C)? Non. P(S | C, A , J, M) = P(S | A)? Non. Cambriolage P(S | C, A, J, M) = P(S | A, C)? Oui. IFT 615 Jean. Apelle Séisme 19

Exemple Marie. Appelle Jean. Apelle Alarme Cambriolage Séisme l Déterminer l’indépendance conditionnelle est très difficile dans le sens non causal. u Par exemple, en médecine, des études ont montré que les experts préfèrent donner des probabilités dans le sens causal (pathologie → symptôme) plutôt que dans le sens diagnostique. l Un réseau avec des dépendance diagnostique (effet → cause) est généralement moins compacte. Dans le cas présent: 1 + 2 + 4 = 13 nombres pour représenter les tables de probabilité conditionnelle du réseau au lieu de 10 pour la première version. IFT 615 20

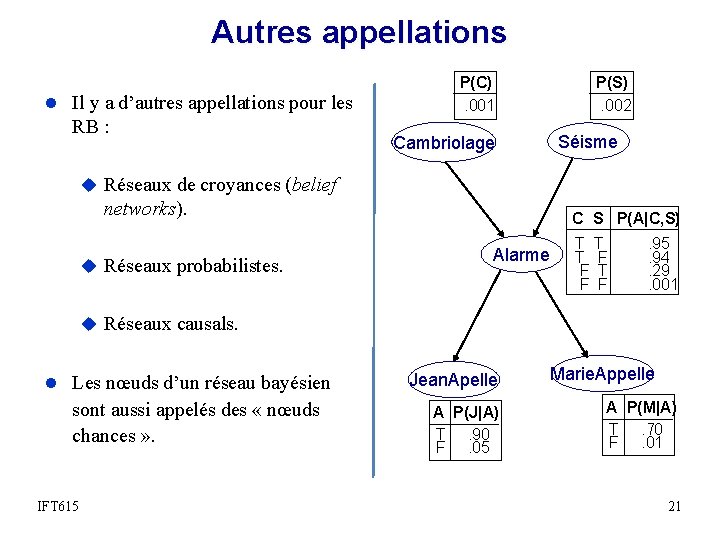
Autres appellations l Il y a d’autres appellations pour les RB : P(C). 001 P(S). 002 Séisme Cambriolage u Réseaux de croyances (belief networks). u Réseaux probabilistes. C S P(A|C, S) Alarme T T T F F . 95. 94. 29. 001 u Réseaux causals. l Les nœuds d’un réseau bayésien sont aussi appelés des « nœuds chances » . IFT 615 Jean. Apelle A P(J|A) T. 90 F. 05 Marie. Appelle A P(M|A) T. 70 F. 01 21

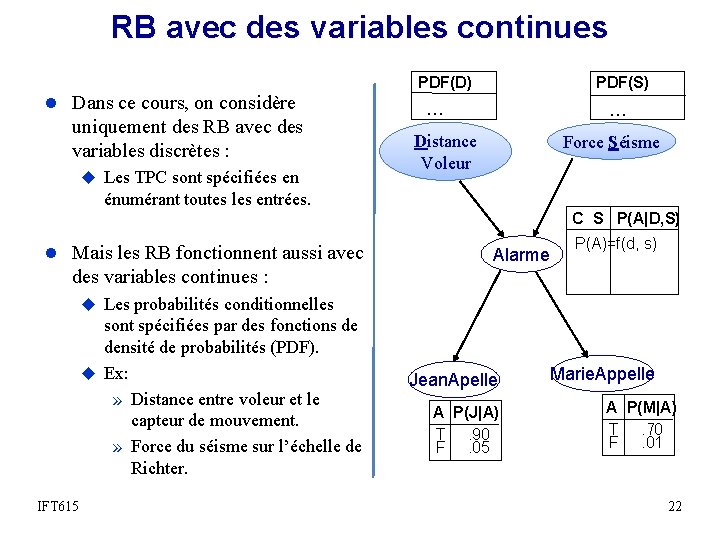
RB avec des variables continues l Dans ce cours, on considère uniquement des RB avec des variables discrètes : u Les TPC sont spécifiées en PDF(D) PDF(S) … … Distance Voleur Force Séisme énumérant toutes les entrées. C S P(A|D, S) l Mais les RB fonctionnent aussi avec Alarme P(A)=f(d, s) des variables continues : u Les probabilités conditionnelles sont spécifiées par des fonctions de densité de probabilités (PDF). u Ex: » Distance entre voleur et le capteur de mouvement. » Force du séisme sur l’échelle de Richter. IFT 615 Jean. Apelle A P(J|A) T. 90 F. 05 Marie. Appelle A P(M|A) T. 70 F. 01 22

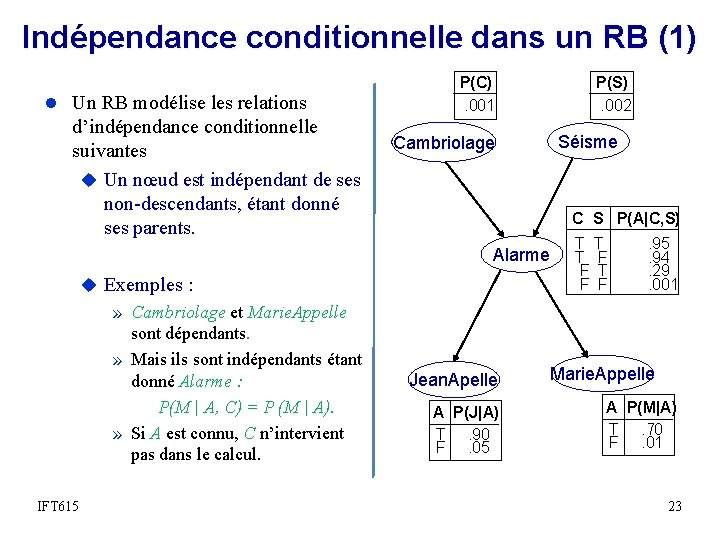
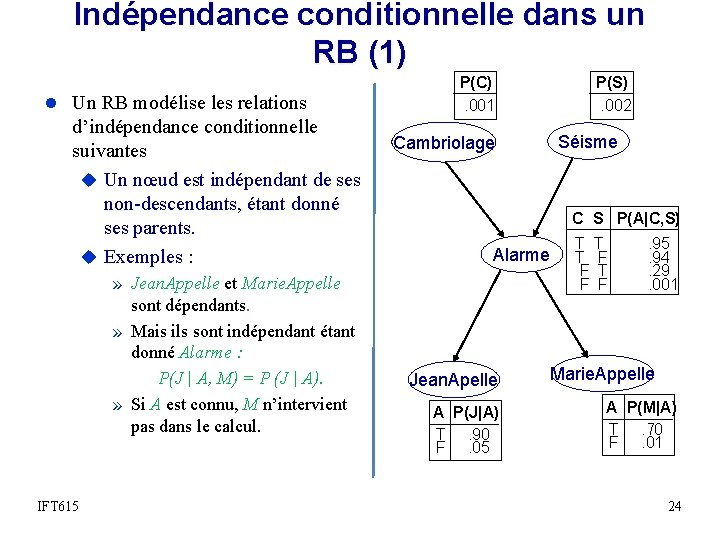
Indépendance conditionnelle dans un RB (1) l Un RB modélise les relations d’indépendance conditionnelle suivantes u Un nœud est indépendant de ses non-descendants, étant donné ses parents. P(C). 001 P(S). 002 Séisme Cambriolage C S P(A|C, S) Alarme u Exemples : » Cambriolage et Marie. Appelle sont dépendants. » Mais ils sont indépendants étant donné Alarme : P(M | A, C) = P (M | A). » Si A est connu, C n’intervient pas dans le calcul. IFT 615 Jean. Apelle A P(J|A) T. 90 F. 05 T T T F F . 95. 94. 29. 001 Marie. Appelle A P(M|A) T. 70 F. 01 23

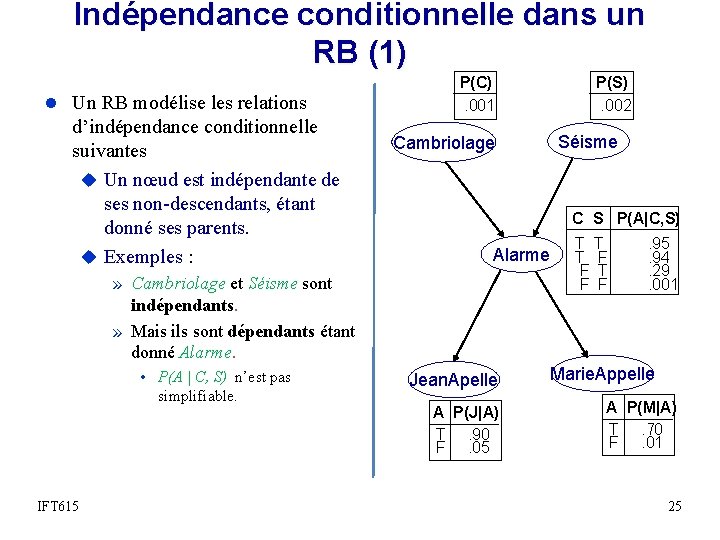
Indépendance conditionnelle dans un RB (1) l Un RB modélise les relations d’indépendance conditionnelle suivantes u Un nœud est indépendant de ses non-descendants, étant donné ses parents. u Exemples : » Jean. Appelle et Marie. Appelle sont dépendants. » Mais ils sont indépendant étant donné Alarme : P(J | A, M) = P (J | A). » Si A est connu, M n’intervient pas dans le calcul. IFT 615 P(C). 001 P(S). 002 Séisme Cambriolage C S P(A|C, S) Alarme Jean. Apelle A P(J|A) T. 90 F. 05 T T T F F . 95. 94. 29. 001 Marie. Appelle A P(M|A) T. 70 F. 01 24

Indépendance conditionnelle dans un RB (1) l Un RB modélise les relations d’indépendance conditionnelle suivantes u Un nœud est indépendante de ses non-descendants, étant donné ses parents. u Exemples : P(C). 001 IFT 615 Séisme Cambriolage C S P(A|C, S) Alarme » Cambriolage et Séisme sont indépendants. » Mais ils sont dépendants étant donné Alarme. • P(A | C, S) n’est pas simplifiable. P(S). 002 Jean. Apelle A P(J|A) T. 90 F. 05 T T T F F . 95. 94. 29. 001 Marie. Appelle A P(M|A) T. 70 F. 01 25

Indépendance conditionnelle dans un RB (2) u Un nœud est conditionnellement indépendant étant donné tous ses parents, enfants et parents de ses enfants (autrement dit étant donné sa couverture de Markov). IFT 615 Couverture de Markov de X 26

Indépendance conditionnelle dans un RB (3) P(C). 001 u D-séparation : critère pour décider si un nœud X est indépendant d’un nœud Y, étant donné un autre nœud Z. P(S). 002 Séisme Cambriolage C S P(A|C, S) u Ce cas est non traité ici. Alarme Jean. Apelle A P(J|A) T. 90 F. 05 IFT 615 T T T F F . 95. 94. 29. 001 Marie. Appelle A P(M|A) T. 70 F. 01 27

Interrogation d’un RB l L’usage principal d’un RB est de calculer la distribution de l l probabilités à postérioris pour un ensemble de variables, étant donné un événement observé. Un événement est une assignation de valeurs à certaines variables d’évidence. Soit u X l’ensemble de variables pour laquelle on fait l’interrogation, u E les variables d’évidences (qu’on peut observer) et u Y les variables cachées (qu’on ne peut pas observer). Une interrogation est du genre P(X|e), où e est une assignation de valeurs à certaines variables dans E. Une interrogation s’appelle aussi faire une inférence. IFT 615 28

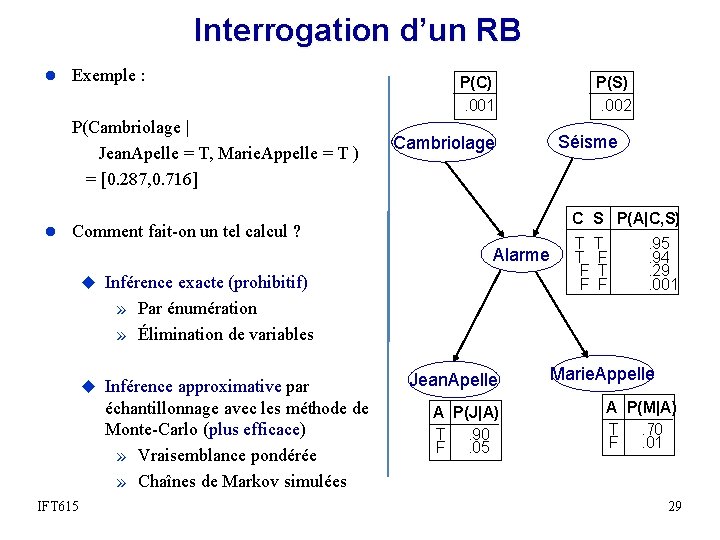
Interrogation d’un RB l Exemple : P(Cambriolage | Jean. Apelle = T, Marie. Appelle = T ) = [0. 287, 0. 716] P(C). 001 P(S). 002 Séisme Cambriolage C S P(A|C, S) l Comment fait-on un tel calcul ? Alarme u Inférence exacte (prohibitif) T T T F F . 95. 94. 29. 001 » Par énumération » Élimination de variables u Inférence approximative par échantillonnage avec les méthode de Monte-Carlo (plus efficace) » Vraisemblance pondérée » Chaînes de Markov simulées IFT 615 Jean. Apelle A P(J|A) T. 90 F. 05 Marie. Appelle A P(M|A) T. 70 F. 01 29

Rappel de notions de base en probabilités l P(X, Z) = P(X|Z)P(Z). l P(Z, X) = P(Z|X)P(X). l On en déduit u P(X|Z) = P(X, Z) / P(Z) u P(X|Z) = P(Z|X)P(X) / P(Z) Règle de Bayes l Si on a une distribution conjointe pour P(Z, Y) on peut calculer la distribution P(Z) par la somme des probabilités pour toutes les valeurs possibles de Y (marginalisation): P(Z) = Σy P(Z, Y = y). l Si on a une distribution conditionnelle P(Z|Y), on peut « conditionner » : P(Z) = Σy P(Z | Y = y)P(Y=y). l P(Z) peut donc être considéré comme un facteur constant, α IFT 615 30

Rappel de notions de base en probabilités l Ceci nous donne u P(X|Z) = α P(X, Z) u α est une constante de normalisation pour s’assurer que la somme des probabilités de la distribution P(X, Z) soit égale à 1. l De manière générale, soit u X, l’ensemble de variables pour laquelle on fait l’interrogation, u E, les variables d’évidences (qu’on peut observer) et u Y, les variables cachées (qu’on ne peut pas observer). u e, les valeurs observées pour les variables dans E. l P(X|E=e) = α P(X, E=e) = Σy P(X, E=e, Y = y) l Noté aussi P(X|e) = α Σy P(X, e, y) IFT 615 31

Inférence par énumération l On a vu que : P(X|e) = α Σy P(X, e, y) l On a vu aussi que selon la sémantique d’un RB P(X 1, … , Xn) = n π i = 1 P (Xi | Parents(Xi)) l Les termes P(X, e, y) peuvent donc s’écrire comme le produit des probabilités conditionnelles du réseau. l En d’autre termes, on peut calculer la réponse à une interrogation P(X|e) sur un RB, simplement en calculant les sommes des produits des probabilités conditionnelles du RB. u Algorithme Figure 14. 9, Page 506 du livre. IFT 615 32

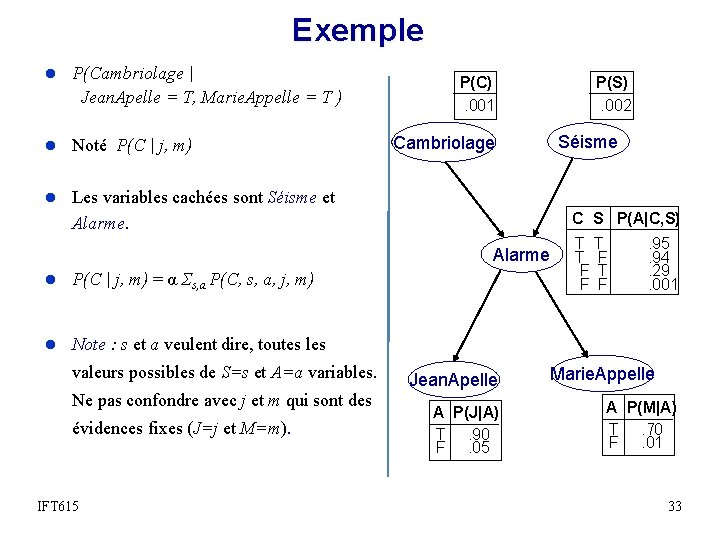
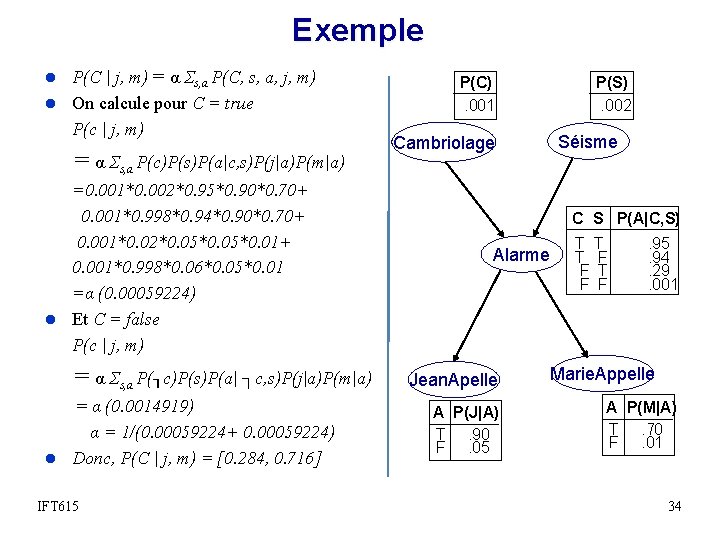
Exemple l P(Cambriolage | Jean. Apelle = T, Marie. Appelle = T ) l Noté P(C | j, m) P(C). 001 P(S). 002 Séisme Cambriolage l Les variables cachées sont Séisme et C S P(A|C, S) Alarme l P(C | j, m) = α Σs, a P(C, s, a, j, m) T T T F F . 95. 94. 29. 001 l Note : s et a veulent dire, toutes les valeurs possibles de S=s et A=a variables. Ne pas confondre avec j et m qui sont des évidences fixes (J=j et M=m). IFT 615 Jean. Apelle A P(J|A) T. 90 F. 05 Marie. Appelle A P(M|A) T. 70 F. 01 33

Exemple l P(C | j, m) = α Σs, a P(C, s, a, j, m) l On calcule pour C = true P(c | j, m) = α Σs, a P(c)P(s)P(a|c, s)P(j|a)P(m|a) =0. 001*0. 002*0. 95*0. 90*0. 70+ 0. 001*0. 998*0. 94*0. 90*0. 70+ 0. 001*0. 02*0. 05*0. 01+ 0. 001*0. 998*0. 06*0. 05*0. 01 =α (0. 00059224) l Et C = false P(c | j, m) = α Σs, a P(┐c)P(s)P(a| ┐c, s)P(j|a)P(m|a) = α (0. 0014919) α = 1/(0. 00059224+ 0. 00059224) l Donc, P(C | j, m) = [0. 284, 0. 716] IFT 615 P(C). 001 P(S). 002 Séisme Cambriolage C S P(A|C, S) Alarme Jean. Apelle A P(J|A) T. 90 F. 05 T T T F F . 95. 94. 29. 001 Marie. Appelle A P(M|A) T. 70 F. 01 34

Inférence par élimination des variables l Même principe que l’inférence par énumération, mais on évite les répétions de calculs déjà faits. u Voir section 14. 4. 2 du livre (3 e édition). IFT 615 35

Inférence approximative l Les méthodes d’inférence exacte sont inefficaces. u Le problème d’inférence est NP-Complet. l Les méthodes d’inférences approximatives sont plus pratiques. u En général, on n’a pas besoin d’un calcul exact des probabilités pour qu’une conclusion tirée d’un RB soit correcte. u Les méthodes approximatives assignent des probabilités aux variables aléatoires en fonction des TPC associées à ces variables. u Ces assignations sont basées sur des simulations stochastiques, plutôt que des observations réelles. l Voir la section 14. 5 dans le livre. IFT 615 36

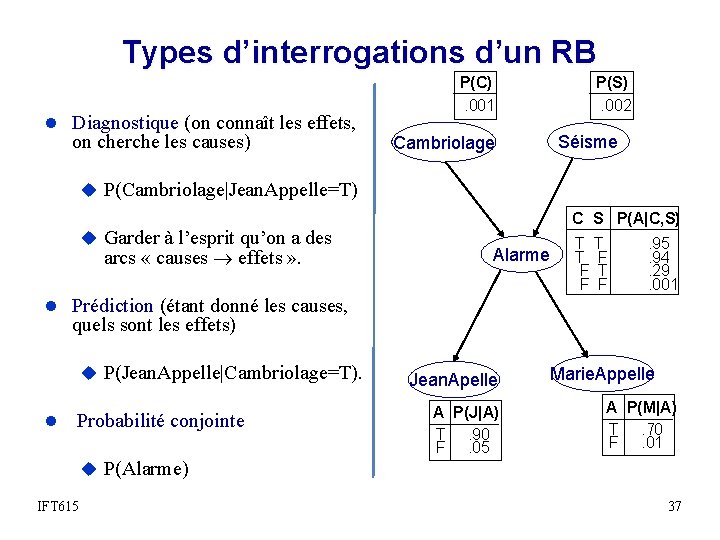
Types d’interrogations d’un RB l Diagnostique (on connaît les effets, on cherche les causes) P(C). 001 P(S). 002 Séisme Cambriolage u P(Cambriolage|Jean. Appelle=T) u Garder à l’esprit qu’on a des arcs « causes effets » . C S P(A|C, S) Alarme T T T F F . 95. 94. 29. 001 l Prédiction (étant donné les causes, quels sont les effets) u P(Jean. Appelle|Cambriolage=T). l Probabilité conjointe Jean. Apelle A P(J|A) T. 90 F. 05 Marie. Appelle A P(M|A) T. 70 F. 01 u P(Alarme) IFT 615 37

Apprentissage d’un RB l La structure d’un RB (le graphe) est le plus souvent spécifiée à l’aide d’un expert. l Dans d’autres applications, la structure est générée automatiquement à partir des données statistiques. u C’est un des problèmes d’apprentissage machine. l Dans d’autres problèmes, on connaît la structure du RB, mais on ne connaît pas les TPC. u Là aussi, on peut les apprendre à partir des données statistiques. u C’est un autre problème d’apprentissage machine. IFT 615 38

Diagrammes d’influence l Un diagramme d’influence (DI) est une extension d’un RB avec des nœuds de décision et des nœuds d’utilité. u Les nœuds habituels d’un RB sont appelés des nœuds chances. u On ajoute : » Des nœuds de décision représentant une prise de décision » Des nœuds d’utilité représentant l’utilité (coût ou degré de désirabilité) des nœuds chances influencés par les actions. l Ainsi on peut modéliser des prises décisions simples u Pour des décisions complexes (séquentielles), les processus de décision de Markov sont généralement préférables. IFT 615 39

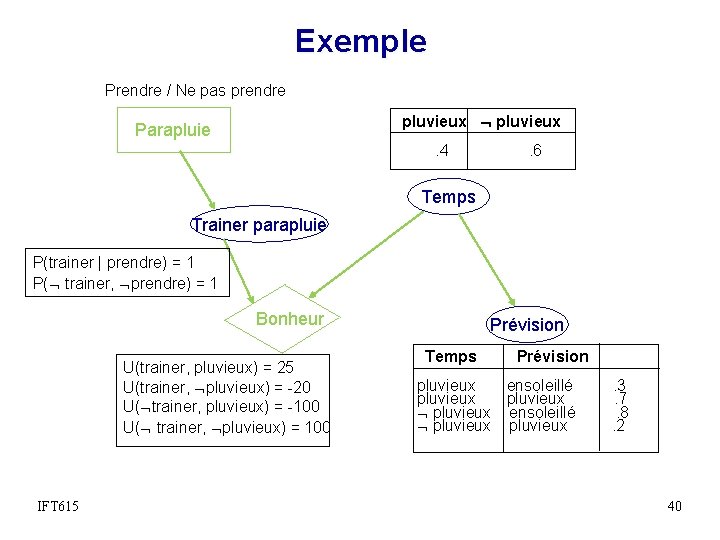
Exemple Prendre / Ne pas prendre pluvieux Parapluie . 4 . 6 Temps Trainer parapluie P(trainer | prendre) = 1 P( trainer, prendre) = 1 Bonheur U(trainer, pluvieux) = 25 U(trainer, pluvieux) = -20 U( trainer, pluvieux) = -100 U( trainer, pluvieux) = 100 IFT 615 Prévision Temps Prévision pluvieux ensoleillé pluvieux ensoleillé pluvieux . 3. 7. 8. 2 40

Évaluation des diagrammes d’influence 1. Mettre à jour les variables d’évidence. 2. Pour chaque valeur possible d’un nœud décision a. Change le nœud décision pour lui donner cette valeur. b. Calcule les probabilités à postérioris des parents des nœuds utilités (en utilisant un algorithme d’inférence standard pour les RB). c. Calcule l’utilité résultante pour l’action. 3. Retourne l’action avec la plus grande utilité IFT 615 41

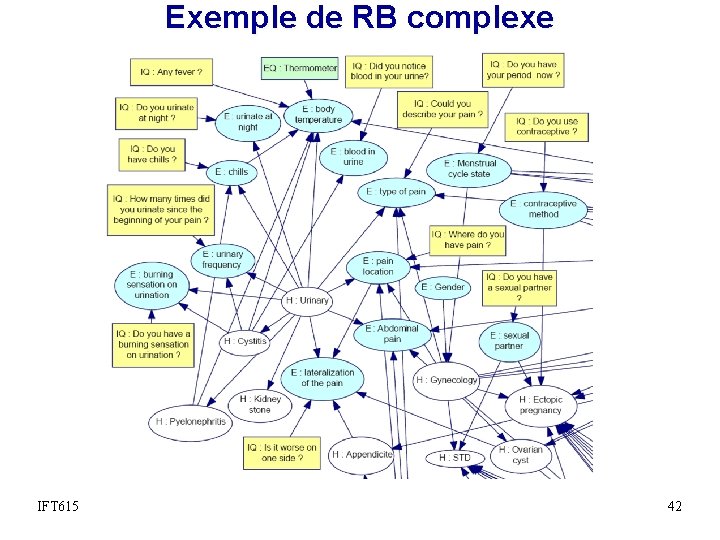
Exemple de RB complexe IFT 615 42

Valeur de l’information l Parfois un agent est amené à prendre des décisions sans posséder toute l’information. l Un aspect important de la prise de décision est de déterminer les questions à poser pour cher de l’information (pour trouver des évidences). l La question la plus pertinente à poser est celle qui apporte le plus d’information : • Les effets d’une action prise suite à la question apporte une différence significative dans le processus de décision. • Ces effets sont très vraisemblables. l Les inférences sur les DI permettent de déterminer les décisions qui apportent le plus d’information. IFT 615 43

AUTRES EXEMPLES D’INFÉRENCE DE RB IFT 615 44

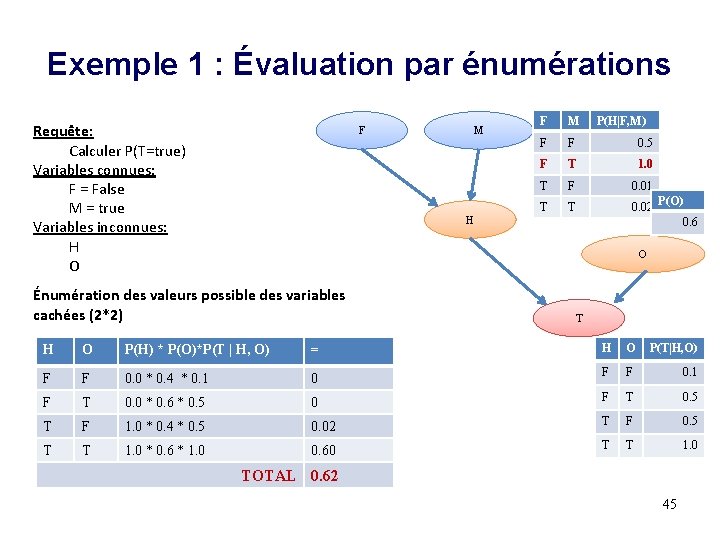
Exemple 1 : Évaluation par énumérations Requête: Calculer P(T=true) Variables connues: F = False M = true Variables inconnues: H O F M H F M P(H|F, M) F F 0. 5 F T 1. 0 T F 0. 01 T T 0. 02 P(O) 0. 6 O Énumération des valeurs possible des variables cachées (2*2) T H O P(H) * P(O)*P(T | H, O) = H O P(T|H, O) F F 0. 0 * 0. 4 * 0. 1 0 F F 0. 1 F T 0. 0 * 0. 6 * 0. 5 0 F T 0. 5 T F 1. 0 * 0. 4 * 0. 5 0. 02 T F 0. 5 T T 1. 0 * 0. 6 * 1. 0 0. 60 T T 1. 0 TOTAL 0. 62 45

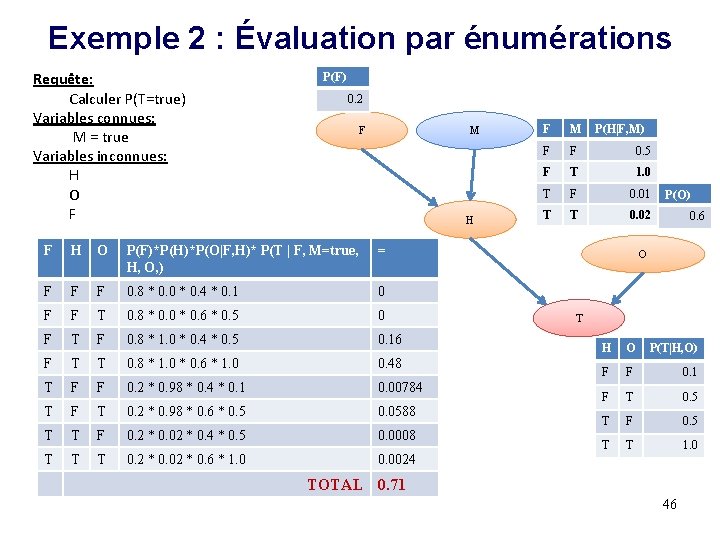
Exemple 2 : Évaluation par énumérations Requête: Calculer P(T=true) Variables connues: M = true Variables inconnues: H O F P(F) 0. 2 F M H F H O P(F)*P(H)*P(O|F, H)* P(T | F, M=true, H, O, ) = F F F 0. 8 * 0. 0 * 0. 4 * 0. 1 0 F F T 0. 8 * 0. 0 * 0. 6 * 0. 5 0 F T F 0. 8 * 1. 0 * 0. 4 * 0. 5 0. 16 F T T 0. 8 * 1. 0 * 0. 6 * 1. 0 0. 48 T F F 0. 2 * 0. 98 * 0. 4 * 0. 1 0. 00784 T F T 0. 2 * 0. 98 * 0. 6 * 0. 5 0. 0588 T T F 0. 2 * 0. 02 * 0. 4 * 0. 5 0. 0008 T T T 0. 2 * 0. 02 * 0. 6 * 1. 0 0. 0024 F M P(H|F, M) F F 0. 5 F T 1. 0 T F 0. 01 T T 0. 02 P(O) 0. 6 O T H O P(T|H, O) F F 0. 1 F T 0. 5 T F 0. 5 T T 1. 0 TOTAL 0. 71 46

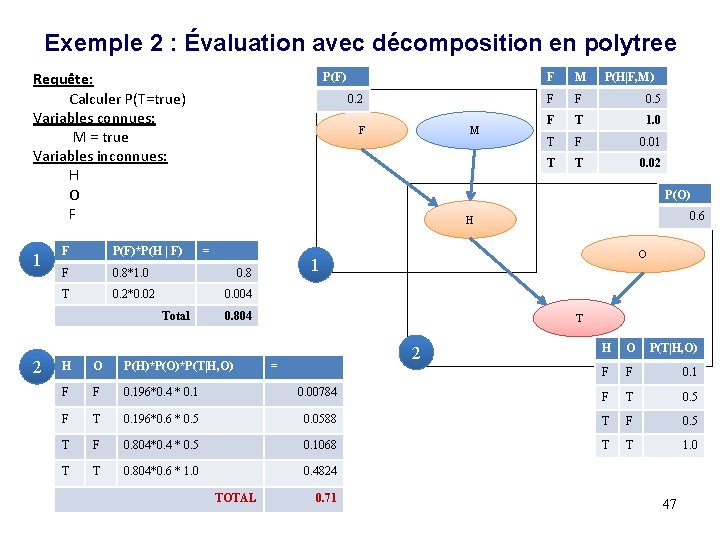
Exemple 2 : Évaluation avec décomposition en polytree Requête: Calculer P(T=true) Variables connues: M = true Variables inconnues: H O F 1 F P(F)*P(H | F) F 0. 8*1. 0 T 0. 2*0. 02 0. 2 F M P(H|F, M) F F 0. 5 F T 1. 0 T F 0. 01 T T 0. 02 P(O) 0. 6 H = O 1 0. 8 0. 004 Total 2 P(F) 0. 804 T 2 O P(T|H, O) F F 0. 1 H O P(H)*P(O)*P(T|H, O) F F 0. 196*0. 4 * 0. 1 0. 00784 F T 0. 5 F T 0. 196*0. 6 * 0. 5 0. 0588 T F 0. 5 T F 0. 804*0. 4 * 0. 5 0. 1068 T T 1. 0 T T 0. 804*0. 6 * 1. 0 0. 4824 TOTAL = H 0. 71 47

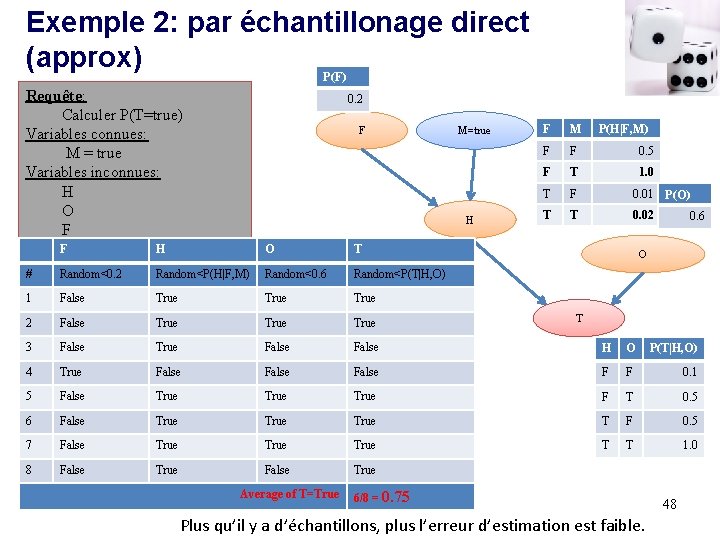
Exemple 2: par échantillonage direct (approx) P(F) Requête: Calculer P(T=true) Variables connues: M = true Variables inconnues: H O F 0. 2 F M=true H F M P(H|F, M) F F 0. 5 F T 1. 0 T F 0. 01 P(O) T T 0. 02 0. 6 F H O T # Random<0. 2 Random<P(H|F, M) Random<0. 6 Random<P(T|H, O) 1 False True 2 False True 3 False True False H O P(T|H, O) 4 True False F F 0. 1 5 False True F T 0. 5 6 False True T F 0. 5 7 False True T T 1. 0 8 False True Average of T=True O T 6/8 = 0. 75 Plus qu’il y a d’échantillons, plus l’erreur d’estimation est faible. 48

Autres appellations l Diagrammes d’influence (influence diagrams). l Réseaux de décision (decision networks) l Diagrammes de pertinence (relevance diagrams) IFT 615 49

Exemples d’applications l Microsoft u Windows : identification des problèmes d’impression. u Office : Microsoft Agent. l NASA u Support au diagnostique en temps réel des pannes du système de propulsion des navettes spatiales. l Médecine u Intellipath : aide au diagnostique des maladies (proposer le diagnostique le plus probable à partir des symptômes; recommander les tests de laboratoires les plus pertinents; recommander les traitements). l AT&T u Détections des fraudes et des mauvais payeurs pour les factures de téléphone. IFT 615 50

Logiciels l Hugin (commercial). l Génie/Smile (domaine publique) IFT 615 51

Résumé - Un RB est un graphe orienté, acyclique, représentant des connaissances causales, et reflétant les dépendances conditionnelles entre des variables. - La topologie du réseau (arcs entres les variables) et les TPC donnent une représentation compacte de la distribution conjointe des probabilités. - Les connaissances du réseau (liens de causalité et probabilités) sont généralement obtenus avec l’aide d’un expert. Ø Pour des applications concrètes, ceci peut être très laborieux. - Un diagramme d’influence est un réseau bayésien avec des nœuds de décision et des nœuds d’utilité. IFT 615 52