IDENTITY BASED ENCRYPTION SECURITY NOTIONS AND NEW IBE

IDENTITY BASED ENCRYPTION SECURITY NOTIONS AND NEW IBE SCHEMES FOR SAKAI KASAHARA KEY CONSTRUCTION N. DENIZ SARIER 1

Introduction • Public Key Encryption follows “encrypt/decrypt” model • A new model of key encapsulation with better flexibility and security proofs 2
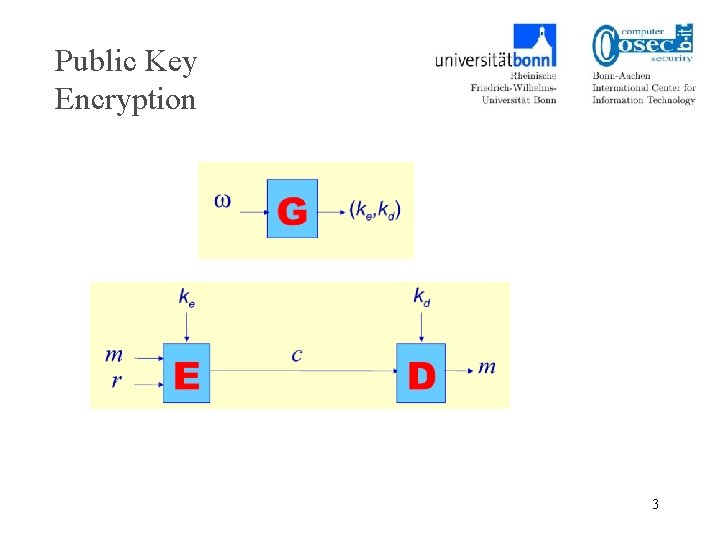
Public Key Encryption 3
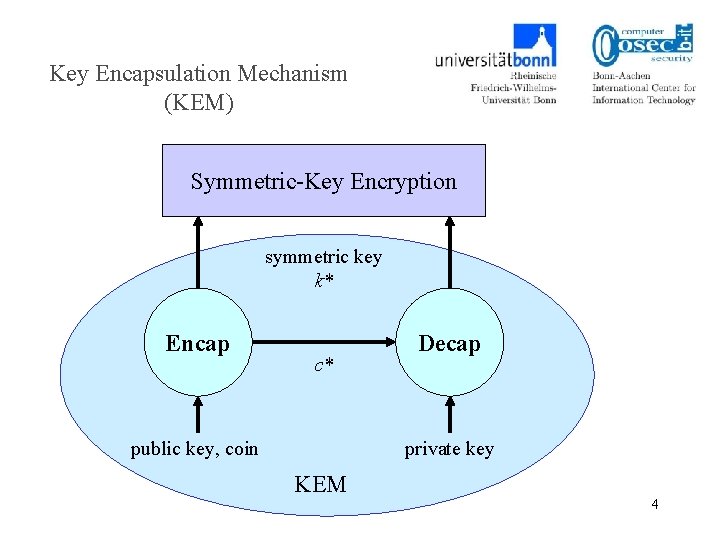
Key Encapsulation Mechanism (KEM) Symmetric-Key Encryption symmetric key k* Encap c* public key, coin Decap private key KEM 4

How to get a Security Proof ? To get a security proof, one needs – Computational problem P, – Security notion, – Cryptosystem – Reduction of the problem P to an attack that breaks the security notion 5

How to get a Security Proof ? Reduction of the problem P to an attack: - Adversary A against the scheme - Reduction uses A to solve P Under the assumption that P is hard, the scheme is unbreakable 6

OUTLINE Today we will discuss • Two new generic constructions • A new computational assumption • Two new identity based encryption schemes 7

A New Generic Construction Theorem: Given any weakly secure Key Encapsulation Mechanism, we construct a Public Key Encryption scheme that is highly secure using two additional secure hash functions 8
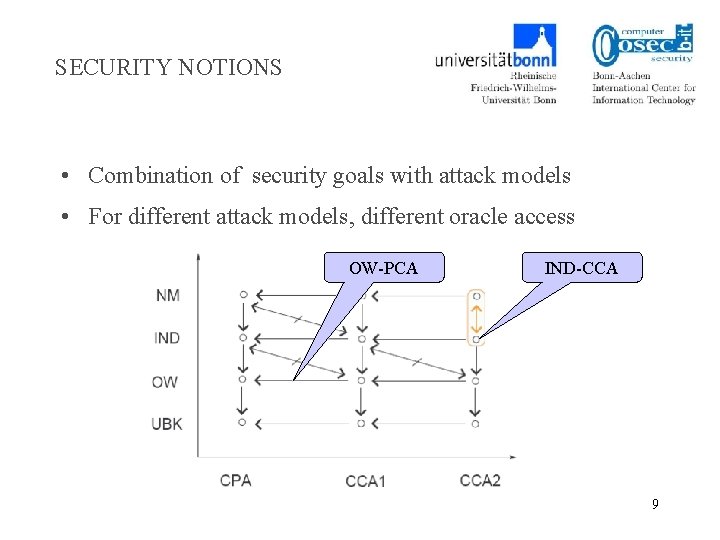
SECURITY NOTIONS • Combination of security goals with attack models • For different attack models, different oracle access OW-PCA IND-CCA 9
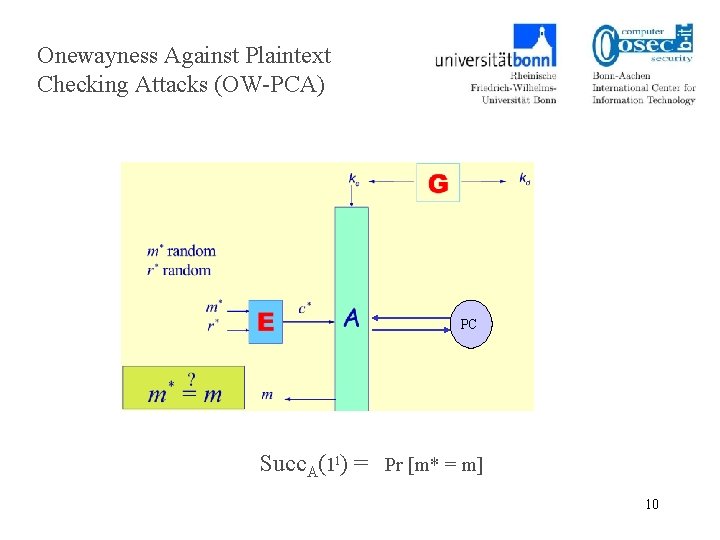
Onewayness Against Plaintext Checking Attacks (OW-PCA) PC PCA Succ. A(1 l) = Pr [m* = m] 10
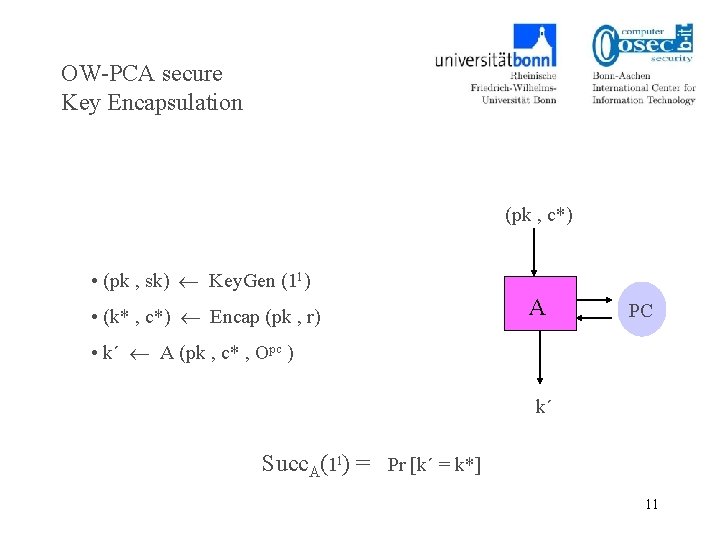
OW-PCA secure Key Encapsulation (pk , c*) • (pk , sk) Key. Gen (1 l ) • (k* , c*) Encap (pk , r) A PC • k´ A (pk , c* , Opc ) k´ Succ. A(1 l) = Pr [k´ = k*] 11
![IND-CCA Adv. A(1 l) = | Pr [b´ = b] – ½ | 12 IND-CCA Adv. A(1 l) = | Pr [b´ = b] – ½ | 12](http://slidetodoc.com/presentation_image/5df12b9b7e25e0aa969a621c13eec43d/image-12.jpg)
IND-CCA Adv. A(1 l) = | Pr [b´ = b] – ½ | 12

A New Generic Construction Theorem: Given any OW-PCA secure Key Encapsulation Mechanism, we construct a Public Key Encryption scheme that is IND-CCA secure using two additional hash functions in random oracle model. 13

Random Oracle Model The basic principle: • The hash function is replaced by a truly random function each time the scheme is used • Throughout the security game, the adversary cannot compute hash values by itself, it must query the oracle embedding the function 14

Random Oracle Model • At start of experiment, H is completely undefined • When H is called with query x for the first time, H selects h uniformly at random over the image set Ĥ and inserts (x , h) in a database H-List • For each query x, H first searches for (x, h) in H-List. If found, h is returned. 15

A New Generic Construction Theorem: Suppose that the hash functions H 2 and H 3 are random oracles. Given any OW-PCA secure Key Encapsulation Mechanism, we construct an IND-CCA secure Public Key Encryption scheme in random oracle model. • A ( , A , q 2 , q 3 , q. D ) • B ( ' , B , q. PC ) ' , B = A + q. PC poly(l) q. PC (q 2 + q 3 + q. D (q 2 + 1)) 16
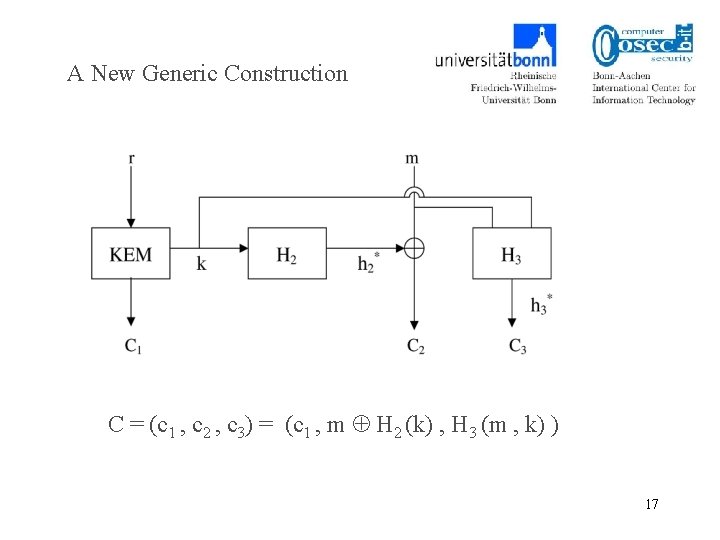
A New Generic Construction C = (c 1 , c 2 , c 3) = (c 1 , m H 2 (k) , H 3 (m , k) ) 17
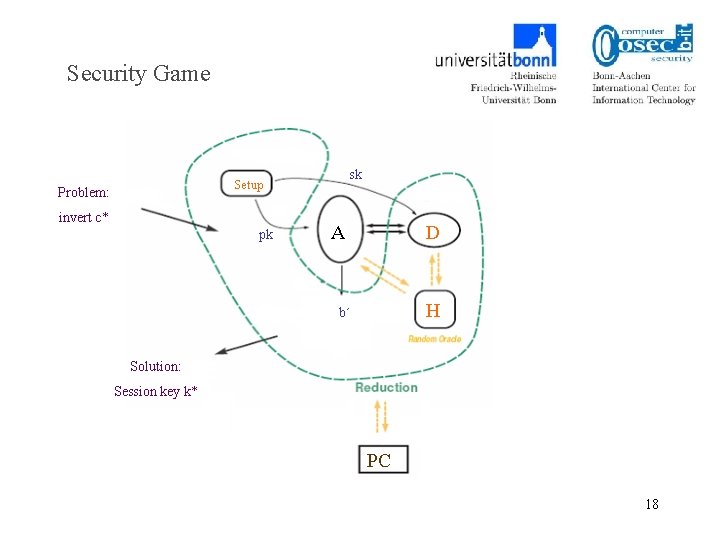
Security Game sk Setup Problem: invert c* pk A D b´ H Solution: Session key k* PC 18

Security Proof C = (c 1 , c 2 , c 3) = (c 1 , m H 2 (k) , H 3 (m , k) ) • (pk , c* , common parameters) • Setup • (pk , common parameters) • H 2 -queries: On each new input k, • If 1 PC (k , c* ) , k* = k , terminate (E 2) • Else , h 2 RANGE (H 2) , (k , h 2) H 2 List. 19

Security Proof C = (c 1 , c 2 , c 3) = (c 1 , m H 2 (k) , H 3 (m , k) ) • H 3 -queries: On each new input (m , k), • If 1 PC(k, c* ) , k* = k , terminate (E 3). • Else, h 3 RANGE(H 3) , (k, m, h 3) H 3 List. • Decryption queries: On each new input (c 1, c 2, c 3) • If (k, m, c 3) H 3 List, return • Elseif m H 2 (k) c 2. , return • Elseif 1 PC (k, c 1) return m, else return . 20

Security Proof C = (c 1 , c 2 , c 3) = (c 1 , m H 2 (k) , H 3 (m , k) ) • Challenge : • A outputs (m 0 , m 1) st. | m 0 | = | m 1 | • B picks h 2* , h 3* where hi * RANGE(Hi ) • B picks {0, 1} and returns C = (c*, m h 2*, h 3* ) to A • B answers A's random oracle and decryption queries as before. • If k* = k , B will return k* , otherwise B fails 21

Simulation of Oracles • Unless k* has been asked to H 2 and H 3 B breaks the OW-PCA of the KEM. • Decryption oracle • C= (c 1, c 2, c 3) rejected if (m, k) H 3 List • A has to guess a right value for h 3 without querying H 3 probability 1/ 2 k 1 ( H 3: {0 , 1}* → {0 , 1}k 1 ) 22

Analysis • Claim: A´s view • Guess. H 3 is A's correctly guessing the output of H 3 Pr [Success. B] = Pr [E 2 V E 3] = | Pr [ ´= ] | Pr [Guess. H 3] – ½ | • From the definition of A | Pr [ ´ = ] – ½ | > Pr [Success. B] > - Pr [Guess. H 3 ] > - q. D / 2 k 1 • ( 2 k = 260 , q. D = 230 Pr [Success. B] ) 1 23
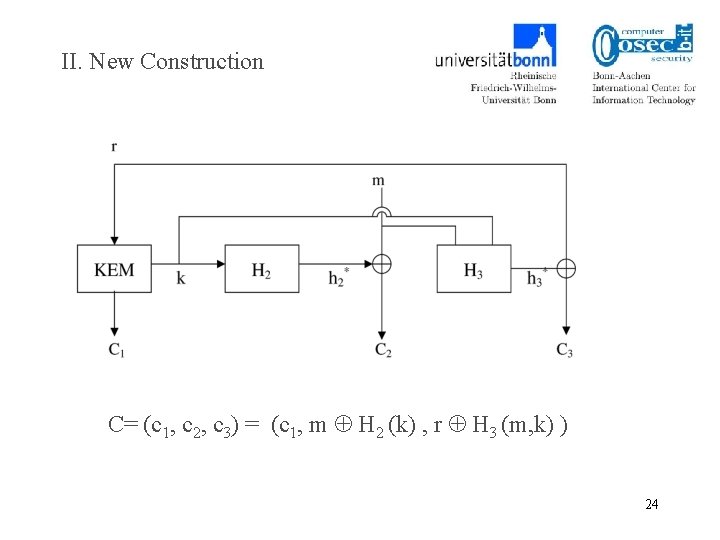
II. New Construction C= (c 1, c 2, c 3) = (c 1, m H 2 (k) , r H 3 (m, k) ) 24

II. New Construction Theorem: • A ( , A , q 2, q 3 , q. D ) • BKEM ( ' , B , q. PC ) • ' , B A + q. PC poly(l) +q. D q 3 is the time to compute KEM(r) = Encap(r , pk) • q. PC (q 2 + q 3 + q. D(q 2+1)) 25

Security Proof C= (c 1, c 2, c 3) = (c 1, m H 2 (k) , r H 3 (m, k) ) • Setup • H 2 –queries • H 3 –queries • Decryption queries: On each new input (c 1, c 2, c 3) • (ki, mi, h 3 i) in H 3 List, ri= h 3 i c 3 • ri check for KEM (ri) = (c 1, ki). If not return • Elseif mi H 2 (ki) c 2. , return , else return mi 26

Analysis • II. Construction can also be proven secure without using the Plaintext Checking oracle. Onewayness of Key encapsulation mechanism At the end of the game, a random entry in H 2 List or H 3 List is choosen The tightness is ' / (q 2 + q 3 ) 27

An Improvement • Additional hash function • C = (c 1 , c 2 , c 3) = (c 1 , m H 2 (k) , r H 3 (m , k) , H 4 (r , m , k , c 1 )) • No check ri , KEM (ri) = (c 1 , k) • B = A + q. PC poly (l) + q. D 28

OUTLINE Today we will discuss • Two new generic constructions • A new computational assumption • Two new identity based encryption schemes 29

Assumptions Diffie-Hellman Inversion (k-DHI): For k Z , x Z*q and P G , given (P, x. P, x 2 P, . . . , xk. P), computing (1/x) P ( for k-BDHI, computing ê(P, P) 1/x ) is hard k-CAA 1’: For k Z and x Z*q , P G , given (P, x. P, (h 1, 1/(x+ h 1)P), …, (hk, 1/(x+ hk) P) ) computing (1/x) P ( for k-BCAA 1’, computing ê(P, P) (1/x) ) is hard. 30
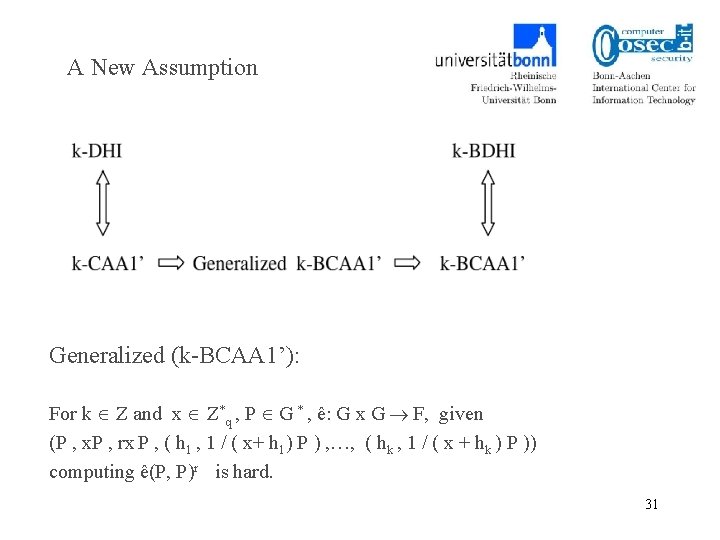
A New Assumption Generalized (k-BCAA 1’): For k Z and x Z*q , P G * , ê: G x G F, given (P , x. P , rx P , ( h 1 , 1 / ( x+ h 1) P ) , …, ( hk , 1 / ( x + hk ) P )) computing ê(P, P)r is hard. 31

OUTLINE Today we will discuss • Two new generic constructions • A new computational assumption • Two new identity based encryption schemes 32
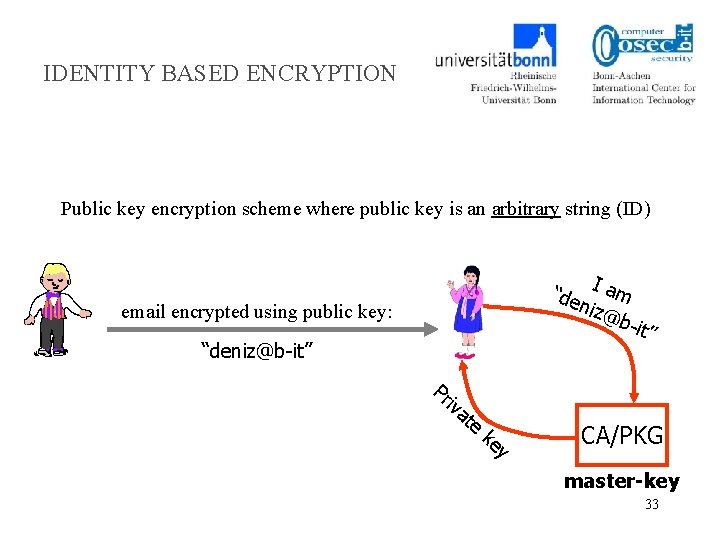
IDENTITY BASED ENCRYPTION Public key encryption scheme where public key is an arbitrary string (ID) I “de am niz@ b-it ” email encrypted using public key: “deniz@b-it” Pr iv at e ke y CA/PKG master-key 33

SAKAI KASAHARA KEY CONSTRUCTION • Setup(l) – a prime q, groups G and F – P G* , ê: G x G F – x∈Zq* , Ppub= x. P –User A’s pk= IDA –User A’s sk = d. A = [1/ (x+H 1 (IDA)) ] P –H 1 is an ordinary hash function (not Map. To. Point) 34

SAKAI KASAHARA´S IBE SCHEME (SK-IBE) • Setup (l) : Four Hash Functions • Encrypt (M, IDA) –σ {0 , 1}n and r = H 3(σ, M) – r. QA = r (x. P + H 1 (IDA)P) –C = < r. QA , σ H 2 (ê (P , P)r) , M H 4(σ) > • Decrypt (C = (U , V , W), d. A) – k´ = ê(d. A , U)) , σ´ = V H 2 (k´) and M´ = W H 4 (σ´) – Integrity check: r´ = H 3 (σ´ , M´) 35
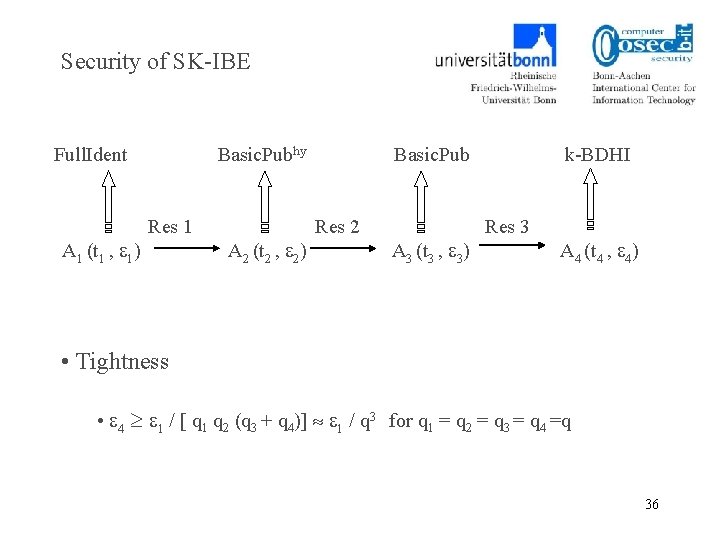
Security of SK-IBE Full. Ident Basic. Pubhy Res 1 A 1 (t 1 , 1) Basic. Pub k-BDHI Res 2 Res 3 A 2 (t 2 , 2) A 3 (t 3 , 3) A 4 (t 4 , 4) • Tightness • 4 1 / [ q 1 q 2 (q 3 + q 4)] 1 / q 3 for q 1 = q 2 = q 3 = q 4 =q 36

A New IBE Scheme SK-IBE 1 • Setup (l): Three Hash functions • Encrypt (m) – r Zq* – r. QA = r(x. P + H 1 (IDA)P) –C = < r. QA , m H 2 (ê (P, P)r) , H 3 (m , (ê (P, P)r) ) > • Decrypt (C = (U , V , W)) – k´ = ê(d. A , U)) , m´ = V H 2 (k´) – Integrity check: H 3 (k´ , m´) = W 37

Security Proof of SK-IBE 1 Theorem: • H 1, H 2 and H 3 are random oracles • ASK-IBE 1 ( A , , q 1, q 2 , q 3 , q. D) • B ( B , ' ‚ q. PC) against GAP-Generalized k-BCAA 1' • ' / q 1 , B = A + q. PC poly(l) • q. PC (q 2 + q 3 + q. D (q 2 + 1)) 38

SK-IBE 2 • Setup (l) • Encrypt (m) –r Zq* –r. QA= r(Ppub + H 1 (IDA)P) –C = <r. QA, m H 2(gr) , r H 3(m, gr) > • Decrypt (C = (U , V , W)) –k´ = ê(d. A , U)) , m´ = V H 2 (k´) –r´ = H 3 (k´ , m´) W –Integrity check: r´QA = U 39

Security Proof of SK-IBE 2 Theorem: • H 1, H 2 and H 3 are random oracles • ASK-IBE 2 ( A , , q 1, q 2 , q 3 , q. D) • B ( B , ' ) solves the Generalized q 1 -BCAA 1' • ' 2 / q 1 (q 2 + q 3 ) , B = A + q. D q 3 is the time to compute ê and multiplication 40

CONCLUSION • Two New Generic Constructions for PKE Setting -IND-CCA secure KEM/DEM -IND-CCA secure PKE • Two New IBE Schemes based on SK Key Construction -SK-IBE 1 GAP Problem, tighter, easier problem -SK-IBE 2 Generalized k-BCAA 1' , less tight, harder problem 41

THANK YOU FOR YOUR ATTENTION 42

A New IBE Scheme SK-IBE 2 • Setup (l) • Extract (IDA) • Encrypt (m) –r Zq* –r. QA= r (Ppub + H 1 (IDA)P) –C = < r. QA , m H 2 (gr) , r H 3 (m , gr) , H 4 (r , m , gr , r. QA) > • Decrypt (C = (U , V , W , Z)) –k´ = ê(d. A , U)) , m´ = V H 2 (k´) –r´ = H 3 (k´ , m´) W – Integrity check: H 4 (r´ , m´ , k´ , r´QA) = Z 43

Hybrid PKE • Hybrid PKE = KEM + DEM • DEM(k) symmetric encryption • DEM • C Encrypt {DEM} (M , k) • M or Decrypt {DEM} (C , k) • Keys of KEM are from the same key space of DEM. 44

IND-CCA • (pk , sk) KGen (1 l) • (m 0 , m 1 , s) A 1 (pk , O) s. t | m 0 | = | m 1 | • b {0 , 1} • c Enc (pk , mb) • b´ A 2 (s , c , O) Adv. A(1 l) = | Pr [b´ = b] – ½ | 45

Key Encapsulation Mechanism (KEM) KEM can be defined by three algorithms: • (pk , sk) KGen (1 l) • (k , c) Encap (pk , r) • k or Decap (sk , c) 46
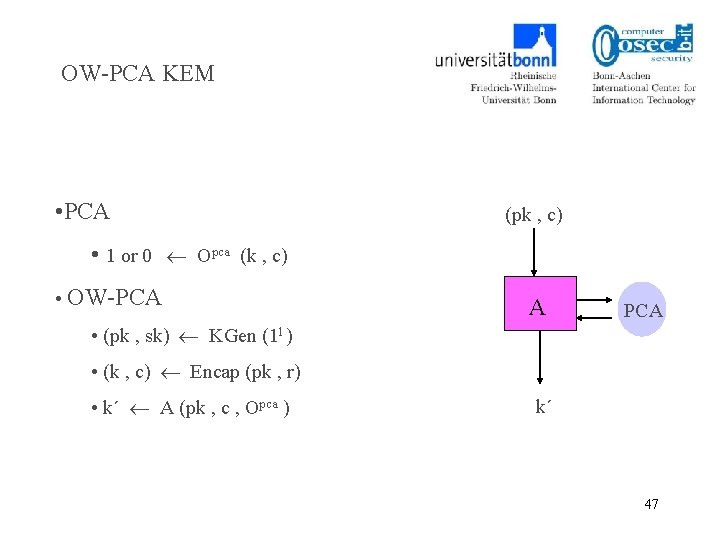
OW-PCA KEM • PCA (pk , c) • 1 or 0 Opca (k , c) • OW-PCA A PCA • (pk , sk) KGen (1 l ) • (k , c) Encap (pk , r) • k´ A (pk , c , Opca ) k´ 47

IDENTITY BASED ENCRYPTION An IBE scheme can be defined by four algorithms: • (param , Mpk and Msk ) Setup (1 l) • di Extract (IDi, , Msk , param) • c C Encrypt (IDi , param , m) • m {0 , 1}n or Decrypt (di , param , c) 48

IND-ID-CCA • (param , Msk) KGen (1 l) • (m 0 , m 1 , s , IDch ) A 1 (param , O 1) s. t | m 0 | = | m 1 | • b {0 , 1} • c Enc (param , IDch , mb ) • b´ A 2 (s , c , O 2) Adv. A(1 l) = | Pr [b´ = b] – ½ | 49

SAKAI KASAHARA´S IBE SCHEME (SK-IBE) • Setup (l) –H 1: {0 , 1}* → Zq* and H 2: F → {0 , 1}n –H 3: {0 , 1}n x {0 , 1}n → Zq* and H 4: {0 , 1}n → {0 , 1}n • Extract (IDA) = d. A • Encrypt (M) –σ {0 , 1}n and r = H 3(σ, M) – r. QA = r (Ppub + H 1 (IDA)P) –C = < r. QA , σ H 2 (gr) , M H 4(σ) > • Decrypt (C = (U , V , W)) – g´ = ê(d. A , U)) , σ´ = V H 2 (g´) and M´ = W H 4 (σ´) – Integrity check: r´ = H 3 (σ´ , M´) 50

Security Proof of SK-IBE 1 Theorem: • H 1, H 2 and H 3 are random oracles • ASK-IBE 1 ( A , , q 1, q 2 , q 3 , q. D) • B ( B , ' ‚ q. PC) against GAP-Generalized k-BCAA 1' • ' / q 1 , B = A + q. PC poly(l) • q. PC (q 2 + q 3 + q. D (q 2 + 1)) 51

Security Proof of SK-IBE 1 • GAP- Generalized k-BCAA 1' • 1 I q 1 ( IND-ID-CCA) , h 0 Zq* • Ppub = x. P - h 0 P • H 1–queries (IDj) • If IDj = IDI , (IDI , h 0 , dj = ) to H 1 List and return h 0 • Else, (IDj , hj + h 0 , dj = 1 / (hj + x)P) to H 1 List and return hj + h 0 52

Security Proof of SK-IBE 1 • Extraction-query (IDi) • If dj , B returns dj • Else, B aborts (E 1) • H 2 –queries (k) • H 3 –queries (m, k) 53

Security Proof of SK-IBE 1 • Decryption query (Ci = (Ui , Vi , Wi) , IDi) • i = I , Ci = ( rix. P , mi H 2 (ê (P , P)ri ) , H 3 (mi , ê(P , P )ri ) • If IDi H 1 List , B queries H 1(IDi) • di = , if (mi , Xi , Wi) H 3 List , reject • If H 2 (Xi) mi Vi , reject • If Xi ê(P , P)ri , reject, else return mi 54

Security Proof of SK-IBE 1 • Challenge ((m 0 , m 1) , IDI)) • If H 1 (IDI) and IDI = IDch and so dch = , B continues, else B aborts (E 4 ) • Else if H 1(IDch) and dch , B aborts (E 5) • Else , (IDch , h 0 , ) to H 1 List and continue • At this stage , H 1 (IDch) = h 0 and dch = • ´ / q 1 55

SK-IBE 2 • Setup (l) • Extract (IDA) • Encrypt (m) –r Zq* –r. QA= r(Ppub + H 1 (IDA)P) –C = <r. QA, m H 2(gr) , r H 3(m, gr) > • Decrypt (C = (U , V , W)) –k´ = ê(d. A , U)) , m´ = V H 2 (k´) –r´ = H 3 (k´ , m´) W –Integrity check: r´QA = U 56

Security Proof of SK-IBE 2 Theorem: • H 1, H 2 and H 3 are random oracles • ASK-IBE 2 ( A , , q 1, q 2 , q 3 , q. D) • B ( B , ' ) solves the q 1 -BDHI • ' 2 / q 1 (q 2 + q 3 ) , B = A + q. D q 3 is the time to compute ê and multiplication 57

Security Proof of SK-IBE 2 • q 1 -BDHI • 1 I q 1 ( IND-ID-CCA), h 0 Zq* , r Zq* • Ppub = x. Q - h 0 Q • H 1–queries (IDj) , • If IDj = IDI , (IDI , h 0 , dj = ) to H 1 List and return h 0 • Else, (IDj , hj + h 0 , dj = 1 / (hj + x)Q) to H 1 List and return hj + h 0 58

Security Proof of SK-IBE 2 • H 2–queries (kj): As a random oracle • H 3–queries (mj , kj): As a random oracle • Decryption queries (C = (Uj , Vj , Wj) , IDI): • Challenge (r. Q , V* , W*) 59

Security Proof of SK-IBE 2 • Guess • Pick a random ki from H 2 List or H 3 List • T = ki (1/r) and return (T / T 0) • ê (P , P) (1/x) = (T / T 0) T = (Q , Q)(1/x) 60

Security Proof of SK-IBE 2 • Analysis • Event E = k (H 2 List H 3 List) • Pr [E ] 2 • Pr [Success. B] 2 / q 1 (q 2 + q 3 ) / q 2 for q 1 = q 2 = q 3 = q 61
- Slides: 61